はじめに
この記事は ちゅらデータ Advent Calendar 2021 7日目の記事です。
6日目の記事はこちら: Google Cloud AutoML Vision Edgeでお手軽エッジモデル構築
本日担当するのは、ちゅらデータで2020年10月からアルバイをしているsoneです。
線形回帰
モデルの構築
入力$x_n$、を基底関数を作用させた $ \boldsymbol{\phi}_n=\left(1,x_n,x_n^2,x_n^3 \right) \in \mathbb{R}^4 $、それに対応する出力を $y_n \in \mathbb{R} $ 、パラメータ $\boldsymbol{w}\in\mathbb{R}^4$ ,ノイズ成分$\epsilon_n\sim\mathcal{N} \left( \epsilon\mid 0,\lambda^{-1} \right)$ を使ってモデル化すると、下のように表すことができます(ただし、$n\in \mathbb{N}$ であり、 $\lambda \in \mathbb{R} _+ $ は1次元ガウス分布の既知の精度パラメータとします)。
\boldsymbol{\Phi}= \left(
\begin{array}{c}
\boldsymbol{\phi}_1 \\
\vdots\\
\boldsymbol{\phi}_N
\end{array}
\right)
\\
y_n = \boldsymbol{w}^{\top} \boldsymbol\Phi+\epsilon_n \qquad
(1.1)
(1.1)を確率分布として定式化すると、
p \left( y_n\mid\boldsymbol\Phi,\boldsymbol{w} \right)=\mathcal{N} \left( y_n\mid\boldsymbol{w}^{\top} \boldsymbol\Phi,\lambda^{-1} \right)
今回はパラメータ $\boldsymbol{w}$ を観測データから学習しておいたので事前分布を $p \left(\boldsymbol{w} \right)=\mathcal{N} \left(\boldsymbol{w}\mid\boldsymbol{m},\boldsymbol{\Lambda}^{-1} \right)$ と設定します(ただし、$\boldsymbol{m}\in \mathbb{R}^4$ は平均パラメータ,正定値行列
$ \boldsymbol{\Lambda} \in M_4 \left( \mathbb{R} \right)$ は精度パラメータ)。これらのパラメータはハイパーパラメータなので事前に準備をしておきます。
事後分布と予測分布の計算
$\boldsymbol{X}= \left( \boldsymbol{x_1},\cdots,\boldsymbol{x_N} \right),\boldsymbol{Y}= \left(y_1,\cdots,y_N \right) $
事後分布は $p \left(\boldsymbol{w}\mid\boldsymbol{Y},\boldsymbol{X} \right)=\mathcal{N} \left(\boldsymbol{w}\mid\boldsymbol{m}_N,\boldsymbol{S}_N \right)$ のようになります。
\boldsymbol{m}_N=\boldsymbol{S}_N \left(\boldsymbol{\Lambda}^{-1}\boldsymbol{m}+ \lambda\boldsymbol{\Phi}^{\top}\boldsymbol{Y} \right) \\
\boldsymbol{S}_N^{-1}=\boldsymbol{\Lambda}^{-1}+\lambda\boldsymbol{\Phi}^{\top} \boldsymbol{\Phi}
あたらしい値 $ x_* $ が与えられたときに $ y_* $ を予測します。
予測分布は
p \left( y_* |x_* \right) = \mathcal{N} \left( y_* \mid \mu_* ,\lambda_* ^{-1} \right) \\
\mu_* = \boldsymbol{m}_N^{\top}\phi \left( x \right)\\
\lambda_* ^{-1}=\lambda^{-1}+\phi \left( x \right) ^{\top}\boldsymbol{S}_N\phi \left( x \right)
になります。
pythonで実行してみる
# ライブラリの準備
import numpy as np
import random
import matplotlib.pyplot as plt
from scipy import stats
from scipy.stats import norm
from scipy.stats import uniform
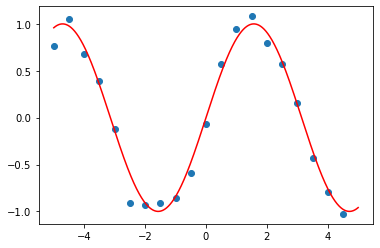
学習用のデータを作成、今回はsin関数
x=np.arange(-5, 5, 0.5).astype(np.float32)
x_=np.arange(-5, 5, 0.001).astype(np.float32)
noise=[]
lamb=10 #ノイズの精度パラメータ
[noise.append(norm.rvs(0,1/lamb)) for _ in range(len(x))]
d=4 #多項式の乗数
y=np.sin(x)
y+=np.array(noise).astype(np.float32)
fig, ax = plt.subplots()
ax.scatter(x, y)
y_t=np.sin(x_)
ax.plot(x_,y_t,c='r')
plt.show()
モデルを構築する
基底関数は3次元の多項式 $y_n=w_{0,n}+w_{1,n}x_n+w_{2,n} x_n ^2+w_{3,n} x_n ^3$ を使って学習させていきます。
基底関数を作成
def phi(x, degree):
return [np.power(x, d) for d in np.arange(0, degree+1)]
ハイパーパラメータの設定
X = np.array(list(map(lambda x_n:phi(x_n, d), x))) #観測データ
S = (1./2)* np.eye(X.shape[1])#事前分布の分散
M =np.zeros(S.shape[0])#事前分布の平均
事後分布
\boldsymbol{m}_N=\boldsymbol{S}_N(\boldsymbol{\Lambda}^{-1}\boldsymbol{m}+ \lambda\boldsymbol{\Phi}^{\top}\boldsymbol{Y}) \\
\boldsymbol{S}_N^{-1}=\boldsymbol{\Lambda}^{-1}+\lambda\boldsymbol{\Phi}^{\top}\boldsymbol{\Phi}
SN_1=lamb * np.dot(X.T, X)+np.linalg.inv(S) #事後分布の精度パラメータ
MN=np.dot(np.linalg.inv(SN_1),(np.dot(S,M)+lamb*np.dot(X.T,y))) #事後分布の平均
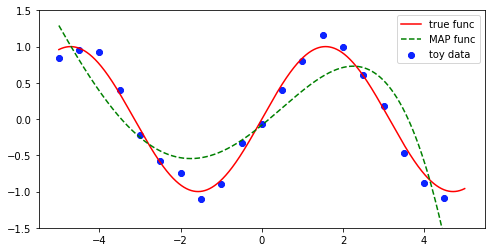
MAP推定
w_MAP = MN
y_MAP = np.array([np.dot(w_MAP, phi(x_n, d)) for x_n in x_])
fig = plt.figure(figsize=(8, 4))
ax = fig.subplots(1,1)
ax.scatter(x, y, color='blue', label='toy data')
ax.plot(x_, y_t, color='red', label='true func')
ax.plot(x_,y_MAP, '--', color='green', label='MAP func')
ax.set_ylim(-1.5,1.5)
ax.legend()
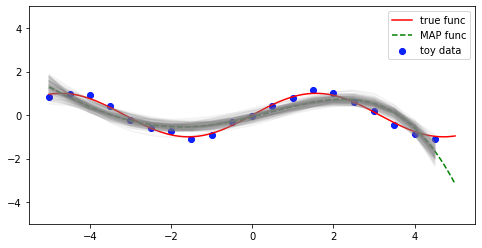
$\boldsymbol{w_t} \sim \mathcal{N}(\boldsymbol{w}|\boldsymbol{m}_N,\boldsymbol{S}_N)$事後分布からランダムに100個重みを取ってきて図示してみます。
sample_post_ws = stats.multivariate_normal.rvs(mean=MN, cov=np.linalg.inv(SN_1), size=100) #事後分布から重みをランダムに取ってくる
fig = plt.figure(figsize=(8, 4))
ax = fig.subplots(1,1)
ax.scatter(x, y, color='blue', label='toy data')
ax.plot(x_, y_t, color='red', label='true func')
ax.plot(x_, y_MAP, '--', color='green', label='MAP func')
for ws in sample_post_ws:
y_sample_post = np.array([np.dot(ws, phi(x_n, d)) for x_n in x])
ax.plot(x, y_sample_post, color='gray', alpha=0.1)
ax.set_ylim(-5, 5)
ax.legend()
予測
\mu_* = \boldsymbol{m}_N^{\top}\phi(x)\\
\lambda_* ^{-1}=\lambda^{-1}+\phi(x)^{\top}\boldsymbol{S}_N\phi(x)
def mu_pred(x): #予測分布の平均
mu = np.dot(MN.T, phi(x, d))
return mu
def var_pred(x): #予測分布の分散
feature = np.array(phi(x, d))
var = 1/lamb + np.dot(np.dot(feature, np.linalg.inv(SN_1)), feature)
return var
新規でデータを作成して、予測分布の平均と分散を求めます
x_inf = np.linspace(-5, 5, 10) #-5から5の間のxを取ってくる
mu_preds = [mu_pred(x) for x in x_inf] #平均の計算
var_preds = [var_pred(x) for x in x_inf] #分散の計算
# 3-sigma範囲
sig_upper = mu_preds + np.sqrt(var_preds) * 3.0
sig_lower = mu_preds - np.sqrt(var_preds) * 3.0
fig = plt.figure(figsize=(8, 4))
ax = fig.subplots(1,1)
ax.scatter(x, y, color='blue', label='toy data')
ax.plot(x_, y_t, color='red', label='true func')
ax.plot(x_, y_MAP, '--', color='green', label='MAP func')
ax.scatter(x_inf, mu_preds, color='black', label='inference')
ax.fill_between(x_inf, sig_lower, sig_upper, color='gray', alpha=0.15)
ax.set_ylim(-5, 5)
ax.legend()