1. 二値分類タスクにおける評価指標
二値分類タスクにおける評価指標には、予測値を連続値のまま評価するものと、0/1に割り当てた上で評価するもの(混同行列に基づくもの)の2通りがあります。
機械学習モデルの全体的な予測性能を評価する場合は、LogLossやAUCなどの前者の指標が使われることが多いですが、予測値に基づくアクションが二値になる場合(例:広告を配信する/しない、病気と診断する/しない)などでは、後者で評価を行いたいこともあるでしょう。
後者の混同行列に基づく評価指標にはいくつかありますが、本記事の主旨はインバランスデータにおけるそれらの挙動を比較、考察することです。
初めに断っておきますが、「こういう場合にはこの指標を使うべき」とか、そういった結論らしい結論は、すみませんがありません。豆知識程度のものだと思ってください。また、本記事で述べる考察は、極めて単純な人工データに基づくものですので、あらゆるデータに一般化できるとは限らない、という点にも注意してください。
まずは、本記事で扱う評価指標を簡単に説明していきますが、それに先立って混同行列を掲載しておきます。(正例を1、負例を0とします。)
| 予測値 | |||
|---|---|---|---|
| 0 | 1 | ||
| 実測値 | 0 | True Negative (TN) | False Positive (FP) |
| 1 | False Negative (FN) | True Positive (TP) | |
Accuracy
Accuracyは、二値分類における最も単純な指標で、全データの内正しく0/1を予測できたものの割合です。
$$\text{Accuracy} = \frac{TP + TN}{TP+FN + TN+FP}$$
もはや常識ではありますが、正例と負例の比率が極端に偏っている場合、Accuracyは無意味な予測に対しても大きな値を取り得るので注意が必要です。例えば、正例が1%しか存在しない不均衡データに対し、全てを負例と予測した場合、Accuracyは0.99となります。
このように、不均衡データに対してAccuracyを用いるのは混乱の元になりますし、モデル改善の指針としても不適切なので、避けるべきです。
Balanced Accuracy
Balanced Accuracyは、正例と負例でそれぞれ正答率を出した後で、それらの平均を取る指標です。つまり、真陽性率と真陰性率の平均値です。
$$\text{Balanced Accuracy} = \frac{1}{2} \left( \frac{TP}{TP+FN} + \frac{TN}{TN+FP} \right)$$
正例と負例の比率が偏った場合でも、正例全体と負例全体が同じ重みで評価されるため、Accuracyで述べたような問題は生じません。
予測能力を持たない予測値(全て正例/全て負例/ランダム予測)に対して、Balanced Accuracyは0.5となります。シンプルな考え方で、それゆえイメージもしやすいですが、以後の検証で示すように、インバランスデータでは少数クラスの検出にかなり重きを置いた指標になります。
また、インターネット上を検索しても 、他の指標に比べてヒットが少なく、あまり使われていないのかもしれません。(その点については、後に考察しています。)
F1スコア
F1スコアは、「1と予測したものの内、真に1であった割合」であるPrecisionと、「真に1であるものの内、1と予測できたものの割合」であるRecallを用いて、次式で表されます。
$$
F_1 = 2 \cdot \frac{\text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}}
\left( \text{Precision}= \frac{TP}{TP+FP}, \text{Recall}= \frac{TP}{TP+FN} \right)
$$
これは、PrecisionとRecallの調和平均になっています。(少し調べたところ、共通の分子を持つ比の平均を計算する際は、算術平均ではなく調和平均を用いるのが適切である、という説明があり、個人的には一番しっくりきています。)
PrecisionとRecallの定義から考えると、F1スコアは正例に注目した指標であるといえます。したがって、「0/1の分類性能を測る」というよりは、「1を正確に検出する性能を測る」と言った方が、より近いイメージかもしれません。
このような性質から、インバランスデータ専用の指標と言えますが、以後の検証で示すように、偏りが大きくなるにつれて、大きい値が出にくくなります。
ラベルの0/1を入れ替えると値が変わりますが、多数派のクラスを1と割り当ててしまうと、F1スコアはAccuracy同様、役に立たない指標となってしまいます。その点については以下のリンクで詳しく述べられていますが、割り当てを気を付ければいいだけの話なので、個人的には大した問題ではないと思います。
Matthews相関係数
Matthews相関係数は、真値と予測値の相関を測る指標です。混同行列の要素を使って書くと、次式のようになります。
$$ MCC = \frac{TP \cdot TN - FP \cdot FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}} $$
この式からは直感的なイメージが困難ですが、これは真値と予測値(二値)に対して通常の(ピアソンの積率)相関係数を計算した結果と一致します。そう考えると、むしろ比較的イメージしやすい指標になります。
両者の一致については過去に記事を書いたのですが、実はそれよりも以前にguchio3氏のブログで同じことが書かれているのを後から見つけました。その他の性質にも触れられているので、こちらの方が有益だと思います。
- guchio3氏のブログ記事:Matthews Correlation Coefficient (MCC) について勉強した
- 私の過去記事:マシューズ相関係数とピアソンの積率相関係数の一致を示す計算過程
Matthews相関係数は、均衡/不均衡関わらず用いることができる指標ではありますが、偏りが大きいと、F1スコアと同様、直感よりも低めの値が出る傾向にあります。
2. 実験による比較と考察
2.1. 不均衡でない場合(正例:負例 = 50000:50000)
まずは、正例と負例が均等な二値分類タスクを考えます。モデルを学習した結果、正例と負例が50000ずつ存在するテストデータに対して、ROC-AUCが約0.9となる予測値が得られた、というケースを、下記のコードでシミュレーションします。
n_negative = 50000
n_positive = 50000
sigma = 1 / 1.795
np.random.seed(1)
y_train = np.concatenate([np.zeros(n_negative), np.ones(n_positive)]).astype(int)
X_train = (y_train + sigma * np.random.randn(n_negative + n_positive)).reshape(-1, 1)
model = LogisticRegression()
model.fit(X_train, y_train)
np.random.seed(0)
y_test = np.concatenate([np.zeros(n_negative), np.ones(n_positive)]).astype(int)
X_test = (y_test + sigma * np.random.randn(n_negative + n_positive)).reshape(-1, 1)
preds = model.predict_proba(X_test)[:, 1]
ターゲットである0/1に正規乱数を乗せることにより特徴量を1つだけ生成し、これを入力としたロジスティック回帰により予測値を生成しています。(二値変数に正規乱数を乗せると言うと気持ち悪さを感じるかもしれませんが、2群間で平均の異なる正規分布に従う量が観測できるという状況を考えれば、極めて自然です。)
ただ、これはあくまで予測値の値をそれっぽいものにするための処理であって、今回の検証においては、学習データの量、特徴量の数や性質、学習手法などの条件は本質的に関係がありません。なので、他の適当なもので置き換えて考えてください。
上記コードのsigmaを調整して、ROC-AUCが0.9になるように予測値を生成しました。予測値のヒストグラムと、ROC曲線およびPR曲線を描画すると、下図のようになります。
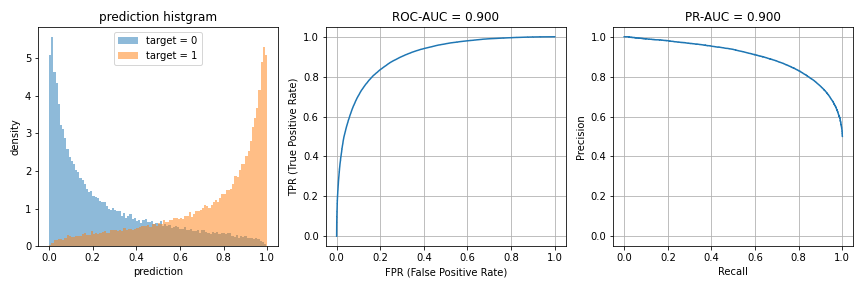
PR曲線は、インバランスデータでROC曲線の代わりに利用が推奨されることがあるため、後の比較のために描画しています。PR-AUCはROC-AUCに比べ、上位の予測値を重視する評価指標であることが、他の方の記事で述べられています。
ちなみに、本題とは直接関係無いですが、ROC曲線とAUCについては過去に以下の記事を書いていますので、よければご参照ください。
このとき、予測値のどこかに閾値を設けて0/1を割り当てれば、混同行列に基づく評価指標で評価を行うことができます。例えば、閾値0.5で0/1を分割すると、以下のような混同行列と評価指標の値が得られます。
| 予測値 | |||
|---|---|---|---|
| 0 | 1 | ||
| 実測値 | 0 | 40967 | 9033 |
| 1 | 9138 | 40862 | |
次に、閾値を動かしたときの各指標の変化を見てみましょう。
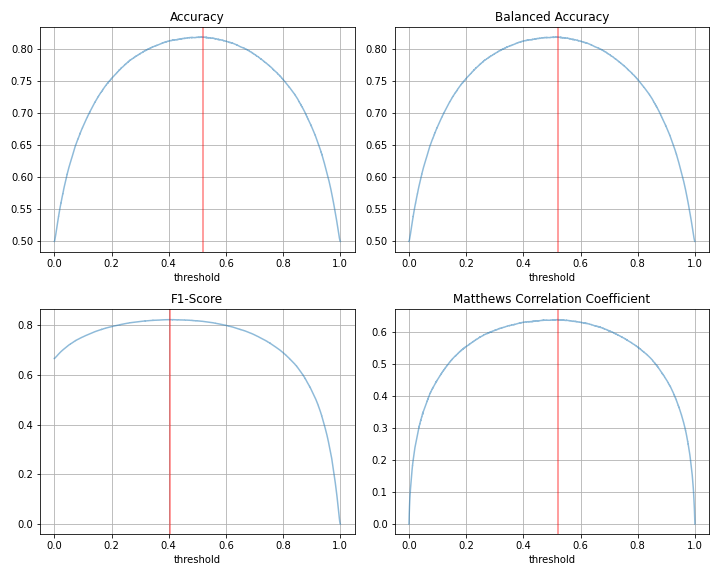
上図では0/1を分割する閾値を横軸に取っていますが、何%のデータを1と予測するか、を横軸にとると下図のようになります。
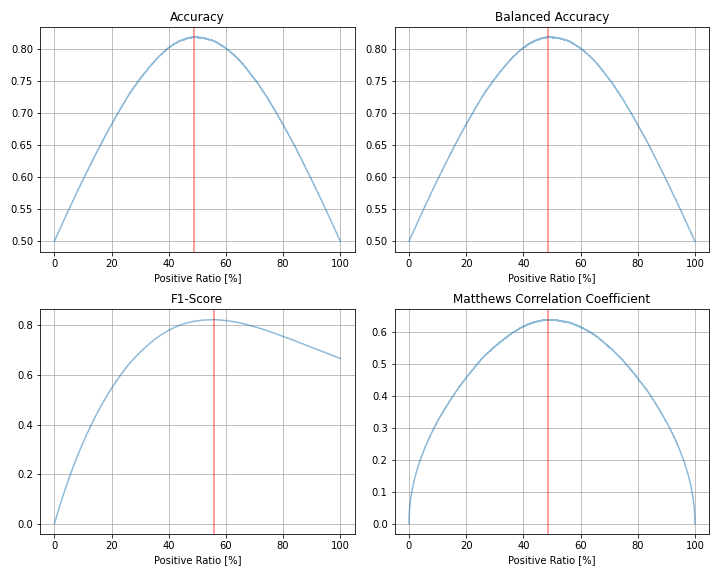
閾値を下げるほど1と予測する割合は増えるため、両図で横軸は反転する対応関係にあります。今回の検証では、予測値の順序のみに結果が依存するため、予測値の値そのものに依存しないこちらの図で考察を行います。
閾値を動かしたときの各指標の最大値と、そのときの予測値=1の割合(上図の赤線)を表にまとめると、以下の通りです。
| 評価指標 | 最大値 | 最大時の予測値=1の割合 |
|---|---|---|
| Accuracy | 0.819 | 48.67% |
| Balanced Accuracy | 0.819 | 48.67% |
| F1スコア | 0.823 | 55.71% |
| Matthews相関係数 | 0.638 | 48.67% |
正例と負例が半々のデータなので、AccuracyとBalanced Accuracyは完全に一致します。また、当然と言えば当然ですが、Accuracy、Balanced Accuracy、Matthews相関係数では、ほぼ半数を1と予測したときに最大値を取っています。(ちょうど50%でないのは、たまたまです。)
一方でF1スコアが最大となるのは、約56%の予測値を1と予測したときになります。また、グラフを見ればわかるように、全ての予測値を0としたときのF1スコアは0ですが、全ての予測値を1としたときのF1スコアは0.6と0.7の間に来ています。これらは、F1スコアの定義の部分で説明した性質によるものです。
以降では、正例と負例の割合をインバランスにしたとき、これらの指標の挙動がどのようになるのかを見ていきます。
2.2. 正例の割合が25%の場合(正例:負例 = 25000:75000)
正例が全体の25%を占めるような二値分類タスクを考える場合です。比較のため、先ほどと同じように、AUCが0.9になるような予測値を生成しています。
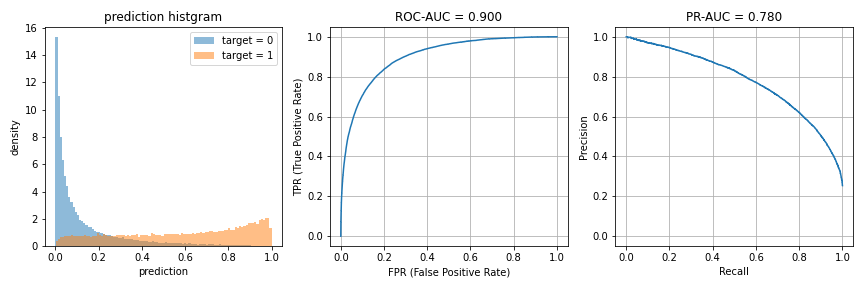
正例の数が減ってしまうため、データ数ではなく密度(density=True)でヒストグラムを描画しています。同じROC-AUC = 0.9でも、インバランスになったことでPR-AUCは若干低くなっています。
次に、先ほどと同じように、閾値を動かしたときの各評価指標の変化をプロットしてみます。
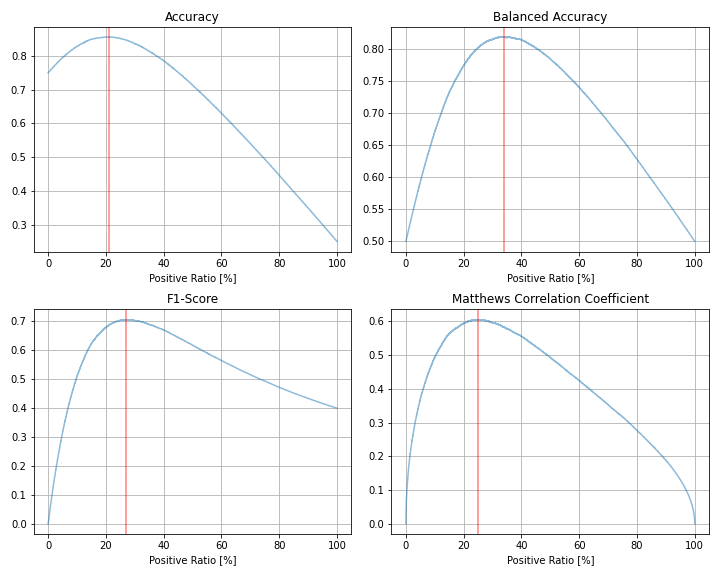
| 評価指標 | 最大値 | 最大時の予測値=1の割合 |
|---|---|---|
| Accuracy | 0.856 | 21.12% |
| Balanced Accuracy | 0.819 | 34.10% |
| F1スコア | 0.706 | 26.99% |
| Matthews相関係数 | 0.605 | 24.84% |
Accuracyは参考までに載せていますが、インバランスデータでは不適切な指標なので、以後は特に考察しません。
F1スコアは全体の約27%、Matthews相関係数は全体の約25%を1と予測したときに、それぞれ最大となっています。これらは、実際の正例の割合25%に近い割合です。
一方、Balanced Accuracyでは、約34%を1と予測したときに最大となっています。後で見ますが、インバランスになればなるほど、Balanced Accuracyと他の指標では最適な閾値が乖離する傾向にあります。
2.3. 正例の割合が10%の場合(正例:負例 = 10000:90000)
今度は、正例が全体の10%の場合です。
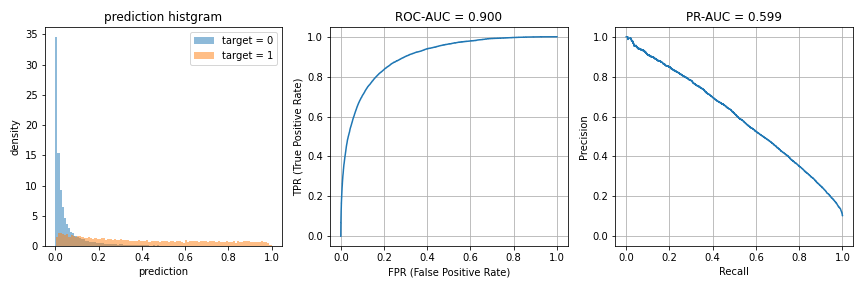
ROC-AUC = 0.9に対し、PR-AUCは0.6程度しか出ていません。
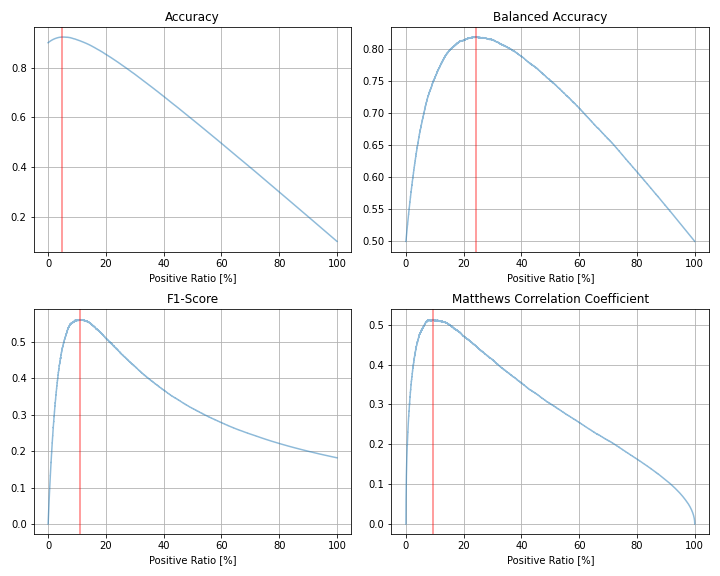
| 評価指標 | 最大値 | 最大時の予測値=1の割合 |
|---|---|---|
| Accuracy | 0.923 | 4.89% |
| Balanced Accuracy | 0.819 | 24.24% |
| F1スコア | 0.561 | 10.94% |
| Matthews相関係数 | 0.513 | 9.43% |
F1スコアは全体の約11%、Matthews相関係数は全体の約9%を1と予測したときにそれぞれ最大となり、実際の正例の割合10%に近い割合になっています。
一方、Balanced Accuracyは約24%のときに最大となり、他の指標との差はより顕著になっています。
また、値の大きさは、Balanced Accuracyの最大値が約0.82に対し、F1スコアとMatthews相関係数は0.5台です。AUCが0.9と聞くとかなり予測できていそうな印象がありますが、これぐらいインバランスになってくると、F1スコアやMatthews相関係数はこの程度の値しか出ないということですね。
2.4. 正例の割合が1%の場合(正例:負例 = 1000:99000)
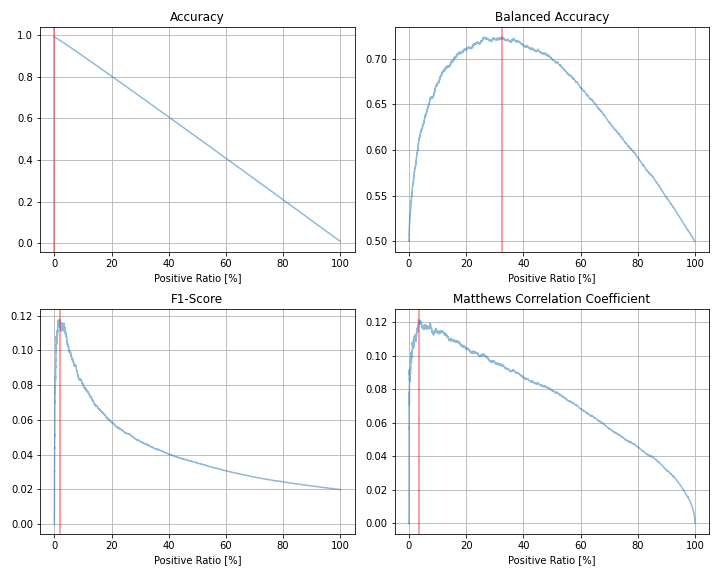
さらに、正例が全体の1%と、かなりインバランスな場合です。
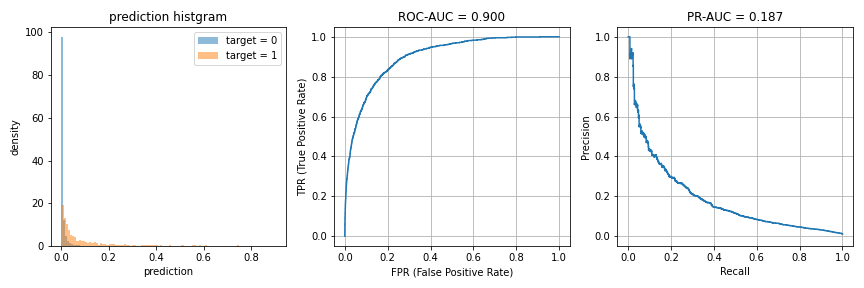
もはやPR-AUCは0.2未満になっています。
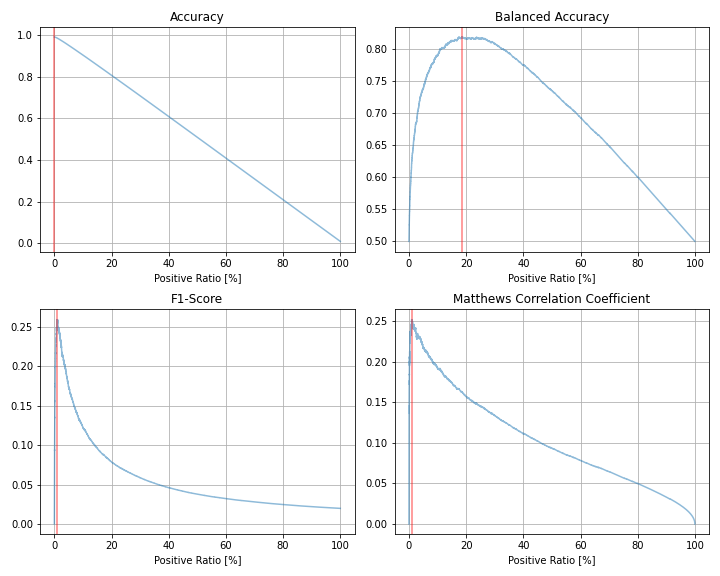
| 評価指標 | 最大値 | 最大時の予測値=1の割合 |
|---|---|---|
| Accuracy | 0.990 | 0.03% |
| Balanced Accuracy | 0.819 | 18.62% |
| F1スコア | 0.259 | 0.94% |
| Matthews相関係数 | 0.252 | 0.94% |
F1スコア、Matthews相関係数ともに最大となるときの閾値は(たまたまですが)全く同じで、そのときの1と予測する割合は全体の約0.9%でした。やはり、実際の正例の割合1%に近い割合です。しかし、最大値は両者とも0.25台という低い数字に留まっています。
一方、正例が1%しか存在しないデータにも関わらず、Balanced Accuracyを最大化するには約19%の予測値を1とする必要があるようです。
また、F1スコアにおいては、1と予測する割合を増やした時のピークからの減衰が激しく、他の指標に比べて閾値に対してセンシティブであると言えるかもしれません。
参考までに、それぞれの評価指標が最大となる場合の混同行列を確認してみます。
- (1) Balanced Accuracyが最大となるケース
| 予測値 | |||
|---|---|---|---|
| 0 | 1 | ||
| 実測値 | 0 | 81200 | 17800 |
| 1 | 183 | 817 | |
- (2) F1スコア、Matthews相関係数が最大となるケース
| 予測値 | |||
|---|---|---|---|
| 0 | 1 | ||
| 実測値 | 0 | 98315 | 685 |
| 1 | 749 | 251 | |
それぞれのケースでの各評価指標の値は以下の通りです。
| 評価指標 | ケース(1) | ケース(2) |
|---|---|---|
| Accuracy | 0.820 | 0.986 |
| Balanced Accuracy | 0.819 | 0.622 |
| F1スコア | 0.083 | 0.259 |
| Matthews相関係数 | 0.163 | 0.252 |
ケース(1)の混同行列を見ると、Balanced Accuracyを最大化する場合、約0.82のRecallを達成できる代償として、極めて多くのFalse Positive(誤検知)を発生させており、Precisionは0に近いことがわかります。そのため、F1スコアは極めて小さい値となってしまいます。
False Negative(見逃し)のペナルティが極めて大きいタスクでは、こちらの方が望ましいことがあるかもしれませんが、少しやり過ぎな感がありますね。Balanced Accuracyがあまり言及されない(=あまり使われていない?)のはこういうところに理由があるのかもしれません。
一方、ケース(2)の混同行列は比較的リーズナブルな感じを受けます。F1スコアはPrecisionとRecallのバランスを取る指標なので、当たり前と言えば当たり前なのですが。(もちろん、これがよいかどうかは、タスクの性質によります。)
3. まとめ
まず、ここまでに示した結果のポイントを事実ベースで整理します。
- 今回の検証では、AUC = 0.9を保ったままインバランス度合いを変化させたが、F1スコアとMatthews相関係数は偏りが大きくなるにつれ最大値が小さくなり、正例が1%のケースでは0.25程度しか出なかった
- PR-AUCも同様に、インバランス度合いが大きくなるにつれ、値が小さくなっていった
- 一方、Balanced Accuracyの最大値はインバランス度合いを変化させてもほとんど変化しなかった
- Balanced Accuracyは、他の指標に比べ正例の検出(Recall)に重きが置かれており、インバランスになるほどその差は顕著であった
- インバランス度合いが強いほど、F1スコアとMatthews相関係数は最適値付近の傾向が近しくなった
じゃあ結局どれを使うのがいいのか、って聞きたくなると思うんですが、今回の検証だけで結論付けるのは横暴ですし、そもそもケースバイケースと言えるので、そのようなことはしません。
重要なのは、ROC-AUCやF1スコアなどの数値だけから安易に性能イメージを掴んでしまうのはミスリーディングになりうるということと、用いる指標によって最適となる閾値は大きく変わりうるということかと思います。ROC-AUCの水準によっては、インバランス度合いが強くても、F1スコアとMatthews相関係数の傾向が変わりうることを、後述のおまけの部分で示しています。
あと、インバランス度合いが強いデータほど、特にF1スコアは0/1の割合によって値が結構変わりそうなので、気を付けた方がよいかもしれません。例えば、複数のモデルからベストを選択するような場合を考えたとき、手法や特徴量の癖によって予測値の分布は変わりうると思います。その際、同じ閾値で切ったとしても0/1の割合は変わりうるため、単に予測値の0/1の割合による差異が、モデル自体の性能の差異のように見えてしまうかもしれません。(だからこそ、連続値による評価指標も合わせて使うべきなのだと思いますが。)
そもそも、ここまで書いてきてこんなことを言うのもあれなんですが、実アプリケーションにおける要求がある程度明確ならば、これらの指標を天下り的に使うよりも、それに直接紐付くような評価を行う方が望ましいと思います。
仮に、見逃しを10%程度に抑えたい、という具体的な要求があるのであれば、例えばRecallが0.9となるように閾値を引いたときのPrecisionの値を評価指標にすれば、より明確に性能をイメージできますし、もし誤検知や見逃しにより発生するコストを試算できるのであれば、混同行列からコストの期待値を計算して評価指標にすれば、それが実用に耐えうるモデルなのかどうかの判断材料になります。(分割の閾値も、そのような観点で決定するべきでしょう。)
もちろん、全てのケースでその辺の要求が明確とは限らないと思いますので、状況によってはここで述べた評価指標を使う場面もあるかと思います。そういったときに、本記事の内容が何かの役に立ちましたら幸いです。
というわけで、あまりまとまりのない記事になってしまいましたが、この辺でひとまず結びとします。以下、おまけです。
4. おまけ
4.1. おまけ1:テストデータをランダムサンプリングしたときの各指標の相関
テストデータをランダムサンプリングすると、閾値が同じであっても評価指標の値は当然ばらつきます。ここでは、正例が全体の1%のケースにおいて、テストデータの半数をサンプリングすることを乱数を変えて1000回繰り返し、各指標の相関を確認します。(ここでは、1と予測する割合ではなく、2.4.の実験で求めた最適閾値を採用し固定します。)
まずは、ケース(1)のBalanced Accuracyを最適とする閾値を採用した場合の各指標の散布図行列です。
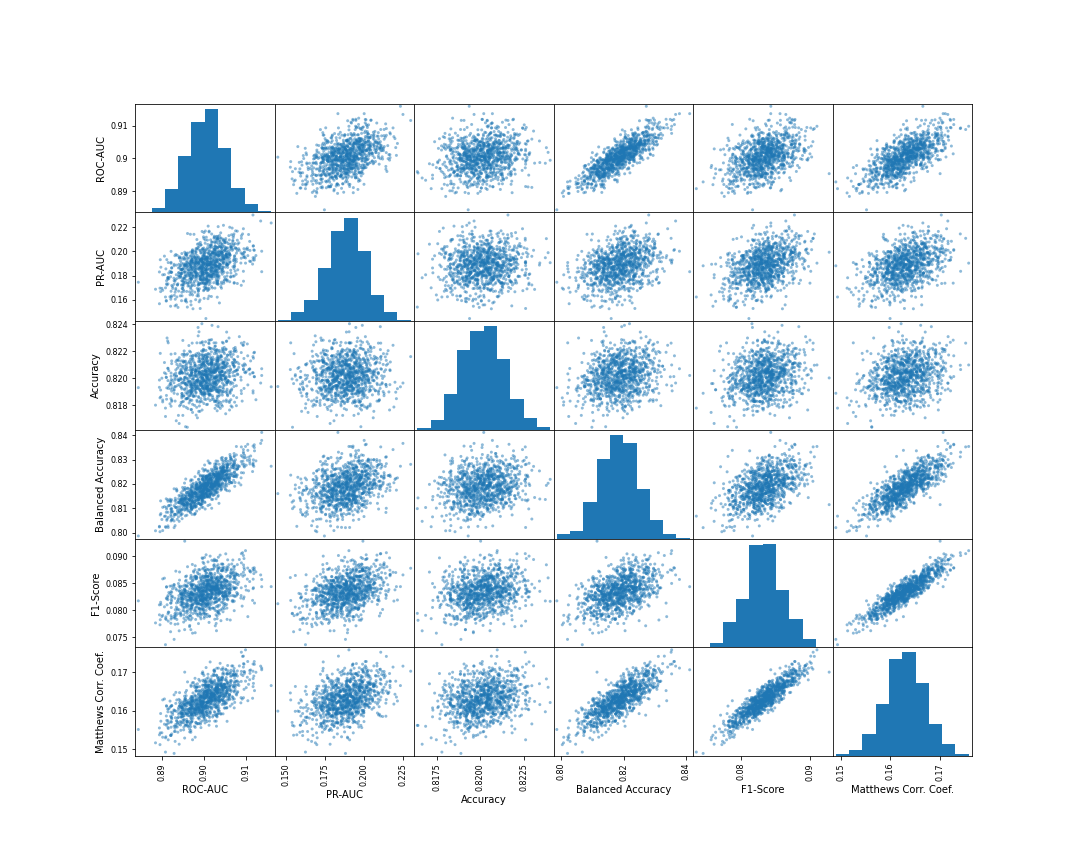
これを見ると、F1-ScoreとMatthews相関係数の相関は比較的強いですが、それらとBalanced Accuracyの相関はやや弱く見えます。
また、ROC-AUCとはBalanced Accuracyが最も相関していますが、Matthews相関係数についても、PR-AUCに比べROC-AUCの方が相関が強そうに見えます。
次に、ケース(2)のF1スコアおよびMatthews相関係数を最適とする閾値を採用した場合です。
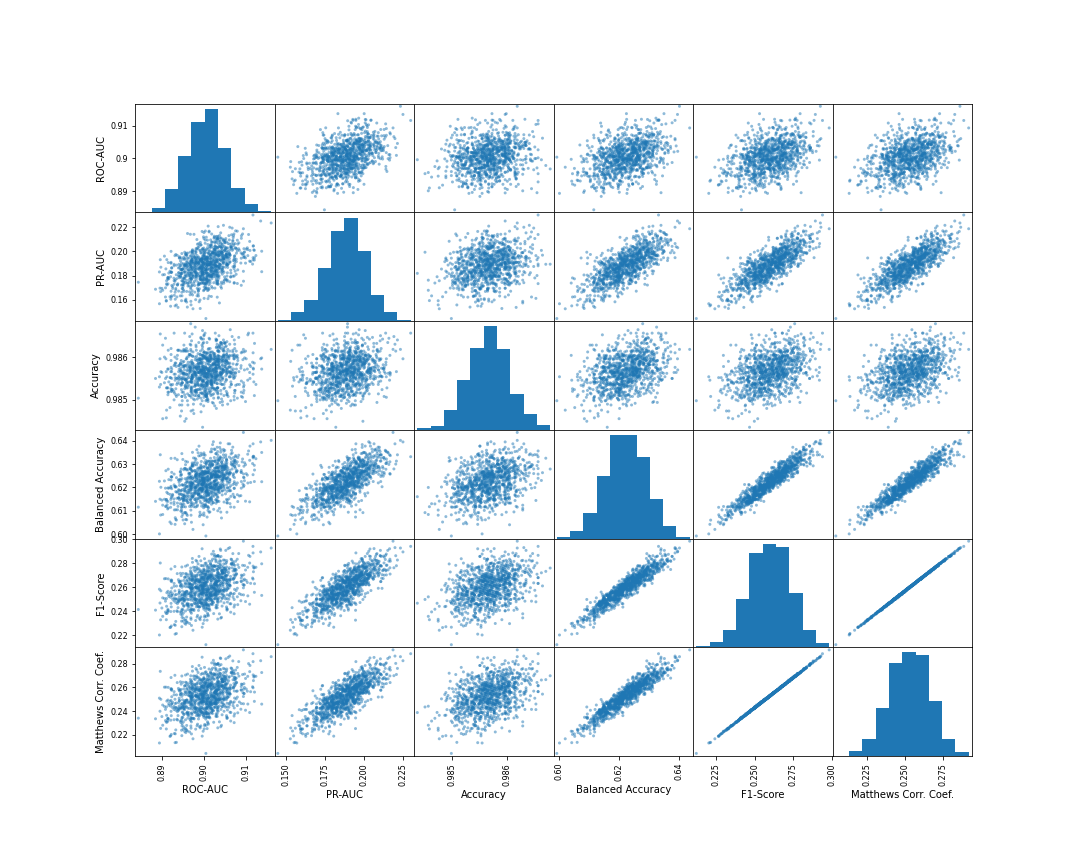
各指標間の相関が先ほどよりも強くなっており、F1スコアとMatthews相関係数はほぼ同じ傾向を示しています。
また、先ほどと異なり、どの指標においても、ROC-AUCよりもPR-AUCとの相関が強くなっています。ケース(2)は上位0.9%を1と予測するような閾値であるため、予測を全体的に評価するROC-AUCよりも、特に上位の予測を重要視するPR-AUCの方が相関が強くなった、と解釈できます。
したがって、連続値のまま評価を行う場合は、最終的にどの程度の割合を1と予測するのかによって、ROC-AUCとPR-AUCのどちらを使うべきかが変わる、と言えそうです。(もちろん、これ以外の観点もあるとは思いますが。)
4.2. おまけ2:F-beta Score(正例:負例 = 1000:99000)
F1スコアの拡張として、PrecisionとRecallの重み付けを変えたF$_{\beta}$スコアがあります。
$$ F_{\beta} = (\beta^2 + 1) \cdot \frac{\text{Precision}\cdot \text{Recall}}{(\beta^2 \cdot \text{Precision} + \text{Recall})}$$
Precisionに$\beta^2$がかかっているので、$\beta$が大きいほどPrecisionが重視されるかのように見えるかもしれませんが、実際には逆で、$\beta$が大きいほどRecallが重視されます。($\beta = 0$ のとき $F_\beta = \text{Precision}$ 、 $\beta \rightarrow \infty$ のとき $F_\beta \rightarrow \text{Recall}$であることからわかります。)
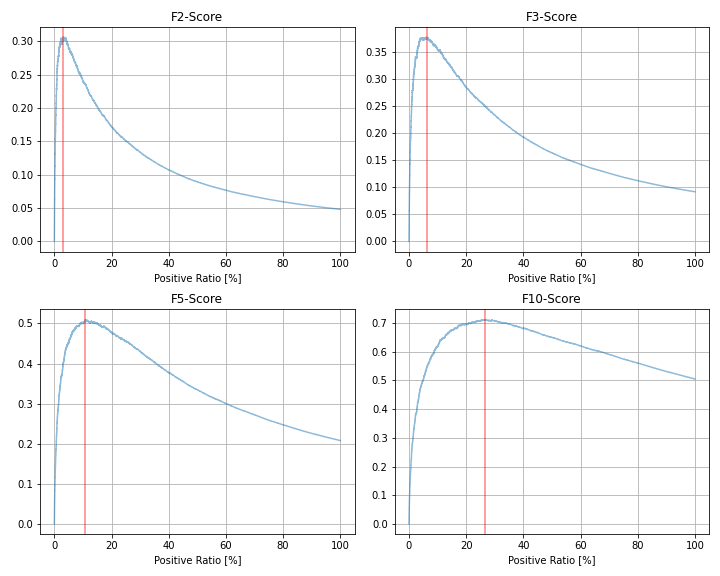
正例が全体の1%のケースに対して、$\beta = 2, 3, 5, 10$としたときの指標の変化をそれぞれ描画してみました。
| 評価指標 | 最大値 | 最大時の予測値=1の割合 |
| --- | --- | --- | --- |
| F1スコア | 0.259 | 0.94% |
| F2スコア | 0.307 | 3.03% |
| F3スコア| 0.378 | 6.28% |
| F5スコア| 0.510 | 10.87% |
| F10スコア| 0.712 | 26.46% |
$\beta$が大きいほどRecallの重みが大きくなるため、1と予測する割合をより大きくした方が最適という傾向になっており、指標の値自体も、高い値を取りやすくなっています。
4.3. おまけ3:AUCを変化させた場合(正例:負例 = 1000:99000)
今回の検証ではAUC = 0.9となる予測値を生成していましたが、これがAUC = 0.99だとどうなるのか、正例が全体の1%のケースに対して、やってみました。
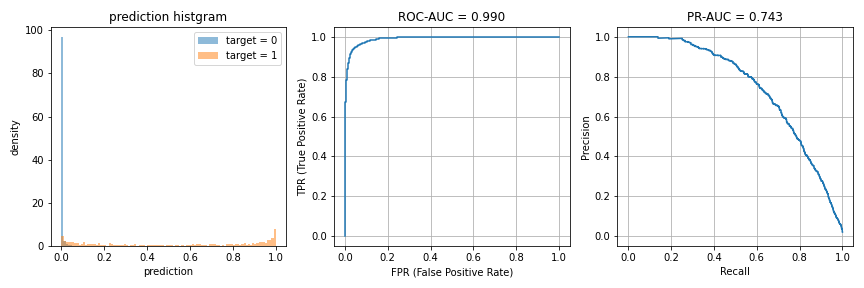
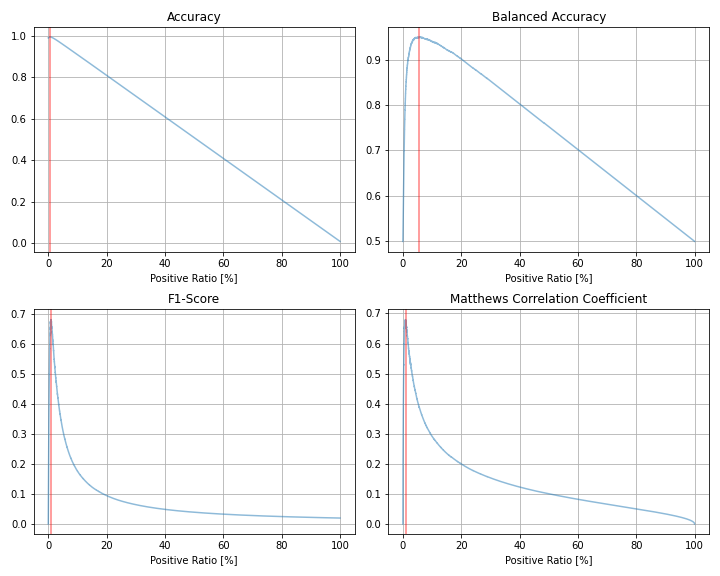
| 評価指標 | 最大値 | 最大時の予測値=1の割合 |
|---|---|---|
| Accuracy | 0.994 | 0.69% |
| Balanced Accuracy | 0.950 | 5.67% |
| F1スコア | 0.682 | 0.92% |
| Matthews相関係数 | 0.680 | 0.92% |
F1スコアとMatthews相関係数がそれぞれ最適となる閾値は、今回も全く同じでした。また、1と予測する割合は約0.9%と、AUC = 0.9のときと同程度となっています。一方、Balanced Acccuracyが最適となる場合の1と予測する割合が減っており、他の指標との差異が小さくなっていることがわかります。
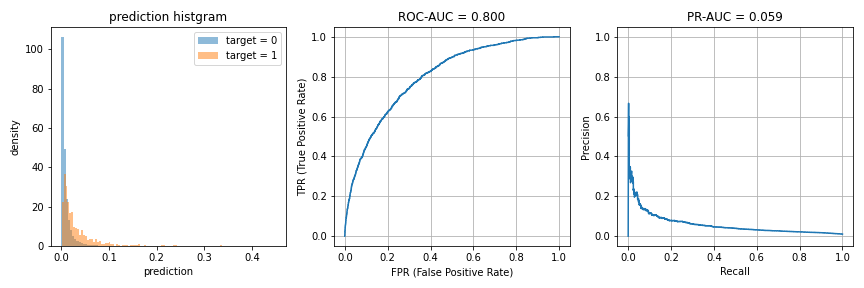
| 評価指標 | 最大値 | 最大時の予測値=1の割合 |
|---|---|---|
| Accuracy | 0.990 | 0.00% |
| Balanced Accuracy | 0.724 | 32.52% |
| F1スコア | 0.118 | 2.01% |
| Matthews相関係数 | 0.122 | 3.35% |
ROC-AUC = 0.9, 0.99のときに比べ、より正と予測する割合が(Accuracy以外で)多くなる結果となっています。また、F1スコアとMatthews相関係数の傾向にも差異が生じており、F1スコアでは約2%、Matthews相関係数では3%の予測に1を割り当てるのがそれぞれ最適という結果になりました。