※本記事はTensorflowにおけるLopに記載された内容を前提としています
入力を$M$次元の$x$, 出力を$N$次元の$y$とする関数$f(x)$について考えます。このとき、ヤコビアン$J$は以下のように定義されます。
J = \left(
\begin{array}{cccc}
\frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \ldots & \frac{\partial y_{1}}{\partial x_{M}} \\
\frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \ldots & \frac{\partial y_{2}}{\partial x_{M}} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial y_N}{\partial x_1} & \frac{\partial y_N}{\partial x_2} & \ldots & \frac{\partial y_{N}}{\partial x_{M}} \\
\end{array}
\right)
この$J$に対して長さ$M$のベクトル$v$を右からかけたのが、Jacobian vector products (jvp)です。R-operator(Rop)とも呼ばれます。
jvp = J v
左からベクトルをかけるL-operator(Lop)と異なり、Ropはtensorflowの仕組み上、直接的には計算できません。
そこで、このブログで紹介されているLopを2回使うことでRopを実現する方法を用います。
原理を簡単に説明します。まず、ヤコビアン$J$に左から適当な長さ$N$のベクトル$w$をかけて転置した$g$を計算します。これはLopなので簡単に計算可能です。
g = [w^TJ]^T = J^T w
このとき、$g$のshape=$[M,1]$となります。次に$g$を、$x$ではなく$w$で微分し、左から長さ$N$のベクトル$v$をかけて転置した$h$を計算します。これもLopなので計算可能です。
h = [v^T \frac {\partial }{\partial w} (J^Tw)]^T = [v^T J^T]^T = Jv
これはまさに最初に求めようとしていたRopです。この2回のLopでRopを実現するtrickはtensorflowで直接実装することができます。以下にtensorflowでの実装例を示します。(実用上は$x$がTensorのlistになることが多いため、もう少し複雑な実装になります。詳しくはissueからリンクがはられた実装例を参照してください。)
def Lop(f, x, v):
return gradients(f, x, grad_ys=v)
def Rop(f, x, v):
w = tf.ones_like(f)
return Lop(Lop(f, x, w), w, v)
これでRopを使うだけなら十分です。
Ropの内部構造
数式上はRopがLop2回で成り立つことはわかりました。では、tensorflowではLopが計算できるケースではRopが常に計算できるのでしょうか?
答えは残念ながらノーです。なぜなら、このRopでは計算グラフを構成する各Operatorの2階微分が必要となるため、2階微分をサポートしていないOperatorを用いている場合には計算できません。
Ropの計算過程を簡単なグラフ例で考えます。まず、以下のような入力$x$に対して、Operator $f$を適用し、さらにOperator $g$を適用するケースを考えます。
f = f(x)
g = g(f)
今求めたいRopは、$g$の出力の各要素を$x$の各要素で微分して求まるヤコビアン$J=\frac{\partial g}{\partial x}$に対し、右からベクトル$v$をかけた$Jv$です。
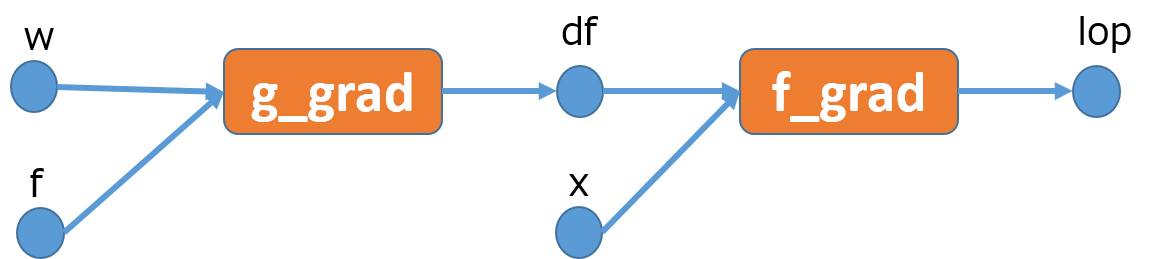
これを求めるために、まず、Lopで$wJ$を求めます。これはtensorflow上では、
f = f(x)
g = g(f)
lop = tf.gradients(g, x, grad_ys=w)
と書けます。このように書くとtensorflowでは次のような計算グラフを生成します。
ここでf_grad, g_gradはそれぞれf(x)とg(f)に対応する勾配関数です。勾配関数は一般的には引数として、元になった関数の入力すべてと、損失Lに対して元になった関数の出力に関する勾配を取ります。
今回のケースでは損失Lが明示的に出てきていませんが、grad_ys=wとしたことにより、$L=w^Tg$となるような損失Lがあるかのように計算されます。よって、g(f)の勾配関数g_gradが受け取る引数は、g(f)の入力であるfと、損失Lのgに関する勾配$\frac{\partial L}{\partial g} = \frac{\partial w^Tg}{\partial g} = w$となります。f_gradも同様にf(x)の入力であるxと、勾配$df = \frac{\partial L}{\partial f}$を入力として受け取ります。$\frac{\partial L}{\partial f}$を計算するのはg_gradの責任です。
このようにして得られたlopは
lop = \frac{\partial L}{\partial x} = [\frac{\partial L}{\partial g}\frac{\partial g}{\partial x}]^T = [w^T J]^T
となります。lopを得るにはf, f_grad, g_gradの計算が必要になります。gは必要ありません。
次に、このlopとベクトル$v$の積$L_2=v^TJ^Tw$を$w$で微分します。これは
rop = tf.gradients(lop, w, grad_ys=v)
と書きます。
これに対して$Lop(f, x, w)$を計算すると、次のような計算グラフが構築されます。
f_grad_gradとg_grad_gradはそれぞれf_gradとg_gradの勾配関数です。勾配関数は元の関数の各入力に関する勾配を出力するので、f_grad_gradとg_grad_gradが出力するTensorは2つなのですが、簡略化のため省いています。
このようにして得られたropは
\begin{align}
rop &= \frac {\partial L_2}{\partial w} \\
&= [\frac{\partial L_2}{\partial lop} \frac{\partial lop}{\partial w}]^T \\
&= [v^T \frac{\partial}{\partial w}(J^T w)] ^T \\
&= [v^T J^T] ^T = Jv
\end{align}
となり、求めていたものであることがわかります。
最終的に、ropを求めるのに、f, g_grad, f_grad_grad, g_grad_gradの計算が必要になります。おもしろいのは、ropの計算にはlopが不要であるため、f_gradが計算されなくなる点です。lopがf, f_grad, g_gradの評価で済むことを考えると、ropの計算コストはlopと比べて上昇する可能性が高いでしょう。
Discussion
RopをLop2回で計算するtrickを説明したブログでは、Lop2回で実装したRopとtheanoの機能で実装したRopが等価な計算グラフに最適化される例が示されており、Lop2回での実装が、十分に効率的である可能性が示唆されています。
しかし、FusedBatchNormとFusedBatchNormGradのように中で行われている計算がC++にしか記述されていない場合、TensorflowのGraph Optimizerから隠蔽されているため、RopはLop2回分のコストを支払う必要がある可能性が高いです。
Ropの論文とそれを実装していると思われるtheanoではRopの計算コストはLopとほとんど変わらない筈です(たぶん)。それに比べてLop2回でRopを実現する手法では、計算時間や各オペレーターの二階微分が必要という点で不利です(ただし、theanoでは各OperatorにRopの定義が必要と思われる)。
(おまけ)Ropの別実装
計算過程で使われるベクトル$w$はグラフの最適化で消えるべきだという信念を利用したRopの実装案がこちらのissueで提案されています。概要は以下のようになります。
def Rop(f, x, v):
w = tf.placeholder(f.dtype, shape=f.shape())
return Lop(Lop(f, x, w), w, v)
先ほどのRopの実装と異なり、$w$がones_likeからplaceholderに変更されています。もし、$w$が除去されずに計算グラフに残った場合、このRopを計算しようとすると「placeholderの値がfeed_dictで指定されていない」旨のエラーが発生するため、無駄な演算を検知することができます。
こちらのRopは無駄な演算を検知することはできるのですが、実用上は計算グラフの最適化で$w$への依存を除去しきれないケースがあるため、placeholder版ではRopで計算できる範囲が狭まってしまいます。