Pythonで粒子のスピンを操ろう！: 磁石とはなんぞや？

あらまし

以前書いた Pythonで自然発生する交通渋滞を見よう！ と似たような数理モデル一発ネタであります
今回はかなり物理寄りのお話です¹

Ising模型

強磁性体を記述するモデルのひとつです. 強磁性体というのは磁石みたいな、スピンが揃っている系のことを指します. たとえば、磁石を構成する原子が持つスピンはそれ自体が小さな磁石みたいなもので、彼らの向きが揃うことでマクロな磁化(磁石の強さみたいなもの)を持つことになります. 逆に、スピンの向きがバラバラなら磁石として機能しなくなります.

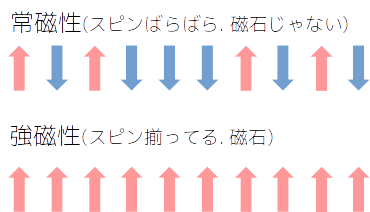
中学生くらいの頃、磁石を加熱すると金属がくっつかなくなるで！！的な実験をしたことがあるかもしれません. これは熱によって揃っていたスピンがバラけてしまい、磁化が弱まったことに依ります. この現象をPythonでシミュレートしてみましょう.

スピンと聞くと、量子論的な難しい話になるかなーと思われるかもしれませんが、解析的に扱おうとせずにイメージで捉える限りそんなに難しくないです. Ising模型自体はとても解釈しやすいシンプルな統計力学のモデルです.

数学的準備: Ising模型の意味

今回は2次元Ising模型を扱います. ハミルトニアンはこんな感じ:
$$
H = -J\sum_{\langle i, j\rangle} s_i s_j
$$

$\langle i, j\rangle$ は隣接サイトのスピンを表します. 相互作用するのは隣同士のスピンだけです. $J$は相互作用定数で、スピン間の相互作用の大きさを表します. $s_i, s_j$ がスピンで、アップスピンを1, ダウンスピンを-1とします.

ハミルトニアンは系の内部エネルギーを表しているので、上の式が言っていることは、**「スピンが揃っている(スピンの積が正)と内部エネルギーは小さくなる」「スピンがばらついている(スピンの積が負)と内部エネルギーは大きくなる」**ということです.

このモデルを磁化のはなしに繋げるために、ヘルムホルツ自由エネルギーの定義を引っ張ってきましょう:
$$
F = U - TS
$$

熱力学を思い出してください. 系の平衡状態はヘルムホルツエネルギーが最小になるように選ばれます. 上の式を見ると、例えば、高温($TS > U$)では$F$を小さくするために、エントロピー$S$が大きくなります. つまり、スピンがばらけるわけです. 一方、低温($TS > U$)では内部エネルギー$U = \langle H \rangle$が小さくなります. これはスピンが揃っていることに対応しますね.

熱力学の定義に当てはめて、磁石の現象を再現する最もシンプルなモデルがIsing模型です.

数学的準備: コーディングに向けて

(※注) かなり統計力学に突っ込んだ話になります. アルゴリズムだけをかいつまみたい方は結論に飛んでください.

さて、Ising模型の概要がなんとなくわかったところで、解析的な話を大方ぶっとばしてコーディングの準備に入ります. 今回興味があるのは以下の2点です:

1. 適当なスピンマップを持ってきて、温度を下げていくと磁区(スピンが揃っている領域)が自発的に形成されること
2. 温度を上げていくとスピンがバラけていくこと

ここで考えなければならないことがあります. ヘルムホルツエネルギーが内部エネルギーに強く依存するような低温下ではスピンが揃っていきますが、ただ$F$を小さくするようにスピンをフリップさせるコードを書くと全スピンが単一方向を向くことになります². まあ絶対零度ならそれでもいいかな、、、とは思いますが、そこから少しずつ温度を上げていくとエントロピーの寄与が効いてきて、スピンの向きが次第にバラけていきます. この「温度によるバラけ」はどのようにして実現されるべきでしょうか？

実現される「べき」と書いたのは、物理を無視すれば温度によるバラけを表すモデルをつくることはいくらでもできるからです. 今回はIsingモデルからスタートして物理で議論を展開してきているので、温度によるバラけ方も物理に紐付いた形でなければなりません. これを統計力学から探っていきましょう.

そもそも平衡状態ってなに？から考えましょう. 統計力学でいうところは平衡は、系のエネルギーがボルツマン(Boltzmann)分布に従うことです. 系にたくさんある各スピンは、ハミルトニアンの定義に従って内部エネルギーを持ちます($-J s_i s_j$). 「適当なスピンマップを持ってきて、、、」のくだりが意味するところは、系のエネルギーがめちゃくちゃな分布であるような状態から、スピンをフリップさせてボルツマン分布に持っていこう！ということです.

仮に系のエネルギーがBoltzmann分布にたどり着いたとして、それ以降はスピンが全く動かないかといったら、そんなことはないです. エネルギーが大きくなるような遷移と小さくなるような遷移が等確率で起きているのが自然です³. これを表すのが以下の式です:
$$
W(E, E')P(E') = W(E', E)P(E)
$$

$P(E)$ が内部エネルギーの分布、$W(E, E')$をエネルギー$E' \rightarrow E$へと遷移する確率です. つまり$W(E, E')P(E')$はエネルギー$E' \rightarrow E$へと遷移する流れと解釈でき、順方向と逆方向の流れの強さが等しければ平衡、ということを意味しています⁴. ここでエネルギー分布$P(E)$の具体系はカノニカル分布の定義により
$$
P(E) = \frac{e^{\beta E}}{Z}
$$

となります. $Z$は分配関数、$\beta = \frac{1}{kT}$は逆温度です. これを先ほどの流れの式に代入すると
$$
e^{-\beta(E - E')} = \frac{W(E, E')}{W(E', E)}
$$

これを満たすようなWとして
$$
W(E, E') = \begin{cases}
1 & (E \leq E') \\
e^{-\beta(E - E')} & (E \geq E')
\end{cases}
$$

を与えることにします⁵.

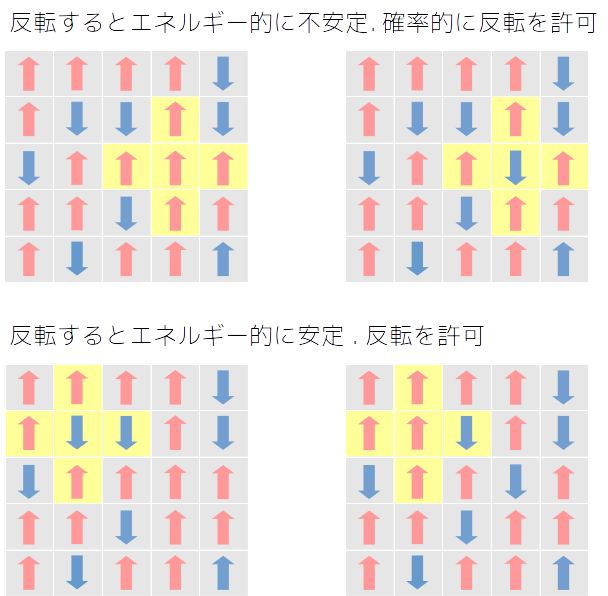
長くなりましたが、上の条件を満たすようにスピンをフリップしていくことになります:

1. スピンをフリップしたときに、エネルギー的に安定する(低くなる)ならばそのままにする
2. スピンをフリップしたときに、エネルギー的に不安定(高くなる)ならば、確率$e^{-\beta(E - E')}$ で反転を許可する

このアルゴリズムをメトロポリス(Metropolis)法と呼びます. これに従ってスピンをフリップしていくと、エネルギーの分布はボルツマン分布に近づいていくことになります.

おまけ

(※注) これもスルーしていただいてOKです

分配関数の具体系は
$$
Z(\omega) = \sum_\omega e^{-\beta E(\omega)}
$$

です. $\omega$ は微視的状態を指します. 今回の例で言えば、スピンの配列が微視的状態にあたります. 分配関数は全ての微視的状態についてのアンサンブルの和です. 詳細は省きますが、分配関数には内部エネルギー$E$が含まれるため、これをハミルトニアンを用いて記述することができます. つまり、$Z$には系の情報が全て含まれていることになります. それに加えて、分配関数には温度($\beta = 1/kT$)が含まれているため、系に温度の情報を付加したことになります. 量子論において有限温度系を扱う場合は、ハミルトニアンを直接弄るのではなく、分配関数を扱っていくことになります. これが量子統計力学です.

先程のメトロポリス法にはヘルムホルツエネルギーを最小にする、という文脈は現れていませんでした. なぜかというと、その情報は分配関数に既に含まれているからです. ハミルトニアンには温度の情報が含まれていないため、最初はIsingモデルとヘルムホルツエネルギーを別々のものとして扱いましたが、分配関数によってそれらをまとめて取り扱えるのです. まさに量子論と熱学の融合！この万能感よ、、、

そもそもの話のスタートは微視的状態であり、今回の例に当てはめればそれはスピンの配列です. そのミクロな情報からマクロな法則を導くのが統計力学です. 大量にあるスピンをひとつひとつシュレディンガー方程式で扱っていくとキリがないので、その全体の振る舞いを調べるためにとても有用な学問です. 分配関数からヘルムホルツエネルギーや内部エネルギーを導出することができることからわかるように、ミクロな情報からスタートし、最終的に熱力学を再現できたことになるのです.

熱力学それ自体はミクロな粒子の存在を扱うものではなく、あくまで熱力学関数を主体に理論を構築しているマクロな学問です. その熱力学が謳う法則を微視的なレベルから導出した天才がボルツマンです.

とても良くできていて面白い学問なので、気になった方は是非勉強してみてください.

コーディング

では、実装していきましょう

import numpy as np
import math as m
from random import randint, random


class Spin(object):
    def __init__(self):
        self.N = 64
        self.J = 1.0
        self.T = 3
        # スピンマップをランダムに初期化
        self._spin_map = np.random.choice([-1, 1], size=(self.N, self.N))
        # スピンマップを1に初期化
        # self._spin_map = np.ones((self.N, self.N))
        self._spin_map_p = [None] * 4
        self.Energy = None
        self.Mag = None

    def get_spin(self, x, y):
        if x == len(self._spin_map[0]):
            x = 0
        if y == len(self._spin_map[0]):
            y = 0
        return self._spin_map[x][y]

    def set_energy(self):
        self._spin_map_p[0] = np.vstack((self._spin_map[1:], self._spin_map[0]))
        self._spin_map_p[1] = np.vstack((self._spin_map[-1], self._spin_map[:-1]))
        self._spin_map_p[2] = np.hstack((self._spin_map[:, -1:], self._spin_map[:, :-1]))
        self._spin_map_p[3] = np.hstack((self._spin_map[:, 1:], self._spin_map[:, :1]))
        self.Energy = -self.J * np.sum(np.sum(self._spin_map_p, 0) * self._spin_map)

    def set_mag(self):
        self.Mag = abs(np.sum(self._spin_map)) / (self.N**2)

    def flip_spin(self):
        # 弄るサイト
        X = randint(0, self.N-1)
        Y = randint(0, self.N-1)

        EnergyBefore = -self.J * self._spin_map[X][Y] * (
            self.get_spin(X+1, Y) +
            self.get_spin(X-1, Y) +
            self.get_spin(X, Y+1) +
            self.get_spin(X, Y-1))

        if EnergyBefore > 0 or m.exp(2 * EnergyBefore / self.T) > random():
            # 反転したらエネルギー的に安定
            # もしくは不安定でも確率的に反転
            self._spin_map[X][Y] = -self._spin_map[X][Y]

コアとなるコードのみ載せました. C/C++で書くとfor文が乱立するところですが、PythonだとNumpyで工夫することによってシンプルにできるのがいいですね.

適当な位置のスピンを反転して、エネルギーが小さくなるならそのままに、エネルギーが大きくなるようであれば確率的に反転を許可するようにします.

また、今回は周期的境界条件を課しています. 端っこのお隣は反対側になります.

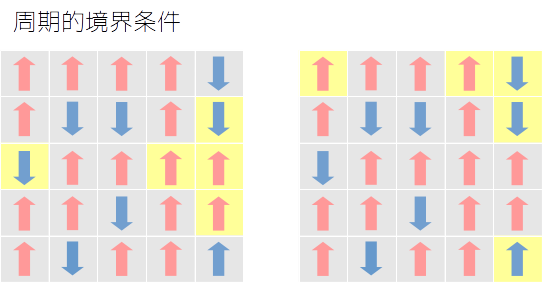
この境界条件を課したうえで、エネルギーを求めるset_energyメソッドはfor文を使わないように少し工夫をしています.

flip_spinメソッドでスピンを何度もフリップさせていくと、温度に応じたスピン配置が得られます. 高温ならバラつき、低温なら揃っていきます. 試しに高温から低温に下げてみましょう:

pic.twitter.com/kRJcWpzKlH

— Jabberwocky (@jabberw75864611) 2018年4月29日

スピンが上下にばらついた状態から、揃った区域(磁区)が形成されていきます. 次はset_magメソッドで磁化を温度でプロットしていきましょう:

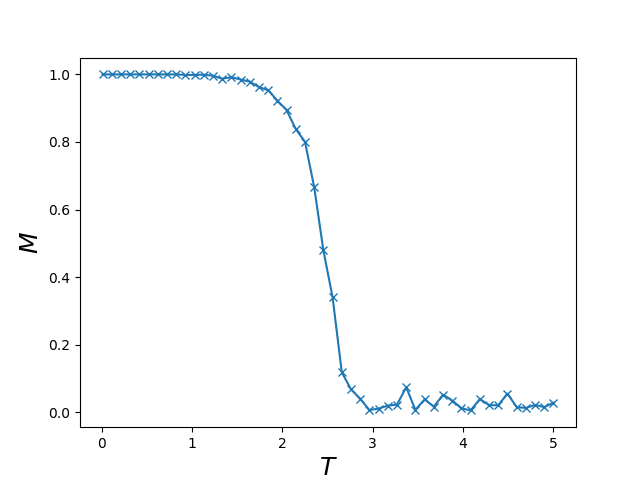
あるポイントで磁化が急激に小さくなっています. これは系が強磁性体→常磁性体に相転移したことを表しています⁶. 言うなれば、温度を上げると氷→水になることと同じです.

相転移は物理において非常に興味深い対象であり、特に非平衡系についてはまだ確固とした理論が完成していないのが現状です. その片鱗をこれだけシンプルなモデルを通して覗くことができるのは楽しいですね.

さらにおまけ

ちなみに、、、

1次元Ising模型を解析的に解くことは、統計力学がわかっていればそんなに難しくありません. では、今回扱ったような2次元のIsing模型はどうかと言うと、かなーり厄介です. その昔、オンサーガー(Onsager)が厳密解を求めましたが、数学的にかなりスパルタンだったようです. オンサーガーはIsing模型を含んだ熱力学関連の業績でもってノーベル賞を受賞しています.

一方で、南部陽一郎先生も2次元Ising模型の厳密解をオンサーガーとは別の解法で求めています. 南部先生もまた、自発的対称性の破れ⁷に関する研究でノーベル賞を受賞しています.

ずいぶんとシンプルなモデルですが、それ故に熱学・統計力学の発展にはなくてはならないモデルであり、その研究には弩級の天才たちの影があります.

1. 物理にお詳しい方から見ると議論に粗が見えるかもしれません. ご容赦. ↩

2. 正確には、初期状態にかなり依存はします. 完全に同一方向に向くようなコードを書くためには少し工夫が必要です. ↩

3. 化学平衡の定義はまさにこれです. 順反応と逆反応が同じ頻度で起きているわけです ↩

4. この関係の元になっているのはMaster方程式と呼ばれる時間発展方程式です. 今回の系の時間発展はMaster方程式で記述できるものと仮定しています. ↩

5. 「与えることにする」と言っているのは、それ以外の選び方もあるからです. ここに物理が介在する余地はありません. ↩

6. 正確には相転移していることを示すには、熱力学関数の微分値が発散している必要があります. 今回の系であれば比熱(エネルギーの温度微分)が発散しています. ↩

7. 相転移とは切っても切れない重要な概念です. ↩