以前書いた Pythonでカオス・フラクタルを見よう! と似たような数理モデル一発ネタであります.
Optimal Velocity Model
坂東昌子さんという素粒子畑の物理屋さんがつくった渋滞モデルです. これは自然渋滞を表現するモデルとして有名です. **「事故なんかなくても車の数がある程度ありゃあ渋滞は起きるよ!」**ということです.
このモデルの骨子は, 前の車との車間距離に応じて目標速度が変化することにあります. 車間距離が大きければ法定速度で走ろうとするし, 小さければ速度を下げようとします. これを微分方程式で表現すると以下のようなものになります:
\frac{d}{dt}x_n = v_n, \hspace{1cm}\frac{d}{dt}v_n = a\left[V(x_{n+1} - x_n) - v_n\right]
$n$ はそれぞれの車の番号で, その前を$n+1$番目の車が走っています. 第一式は単なる速度の定義です. 第二式にある$V(h)$は車間距離に対する目標速度に相当します:
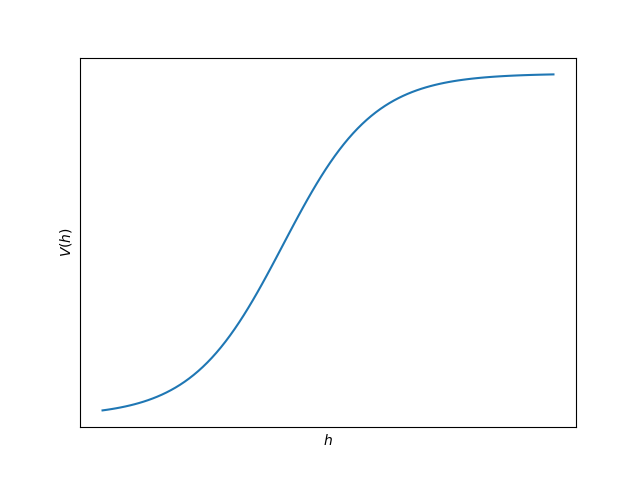
V(h) = \tanh(h - c) + \tanh{c}
$c$ は適当な定数. $V(h)$ はこんな概形です:
車間距離が広がっていくと目標速度はある程度のところで飽和します. いわゆるシグモイドみたいな子です. この$V(h)$が非線形関数であることが非常に重要な役割を果たすのですが, ちょっとディープな話なので省略.
前の式に戻りますが$a$は感受率と呼ばれるパラメータで, 車間距離に対する反応の敏感さを特徴づけています.
モデルの解釈
このモデルで弄ることのできるパラメータは$c$と$a$の2つです. $c$は$V(h)$の概形を変え, $a$は車間距離に対する反応を決めます.
これはつまるところドライバーの性格と解釈することができます. 車間距離が小さくても全然速度を下げようとしない荒っぽいドライバーも居れば, 車間距離がかなり開かないと速度を出せない初心者ドライバーも居るわけです. そういう個性を$c$と$a$というパラメータで表現しようということです.
つまり本来は各ドライバーごとに異なる$c$と$a$が定義されているべきで, $c_n$, $a_n$と書くべきなのでしょうが, 面倒なので全てのドライバーに共通の$c$と$a$を一つ定義することにします. こんな雑な問題設定でも自然渋滞をシミュレートすることができます.
問題設定と実装
30台の車が円状のサーキットを等速度・等間隔で走っています. ここで, 初期時刻 $t = 0$ で誰かさんが軽くブレーキを踏んだとしましょう. その後車の動きはどうなるでしょうか?
import numpy as np
from scipy.integrate import odeint
def trafficJam(f, t, a, c, L):
"""
微分方程式の定義(odeint)
f = [x, v]
"""
x, v = f[:N], f[N:]
def V(h):
return np.tanh(h - c) + np.tanh(c)
x_dot = v
x = np.append(x, [x[0]])
diff_x = np.diff(x)
diff_x = np.array([i if i > 0 else L + i for i in diff_x])
v_dot = a * (V(diff_x) - v)
return np.append(x_dot, v_dot)
# 各定数
N, a, c, L = 30, 1.3, 2, 60
# 初期位置
x = np.arange(N) * L / N
# 初期速度
v = [(1 + np.tanh(c)) / 2] + ([1 + np.tanh(c)] * (N - 1)) # 最初の1台がブレーキをかける
# 時刻
t = np.arange(0, 200, 0.1)
# 微分方程式を解く
var = odeint(trafficJam, np.append(x, v), t, args=(a, c, L), full_output=False)
x_arr, v_arr = var[:, :N], var[:, N:]
— Jabberwocky (@jabberw75864611) 2016年12月21日
みごとに渋滞が発生しています. モデルも実装も単純でいいですね.
こぼれ話: 対称性の破れと相転移
ちょっとマニアックな物理話です. スルーしても大丈夫です.
「スムーズに流れている状態」は円状ほぼ等間隔に車が並んでいるので, 回転対称性があると言えます. 一方で「渋滞している状態」は回転対称性を持っていません. 今回の動画では渋滞が起きている場所が3箇所あり, その渋滞の密度, 位置ともに対称的な配置にはなっていません. つまり対称性が破れたのです.
もし仮に渋滞した3箇所が「おにぎり型」っぽく配置されたいたら3回対称, つまり 回転対称性を保持している1のですが, もともとのスムーズに流れていた状態は30回対称なので, より低い対称性に遷移したことになります. これもまた対称性の破れです.
そして, 対称性の破れと密接な関係にある概念として相転移現象があります. 相転移といえば水→氷(液体→個体)などをイメージされる方が多いと思います. 液体の水は ${\rm H_2O}$ 分子が乱雑かつ大量に存在するので, 高いレベルの空間回転対称性や並進対称性を持っていると考えることができます2. 一方で氷は格子状の構造を持つため, 液体よりも低い対称性に遷移します(ちなみに対称性が低いというのは秩序を持った状態であるということはこの水→氷のたとえ話から直感的にわかると思いますが, この秩序の度合いを定量的に表したものが秩序変数と呼ばれるものです3). つまり, 「スムーズに流れている状態」から「渋滞している状態」は水→氷と似たような相転移現象と捉えることができるわけです.
一般的な相転移現象は対称性の破れを伴いますが, 相転移を記述するためには「非線形」であることが重要で, 今回のOptimal Velocity Modelで言えば$V(h)$が非線形であることが重要だったわけです. 2点相関関数などを取ってあげれば渋滞した状態の秩序変数を定義することもできるかもしれません.
さらにマニアックな話になりますが, いわゆる秩序変数が存在しないのに相転移が起きるような系も存在します. これはBerezinskii-Kosterlitz-Thouless(BKT)転移と呼ばれ, 発見したKosterlitzとThoulessは2016年にノーベル賞を受賞しています4. BKTのBの人はなぜ受賞できなかったかというと, 1980年に亡くなっているからです. 残念.
このように, 対称性の破れ・相転移というのは物理界隈ではとても興味深いモノなのです.