はじめに
深層強化学習の分野では日進月歩で新たなアルゴリズムが提案されています.
それらを学ぶ上で基礎となるアルゴリズム(というより概念に近い?)はQ学習, SARSA, 方策勾配法, Actor-Criticの4つだと思われるので, これらを軸としてまとめてみたいと思います.
以下の4点はあらかじめご了承ください.
- コードは書いていません. 概念のみの説明です
- 他のアルゴリズムの基礎となりうる重要な概念については詳しく書きました. その他については簡潔に書きました
- 深層学習についてはある程度理解している読者を想定しています
- 書いているうちに規模がどんどん大きくなってしまったので, どこかに必ず間違いや不足があります.
「この式がおかしい!」「このアルゴリズムも追加するべき!」などコメントがあればぜひお願いします
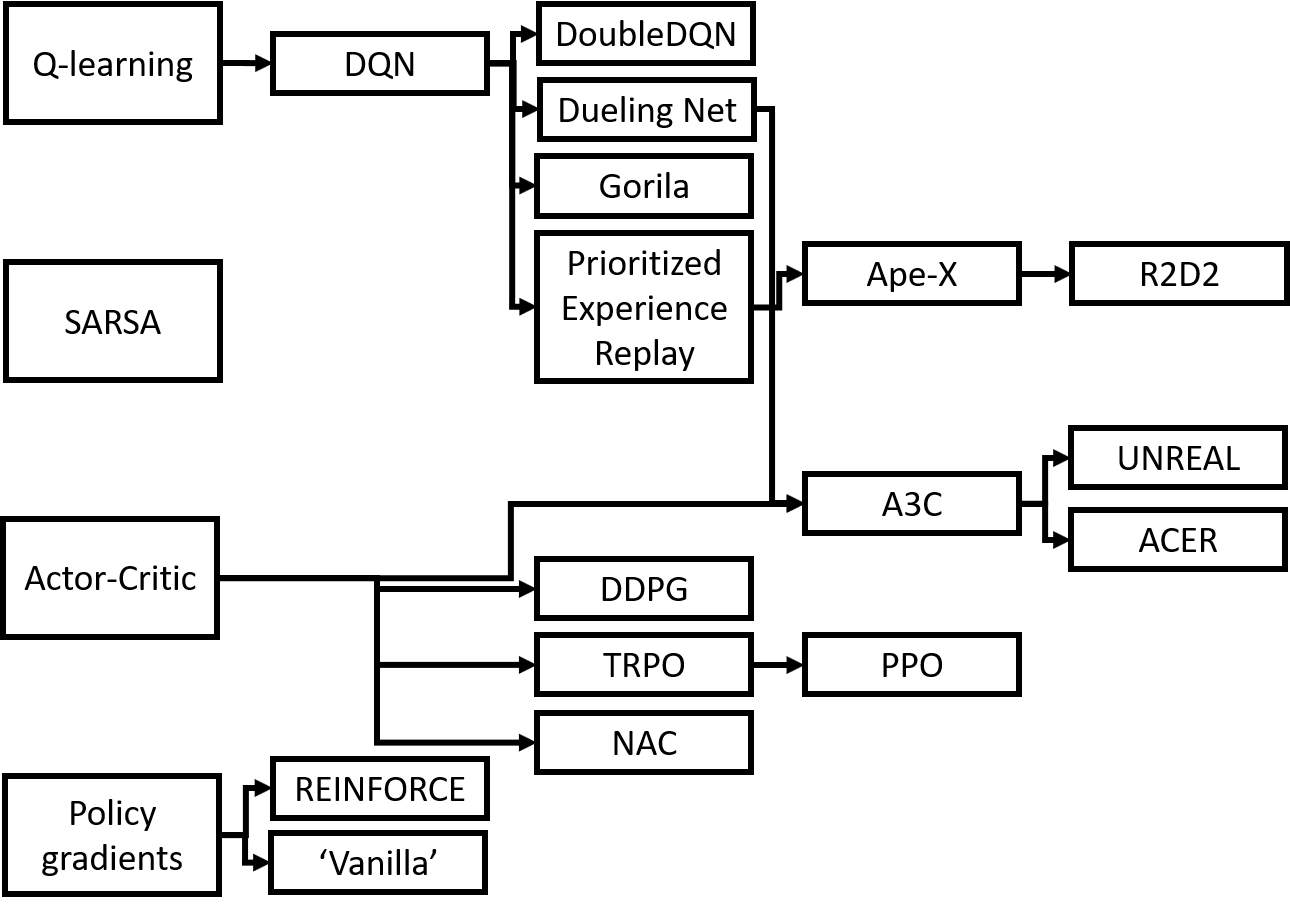
全体像
扱うアルゴリズムを相関図にしてみました(私のイメージです).
まず, これから強化学習アルゴリズムの特徴を記述するにあたって必要な用語・概念を整理しておきます.
ややこしい数式がいろいろ出てきますが, できるかぎりかみ砕いた解説を付けたつもりです.
Suttonの分類によると, 強化学習は動的計画法, モンテカルロ法, TD(temporal difference; 時間的差分)学習の3種類に分けられます.
このうち, 動的計画法はシステムのパラメータが既知の場合にBellman最適方程式を解いて最適な方策を得るというアプローチで, モンテカルロ法は実際に試行を繰り返して得られた報酬から価値を推定するというアプローチです.
実世界のような複雑なシステムではこれらのアプローチは現実的でないため, TD学習が用いられることが多いです.
TD学習は, 実際の報酬から方策関数や価値関数を改善しながらBellman最適方程式を解いていくというアプローチで, (複雑な問題を解きたい)深層強化学習では基本的にTD学習を行います.
したがって, 本記事ではTD学習に基づくアルゴリズムのみを扱います.
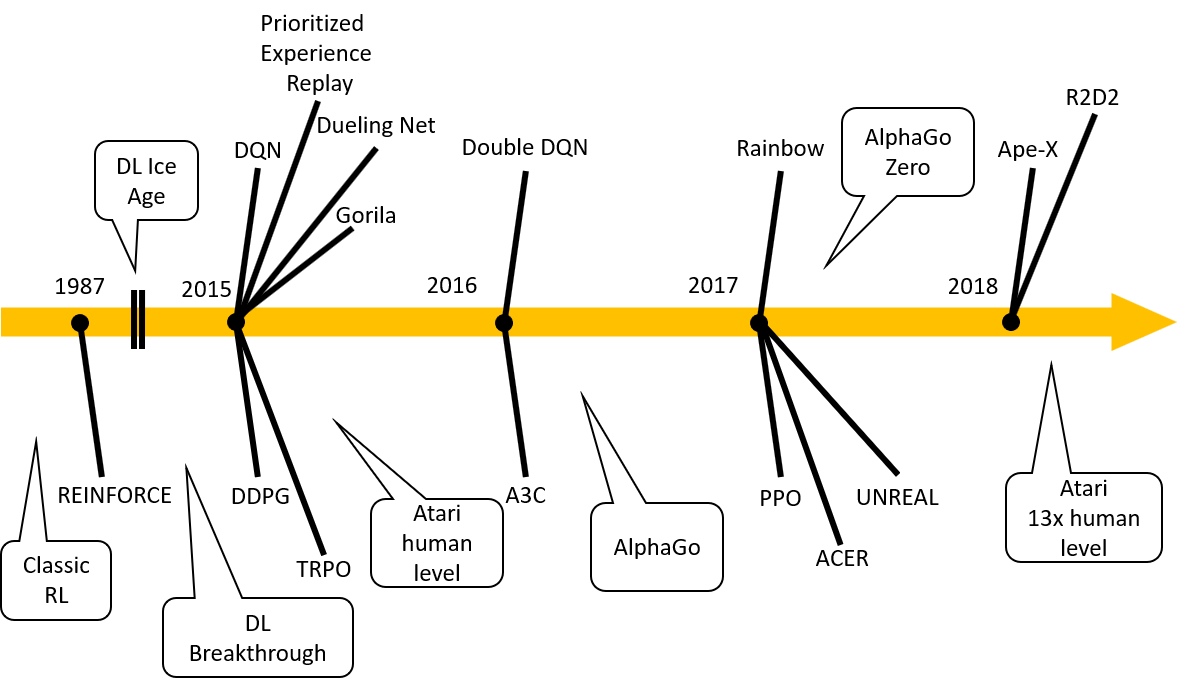
(2020年9月10日追記: えるエルさんが作成した図が新しくより網羅的・体系的なので, 貼っておきます. スレッドに書いてある補足説明もおすすめです. )
東京大学松尾研 深層強化学習サマースクール,講義は昨日無事に終了しました.受講生の皆様お疲れ様でした!
— えるエル (@ImAI_Eruel) September 9, 2020
講義資料を作りながら,いい機会だと思ったので,強化学習のアルゴリズムをまとめた図を作ってみました
強化学習,深層強化学習について大体の流れ,手法を追いたい人は是非ご利用ください! pic.twitter.com/loCRgxWQGE
方策関数
状態$s$を入力として行動$a$を出力(選択)する関数です.
一意な行動を出力する決定的方策と, 行動の確率分布を出力する確率的方策があります.
数式で表すとそれぞれ次のようになります.
\begin{eqnarray}
a &=& \pi(s)\\
\mathbb{P}(a) &=& \pi(a|s)
\end{eqnarray}
価値関数
価値関数には状態価値関数と行動価値関数があります.
状態価値関数は, 方策を$\pi$で固定したとして, 状態$s$から将来もらえると期待できる割引報酬和を表す関数です.
割引率を$\gamma$, ステップを$t$とするとこのように数式で表せます.
\begin{eqnarray}
V^{\pi}(s) &=& \mathbb{E}\bigl[ \bigl. \sum_{i=1}{\gamma^{i-1}r_{t+i}} \bigr| s\bigr]\\
&=& \underset{a,s'}{\mathbb{E}}\bigl[ \bigl. r+\gamma V^{\pi}(s') \bigr| s\bigr]
\end{eqnarray}
2行目の漸化式をBellman方程式と呼びます.
なお, 状態遷移も行動選択(方策)も確率的であるとして, 期待値は$a,s'$に関してとっています.
行動価値関数は, 方策を$\pi$で固定したとして, 状態$s$で行動$a$をとった場合に, 将来もらえると期待できる割引報酬和を表す関数です. Q値とも呼ばれます.
行動価値関数に関しても同様の式が成り立ちます.
\begin{eqnarray}
Q^{\pi}(s,a) &=& \mathbb{E}\bigl[ \bigl. \sum_{i=1}{\gamma^{i-1}r_{t+i}} \bigr| s,a\bigr]\\
&=& \underset{s',a'}{\mathbb{E}}\bigl[ \bigl. r+\gamma Q^{\pi}(s',a') \bigr| s,a\bigr]
\end{eqnarray}
以下では行動価値関数についてのみ考え, 単に「価値関数」と呼ぶこととします.
また, 得られる割引報酬和の最大値を最適価値関数$Q^{*}(s,a)$で表し, そのときの方策を最適方策$\pi^{*}$で表します.
Q^*(s,a) = Q^{\pi^{*}}(s,a) = \underset{\pi}{\max}{Q^{\pi}(s,a)}
このように, 価値関数が最大になるような行動を選ぶ決定的方策をグリーディー方策と呼びます.
Bellman最適方程式はこのようになります.
\begin{eqnarray}
Q^*(s,a) &=& r + \gamma\underset{a'}{\max}{Q^{*}(s',a')} \\
&=& \underset{s'}{\mathbb{E}}\bigl[ \bigl. r+\gamma \underset{a'}{\max}{Q^{*}(s',a')} \bigr| s,a\bigr]
\end{eqnarray}
状態遷移が決定的な場合(単純な例)が1行目, 確率的な場合が2行目です.
価値ベース/方策ベース/モデルベース
強化学習アルゴリズムの特徴を表現するのに, 「価値ベース」「方策ベース」といった言葉をよく使います. 本記事ではこの概念に基づいてアルゴリズムを分類しました.
価値ベース(価値反復)のアルゴリズムでは, 最適価値関数$Q^{*}(s,a)$を学習し, そこから適当な方策(ε-グリーディー法やBoltzmann選択など)にしたがって行動を選択します.
**方策ベース(方策反復)**のアルゴリズムでは, 直接最適方策$\pi^{*}$を学習し, 割引報酬和を最大化します.
モデルベースのアルゴリズムは, マルコフ決定過程に関するパラメータ(状態遷移確率など)が既知で, 環境に関するモデルが構築できる場合に利用します. 構築したモデルに基づいて価値関数や方策関数を改善していくのですが, 多くの場合で環境のモデルを推定することは難しいので, 本記事では割愛します.
方策オン/オフ
また, 「方策オン型」「方策オフ型」といった言葉もよく使われます.
価値関数$Q(s,a)$の更新に用いるターゲット方策が, 実際の行動選択に用いる行動方策$\pi(a|s)$と一致している場合, そのアルゴリズムを方策オン型といい, 異なる場合は方策オフ型といいます.
言い換えると, Bellman方程式において$a'$を方策$\pi$によって選ぶ(右辺に$\pi$が含まれる)なら方策オン型, $\pi$とは別の方策によって選ぶ(右辺に$\pi$が含まれない)なら方策オフ型です.
方策オン型のアルゴリズムでは, Bellman方程式の解($Q(s,a)$の収束値)が方策に依存します.
一方, 方策オフ型のアルゴリズムでは, 解は方策に依存しませんが, 方策を変えると探索する領域が変わり収束速度が変化します.
Q学習とSARSAの比較をしてみるとわかりやすいです(後述).
価値ベースのアルゴリズム
価値ベースのアルゴリズムは大きく分けて, Q学習に基づくアプローチとSARSAに基づくアプローチの2種類が存在します.
両者はいずれも, 方策関数$\pi$を固定し, 価値関数$Q$のみを学習によって改善していきます.
異なる点は価値関数を更新する式のみです.
Q学習系
Q学習では, TD誤差に基づいて次のように価値関数$Q$を更新します. $\alpha$は学習率(ステップサイズ)です.
Q(s,a) \leftarrow Q(s,a) + \alpha (r + \gamma\underset{a'}{\max}{Q(s',a')} - Q(s,a))
更新式で実際に採用した行動$a'$を使っていない(方策に関わらず価値関数の最大値を与える行動を使っている)ので, 方策オフのTD学習であると言えます.
学習率がある条件を満たすとき, この価値関数は必ず収束することが証明されています(DQNのように近似器を用いる場合は別).
ちなみに, 価値関数が$w$を重みとするニューラルネットでモデリングされている場合は, 先ほど示したBellman最適方程式の右辺と左辺の差の2乘を損失関数として, 確率的勾配法などで最小化します.
L(w) = (r + \gamma\underset{a'}{\max}{Q(s',a'; w)} - Q(s,a; w))^2
損失関数が0になると, 価値関数はBellman最適方程式を満たし, したがって最適解が得られたことになります.
DQN
今説明したように, 価値関数をディープにしたものがDQN(deep Q-network)です.
しかし, それだけでは学習が難しいらしく, この手法のポイントは学習を成功させるための経験再生という工夫にあります.
普通に強化学習を行う場合, エージェントが得られるサンプル($s,a,r$)は時系列的に強い相関を持っています.
サンプル間の相関は深層学習において悪影響を及ぼすため, エージェントはサンプルをバッファにためておき, そこから複数のサンプルを取り出してミニバッチ学習を行います.
この経験再生という仕組みによって, サンプル間の相関を軽減することができます.
また, 損失関数の計算の際, ターゲット関数(Bellman最適方程式の右辺)の重みは過去の重み$w^-$でしばらくの間固定します.
L(w) = (r + \gamma\underset{a'}{\max}{Q(s',a'; w^-)} - Q(s,a; w))^2
これによってターゲット関数が学習の度に大きく変化しなくなり, 教師あり学習に近い安定した学習ができるようになります.
優先度付き経験再生
DQNの経験再生において, サンプルを損失関数が大きくなるものから順に取り出します.
苦手な分野を重点的に学習させる効果があります.
デュエリングネットワーク
価値関数$Q(s,a)$を, 行動に依存しない状態価値関数$V(s)$と, 依存するアドバンテージ関数$A(s,a)$に分けて学習させます.
Q(s,a) = V(s)+A(s,a)
DoubleDQN
通常のDQNではターゲット関数を最大値で作っているため, 実際よりも大きい値に偏ってしまいます.
この対策として, DoubleDQNでは, 今の重み$w'$から選ばれた行動$a'$を直前の重み$w$で評価します.
L(w) = (r + \gamma Q(s',\underset{a'}{\mathrm{argmax}}Q(s',a';w'); w) - Q(s,a; w))^2
いろいろとDQNのオプションを紹介しましたが, 「全部乗せ」で性能がよくなるというのがRainbowです.
画像は, Atari 2600というゲームのスコアを人との比でプロットしたものです.
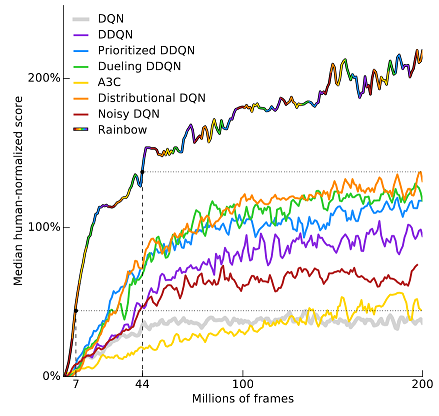
Rainbow: Combining Improvements in Deep Reinforcement Learning
Gorila
general reinforcement learning architectureの略で, DQNを分散処理によって高速化したアルゴリズムです.
Googleのレコメンドエンジンにも使われているそうです.
後で紹介するA3Cという有名なアルゴリズムの元となっています. 以降の手法では分散処理による高速化が主流となります.
Ape-X
優先度付き経験再生を分散処理で高速化したアルゴリズムです.
DQN版の他に決定方策勾配法(DPG)版もあります.
Atariのスコアが人の約4倍だそうです. すごいですね.
 [Distributed Prioritized Experience Replay](https://arxiv.org/abs/1803.00933)
[Distributed Prioritized Experience Replay](https://arxiv.org/abs/1803.00933)
R2D2 (2018年最新)
R2D2はrecurrent replay distributed DQNの略で, LSTMと経験再生と分散学習を組み合わせたアルゴリズムです.
データの順番を変えてしまう経験再生とLSTMはこれまで相性が悪いとされてきましたが, R2D2はこれを解決しました.
そして, 気になるAtariのスコアは…
人の13倍!!?すごすぎます.
Ape-Xを大きく上回るパフォーマンスを出しており, ファンシーな名前に負けていないのがすごいです.
ICLR 2019でまだレビュー中の最新手法です.
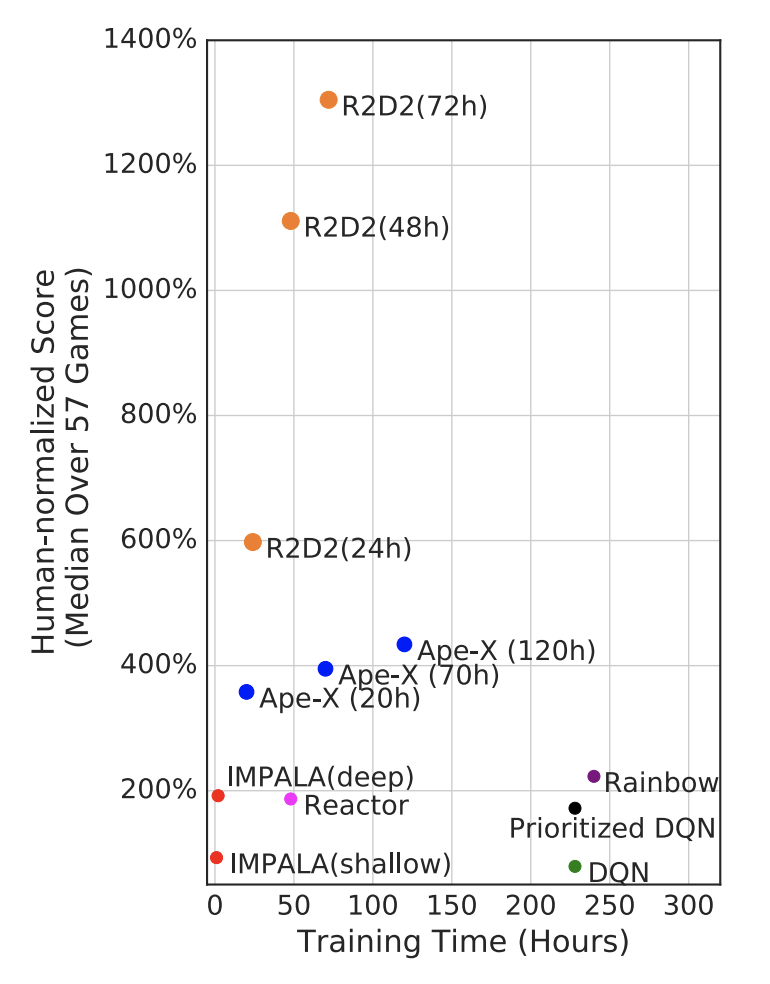
Recurrent Experience Replay in Distributed Reinforcement Learning
SARSA
基本的な方針はQ学習と同じで, 価値関数$Q$の更新式のみが異なります.
Q(s,a) \leftarrow Q(s,a) + \alpha (r + \gamma Q(s',a') - Q(s,a))
これは, 更新式で実際に採用した行動$a'$を使っているので, 方策オンのTD学習であると言えます.
Q学習と比べると, 収束が遅い一方で局所解に陥りにくいとされています.
更新式に$s,a,r,s',a'$が含まれることからSARSAと名付けられました.
原理的には以下のような損失関数を設計して, Deep SARSAなるアルゴリズムも考えられそうです.
L(w) = (r + \gamma Q(s',a'; w) - Q(s,a; w))^2
しかし, 方策オン型のアルゴリズムで経験再生を使おうとすると, バッファからサンプルした行動$a'$を選んだ(過去の)行動方策と更新したい(今の)ターゲット方策が異なるために上手くいきません.
したがって, 経験再生を利用できずサンプルが使い捨てになるという問題があります.
それでディープなSARSAのアルゴリズムは学習が難しいのか, 調べてもあまり見つかりませんでした.
方策ベースのアルゴリズム
方策ベースのアルゴリズムは, 方策関数$\pi$を直接改善する点が特徴です.
本来, 強化学習で本質的なのは状態価値や行動価値ではなく方策です.
その説明として, Lapanの本[6]では, 森の中で虎と遭遇したときの例が挙げられていました(以下抄訳).
〈逃げる〉〈隠れる〉〈バッグを投げつける〉といった選択肢が考えられるが, 「〈逃げる〉の価値はどのくらいだろうか?そしてその価値は〈何もしない〉より高いだろうか?」などと考えるのは馬鹿げている. 価値など気にせず, 素早く行動を決めるだけだ.
実際, 選択肢が無数にある場合は, 価値を最大にする行動を選ぶだけでも大変ですし, その分メモリを消費してしまうという実装上の問題もあります.
したがって, OpenAI GymのMuJoCoやロボット制御のように, 行動空間が連続な場合や多変数の場合には方策ベースの手法が使われます.
方策勾配法系(非Actor-Critic)
方策勾配法は, $\theta$をパラメータとする方策$\pi_{\theta}$に対して期待収益$J(\theta)$を確率的勾配法などで最大化します.
\begin{eqnarray}
\theta &\leftarrow& \theta + \alpha \nabla_{\theta}J(\theta)\\
where ~ J(\theta) &=& V^{\pi_{\theta}}(s_t) \\
&=& \sum_{a}{\pi_{\theta}(a|s)Q^{\pi_{\theta}}(s,a)}
\end{eqnarray}
学習をしていく過程で, 期待収益を高めるような行動は出やすく, 低くするような行動は出にくくなります.
ちなみに, 期待収益$J(\theta)$は符号を逆にすると分類モデルにおける交差エントロピーと同じ形になります.
方策関数$\pi_{\theta}(a|s)$は予測ラベル(確率分布)と, 価値関数$Q^{\pi_{\theta}}(s,a)$は教師ラベル(one-hotなベクトル)と対応しています.
また, 次の方策勾配定理が成り立ちます(証明略).
\begin{eqnarray}
\nabla_{\theta}J(\theta) &=& \mathbb{E}\Bigl[ \frac{\partial\pi_{\theta}(a|s)}{\partial\theta}\frac{1}{\pi_{\theta}(a|s)}Q^{\pi_{\theta}}(s,a) \Bigr]\\
&=& \mathbb{E}\Bigl[ \nabla_{\theta}\log{\pi_{\theta}}(a|s)~Q^{\pi_{\theta}}(s,a) \Bigr]
\end{eqnarray}
以上が方策勾配法の基礎です.
本節では方策ベースのアルゴリズムの中でもActor-Criticを用いないものについて紹介します.
'Vanilla' Policy Gradient
上記の方策勾配定理では, 式の中に$Q^{\pi_{\theta}}(s,a)$が含まれていました.
しかし, 先に述べたように, 広大な行動空間に対して価値関数を適切に設計することは難しいです.
そこで, 'Vanilla' Policy Gradient(方策勾配法にも派生がいろいろありますが, そのうちの元祖)では, 実際に得られた報酬の合計で$Q^{\pi_{\theta}}(s,a)$を近似します.
ステップ$t$から得られた報酬を$r_t$とおくと, 次のようになります.
\nabla_{\theta}J(\theta)\approx \sum_{t=t}^{T}\nabla_{\theta}\log\pi_{\theta}(a_t|s_t)~r_t
しかし, このままだと推定値の分散が大きく学習を阻害してしまうので, ベースライン除去というテクニックを用いて, 期待値をそのままに分散を小さくします.
\nabla_{\theta}J(\theta)\approx \sum_{t=t}^{T}\nabla_{\theta}\log\pi_{\theta}(a_t|s_t)~(r_t-b(s_t))
ベースライン$b(s_t)$は, 報酬との二乗誤差が最小になるようにステップごとに調節されます.
REINFORCE
REINFORCEというアルゴリズムでは, $T$ステップからなる試行を$M$エピソード行って得られた報酬の平均で$Q^{\pi_{\theta}}(s,a)$を近似します.
ベースライン$b$としては, 報酬の平均がよく用いられます.
$m$番目のエピソードの$t$ステップ目から得られた報酬を$r_{m,t}$とおくと, 次のようになります.
\begin{eqnarray}
\nabla_{\theta}J(\theta) &\approx& \frac{1}{M}\sum_{m=1}^{M}\frac{1}{T}\sum_{t=1}^{T}\nabla_{\theta}\log\pi_{\theta}(a_{m,t}|s_{m,t})~(r_{m,t}-b)\\
where~ b &=& \frac{1}{M}\sum_{m=1}^{M}\frac{1}{T}\sum_{t=1}^{T}r_{m,t}
\end{eqnarray}
$T$はエピソードごとに異なっていても大丈夫です.
ちなみに, REINFORCEはAlphaGoのRLポリシーネットワークを学習させるのにも利用されています.
Actor-Critic系
REINFORCEでは価値関数$Q$を実際の報酬の平均で近似し, 特に学習を行うことはありませんでした.
一方, 行動を決めるActor(行動器)を直接改善しながら, 方策を評価するCritic(評価器)も同時に学習させるのが, Actor-Criticのアプローチです.
一般に, Actor-Criticを用いると報酬のブレに惑わされにくくなり, 学習を安定して速くすることができます.
なお, 便宜上, 方策勾配法とActor-Criticを分けて書きましたが, これらは対になるような関係ではありません.
むしろ, Actorの学習には多くの場合方策勾配法が使われます.
強化学習はこういうところがつまずきポイントですね.
A3C
**A3C (asynchronous advantage Actor-Critic)**は'Vanilla' Policy Gradientとよく似ていますが, 大きく異なるのは次の3点です
- ベースライン$b(s)$をニューラルネットのCriticとする
- 期待収益$J$にエントロピー項を加える
- 分散非同期処理により学習を高速化
まず1点目についてです.
ベースラインを, 状態価値関数$V_{\phi}(s)$であると考えて$\phi$を重みとするニューラルネットでモデリングします.
このニューラルネットは多くの場合, 方策関数$\pi_{\theta}(a|s)$とネットワークの一部を共有させます.
いま, 報酬が価値関数$Q^{\pi_{\theta}}$の近似であることと, デュエリングネットワークで定義したアドバンテージ関数を思い出すと, 次の式のようになります.
\begin{eqnarray}
\nabla_{\theta}J(\theta, \phi) &\approx& \nabla_{\theta}\log\pi_{\theta}(a|s)~A(s,a)\\
where ~A(s,a) &=& Q^{\pi_{\theta}}(s,a)-V_{\phi}(s)
\end{eqnarray}
$Q^{\pi_{\theta}}$の近似としては, 1ステップ後の報酬でも$T$ステップ後までの割引報酬和でも使えます.
遠くまで先読みをするとREINFORCEに近くなります.
そして, $A(s,a)$の二乗が最小になるように重み$\phi$を更新していきます.
2点目についてです.
方策が決定的になるとCriticの学習がうまくいきません.
これを防ぐために, 期待収益$J$に$\pi_{\theta}(a|s)$のエントロピーを加えて次のように定義します(1ステップ先読みの場合).
\nabla_{\theta}J(\theta, \phi)\approx \nabla_{\theta}\log\pi_{\theta}(a|s)~(r-V_{\phi}(s))-\beta\sum_{a}{}\pi_{\theta}(a|s)\log{\pi_{\theta}(a|s)}
$\beta(>0)$は適当な係数です.
3点目についてです.
一定間隔で重みを共有しつつ分散非同期で学習することで, 学習の効率を高めています.
これによってCPU(マルチスレッド)でも学習ができるようになりました.
経験再生を使っていないので方策にRNNを使うことができます.
A3Cの後に, 分散同期にした**A2C (advantage Actor-Critic)**というアルゴリズムも提案されました.
DDPG
**DDPG (deep deterministic policy gradient; 深層決定方策勾配法)**は, Actor-Criticの枠組みで決定的な方策勾配法とDQNを組み合わせたアルゴリズムです.
行動空間が連続なときに使います.
まず, 行動は決定的な方策関数$\mu_{\theta}(s)$の出力とノイズ$N$の和で定義します.
a = \mu_{\theta}(s)+N
価値関数を$\phi$を重みとするニューラルネット$Q_{\phi}$で定義すると, 期待収益は次の式で表されます.
J_{\mathrm{DDPG}}(\theta) = Q_{\phi}^{\mu_{\theta}}(s,a)
これを$\theta$で偏微分した勾配は, 連鎖律を用いて次のように表せます.
\begin{eqnarray}
\nabla_{\theta}J_{\mathrm{DDPG}}(\theta) &=& \nabla_{\theta}Q_{\phi}^{\mu_{\theta}}(s,a)\\
&=& \nabla_{\theta}a ~ \nabla_a Q_{\phi}^{\mu_{\theta}}(s,a)\\
&=& \nabla_{\theta}\mu_{\theta}(s) ~ \nabla_a Q_{\phi}^{\mu_{\theta}}(s,a)
\end{eqnarray}
この勾配$\nabla_{\theta}J_{\mathrm{DDPG}}(\theta)$に従って, 方策関数$\mu_{\theta}(s)$の重みを更新します.
決定方策を採用したため, 行動空間が広大でも比較的少ないサンプルで勾配を計算できるらしいです.
価値関数$Q_{\phi}(s,a)$はDQNと同様に, 経験再生とターゲット関数を用いて次の損失関数を最小化するように重みを更新していきます.
L(\phi) = (r + \gamma\underset{a'}{\max}{Q_{\phi^-}(s',a')} - Q_{\phi}(s,a))^2
ただし, どちらのニューラルネットも重みの更新はソフトアップデートで行います.
すなわち, パラメータ$\tau(\ll 1)$に対して, 次のように更新します.
\begin{eqnarray}
\theta' &\leftarrow& \tau\theta+(1-\tau)\theta'\\
\phi' &\leftarrow& \tau\phi+(1-\tau)\phi'
\end{eqnarray}
TRPO
強化学習では, 1度方策関数が劣化するとその後で報酬が得られなくなり, その後の改善が困難になるという問題があります.
したがって, ニューラルネットの重みは慎重に更新する必要があります.
これを実現するために, **TRPO (trust region policy optimization)**では, 更新前後の重みのKLダイバージェンスに制約を設けます(trust region; 信頼領域).
式も確認しておきましょう.
まず, 更新後の重みを$\theta'$としたとき, 更新前後の方策関数の出力の比を$r(\theta;s,a)$とします(報酬とは関係ありません).
r(\theta;s,a) = \frac{\pi_{\theta}(a|s)}{\pi_{\theta'}(a|s)}
すると, 最適化の式は次のようになります.
\begin{eqnarray}
maximize ~J_{\mathrm{TRPO}}(\theta) = \underset{s,a}{\mathbb{E}}\bigl[ r(\theta;s,a)A_{\theta}(s,a) \bigr] \\
subject ~to~ \underset{s}{\mathbb{E}}\bigl[ D_{\mathrm{KL}}(\pi_{\theta}(a|s)||\pi_{\theta'}(a|s)) \bigr] \leq \delta
\end{eqnarray}
PPO
TRPOに対して, **PPO (proximal policy optimization)**は, 別のアプローチで制約を設けて計算量を削減しました.
PPOでは, 次のように$r(\theta;s,a)$を$\mathrm{clip}$関数により$[1-\epsilon,1+\epsilon]$の間に収めます.
さらに, クリップする前の目的関数と比較して最小値を取ることで, 大きな報酬につられて大胆な重み更新をしないようにしています.
maximize ~J_{\mathrm{PPO}}(\theta) = \underset{s,a}{\mathbb{E}}\bigl[ \min{(~r(\theta;s,a)A_{\theta}(s,a)}~,~ \mathrm{clip}(r(\theta;s,a),1-\epsilon,1+\epsilon)A_{\theta}(s,a) ~) \bigr]
MuJoCoの複数の環境で試したところ, 多くの場合でPPOが良い成績を出しました.
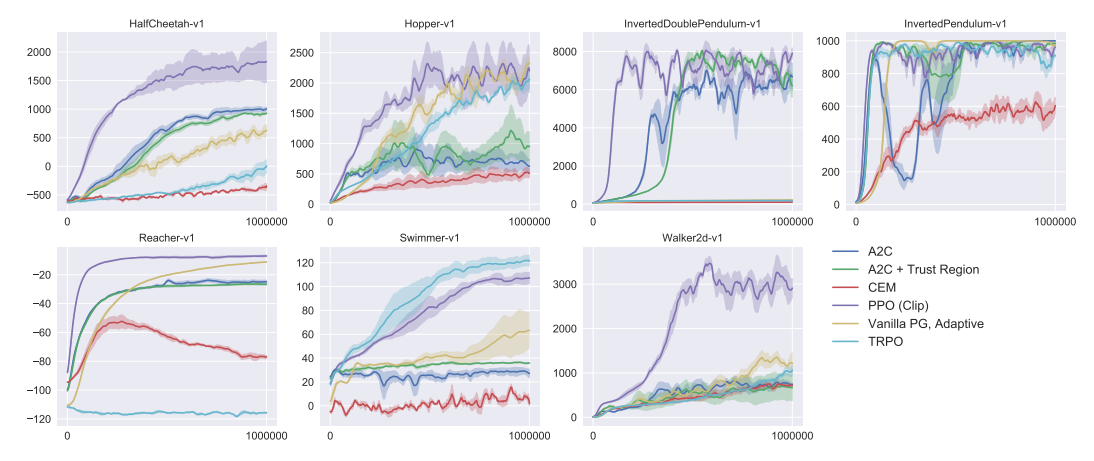
Proximal Policy Optimization Algorithms
ACER
**ACER (Actor Critic with experience replay)**は, A3Cを方策オフ型に書き換えて, 経験再生を利用するアルゴリズムです.
UNREAL
**UNREAL (unsupervised reinforcement and auxiliary learning; 教師なし強化補助学習)**は, A3Cに補助タスクを組み込んだもので, 3次元の迷路において好成績を収めたと報告されています.
補助タスクとして以下の3つを同時に学習させます.
- pixel control: 画像が大きく変化する動きを学習
- value function replay: 状態価値関数$V(s)$の学習において, 過去のデータをシャッフルさせて学習できるようにする
- reward prediction: 現在の状態から将来の報酬を予測させる
NAC
NAC (natural Actor-Critic)は, これまでユークリッド距離で定めていた方策勾配として, KLダイバージェンス(擬距離)で定めた自然勾配を用いたActor-Criticです.
自然勾配は通常の勾配に方策関数のフィッシャー情報量$F(\theta)$の逆行列をかけることで求められます.
\begin{eqnarray}
\tilde{\nabla}_{\theta} J(\theta) &=& F^{-1}(\theta)\nabla_{\theta} J(\theta)\\
where~ F(\theta) &=& \mathbb{E}\Bigl[ \nabla_{\theta}\log{\pi_{\theta}}(a|s)~ \nabla_{\theta}\log{\pi_{\theta}}(a|s)^{\mathrm{T}} \Bigr]
\end{eqnarray}
「なぜ自然勾配を用いるといいのか」という疑問に答えるのはおそらく難しく, 情報幾何などを学ぶ必要が出てくるでしょう.
おわりに
まとめ
これらを理解した上でもう一度, 価値ベースの手法と方策ベースの手法を比べてみましょう. 次のようなことがわかると思います.
| 価値ベース | 方策ベース | |
|---|---|---|
| 最適化の対象 | 価値関数 | 方策関数 |
| 最適化アルゴリズム | Q学習かSARSA | 確率的勾配降下法など |
| 利点 | 任意の方策で探索できる | 行動空間が広くても学習できる |
| 欠点 | 行動空間が広いと学習が難しい. メモリが必要 | モデルが劣化した後の復帰が難しい |
おまけ
調べていたらこんなジョークを見つけました. 実環境への早期の応用が望まれます.
Coworker on RL research: "We were supposed to make AI do all the work and we play games but we do all the work and the AI is playing games!"
— Andrej Karpathy (@karpathy) 2016年10月7日
あと, こんな「強化学習あるある」もあります.

Deep Reinforcement Learning Doesn't Work Yet
まじめな話
いろいろ深層強化学習のアルゴリズムを紹介しましたが, 上の画像のように, 最新のアルゴリズムでも実問題に適用してみるとうまく学習できないことがよくあります.
私の(深くない)経験に基づくと, 実問題ではアルゴリズムの選択よりも(状態, 行動, 報酬)の設計が重要になると思っています.
学習がうまくいかないときは, 次のような点について問題を切り分けて考えてみるといいかもしれません.
- 状態: 行動を選択するに足る状態が観測できているか(前処理でノイズを減らす, 特徴量を変える, ハードウェアならセンサの数を増やすなど)
- 行動: 行動選択に適切なモデルを設定しているか(多変数なら適切なモデルを設定して変数を減らすなど)
- 報酬: 報酬を適切に獲得できているか(報酬が0なら探索の幅を広げる, 報酬のハードルを下げて問題を簡単にする, 報酬の設計が逆強化学習など)
長くなりましたが, 最後までお読みいただきありがとうございました!
次は何かしらの問題に適用してみたいと思います!
参考文献
[1] Tutorial: Deep Reinforcement Learning, D. Silver.
YouTubeの講義は長いので, 概要を掴むならこちらがおすすめです.
[3] これから強化学習を勉強する人のための「強化学習アルゴリズム・マップ」と, 実装例まとめ - Qiita
アルゴリズム・マップのアイディアを参考にさせていただきました.
[3] Reinforcement Learning, R. S. Sutton and A. G. Barto, The MIT Press, 2018.
強化学習を網羅した定番の教科書です. オンラインの原著は邦訳に比べてかなり新しくなっているので, 原著で読みましょう.
近年の深層強化学習の動向を含めて大幅に改変された第2版が10月15日に出版されるそうです.
[4] ゼロから始める深層強化学習(NLP2018講演資料)/ Introduction of Deep Reinforcement Learning
PFNの前田さんと藤田さんによるスライドです.
[5] Policy Gradient Algorithms
方策ベースのアルゴリズムまとめです. 網羅的である上に, 論文やソースコードへのリンクも貼られていて便利です.
[6] Deep Reinforcement Learning Hands-On, M. Lapan, Puckt Publishing, 2018.
分厚い教科書です. ソースコードや応用例が詳しいです.
[7] 速習 強化学習―基礎理論とアルゴリズム― , C. Szepesvári 著, 小山田創哲 他訳, 共立出版, 2017.
「薄くてすぐに読めそう!」と思って勉強し始めの頃に読んでみたら, 数式を追えず挫折しました. 中級以上の方向けです.
[8] 強化学習その2
基礎から詳しく説明されています. 数式がごちゃごちゃしていて戸惑うかもしれませんが, その分丁寧です.
このシリーズの他のスライドもおすすめです.
[9] 強化学習についてまとめる
このシリーズも網羅的です.
[10] これからの強化学習, 牧野貴樹 他著, 森北出版, 2016.
日本語で基礎を学ぶなら, おそらくこれが一番わかりやすいです.