典型的な DP (動的計画法) のパターンを整理 Part 1 ～ ナップサック DP 編 ～

はじめに --- DP は役に立つ

はじめまして。NTTデータ数理システムでアルゴリズムを探求している大槻 (通称、けんちょん) です。
好きなアルゴリズムは最小カットやマッチングですが、会社ではなぜか「DP が好きな人」と呼ばれています。

巷ではよく「DP なんて実務では使わない」といった言説が定期的に流れますが、そんなことはないです。僕自身この 2 年間で DP が使える実務案件に 3 件くらい関わりました！

それはともかくとして、DP を学び立ての方がよく抱く悩みとして「バリエーションが多すぎて混乱するし、統一的なフレームワークがほしい」というのがあります。確かに DP のバリエーションは非常に多岐にわたるのですが、そのほとんどが以下の 3 つのフレームワークで説明できると思います:

• ナップサック DP
• 区間 DP
• bit DP

今回はこのうちのナップサック DP について、とにかく「習うより慣れろ」の精神で、これらのパターンの例題を幾つか解くことで、自然に典型的な DP の世界を俯瞰することを目指します。

1 ナップサック DP とは

まずはナップサック問題から...と言いたいところなのですが、最初はもっと簡単な問題を考えてみましょう。

問題 1:　最大和問題

$n$ 個の整数 $a[0], a[1], \dots, a[n-1]$ が与えられる。これらの整数から何個かの整数を選んで総和をとったときの、総和の最大値を求めよ。また、何も選ばない場合の総和は 0 であるものとする。

【制約】
・$1 \le n \le 10000$
・$-1000 \le a[i] \le 1000$

【数値例】
1)
**　$n = 3$**
**　$a = (7, -6, 9)$**
**　答え: 16 (7 と 9 を選べばよいです)**

2)
**　$n$ = 2**
**　$a = (-9, -16)$**
**　答え: 0 (何も選ばないのがよいです)**

---

はい、既にお気づきの方が多いと思いますが、これは DP を使うまでもなく「正の値を全部足す」だけでよいです。しかし、この問題を敢えて DP で書いてみることで DP に慣れようという企画です。

　
【解法】
$\rm{dp}[0]$ := 何も選ばない状態
$\rm{dp}[1]$ := 0 番目までの整数 ($a$[0] のみ) の中から整数を選んで総和をとったときの、総和の最大値
$\rm{dp}[2]$ := 1 番目までの整数 ($a[0], a[1]$) の中から整数を選んで総和をとったときの、総和の最大値
…
$\rm{dp}[i+1]$ := $i$ 番目までの整数 ($a[0], \dots, a[i]$) の中から整数を選んで総和をとったときの、総和の最大値
とします。
求める値は、$\rm{dp}[n]$ です。

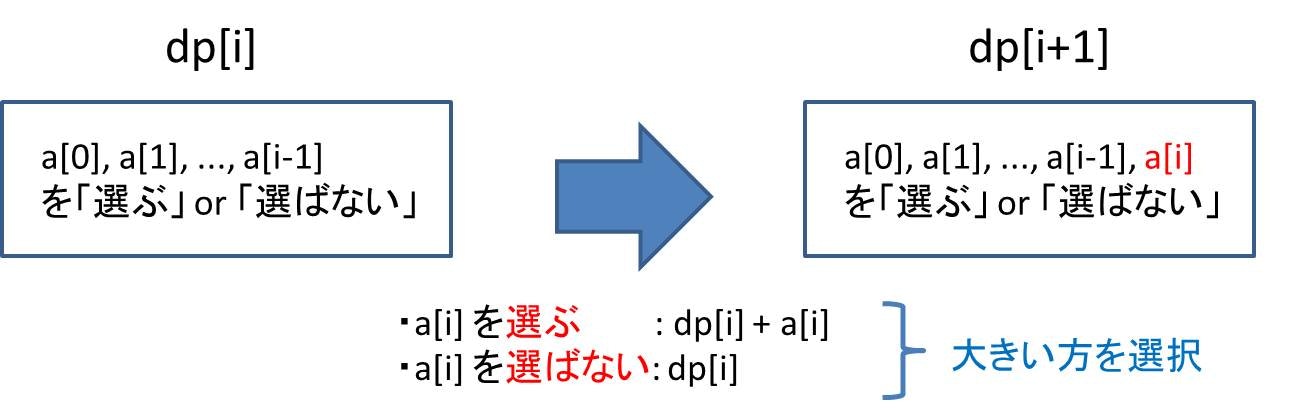
既に $\rm{dp}[i]$ の値が求まっていることを前提に、$\rm{dp}[i+1]$ の値を求めることを考えます。
$\rm{dp}[i]$ を使って $\rm{dp}[i+1]$ について考えるとき、$a[0], a[1], \dots, a[i-1]$ のどれを選んだらよいかが既に決まっているので、$a[i]$ を選ぶか選ばないかだけ決めればよいです。

• 選ぶとき　　: $\rm{dp}[i]$ に $a[i]$ が加算されるので、$\rm{dp}[i+1] = \rm{dp}[i] + a[i]$ です
• 選ばないとき: $\rm{dp}[i]$ は特に何も加算されないので、$\rm{dp}[i+1] = \rm{dp}[i]$ です

これらをまとめると、以下のようになります。

＜DP遷移式＞

$$\rm{dp}[i+1] = \max(\rm{dp}[i], \rm{dp}[i] + a[i])$$

数学で言うところの漸化式と一緒ですね。遷移していくためには、初期値が必要です。初期値は

＜初期値＞

$$\rm{dp}[0] = 0　(何も選んでいない初期状態)$$

です。あとは、以上のことをC++言語で書いてあげると、以下のようになります。

#include <iostream>
#include <algorithm>
using namespace std;

// 入力
int n;
int a[10010];  // 最大10000個ですが、少しだけ多めにとります

// DP テーブル
int dp[10010];


int main() {
	cin >> n;
	for (int i = 0; i < n; ++i) cin >> a[i];

	dp[0] = 0;
	for (int i = 0; i < n; ++i) {
		dp[i + 1] = max(dp[i], dp[i] + a[i]);
	}

	cout << dp[n] << endl;
}

さて、いよいよ次からナップサック問題を考えてみましょう。

2 ナップサック問題

ナップサック問題の登場までが長くなってしまいましたが、本来 DP 以外で簡単に解ける問題を敢えて DP で解いたのは、ナップサック問題に対する DP はこれよりも一段難易度が上がるからです。実際に解いてみましょう！
　

問題 2:　ナップサック問題

$n$ 個の品物があり、$i$ 番目の品物のそれぞれ重さと価値が $\rm{weight}[i], \rm{value}[i]$ となっている ($i = 0, 1, ..., n-1$)。
これらの品物から重さの総和が $W$ を超えないように選んだときの、価値の総和の最大値を求めよ。

【制約】
・$1 \le n \le 100$
・$\rm{weight}[i], \rm{value}[i]$ は整数
・$1 \le \rm{weight}[i], \rm{value}[i] \le 1000$
・$1 \le W \le 10000$

【数値例】
1)
**　$n = 6$**
**　$(\rm{weight},\rm{value}) = {(2,3), (1,2), (3,6), (2,1), (1,3), (5,85)}$**
**　$W = 9$**
**　答え: 94 ((3,6), (1,3), (5,85) を選んだときが最大です)**

---

さっきの問題が「価値」だけだったのに対し、「重さ」が加わった感じですね。基本的に、重さに対する価値の比率 $\rm{value}[i] / \rm{weight}[i]$ が大きいものを選んでいきたいわけですが、単に「$\rm{value}[i] / \rm{weight}[i]$ が大きい順にソートして、重さが $W$ を超えないギリギリまで詰める」という方針では最適解になるとは限らないです。上の数値例もその反例となっています。

　
【解法】
さっきと同じようにやります。しかし、完全にさっきと同じように

$\rm{dp}[i+1] := i$ 番目までの品物の中から重さが $W$ を超えないように選んだときの、価値の総和の最大値

としてしまうと詰まってしまいます。$\rm{dp}[i+1]$ を考えるときに、$\rm{dp}[i]$ に対して品物 $(\rm{weight}[i], \rm{value}[i])$ を加えるか否かを考えるわけだが、加えたときに重さが $W$ を超えてしまうのかどうかがわからないという問題が起こります。$\rm{dp}[i]$ に対して、「今重さがどうなっているか」という情報が必要なのです。そこで少し修正して以下のようにします:

$\rm{dp}[i+1][w]$ := $i$ 番目までの品物の中から重さが $w$ を超えないように選んだときの、価値の総和の最大値

そして先程は $\rm{dp}[i]$ の値が求まっていることを前提にして $\rm{dp}[i+1]$ の値を考えたわけですが、今回は $\rm{dp}[i][w]; (w = 0, 1, \dots, W)$ の値が求まっていることを前提にして、$\rm{dp}[i+1][w]; (w = 0, 1, \dots, W)$ の値を考えてみます。

$\rm{dp}[i+1][w]$ の値を求めるには、以下のうち大きい方をとります:

• 品物 $(\rm{weight}[i], \rm{value}[i])$ を選ぶ場合 ($w \ge \rm{weight}[i]$ の場合のみ)
  $$\rm{dp}[i+1][w] = \rm{dp}[i][w-\rm{weight}[i]] + \rm{value}[i]$$

• 品物 $(\rm{weight}[i], \rm{value}[i])$ を選ばない場合
  $$\rm{dp}[i+1][w] = \rm{dp}[i][w]$$

まとめると、以下のようになります。

＜DP漸化式＞

\rm{dp}[i+1][w] = \left\{
\begin{array}{ll}
\max (\rm{dp}[i][w-\rm{weight}[i]] + \rm{value}[i], \rm{dp}[i][w]) & (w \ge \rm{weight}[i]) \\
\rm{dp}[i][w] & (w < \rm{weight}[i])
\end{array}
\right.

<DP初期条件＞
$$\rm{dp}[0][w] = 0　(w = 0, 1, \dots, W)$$

「問題1: 最大和問題」に比べると、dp テーブルの添字が 1 個から 2 個に増えた分、少しだけ難易度が上がりました。実際に DP を設計するときに、「これだけじゃ情報が足りない -> 添字を付け足す」というのは非常によく行います。
これを素直に C++ で実装すると以下のようになります。

#include <iostream>
#include <climits>
#include <algorithm>
using namespace std;

// 入力
int n, W;
int weight[110], value[110];

// DPテーブル
int dp[110][10010];

int main() {
  cin >> n >> W;
  for (int i = 0; i < n; ++i) cin >> value[i] >> weight[i];

  // DP初期条件: dp[0][w] = 0
  for (int w = 0; w <= W; ++w) dp[0][w] = 0;

  // DPループ
  for (int i = 0; i < n; ++i) {
    for (int w = 0; w <= W; ++w) {
      if (w >= weight[i]) dp[i+1][w] = max(dp[i][w-weight[i]] + value[i], dp[i][w]);
      else dp[i+1][w] = dp[i][w];
    }
  }

  cout << dp[n][W] << endl;
}

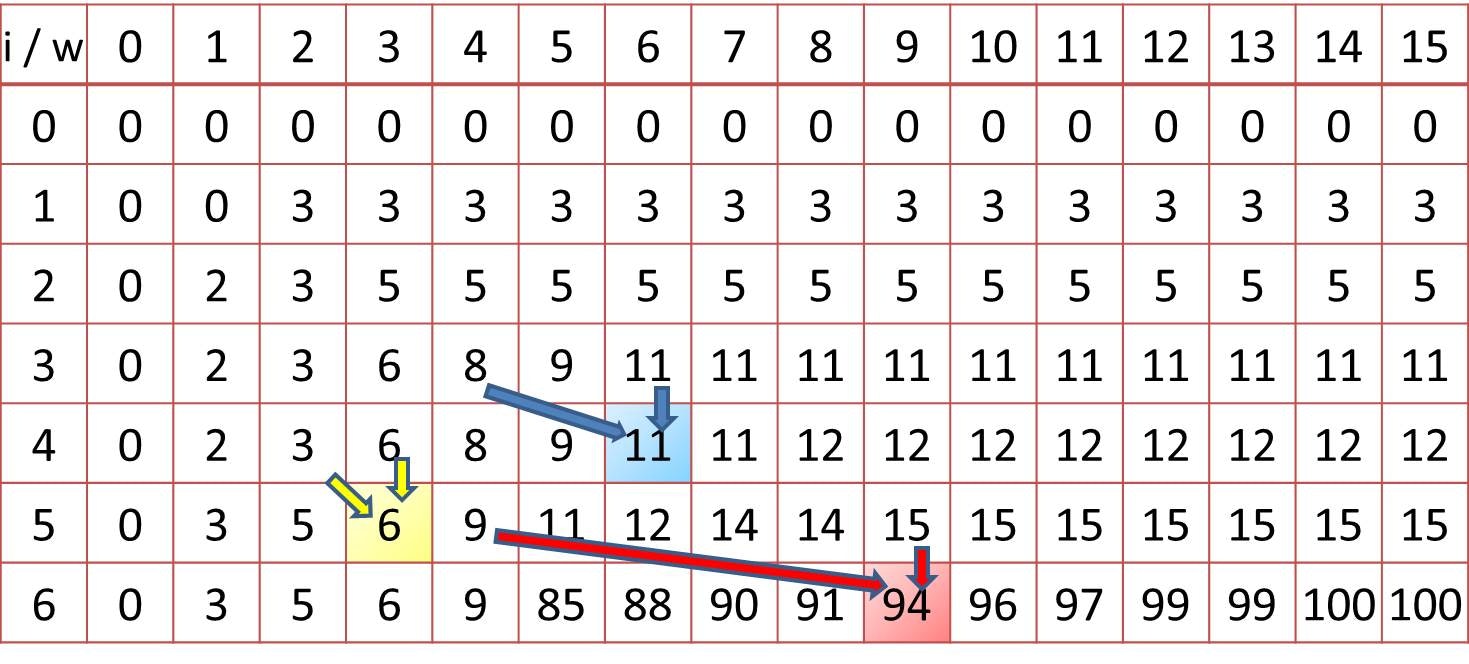
なお、このナップサック問題に対する DP について、実際にテーブル値が更新される様子は下図のようになります ($(\rm{weight},\rm{value}) = {(2,3), (1,2), (3,6), (2,1), (1,3), (5,85)}$ の場合)。

　
　

3 部分和問題とその応用たち

さて、DP で解ける問題は最適化問題だけではありません。ナップサック問題とよく似た問題として、次の部分和問題も有名です。むしろ、この部分和問題の方が簡単な問題です (部分和問題の方が簡単な問題で、部分和問題が NP-complete だから、ナップサック問題が NP-hard であることが示される、という話もあったりします)。
　

問題 3:　部分和問題

$n$ 個の正の整数 $a[0], a[1], \dots, a[n-1]$ と正の整数 $A$ が与えられる。これらの整数から何個かの整数を選んで総和が $A$ になるようにすることが可能か判定せよ。可能ならば "YES" と出力し、不可能ならば "NO" と出力せよ。

【制約】
・$1 \le n \le 100$
・$1 \le a[i] \le 1000$
・$1 \le A \le 10000$

【数値例】
1)
**　$n = 3$**
**　$a = (7, 5, 3)$**
**　$A = 10$**
**　答え: YES (7 と 3 を選べばよいです)**

2)
**　$n$ = 2**
**　$a = (9, 7)$**
**　$A = 6$**
**　答え: NO**

---

【解法】
ナップサック問題とほぼ一緒です。
$\rm{dp}[i+1][j]$ := $i$ 番目までの整数の中からいくつか選んで総和を $j$ とすることが可能かどうか (bool値)
として、$\rm{dp}[i][j]; (j = 0, 1, \dots, A)$ を使って $\rm{dp}[i+1][j]; (j = 0, 1, \dots, A)$ の値を更新することを考えます。

$\rm{dp}[i+1][j]$ の値を求めるには、以下のようになります。

• 整数 $a[i]$ を選ぶ場合 ($j \ge a[i]$ の場合のみ)
  $$\rm{dp}[i][j - a[i]]　が　\rm{True}　なら、\rm{dp}[i+1][j]　も　\rm{True}$$

• 整数 $a[i]$ を選ばない場合
  $$\rm{dp}[i][j]　が　\rm{True}　なら、\rm{dp}[i+1][j]　も　\rm{True}$$

まとめると、以下のようになります。

＜DP漸化式＞

\rm{dp}[i+1][j] = \left\{
\begin{array}{ll}
\rm{dp}[i][j - a[i]]　|　\rm{dp}[i][j] & (j \ge a[i]) \\
\rm{dp}[i][j] & (j < a[i])
\end{array}
\right.

<DP初期条件＞

\rm{dp}[0][j] = \left\{
\begin{array}{ll}
\rm{True} & (j = 0) \\
\rm{False} & (j \neq 0)
\end{array}
\right.

(0 個の整数の和は 0 とみなせるので、$\rm{dp}[0][0]$ のみ $\rm{True}$ です)

ここで、| は or 演算子です。ソースコードにすると、以下のようになります。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

// 入力
int n, A;
int a[110];

// DPテーブル
bool dp[110][10010];

int main() {
  cin >> n >> A;
  for (int i = 0; i < n; ++i) cin >> a[i];

  memset(dp, 0, sizeof(dp));   // 一旦すべて false に
  dp[0][0] = true;             // dp[0][0] だけ true に

  for (int i = 0; i < n; ++i) {
    for (int j = 0; j <= A; ++j) {
      dp[i+1][j] |= dp[i][j];
      if (j >= a[i]) dp[i+1][j] |= dp[i][j-a[i]];
    }
  }

  if (dp[n][A]) cout << "YES" << endl;
  else cout << "NO" << endl;
}

　

さて、この部分和問題は「A を作れますか？」という判定問題でしたが、DP はもう少し賢いこともできます。ちょっと賢くして「A を作る方法は何通りありますか？」という問題をやってみましょう！

問題 4:　部分和数え上げ問題

$n$ 個の正の整数 $a[0], a[1], \dots, a[n-1]$ と正の整数 $A$ が与えられる。これらの整数から何個かの整数を選んで総和が $A$ になるようにする方法が何通りあるかを求めよ。ただし、答えがとても大きくなる可能性があるので、1,000,000,009 で割った余りで出力せよ。

【制約】
・$1 \le n \le 100$
・$1 \le a[i] \le 1000$
・$1 \le A \le 10000$

【数値例】
1)
**　$n = 5$**
**　$a = (7, 5, 3, 1, 8)$**
**　$A = 12$**
**　答え: 2 ((7と5), (3と1と8) の 2 通りがあります)**

2)
**　$n = 4$**
**　$a = (4, 1, 1, 1)$**
**　$A = 5$**
**　答え: 3 ((4, 1), (4, 1), (4, 1) の 3 通りがあります。同じ 1 でも index が違うものは異なる組合わせとみなします)**

---

部分和問題にほんの少しの変更を付け加えるだけです。
$\rm{dp}[i+1][j]$ := $i$ 番目までの整数の中からいくつか選んで総和を $j$ とする場合の数
として、$\rm{dp}[i+1][j]$ の値を求めるには、以下の 2 つの場合を加算します。

• 整数 $a[i]$ を選ぶ場合 ($j \ge a[i]$ の場合のみ)
  $$\rm{dp}[i][j - a[i]] 通り$$

• 整数 $a[i]$ を選ばない場合
  $$\rm{dp}[i][j] 通り$$

まとめると、以下のようになります。

＜DP漸化式＞

\rm{dp}[i+1][j] = \left\{
\begin{array}{ll}
\rm{dp}[i][j - a[i]] + \rm{dp}[i][j] & (j \ge a[i]) \\
\rm{dp}[i][j] & (j < a[i])
\end{array}
\right.

<DP初期条件＞

\rm{dp}[0][j] = \left\{
\begin{array}{ll}
1 & (j = 0) \\
0 & (j \neq 0)
\end{array}
\right.

(0 個の整数の和は 0 とみなせるので、$\rm{dp}[0][0]$ のみ 1 通りです)

ソースコードにすると以下の通りです。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int MOD = 1000000009;

// 入力
int n, A;
int a[110];

// DPテーブル
int dp[110][10010];

int main() {
  cin >> n >> A;
  for (int i = 0; i < n; ++i) cin >> a[i];

  memset(dp, 0, sizeof(dp));   // 一旦すべて 0 に
  dp[0][0] = 1;                // dp[0][0] だけ 1 に

  for (int i = 0; i < n; ++i) {
    for (int j = 0; j <= A; ++j) {
      (dp[i+1][j] += dp[i][j]) %= MOD;
      if (j >= a[i]) (dp[i+1][j] += dp[i][j-a[i]]) %= MOD;
    }
  }

  cout << dp[n][A] << endl;
}

　

さらに、以下のような問題も考えられます。

問題 5:　最小個数部分和問題

$n$ 個の正の整数 $a[0], a[1], \dots, a[n-1]$ と正の整数 $A$ が与えられる。これらの整数から何個かの整数を選んで総和が $A$ にする方法をすべて考えた時、選ぶ整数の個数の最小値を求めよ。$A$ にすることができない場合は -1 と出力せよ。

【制約】
・$1 \le n \le 100$
・$1 \le a[i] \le 1000$
・$1 \le A \le 10000$

【数値例】
1)
**　$n = 5$**
**　$a = (7, 5, 3, 1, 8)$**
**　$A = 12$**
**　答え: 2 ((7, 5)と(3, 1, 8)とがありますが、(7, 5) の2個が最小です)**

2)
**　$n = 2$**
**　$a = (7, 5)$**
**　$A = 6$**
**　答え: -1**

---

　
【解法】

$\rm{dp}[i+1][j]$ := $i$ 番目までの整数の中からいくつかの整数を選んで総和が $j$ とする方法をすべて考えたときの、選んだ整数の個数の最小値

とすると、$\rm{dp}[i+1][j]$ の値を求めるには、以下の 2 つの場合の minimum をとります。

• 整数 $a[i]$ を選ぶ場合 ($j \ge a[i]$ の場合のみ)
  $$\rm{dp}[i][j - a[i]] + 1$$

• 整数 $a[i]$ を選ばない場合
  $$\rm{dp}[i][j]$$

まとめると、以下のようになります。

＜DP漸化式＞

\rm{dp}[i+1][j] = \left\{
\begin{array}{ll}
\min(\rm{dp}[i][j - a[i]] + 1, \rm{dp}[i][j]) & (j \ge a[i]) \\
\rm{dp}[i][j] & (j < a[i])
\end{array}
\right.

<DP初期条件＞

\rm{dp}[0][j] = \left\{
\begin{array}{ll}
0 & (j = 0) \\
\infty & (j \neq 0)
\end{array}
\right.

(0 個の整数の和は 0 とみなせるので、$\rm{dp}[0][0]$ のみ 0 個です。)

ソースコードにすると、以下のようになります。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int INF = 1<<29;        // 十分大きい値にする, INT_MAX にしないのはオーバーフロー対策

// 入力
int n, A;
int a[110];

// DPテーブル
int dp[110][10010];

int main() {
  cin >> n >> A;
  for (int i = 0; i < n; ++i) cin >> a[i];

  // 一旦すべて INF に
  for (int i = 0; i < 110; ++i) for (int j = 0; j < 10010; ++j) dp[i][j] = INF;
  dp[0][0] = 0;                // dp[0][0] だけ 0 に

  for (int i = 0; i < n; ++i) {
    for (int j = 0; j <= A; ++j) {
      dp[i+1][j] = min(dp[i+1][j], dp[i][j]);
      if (j >= a[i]) dp[i+1][j] = min(dp[i+1][j], dp[i][j-a[i]] + 1);
    }
  }

  if (dp[n][A] < INF) cout << dp[n][A] << endl;
  else cout << -1 << endl;
}

　

最後に、発展問題として、以下の問題を考えてみましょう。重要な教訓が1つ得られる問題です。

問題 6:　K個以内部分和問題

$n$ 個の正の整数 $a[0], a[1], \dots, a[n-1]$ と正の整数 $A$ が与えられる。これらの整数から $K$ 個以内の整数を選んで総和が $A$ になるようにすることが可能か判定せよ。可能ならば "YES" と出力し、不可能ならば "NO" と出力せよ。

【制約】
・$1 \le K \le n \le 500$
・$1 \le a[i] \le 1000$
・$1 \le A \le 10000$

【数値例】
1)
**　$n = 3$**
**　$K = 2$**
**　$a = (7, 5, 3)$**
**　$A = 10$**
**　答え: YES (7 と 3 を選べばよいです)**

2)
**　$n = 3$**
**　$K = 1$**
**　$a = (7, 5, 3)$**
**　$A = 10$**
**　答え: NO**

---

【解法】
問題3 (部分和問題) に対して、$K$ 個以内という制約が加わりました。問題3 のように

$\rm{dp}[i+1][j]$ := $i$ 番目までの整数の中からいくつか選んで総和を $j$ とすることが可能かどうか

として、$\rm{dp}[i][j]$ を使って $\rm{dp}[i+1][j]$ の値を更新することを考えると、既に何個選んだかの情報がないので $a[i]$ を選ぶことにしたときに $K$ 個を超えてしまうかどうかがわかりません。そこで、次のようにしたくなります。このように添字を付け加えて DP を設計すること自体はとても重要なテクニックです。

$\rm{dp}[i+1][j][k]$ := $i$ 番目までの整数の中から $k$ 個の整数を選んで足した総和が $j$ とすることが可能かどうか

こうすることで、確かにこの問題を解くことのできるアルゴリズムを構成することができます。しかし、このとき計算時間はどのようになるでしょうか。DP テーブルのサイズは、$nKA$ となり、実際のアルゴリズムの計算時間も $O(nKA)$ となります。もしこのオーダーで間に合うような制約であればいいのですが、今回はこれでは間に合いません。そこで、「DP の添字ではなく、DP の値そのものに情報をもたせられないか」と考えてみましょう。プログラミングコンテストチャレンジブック第二版 P.63にもある通り、一般に bool 値を求める DP をすることは無駄であることが多く、同じ計算量でもっと多くのことを知ることができます。
具体的には次のようにしてみましょう。

$\rm{dp}[i+1][j]$ := $i$ 番目までの整数の中からいくつかの整数を選んで総和が $j$ とする方法をすべて考えたときの、選んだ整数の個数の最小値

これは実は問題 5 (最小個数部分和問題) で立てる DP そのものですね。問題 5 と同じようにテーブルを作っておけば、最後答えを出力するときに

• $\rm{dp}[n][A] \le K$ ならば "YES"
• $\rm{dp}[n][A] > K$ ならば "NO"

とすればよいです。これならば計算時間オーダーは、$O(NA)$ で求めることができます。

このテクニックを推し進めると、以下の問題もオーダー $O(NA)$ で解くことができます。解説はプログラミングコンテストチャレンジブック第二版 P.62～P.63にありますので、是非考えてみると面白いと思います。

問題 7:　個数制限付き部分和問題

$n$ 種類の正の整数 $a[0], a[1], \dots, a[n-1]$ がそれぞれ $m[i]$ 個ずつある。また、正の整数 $A$ が与えられる。これらの整数からいくつか選んで総和が $A$ になるようにすることが可能か判定せよ。可能ならば "YES" と出力し、不可能ならば "NO" と出力せよ。

【制約】
・$1 \le n \le 500$
・$1 \le a[i], m[i] \le 10000$
・$1 \le A \le 10000$

---

　
　

4 二次元ナップサック DP --- 弾性マッチングやdiffコマンドの仕組みなど

ここまで「1個前の DP 値の情報から、現在の DP 値を更新する」タイプのナップサック DP を見て来ましたが、今回は「時系列に沿って進んでいくインデックス」が 2 個になったものを見て行きます。次の最長共通部分列 (LCS) 問題は有名問題です。

問題 8:　最長共通部分列 (LCS) 問題

2つの文字列 $S$, $T$ が与えられる。"abcde" といった文字列の部分文字列とは、"a", "ad", "abe" といったように、文字列から文字を幾つか抜き出して順に繋げてできる文字列のことを言うものとする。このとき、$S$ と $T$ の共通の部分文字列となる文字列の長さの最大値を求めよ。

【制約】
・$1 \le |S|, |T| \le 1000$

【数値例】
1)
**　$S = $"abcde"**
**　$T = $"acbef"**
**　答え: 3 ("ace" が長さ最大です)**

2)
**　$S = $"pirikapirirara"**
**　$T = $"poporinapeperuto"**
**　答え: 6 ("ppriar" が長さ最大です)**

---

【解法】
$\rm{dp}[i+1][j+1]$ := $S$ の $i$ 文字目までと $T$ の $j$ 文字目まででの LCS の長さ
とします。

今までは、$\rm{dp}[i]$ を使って $\rm{dp}[i+1]$ を表したりしましたが、今回は $\rm{dp}[i][j]$, $\rm{dp}[i+1][j]$, $\rm{dp}[i][j+1]$ を使って $\rm{dp}[i+1][j+1]$ を表すことを考えると次のようになります。

• $S[i] == T[j]$ ならば、$\rm{dp}[i][j]$ に対して、共通の $S$ の $i$ 文字目と $T$ の $j$ 文字目を付け加えれば 1 文字伸びるので、
  $$\rm{dp}[i+1][j+1] = \rm{dp}[i][j] + 1$$

• $\rm{dp}[i+1][j]$ に対して、$T$ の $j$ 文字目を考慮しても特に LCS の長さは変わらず、
  $$\rm{dp}[i+1][j+1] = \rm{dp}[i+1][j]$$

• $\rm{dp}[i][j+1]$ に対して、$S$ の $i$ 文字目を考慮しても特に LCS の長さは変わらず、
  $$\rm{dp}[i+1][j+1] = \rm{dp}[i][j+1]$$

まとめると、

＜DP漸化式＞

\rm{dp}[i+1][j+1] = \left\{
\begin{array}{ll}
\max(\rm{dp}[i][j] + 1, \rm{dp}[i+1][j], \rm{dp}[i][j+1]) & (S[i] == T[j]) \\
\max(\rm{dp}[i+1][j], \rm{dp}[i][j+1]) & (S[i] != T[j])
\end{array}
\right.

＜DP初期条件＞
$$\rm{dp}[0][0] = 0$$

＜求める値＞
$$\rm{dp}[|S|][|T|]$$

このアルゴリズムの計算時間オーダーは、$O(|S||T|)$ になります。ソースコードにすると以下のようになるでしょう。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int INF = 1<<29;        // 十分大きい値にする

// 入力
string S, T;

// DP テーブル
int dp[1010][1010];

int main() {
  cin >> S >> T;

  memset(dp, 0, sizeof(dp));    // 初期化
  for (int i = 0; i < S.size(); ++i) {
    for (int j = 0; j < T.size(); ++j) {
      if (S[i] == T[j]) dp[i+1][j+1] = max(dp[i+1][j+1], dp[i][j] + 1);
      dp[i+1][j+1] = max(dp[i+1][j+1], dp[i+1][j]);
      dp[i+1][j+1] = max(dp[i+1][j+1], dp[i][j+1]);
    }
  }

  cout << dp[S.size()][T.size()] << endl;
}

　

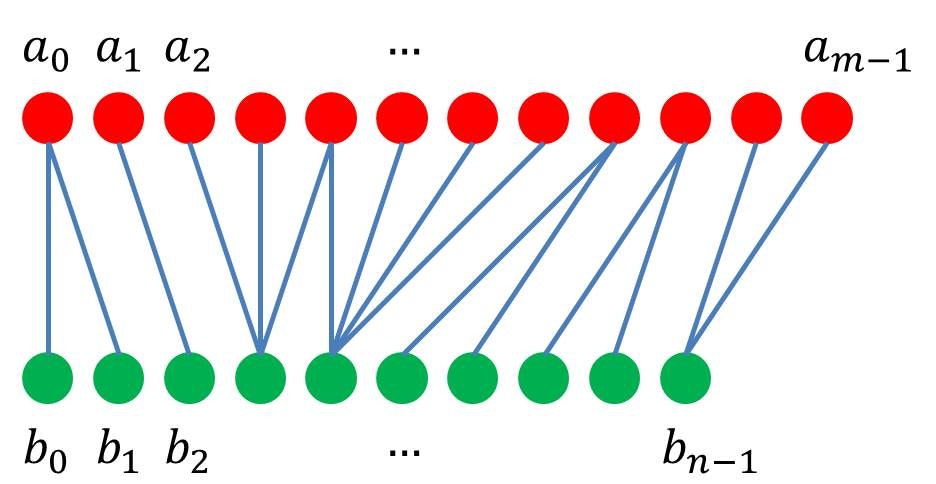
この最長共通部分列問題を少し発展させた最小コスト弾性マッチングと呼ばれる問題は、以下のイメージ図にあるように、2つの系列の間の対応する部分を順にマッチングさせていく手法で、パターン認識なども諸問題に応用のある重要な問題です。例えば、予め沢山の "トウキョウ" といった音声波形データを標本データとして蓄えておき、未知の音声波形データがどの単語を表しているかを推定する問題があげられます。このとき、未知の音声波形データと、各単語の標本データとの「近さ」を、最小コスト弾性マッチングの最適解によって測ることになります。

問題 9:　最小コスト弾性マッチング問題

系列 $A = (a_0, a_1, \dots, a_{m-1})$, $B = (b_0, b_1, \dots, b_{n-1})$ が与えられる。各ペア $(a_i, b_j)$ をマッチさせたときのコストは $c(i, j)$ で与えられる。最小コスト弾性マッチングを求めよ。

【制約】
・$1 \le m, n \le 1000$

---

【解法】
$\rm{dp}[i+1][j+1]$ := $a_i$ までと $b_j$ まででの弾性マッチングの最小コスト
とします。

$\rm{dp}[i][j]$, $\rm{dp}[i+1][j]$, $\rm{dp}[i][j+1]$ を使って $\rm{dp}[i+1][j+1]$ を表すことを考えると次のようになります。

• $\rm{dp}[i][j]$ に対して、新たにペア $(a[i], b[j])$ をマッチさせて
  $$\rm{dp}[i+1][j+1] = \rm{dp}[i][j] + c(i, j)$$

• $\rm{dp}[i+1][j]$ に対して、新たにペア $(a[i], b[j])$ をマッチさせて
  $$\rm{dp}[i+1][j+1] = \rm{dp}[i+1][j] + c(i, j)$$

• $\rm{dp}[i][j+1]$ に対して、新たにペア $(a[i], b[j])$ をマッチさせて
  $$\rm{dp}[i+1][j+1] = \rm{dp}[i][j+1] + c(i, j)$$

まとめると、

＜DP漸化式＞

$$\rm{dp}[i+1][j+1] = \min(\rm{dp}[i][j], \rm{dp}[i+1][j], \rm{dp}[i][j+1]) + c(i, j)$$

＜DP初期条件＞
$$\rm{dp}[0][0] = 0$$

＜求める値＞
$$\rm{dp}[m][n]$$

　

最後に、diff コマンドなどにも用いられているレーベンシュタイン距離を求める DP を見てみましょう。

問題 10:　レーベンシュタイン距離 (diffコマンド)

2つの文字列 $S$, $T$ が与えられます。$S$ に以下の3種類の操作のいずれかを順次実施して $T$ に変換したいです。そのような一連の操作のうち、操作回数の最小値を求めよ。

(操作)
＜変更＞ Sの中から文字S[ i ]を1個選んで、その文字を好きな文字に変更します。
＜削除＞ Sの中から文字S[ i ]を1個選んで、その文字を削除します。
＜挿入＞ Sの好きな箇所に好きな文字を挿入します。

【制約】
・$1 \le |S|, |T| \le 1000$

【数値例】
1)
**　$S = $"abc"**
**　$T = $"addc"**
**　答え: 2 (abc -(変更)-> adc -(挿入)-> addc)**

2)
**　$S = $"pirikapirirara"**
**　$T = $"poporinapeperuto"**
**　答え: 10**

---

【解法】
$\rm{dp}[i+1][j+1]$ := $S$ の $i$ 文字目までを変換して、$T$ の $j$ 文字目までへと変換するための最小操作回数
とします。$\rm{dp}[i][j]$, $\rm{dp}[i+1][j]$, $\rm{dp}[i][j+1]$ を使って $\rm{dp}[i+1][j+1]$ を表すことを考えると次のようになります。

• 変更操作 ($S$ の $i$ 文字目を $T$ の $j$ 文字目に変更)
  　　　　　$S[i] = T[j] なら、\rm{dp}[i+1][j+1] = \rm{dp}[i][j]$
  　　　　　$S[i] \neq T[j] なら、\rm{dp}[i+1][j+1] = \rm{dp}[i][j] + 1$
  　

• 削除操作 ($S$ の $i$ 文字目を削除)
  $$\rm{dp}[i+1][j+1] = \rm{dp}[i][j+1] + 1$$

• 挿入操作 ($T$ の $j$ 文字目を削除)
  $$\rm{dp}[i+1][j+1] = \rm{dp}[i+1][j] + 1$$

まとめると、

＜DP漸化式＞

\rm{dp}[i+1][j+1] = \left\{
\begin{array}{ll}
\min(\rm{dp}[i][j], \rm{dp}[i][j+1] + 1, \rm{dp}[i+1][j] + 1) & (S[i] == T[j]) \\
\min(\rm{dp}[i][j] + 1, \rm{dp}[i][j+1] + 1, \rm{dp}[i+1][j] + 1) & (S[i] != T[j])
\end{array}
\right.

＜DP初期条件＞
$$\rm{dp}[0][0] = 0$$

＜求める値＞
$$\rm{dp}[|S|][|T|]$$

ソースコードにすると以下のようになります。添字 $(i, j)$ の回し方について、少し注意が必要です。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int INF = 1<<29;        // 十分大きい値にする

// 入力
int n, m;
string S, T;

// DP テーブル
int dp[1010][1010];

int main() {
  cin >> n >> m >> S >> T;

  // 初期化
  for (int i = 0; i < 1010; ++i) for (int j = 0; j < 1010; ++j) dp[i][j] = INF;
  dp[0][0] = 0;
    
  for (int i = -1; i < (int)S.size(); ++i) {
    for (int j = -1; j < (int)T.size(); ++j) {
      if (i == -1 && j == -1) continue;   // dp[0][0] は考慮済
      if (i >= 0 && j >= 0) {
        if (S[i] == T[j]) dp[i+1][j+1] = min(dp[i+1][j+1], dp[i][j]);
        else dp[i+1][j+1] = min(dp[i+1][j+1], dp[i][j] + 1);
      }
      if (i >= 0) dp[i+1][j+1] = min(dp[i+1][j+1], dp[i][j+1] + 1);
      if (j >= 0) dp[i+1][j+1] = min(dp[i+1][j+1], dp[i+1][j] + 1);
    }
  }

  cout << dp[S.size()][T.size()] << endl;
}

　
　

5 区間を分割する問題 --- 分かち書きなど

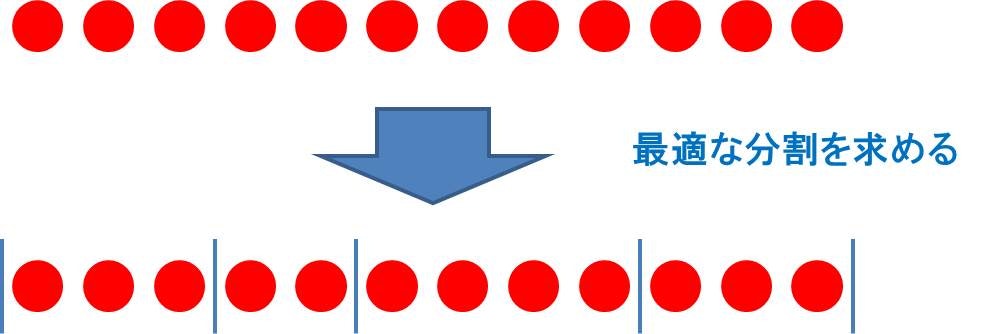
ナップサック DP は、$n$ 個の対象それぞれに対して「選ぶ」「選ばない」の2通りの選択肢を考えていく過程を効率よく実現できる手法でした。今回はこれを利用して、下図のような「連続する $n$ 個のアイテムを各区間に最適に分割する問題」を考えてみましょう。分かち書きや、発電計画問題などが、この枠組みに当てはまります。

さて、区間に分割することとナップサック DP との間にはどんな関係があるでしょうか。ナップサック DP では各アイテムに対して「選ぶ」「選ばない」を決めていましたが、今回の区間分割問題では、隣り合うアイテム間の隙間それぞれに対して「仕切りを入れる」「仕切りを入れない」を決めていきます。こうして、区間分割問題もナップサック DP のように考えることができます。

具体例として次のような発電計画問題を考えてみましょう。

問題 11:　発電計画問題

正の整数 $T$ が与えられ、$t = 0, ..., T-1$ のそれぞれについて時刻 $[t, t+1]$ の間に発電装置をオンにするかオフにするかを決める必要がある。発電計画においてオンになっている区間が $[l_0, r_0]$, $[l_1, r_1]$, ..., $[l_{k-1}, r_{k-1}]$ $(0 \le l_0 < r_0 < l_1 < r_1 < \dots < l_{k-1} < r_{k-1} \le T)$ であった場合の利得は、各 $i, j$ $(0 \le i < j \le T)$ に対して定義された値 $g[i][j]$ を用いて、$g[l_0][r_0] + g[l_1][r_1] + \dots + g[l_{k-1}][r_{k-1}]$ で与えられる。発電計画を最適化して得られる利得の最大値を求めよ。

【制約】
・$1 \le T \le 100$
・$0 \le g[i][j] \le 1000$

【数値例】
1)
**　$T = 4$**
**　$g = $**
**　　　$3, 7, 4, 8$**
**　　　$0, 5, 9, 7$**
**　　　$0, 0, 8, 5$**
**　　　$0, 0, 0, 6$**
**　答え: 13 (時刻 [0, 2] の利得 7 と、時刻 [3, 4] の利得 6 を足して 13 が最大です)**

---

【解法】
今回は緩和式ではなく漸化式の形で記述します。

$\rm{dp}[t]$ := 時刻 $[t-1, t]$ ではオフにしていた場合についての時刻 $t$ までの総利得の最大値
とします。

＜DP漸化式＞
$$\rm{dp}[t] = \max_{0 \le i < j < t} ( \rm{dp}[i] + g[i][j] )$$

＜DP初期条件＞
$$\rm{dp}[0] = 0$$

＜求める値＞
$$\rm{dp}[T+1]$$
(時刻は $T$ までですが、$\rm{dp}[T+1]$ まで更新してリターンすればちょうどいいです)

計算時間オーダーは、DPテーブルのサイズが $O(T)$ で、1個の DP 値を更新するのに平均で $O(T^2)$ だけの探索を必要とするので、合計で $O(T^3)$ になります。このような問題では多くの場合、発展的なデータ構造を用いることでオーダーを落とすことができますが、そのテクニックについて詳しく知りたい方はプログラミングコンテストチャレンジブックの「3-4 動的計画法を極める」のP.186以降がとても参考になると思います。

　

問題 12:　分かち書き

次に、分かち書きについて考えます。分かち書きとは、例えば

$$僕は君を愛している$$

といった文章を

$$僕　は　君　を　愛し　て　いる$$

といったように単語ごとに区切る作業です。英語に対しては必要ない作業ですが、日本語においては文章を系列データとして扱うための前処理として重要です。これも、「単語の出現しやすさ」と「単語と単語のつながりやすさ」を条件付確率場 (CRF) などによって学習した下では、DP で自然に実施することができます。単語 $w$ 自体の出現しにくさを表すコストを $c[w]$、単語 $v$, $w$ のつながりにくさを表すコストを $d[v][w]$ で表すことにします。また、入力文の文字数を $n$、$i$ 文字目から $j$ 文字目までの区間で得られる単語を $w(i, j)$ と表すことにします。

【解法】
$\rm{dp}[i][j]$ := $i$ 文字目の後ろで区切ったとき、最後の単語が $w(j, i)$ であった場合についての、それ以前の部分の分かち書きの最小コスト
とします。

＜DP漸化式＞
各 $0 \le j < i \le n$ に対して、
$$\rm{dp}[i][j] = \min_{0 \le k < j} (\rm{dp}[j][k] + c[w(j, i)] + d[w(k, j)][w(j, i)])$$

＜DP初期条件＞
$$\rm{dp}[0][0] = 0$$

＜求める値＞
$$\min_{0 \le j < n} \rm{dp}[n][j]$$

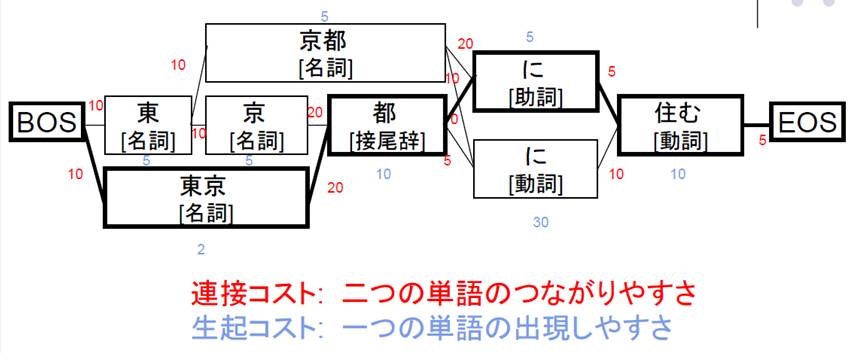
この DP のイメージは、以下の図 (日本語解析ツールMeCab, CaboCha の紹介より) がとてもわかりやすいです。この分かち書きに限らず、これまで見て来た DP はすべて有向非閉路グラフ (DAG) 上の最短経路問題 (と同じ構造の問題) とみなすことができます！

なお、分かち書き等を行う代表的なライブラリである Mecab の仕組みついては、以下の資料が参考になると思います:

• 日本語解析ツールMeCab, CaboCha の紹介
• T. Kudo et al., Applying Conditional Random Fields to Japanese Morphological Analysis, EMNLP 2004

おわりに

今回は系列順に漸化式を遷移させていくようなナップサック DP を特集しました。DP は数理計画や機械学習やパターン認識などで要素技術として様々な場面で使われています。そしてそれらは決して突飛なものではなく、とても自然なものに感じられたことと思います。次回はDPテーブルの持ち方や遷移様式が異なる DP の代表例として、区間 DP と bit DP を取り上げます！

次回以降の予定

区間 DP

・行列積問題

・最適二分探索木問題

・randomized quicksort における swap 回数の期待値 (SRM486 DIV1 Medium QuickSort)

・iwi問題 (TDPC I - イゥイ)

・回文の何か

・四則とか

・(余裕あったら) Monge性とか

bit DP

・巡回セールスマン問題

・完全マッチングの数え上げ問題

・トポロジカルソートの数え上げ問題 (ABC 041 D 徒競走)

・タイル色塗り (SRM532 DIV2 Hard DengklekPaintingSquares)

・数え上げお姉さん問題