Go to Qiita Advent Calendar 2024 Top
LoginSignup
438
405

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

明治大学総合数理Advent Calendar 2017

Day 17
@ZoneTsuyoshi

深層学習の最適化アルゴリズム

Last updated at Posted at 2017-12-17

追記情報

  • 2017.12.19：Chainer3.2.0 の Optimizer とのパラメータ対応，Optimizer の流儀について追記．
  • 2018.2.12：AdaMax, Nadam, Eve, GD by GD, AdaSecant について追記．

はじめに

深層学習の最適化手法に関してまとめを記します．

前提知識

  • 勾配降下法・ミニバッチ学習（オンライン学習）
  • 深層学習に関する基礎知識

紹介する最適化手法

  • 確率的勾配降下法（SGD）
  • MomentumSGD
  • ネステロフの加速法（NAG） (1983)
  • AdaGrad (2011)
  • RMSprop (2012)
  • AdaDelta (2012)
  • Adam (2014)
  • RMSpropGraves (2014)
  • SMORMS3 (2015)
  • AdaMax (2015)
  • Nadam (2016)
  • Eve (2016)
  • Santa （2016）
  • GD by GD (2016)
  • AdaSecant (2017)
  • AMSGrad (2018)
  • AdaBound, AMSBound (2019)

記号について

  • [1]は後の参考文献と対応している番号である．
  • ベクトルはbold体$\mathbf{a}$のように表す．
  • ベクトルの要素ごとの積は$\mathbf{a}\mathbf{b}$のように通常の積と表す．本来$\mathbf{a}\odot\mathbf{b}$と表すべきだが，書きやすさを選んだ．
  • ベクトルの要素ごとの商は$\mathbf{a}/\mathbf{b}$のように通常の商と同じように表す．本来$\mathbf{a}\oslash\mathbf{b}$と表すべきだが，書きやすさを選んだ．
  • スカラーとベクトルの間で演算を行っていた場合，スカラー$s$はすべての要素が1のベクトル$\mathbf{1}$との積$s\mathbf{1}$を指しているものとする．
  • 最適化するパラメータは$\mathbf{w}$で表す．
  • 最適化に用いる評価関数は$E(\mathbf{w})$で表す．平均二乗誤差や交差エントロピーを考えれば良い．
  • $t$はイテレーションを表す．ミニバッチ学習において，(1エポックにおけるバッチ数)$\times$(エポック数)$=$(イテレーション数)であり，何番目のイテレーションかを指す．
  • $\eta$は学習率（learning rate），$\mathbf{g}$は評価関数の勾配である．
  • また，本来，パラメータの更新において実行可能集合へ適切な射影を最後に行うべきであるが，省略して記載した．

確率的勾配降下法（SGD, Stochastic Gradient Descent）

数式として，次のように表せる．

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)})\\
\Delta\mathbf{w}^{(t)}=-\eta\mathbf{g}^{(t)}\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

ここで，$\eta$ は学習率（learning rate）を意味する．学習に時間がかかるということから近年あまり用いられて来なかったが，後述する学習率を adaptive に変える手法に比べ，学習率が一定であり，収束結果が安定していることから今でも用いられている．

Momentum SGD

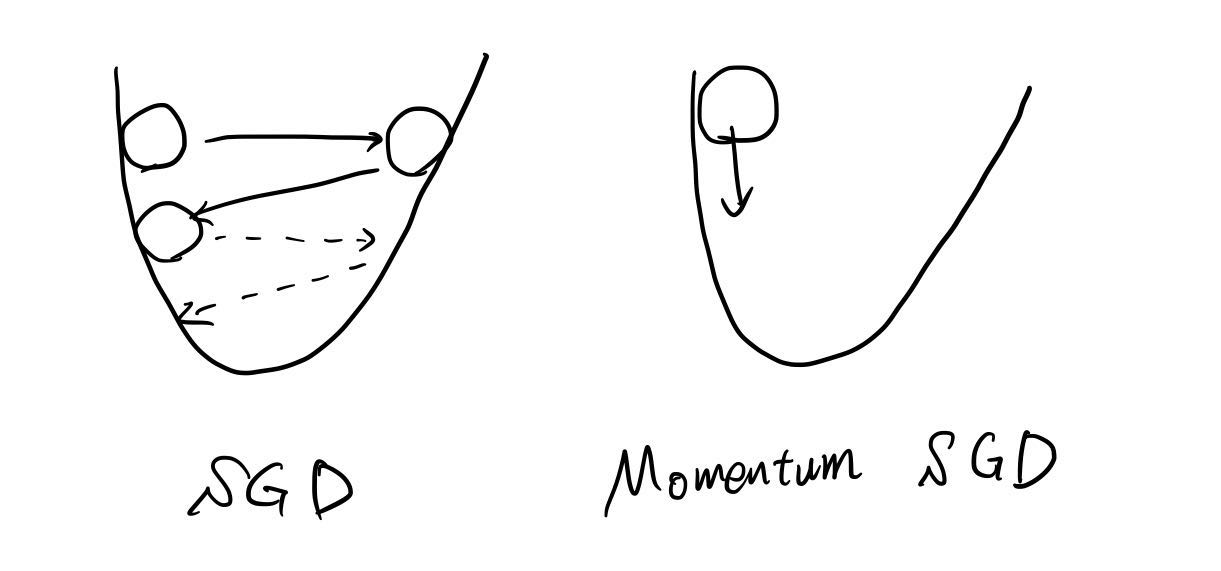
SGDは収束が遅く，また振動や鞍点に陥る問題が発生しやすい[1]．この問題を克服するため提案されたのが Momentum SGD である．Momentum SGD では，一期前の勾配情報$\Delta\mathbf{w}_{t-1}$を用いる．谷の間で振動する場合，一期前の勾配情報を用いることで振動を抑制できる（下図参照）．フラットな斜面の場合も収束するまでの時間を短くすることができる．また，安定した収束が得られることでも知られており，SGD とともに未だ健在な手法である．更新式は次のようになる．

image.png

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)})\\
\Delta\mathbf{w}^{(t)}=\mu\Delta\mathbf{w}^{(t-1)}-(1-\mu)\eta\mathbf{g}^{(t)}\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

ここで，$\mu$ は一期前の勾配情報を伝える比率を示すハイパーパラメータで，$\mu=0.9,\eta=0.01$で使われることが多い．

ネステロフの加速法（NAG） (1983)

ネステロフの加速法(Nesterov's Accelerated Gradient method)は，Momentum SGD の修正版であり，さらに収束への加速を増したものである．勾配の値を評価する位置を$\mathbf{w}^{(t)}+\mu\mathbf{w}^{(t-1)}$ とすることで，一期先の時刻を大雑把に見積もることができる[1,2]．更新式は以下のようになる．

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)}+\mu\mathbf{w}^{(t-1)})\\
\Delta\mathbf{w}^{(t)}=\mu\Delta\mathbf{w}^{(t-1)}-(1-\mu)\eta\mathbf{g}^{(t)}\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

$\mu=0.9,\eta=0.01$で与えられることが多い．

AdaGrad (2011)

MomentumSGD, NAG では振動抑制・収束加速に対する効果はあるが，収束方向に関する情報を用いていなかった．言い換えると，深層学習で考えるような多次元の問題では，勾配が急な方向には早く収束するが，勾配が緩やかな方向には収束に時間がかかることが起こり得る．

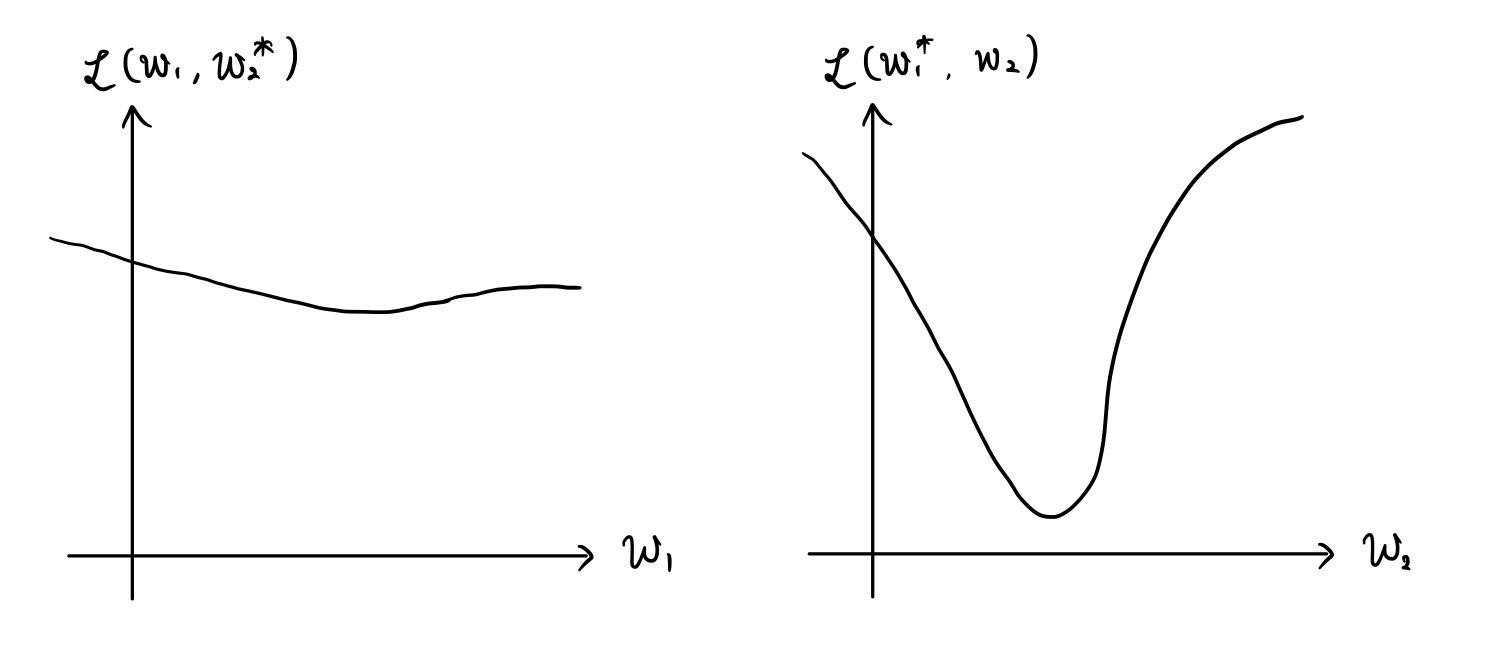
例えば，簡単のためパラメータ空間が２次元 $(w_1,w_2)$ であるとする．$w_1$ 軸に沿っては変化が緩やかで，$w_2$ 軸に沿って変化が急な場合，$w_2$ 軸に沿って収束したのちに時間をかけて $w_1$ 軸に沿って収束すると考えられる（下図参照）．２次元ではそれでも良いかもしれないが，高次元のパラメータ空間においては，スケールに合わせた勾配方向を定めた方が速く最適解に行き着くことが期待される．

image.png

この考えを取り入れ，各次元（各軸）ごとに学習率を調整していこうという手法の先駆けとなったのが AdaGrad（Adaptive subGradient descent） である[1,3]．更新式では次のように表せる．

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)})\\
\Delta\mathbf{w}^{(t)}=-\frac{\eta}{\sqrt{\sum_{s=1}^t(\mathbf{g}^{(s)})^2}}\mathbf{g}^{(t)}\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

第二式の$(\mathbf{g}^{(t)})^2$は要素ごとに二乗したベクトルを表しており，今までの更新量が大きい次元ほどルートの中身が大きくなり，更新されにくくなる．一方，今までの更新量が小さい次元ほどルートの中身が小さくなり，その方向に更新されやすくなる．

また，ハイパーパラメータ $\eta=0.001$ で与えられることが多い．

RMSprop （2012）

AdaGrad は次元に応じた学習率の変更を可能にしたが，最初に急な坂になっていて，その後も坂が続く場合に対応していなかった．すなわち，一度学習率が0に十分近くなってしまった次元に関しては，まだ坂があってもほとんど更新されなくなってしまうことである．

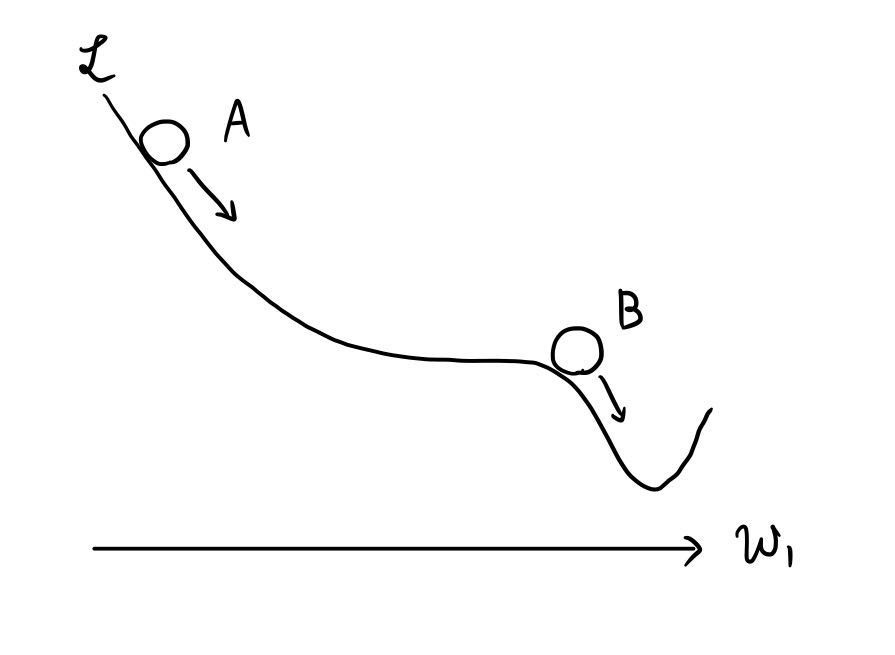
理解のために下図を見て欲しい．最初パラメータは地点Aにあったとしよう．地点Aでは勾配が急になっているので，このパラメータ $w_1$ の方向には更新量が大きくなる．そのため，AdaGrad の第二式における分母が大きくなる．ゆえに，地点Bに差し掛かったときに既に分母が大きくなってしまっているためにあまり更新がされなくなってしまう．

image.png

この改善策として提案されたのが RMSprop である[1]．RMSprop では，更新量の影響が$\rho^{t/2}$ に応じて指数的減衰していく．更新式としては次のようになる．

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)})\\
\mathbf{v}_t=\rho\mathbf{v}_{t-1}+(1-\rho)(\mathbf{g}^{(t)})^2\\
\Delta\mathbf{w}^{(t)}=-\frac{\eta}{\sqrt{\mathbf{v}_t+\varepsilon}}\mathbf{g}^{(t)}\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

第三式に注目すると，分母のルートの中身が $\mathbf{v}_t$ に変わっており，$\mathbf{v}_t$ は第二式の漸化式で表されている．$\mathbf{v}_t$ は，今までの勾配（更新量）を $\rho$ 倍して取り入れ，新しい勾配を $1-\rho$ 倍して取り入れている．すなわち，これまでの更新量に依存しつつも $\rho$ 倍して取り入れることで十分昔の勾配情報を無視することができる．それゆえ，先ほどの図において地点Bに差し掛かったときには，地点Aの勾配情報をほとんど無視して学習が進む．

また，$\varepsilon$ は分母が0になって発散してしまうのを防止するパラメータである．

ここで，$\mathbf{v}_0=\mathbf{0}$とし，ハイパーパラメータ$\varepsilon=10^{-6},10^{-8},\eta=0.01,\rho=0.99$で与えられることが多い．

AdaDelta (2012)

RMSprop では次元数のミスマッチの問題が解消されていなかった．実際，$\Delta\mathbf{w}$は次元量が長さ $N_w$ であるが，$\mathbf{g}$はその勾配を取っているので，次元量は $1/N_w$ となる（$N_w$ はパラメータの次元数）．

物理の感覚とのアナロジーで説明する．変位 $x$ の次元は L:length であるが，その時間微分である速度 $v$ の次元は $L/T$ (T:time)となる．すなわち，微分すると微分変数が持つ次元量が割られたことに相当する（微分を変化量の極限と考えれば自然なことである）．今回の場合，勾配 $\mathbf{g}$ は $\mathbf{w}$ で損失関数を微分した量なので，$1/N_w$ が次元量となる．AdaGrad や RMSprop の $\Delta\mathbf{w}$ に関する式を見ると，左辺の次元量が $N_w$，右辺の次元量が1となっていることが分かる．

すなわち，次元量が違うものを計算していたために，スケール変換に対応できていなかった[1,4]．これを解消したものが AdaDelta であり，ニュートン法を応用したものである．更新式は以下で与えられる．

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)})\\
\mathbf{v}_t=\rho\mathbf{v}_{t-1}+(1-\rho)(\mathbf{g}^{(t)})^2\\
\mathbf{u}_t=\rho\mathbf{u}_{t-1}+(1-\rho)(\Delta\mathbf{w}^{(t)})^2\\
\Delta\mathbf{w}^{(t)}=-\frac{\sqrt{\mathbf{u}_{t-1}+\varepsilon}}{\sqrt{\mathbf{v}_t+\varepsilon}}\mathbf{g}^{(t)}\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

$\Delta\mathbf{w}$ の式において，左辺も右辺も次元量が $N_w$ となり，一致していることが分かる．

ここで，$\mathbf{v}_0=\mathbf{u}_0=\mathbf{0}$ とし，ハイパーパラメータ$\rho=0.95$が多く使われている．

Adam (2014)

もっともよく使われている最適化アルゴリズムの一つである．Adam も RMSprop の改良版であり， 勾配に関しても以前の情報を指数的減衰させながら伝えることで，次元量の問題に対処している[5]．Adam の更新式は，以下で与えられる．

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)})\\
\mathbf{m}_t=\rho_1\mathbf{m}_{t-1}+(1-\rho_1)\mathbf{g}^{(t)}\\
\mathbf{v}_t=\rho_2\mathbf{v}_{t-1}+(1-\rho_2)(\mathbf{g}^{(t)})^2\\
\hat{\mathbf{m}}_t=\frac{\mathbf{m}_t}{1-\rho_1^t}\\
\hat{\mathbf{v}}_t=\frac{\mathbf{v}_t}{1-\rho_2^t}\\
\Delta\mathbf{w}^{(t)}=-\frac{\eta}{\sqrt{\hat{\mathbf{v}}_t+\varepsilon}}\hat{\mathbf{m}}_t\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

ここで，$\hat{\mathbf{m}}_t,\hat{\mathbf{v}}_t$は勾配，二乗勾配の不偏推定量となるように調整したものである．ハイパーパラメータは，$\eta=0.001,\rho_1=0.9,\rho_2=0.999,\varepsilon=10^{-8}$で与えられることが多い．

RMSpropGraves (2014)

Graves が提案した RMSprop の改良版アルゴリズムである[6]．主に手書き文字認識の分野で用いられている（例えば[7]や[8]）．更新式は以下のように与えられる．

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)})\\
\mathbf{m}_t=\rho\mathbf{m}_{t-1}+(1-\rho)\mathbf{g}^{(t)}\\
\mathbf{v}_t=\rho\mathbf{v}_{t-1}+(1-\rho)(\mathbf{g}^{(t)})^2\\
\Delta\mathbf{w}^{(t)}=-\frac{\eta}{\sqrt{\mathbf{v}_t-\mathbf{m}_t^2+\varepsilon}}\mathbf{g}^{(t)}\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

ハイパーパラメータは，$\eta=0.0001,\rho=0.95,\varepsilon=10^{-4}$で与えられることが多い．

SMORMS3 (2015)

SMORMS3 は RMSprop の問題点を曲率と LeCun 法によって克服したものである[9]．SMORMS3 の更新式は，以下で与えられる．

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)})\\
\mathbf{s}_{t}=1+(1-\boldsymbol{\zeta}_{t-1}\mathbf{s}_{t-1})\\
\boldsymbol{\rho}_t=\frac{1}{\mathbf{s}_t+1}\\
\mathbf{m}_t=\boldsymbol{\rho}_t\mathbf{m}_{t-1}+(1-\boldsymbol{\rho}_t)(\mathbf{g}^{(t)})\\
\mathbf{v}_t=\boldsymbol{\rho}_t\mathbf{v}_{t-1}+(1-\boldsymbol{\rho}_t)(\mathbf{g}^{(t)})^2\\
\boldsymbol{\zeta}_t=\frac{\mathbf{m}_t^2}{\mathbf{v}_t+\varepsilon}\\
\Delta\mathbf{w}^{(t)}=-\frac{\min\{\eta,\boldsymbol{\zeta}_t\}}{\sqrt{\mathbf{v}_t+\varepsilon}}\mathbf{g}^{(t)}\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

新しい勾配と以前の勾配を取り入れる比率を表すパラメータ $\rho$ を適応的に変化させていることがポイントである．

AdaMax (2015)

Adam を無限次元ノルムに対応させたものが AdaMax である[8]．更新式は以下で与えられている．

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)})\\
\mathbf{m}_t=\rho_1\mathbf{m}_{t-1}+(1-\rho_1)\mathbf{g}^{(t)}\\
\mathbf{v}_t=\max\{\rho_2\mathbf{v}_{t-1},|\mathbf{g}^{(t)}|\}\\
\Delta\mathbf{w}^{(t)}=-\frac{\alpha}{1-\rho_1^t}\frac{\mathbf{m}_t}{\mathbf{v}_t}\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

Nadam (2016)

ネステロフの加速法を Adam に取り入れたものが Nadam である[11]．Nadam のアルゴリズムは以下で与えられている．

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)})\\
\mathbf{m}_t=\mu_t\mathbf{m}_{t-1}+(1-\mu_t)\mathbf{g}^{(t)}\\
\mathbf{v}_t=\rho\mathbf{v}_{t-1}+(1-\rho)(\mathbf{g}^{(t)})^2\\
\hat{\mathbf{m}}_t=\frac{\mu_{t+1}}{1-\prod_{i=1}^{t+1}\mu_i}\mathbf{m}_t+\frac{1-\mu_t}{1-\prod_{i=1}^t\mu_i}\mathbf{g}_t\\
\hat{\mathbf{v}}_t=\frac{\rho}{1-\rho^t}\mathbf{v}_t\\
\Delta\mathbf{w}^{(t)}=-\frac{\alpha_t}{\sqrt{\hat{\mathbf{v}}_t+\varepsilon}}\hat{\mathbf{m}}_t\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

ここで，${\mu_t},{\alpha_t}$ はステップ数に依存したパラメータとなっているが，ほとんどの場合固定して与えられる．

Eve (2016)

Eve は，相対的変化が大きければ学習率を削減し，小さければ上昇させることでフラットエリアで学習を高速化できるよう Adam を改良したものである[13]．更新式は以下で与えられる．

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)})\\
\mathbf{m}_t=\rho_1\mathbf{m}_{t-1}+(1-\rho_1)\mathbf{g}^{(t)}\\
\mathbf{v}_t=\rho_2\mathbf{v}_{t-1}+(1-\rho_2)(\mathbf{g}^{(t)})^2\\
\hat{\mathbf{m}}_t=\frac{\mathbf{m}_t}{1-\rho_1^t}\\
\hat{\mathbf{v}}_t=\frac{\mathbf{v}_t}{1-\rho_2^t}\\
\delta_t=\left\{\begin{array}{ll}k+1&(E(\mathbf{w}^{(t-1)})\ge\hat E_{t-2})\\1/(K+1)&(E(\mathbf{w}^{(t-1)})<\hat E_{t-2})\end{array}\right.,
\Delta_t=\left\{\begin{array}{ll}K+1&(E(\mathbf{w}^{(t-1)})\ge\hat E_{t-2})\\1/(k+1)&(E(\mathbf{w}^{(t-1)})<\hat E_{t-2})\end{array}\right.\\
c_t=\min\left\{\max\left\{\delta_t,\frac{E(\mathbf{w}^{(t-1)})}{\hat E_{t-2}}\right\},\Delta_t\right\}\\
\hat E_{t-1}=c_t\hat E_{t-2}\\
r_t=\frac{|\hat E_{t-1}-\hat E_{t-2}|}{\min\{\hat E_{t-1},\hat E_{t-2}\}}\\
d_t=\rho_3d_{t-1}+(1-\rho_3)r_t\\
\Delta\mathbf{w}^{(t)}=-\frac{\eta}{d_t\sqrt{\hat{\mathbf{v}}_t+\varepsilon}}\hat{\mathbf{m}}_t\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

Santa (2016)

Santa（Stochastic AnNealing Thermostats with Adaptive Momentum）は，Adam や RMSprop に MCMC（マルコフ連鎖モンテカルロ）法を取り入れたものである．論文[14]では，Euler 型の Santa-E と SSS (対称分割法，Symmetric Separation Scheme)型の Santa-SSS について述べられている．その中でも，Santa-SSS が Adam より高い精度を示している．

Santa-E

Santa-E アルゴリズムは以下で与えられている．
Santa-E.png

ここで，今まで勾配を$\mathbf{g}_t$としていたが，$\tilde{\mathbf{f}}_t$で表されていることに注意されたい．Santa には exploration （探索）ステップと refinement （精錬）ステップがある．探索ステップはガウスノイズ$\boldsymbol{\zeta}$を載せながら最適解の近くまで探索するステップであり，精錬ステップはその後の学習をするステップである．MCMC というと計算量が肥大するのではないかと思った方もいるかもしれないが，見てわかる通り，従来まとめていたステップを分けただけであり，イテレーションあたりの計算量も必要メモリも微増である．

Santa-SSS

Santa-SSS アリゴリズムは以下で与えられている．
Santa-SSS.png

ここで，$\mathbf{g}_t$はフィッシャー情報量を表しており，Santa-SSS は mSGNHT を拡張したものになっている．また，このアルゴリズムの収束性は，リーマン情報幾何を学んでいる人は，論文[14]を読むと理解できると思う．

論文での結果は次の通りであった．
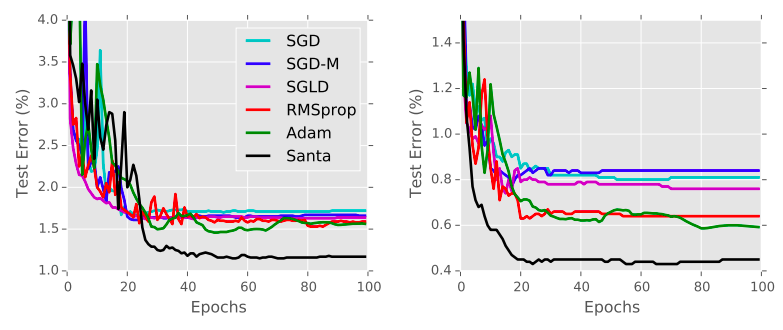
Santa-Result.png

見ての通り，Santa(Santa-SSS) が bunrin 期間を過ぎると，Adam 等の他のオプティマイザを寄せ付けない圧倒的な性能の良さを示していることがわかる．これは，Santa ではノイズを付加して探索することでパラメータ空間を限りなく探索して大域的な谷を見つけているからである．そのため，大域的極小解に近い極小解を得ているだけの他のアルゴリズムの追随を許していないのである．

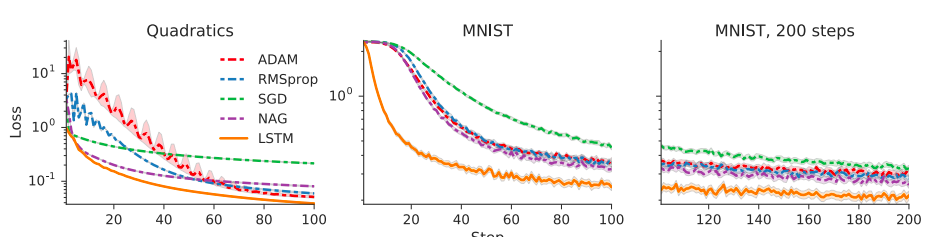
GD by GD (2016)

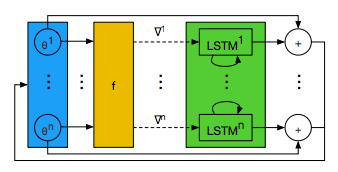
GD by GD(Gradient Descent by Gradient Descent)は，最適化アルゴリズムも学習問題と捉え，学習して最適化構造を決めて行くものである[16]．イメージ図は次のとおりである．

GDbyGD.png

最適化される Optimizee だけでなく，最適化する Optimizer もロス情報で最適化していこうという発想である．具体的には，LSTM optimizer を提案している．

optimizer_LSTM.png

また，この LSTM optimizer では loss が Adam 等より減りが早いという結果を得ている．

LSTM_loss.png

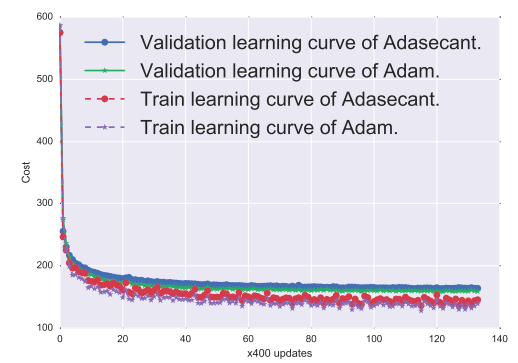
AdaSecant (2017)

AdaSecant はロスの曲率情報（２階微分）まで伝えて最適化しようというアイディアである[17]．これまでにもヘシアンを活用しようというアイディアはあったが，逆行列の計算に時間的コストがかかる上，対角ヘシアンの逆行列はヘシアンの逆行列の対角化の近似として不適切であることも示されていた．

　AdaSecant では，Newton 法と準 Newton 法（quasi-Newton）がパラメータ空間でアフィン不変であることに目をつけた．また，確率的 rank-1 quasi-Newton 法となっており，アフィン変換に対するロバスト性が確保できている．アルゴリズム的には，勾配の secant 近似がヘシアンの対角成分の近似となっていることを活用している．アルゴリズムは次のとおりである．

AdaSecant_algorithm.png

loss が Adam 等より減衰していることも示されている．

AdaSecant_loss.png

AMSGrad (2018)

Adam, RMSProp, AdaDelta, NAdam では，指数移動平均による指数減衰が使われていた．しかし，特定の標本による勾配情報が重要なとき，そのミニバッチにおける勾配情報は指数減衰によって，直ぐに消えてしまい，最適解に収束できない問題が報告されている．そこで，重要な勾配情報が直ぐに消えてしまわないように Adam を改良した手法が AMSGrad である[18]．具体的な更新式は，以下で与えられる．

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)})\\
\mathbf{m}_t=\rho_1\mathbf{m}_{t-1}+(1-\rho_1)\mathbf{g}^{(t)}\\
\mathbf{v}_t=\rho_2\mathbf{v}_{t-1}+(1-\rho_2)(\mathbf{g}^{(t)})^2\\
\hat{\mathbf{v}}_t=\max\{\hat{\mathbf{v}}_{t-1},\mathbf{v}_t\}\\
\Delta\mathbf{w}^{(t)}=-\frac{\eta}{\sqrt{\hat{\mathbf{v}}_t+\varepsilon}}{\mathbf{m}}_t\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

キーとなるのは，４行目の $\hat{\mathbf{v}}_t$ の更新式である．1時点前の勾配二乗と現在の指数減衰勾配
二乗を比較して，各次元毎に大きい方を採用している．すなわち，学習に重要なミニバッチの勾配情報を長期間に渡って残すことができる．これによって，不必要な情報の（適応的な）学習率が大きくなる問題を防ぐことができる．

AdaBound, AMSBound (2019)

AMSGrad は，既存手法である Adam, RMSProp, AdaDelta に対して，著しい成功を収められなかった．その原因の一つは，（適応的な）学習率が不必要に大きくなる問題を抑えることには成功したが，学習率が不必要に小さくなる問題を解決できていなかったからである．

Adam では，適応的な学習率により，学習を速く進めることができるが，学習が進んだ後でも学習率の乱高下により，汎化誤差を上手く抑えることができない問題点があった．一方，固定学習率を採用している SGD では，最終的な汎化誤差は小さくできるが，そこまで進むのに時間がかかり過ぎるという問題点があった．そこで，序盤は Adam，終盤は SGD のように振る舞う最適化手法として登場したのが AdaBound, AMSBound である[19]．

前者（AdaBound）は Adam を改良した手法，後者（AMSBound）は AMSGrad を改良した手法であるが，前者の式だけを示す．

\mathbf{g}^{(t)}=\nabla E(\mathbf{w}^{(t)})\\
\mathbf{m}_t=\rho_1\mathbf{m}_{t-1}+(1-\rho_1)\mathbf{g}^{(t)}\\
\mathbf{v}_t=\rho_2\mathbf{v}_{t-1}+(1-\rho_2)(\mathbf{g}^{(t)})^2\\
\hat{\boldsymbol{\eta}}_t=\frac{1}{\sqrt t}\mathrm{Clip}\left(\frac{\eta}{\sqrt{\mathbf{v}_t}},\eta_l(t),\eta_h(t)\right)\\
\Delta\mathbf{w}^{(t)}=-\hat{\boldsymbol{\eta}}_t\ {\mathbf{m}}_t\\
\mathbf{w}^{(t+1)}=\mathbf{w}^{(t)}+\Delta\mathbf{w}^{(t)}

ここで鍵となるのが，４行目の適応的学習率であり，
適応的学習率の下限と上限をそれぞれ関数 $\eta_l(t),\ \eta_u(t)$ で定めている．
SGDの場合，$\eta_l\equiv\eta_u\equiv\alpha$ (const.)であり，Adam の場合，
$\eta_l\equiv0,\eta_u\equiv\infty$ である．これらの関数によって定める区間 $[\eta_l(t),\eta_u(t)]$ を $[0,\infty)$ から $[\alpha,\alpha]$ に徐々に狭めていくことで序盤は Adam，終盤は SGD のような振る舞いを達成しようというのがここでのアイディアである．

最後に

  • 深層学習は日進月歩の分野であり，新しい手法が次から次へと出てくる．

参考文献

  1. 瀧雅人，機械学習スタートアップシリーズ これならわかる深層学習入門，講談社，2017．
  2. Yurri Nesterov. A method of solving a convex programming problem with convergence rate O(1/sqr(k)), http://www.cis.pku.edu.cn/faculty/vision/zlin/1983-A%20Method%20of%20Solving%20a%20Convex%20Programming%20Problem%20with%20Convergence%20Rate%20O(k%5E(-2))_Nesterov.pdf, 1983．
  3. John Duchi, Elad Hazen, Yoram Singer. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization, http://www.jmlr.org/papers/volume12/duchi11a/duchi11a.pdf, 2011.
  4. Matthew D. Zeiler. ADADELTA: AN ADAPTIVE LEARNING RATE METHOD, https://arxiv.org/pdf/1212.5701.pdf, 2012.
  5. Diederik P. Kingma, Jimmy Lei Ba. ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION, https://arxiv.org/pdf/1412.6980.pdf, 2015.
  6. Alex Graves, Generating Sequences With Recurrent Neural Network, https://arxiv.org/pdf/1308.0850.pdf, 2014.
  7. Karol Gregor, Ivo Danihelka, Andriy Mnih, Charles Blundell, Daan Wierstra. Deep AutoRegressive Networks, https://arxiv.org/pdf/1310.8499.pdf, 2014.
  8. Ganbin Zhou, Ping Luo, Rongyu Cao, Fen Lin, Bo Chen, Qing He. Mechanism-Aware Neural Machine for Dialogue Response Generation. aaai. 2017.
  9. Simon Funk. RMSprop loses to SMORMS3 - Beware the Epsilon!. http://sifter.org/~simon/journal/20150420.html, 2015.
  10. AdaGrad, RMSProp, AdaDelta, Adam, SMORMS3，https://qiita.com/skitaoka/items/e6afbe238cd69c899b2a．
  11. Timothy Dozat. INCORPORATING NESTEROV MOMENTUM INTO ADAM. https://openreview.net/pdf?id=OM0jvwB8jIp57ZJjtNEZ, 2016.
  12. OPTIMIZER 入門 ~線形回帰からAdamからEveまで，https://qiita.com/deaikei/items/29d4550fa5066184329a
  13. Jayanth Koushik & Hiroaki Hayashi. IMPROVING STOCHASTIC GRADIENT DESCENT WITH FEEDBACK, https://arxiv.org/pdf/1611.01505.pdf, 2016.
  14. Changyou Chen, David Carlson, Zhe Gan, Chunyuan Li, Lawrence Carin Bridging the Gap between Stochastic Gradient MCMC and Stochastic Optimization，http://proceedings.mlr.press/v51/chen16c.pdf, 2016.
  15. Chunyuan Li, Changyou Chen, Kai Fan and Lawrence Carin. High-Order Stochastic Gradient Thermostats for Bayesian Learning of Deep Models, https://www.cse.buffalo.edu/~changyou/PDF/msgnht_poster.pdf, n.d.
  16. Marcin Andrychowicz, Misha Denil, Sergio Gomez Colmenarejo, Matthew W. Hoffman, David Pfau, Tom Schaul, Brendan Shillingford, Nando de Freitas. Learning to learn by gradient descent by gradient descent. http://papers.nips.cc/paper/6461-learning-to-learn-by-gradient-descent-by-gradient-descent.pdf, 2016.
  17. Caglar Gulcehre, Jose Sotelo, Marcin Moczulski, Yoshua Brengio. A Robust Adaptive Stochastic Gradient Method for Deep Learning. https://arxiv.org/pdf/1703.00788.pdf, 2017.
  18. Sashank J. Reddi, Satyen Kale & Sanjiv Kumar. On the Convergence of Adam and Beyond. http://www.satyenkale.com/papers/amsgrad.pdf, 2018.
  19. Liangchen Luo, Yuanhao Xiong, Yan Liu, Xu Sun. Adaptive Gradient Methods with Dynamic Bound of Learning Rate. https://openreview.net/forum?id=Bkg3g2R9FX, 2019.
438
405
5

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
438
405

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?