はじめに
千葉大学/Nospareの米倉です.今回はカルマンフィルターについて解説していきたいと思います.
カルマンフィルターで何が出来るの?
フィルターとあるように,カルマンフィルターが出来る基本的なことは線形ガウス状態空間モデルのフィルタリング密度を逐次的に求めることです.ここで2つのキーワード,「線形ガウス状態空間モデル」と「フィルタリング密度」という単語が出てきましたので,まずはそれらについて解説します.
線形ガウス状態空間モデルとは
状態空間モデルとは2つの確率過程からなります.1つは潜在変数・状態変数・隠れ変数といわれるもので,これは直接観測できないがマルコフ連鎖に従う変数だとモデリングされます.例えば景気の良し・悪し等,概念として存在するけれど直接は観測できないものを想像してください.2つめは観測値で,これは直接観測できるもの,つまりデータです.ただし変数に依存して観測されるとします.今の例ですと,例えば株価などを想像してください.意味としては株価は景気の良し悪しに依存して決まるということです.この観測値にも「状態変数で条件づけると過去の自分自身とは独立となる」という仮定を置きます.
次に小林先生の過去の記事と被りますが,数式を用いて状態空間モデルを定義したいと思います.まず$t$期の状態変数を$x_{t}$とかき,観測値を$y_t$とかきます.次に状態変数が従うマルコフ連鎖の密度関数を$f(x_{t}\mid x_{t-1})$,$y_{t}$を$x_{t}$で条件づけた時の密度関数を$g(y_{t}\mid x_{t})$と一般的な形として書くことができ,この2つの密度関数で状態空間モデルはモデリングされます.以下は小林先生の記事からの画像の転用で,状態空間モデルの変数の依存関係が目で分かると思います.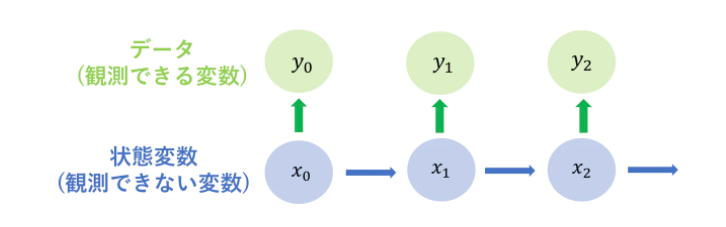
$x_{1:t}:=(x_1,...,x_t)$,$y_{1:t}:=(y_1,...,y_t)$とします.この時マルコフ性とは$x_{1:t-1}$で条件づけた$x_t$の条件付き密度$p(x_t\mid x_{1:t-1})$が$f(x_t\mid x_{t-1})$となることを指します.一方で,観測値の条件付き独立の仮定とは$p(y_t\mid y_{1:t-1},x_t)=g(y_t\mid x_t)$となること指します.
線形ガウス状態空間モデルとは$f(x_{t}\mid x_{t-1})$と$g(y_{t}\mid x_{t})$を線形かつガウシアンとモデリングした状態空間モデルのことです.${x_t}$を$d_x$次元のベクトル,${y_t}$を$d_y$次元のベクトルとしたときにこれを具体的に書くと,$$x_{t}=Ax_{t-1}+u_{t}$$ $$y_{t}=Bx_{t}+v_{t}$$
となります.ここで,$A$は$d_x\times d_x$行列,$B$は$d_y\times d_x$行列,$u_t$と$v_t$はそれぞれ多変量正規分布$N(0,\Sigma)$,$N(0,R)$に独立に従う確率ベクトルだとします.つまりこのモデリングだと,$f(x_t\mid x_{t-1})=N(x_t;Ax_{t-1},\Sigma), g(y_t\mid x_t)=N(y_t;Cx_t,R)$となります.ここで$N(a;b,c)$は$a$で評価した平均ベクトル$b$,共分散行列$c$の多変量正規分布の密度関数です.ここでは簡単化のために両者を独立としたり,$A,B,\Sigma,R$が時間$t$に依存しないようにしていますが拡張も可能です.下のコードは$d_x=d_y=2$の時の,線形ガウス状態空間モデルから擬似データを生成するJuliaのコードです.
function Lgauss2(A,B,Σ,R,T,x0)
# x' = Ax + N(0,Σ) A :dx×dx
# y' = Bx'+ N(0,R) B :dy⨱dx
x = zeros(2,T+1)
y = zeros(2,T)
x[:,1] = x0
for i in 1:T
x[:,i+1] = A*x[:,i] + rand(MvNormal(Σ))
y[:,i] = B*x[:,i+1] + rand(MvNormal(R))
end
return(x[:,2:T+1],y)
end
状態空間モデルのフィルタリング
状態空間モデルにおけるフィルタリングとは$y_{1:t}$を所与とした時の状態変数$x_t$の条件付き密度関数,$p(x_{t}\mid y_{1:t})$を求めることを指します.状態空間モデルの一般形を用いると,ベイズの定理と条件付き独立の仮定から,$$p(x_{t}\mid y_{1:t})=\frac{p(y_{t}\mid y_{1:t-1},x_t)p(x_t\mid y_{1:t-1})}{\int p(y_{t}\mid y_{1:t-1},x_t)p(x_t\mid y_{1:t-1})dx_{t}}$$ $$= \frac{g(y_{t}\mid x_t)p(x_t\mid y_{1:t-1})}{\int g(y_{t}\mid x_t)p(x_t\mid y_{1:t-1})dx_{t}}$$と計算できます.ここで$p(x_t\mid y_{1:t-1})$は「予測密度」とよばれ,$$p(x_t\mid y_{1:t-1})=\int p(x_t,x_{t-1}\mid y_{1:t-1})dx_{t-1}=\int f(x_t\mid x_{t-1}) p(x_{t-1}\mid y_{1:t-1})dx_{t-1}$$とマルコフ性から計算できます.このように$t$期のフィルタリング密度の計算には$t$期の予測密度が現れ,$t$期の予測密度の計算には$t-1$期のフィルタリング密度が現れるので,フィルタリング密度の計算→予測密度の計算→フィルタリング密度の計算・・・と逐次的に計算を行うことになります.
一般的に,状態空間モデルのフィルタリング密度の計算や予測密度の計算は,上で確認した通り複雑な積分を伴うために解析的に行うことが出来ません.しかし線形ガウス状態空間モデルならばカルマンフィルターを用いてそれらが可能になります.ここでいう解析的とは,例えばモンテカルロ計算等の数値近似がいらないという意味です.
多変量正規分布の計算
ここではカルマンフィルターの導出に必要な,多変量正規分布のある計算結果を証明抜きで述べます.今多変量正規分布に従う2つの確率変数ベクトル$X$と$Y$があり,$X\sim N(m_0,Q_0),Y\mid X\sim N(BX,R)$とします.このとき,$X\mid Y=y$は$N(m_1,Q_1)$に従います.ここで,$$Q_1=Q_0[I_{d_x}-B^\top (BQ_0B^\top+R)^{-1}BQ_0)]$$ $$m_1=[I_{d_x}-Q_0B^\top(BQ_0B^\top+R)^{-1}B]m_0+Q_0B^\top(BQ_0B^\top+R)^{-1}y$$
です.
カルマンフィルター
今までの結果から,カルマンフィルターを帰納法的に導出します.$t-1$期においてフィルタリング密度$p(x_{t-1}\mid y_{1:t-1})$は$N(m_{t-1},Q_{t-1})$に従っているとしましょう.$x_{t}=Ax_{t-1}+u_{t}$より普通のガウス分布の積分が出来て,$$p(x_t\mid y_{1:t-1})=N(Am_{t-1},AQ_{t-1}A^\top+\Sigma)$$と予測分布が求まります.$E_t:=AQ_{t-1}A^\top+\Sigma$とし,先ほど多変量正規分布の計算の結果を用いると,$$p(x_t\mid y_{1:t})=N(m_t,Q_t)$$ $$Q_t=E_t[I_{d_x}-B^\top (BE_tB^\top+R)^{-1}BE_t)]$$ $$m_t=[I_{d_x}-E_tB^\top(BE_tB^\top+R)^{-1}B]Am_{t-1}+E_tB^\top(BE_tB^\top+R)^{-1}y_t$$ともとまります.まとめると,
- $t$期の予測密度$p(x_t\mid y_{1:t-1})=N(Am_{t-1},AQ_{t-1}A^\top+\Sigma)$が計算されている.
- データ$y_t$を観測する.
- $Q_t,m_t,E_t$を計算してフィルタリング密度$p(x_t\mid y_{1:t})=N(m_t,Q_t)$を求める.
- $t+1$期の予測密度$p(x_{t+1}\mid y_{1:t})=N(Am_{t},AQ_{t}A^\top+\Sigma)$を求める.
というプロセスを繰り返し行うことになります.以上の様な,線形ガウス状態空間モデルのフィルタリング密度と予測密度を逐次的に求めるアルゴリズムをカルマンフィルターと呼びます.
参考までにJuliaでの実装例を載せます.KFfilter2は$d_x=d_y=2$の時の予測密度とフィルタリング密度の平均,分散を各$t$で計算する関数です.
function KFfilter2(A,B,Σ,R,data,Q0,m0)
# x' = Ax + N(0,Σ) A :dx×dx
# y' = Bx'+ N(0,R) B :dy⨱dx
n = length(data[1,:])
Qc = Q0
mc = m0
fm = []
fQ = []
pm = []
pQ = []
for i in 1:n
y = data[:,i]
predmean = A*mc
predvar = A*Qc*A'+Σ
push!(pm,predmean)
push!(pQ,predvar)
E = A*Qc*A' + Σ
Qn = E*(I+zeros(2,2) - B'*inv(B*E*B' + R)*B*E)
mn = (I+zeros(2,2) - E*B'inv(B*E*B'+R)*B)*A*mc + E*B'*inv(B*E*B'+R)*y
push!(fm,mn)
push!(fQ,Qn)
Qc = copy(Qn)
mc = copy(mn)
end
return(fm,fQ,pm,pQ)
end
カルマンフィルターの数値例
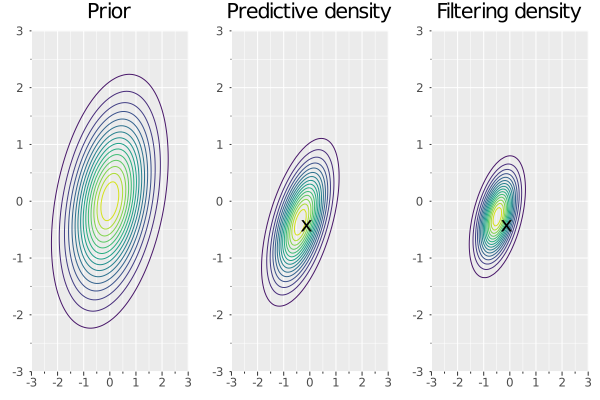
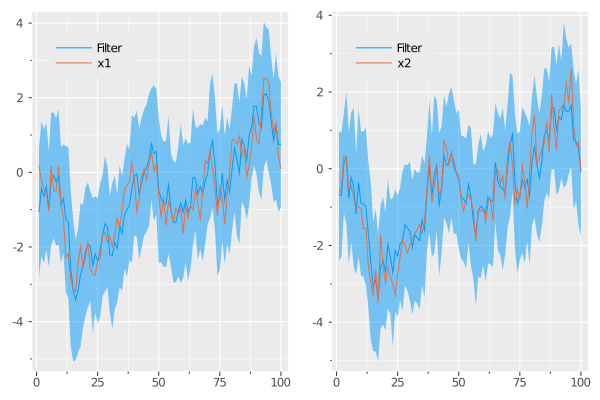
最後にJuliaを用いた実装例を見ます.モデルのパラメータや事前分布等はコードにあるように設定し,サンプルサイズ100の線形ガウス状態空間モデルから擬似データを生成して,それにカルマンフィルターを適用しました.上の図は事前分布,$t=99$期の予測密度,$t=100$期のフィルタリング密度の等高線で,図の中の$x$は$t=100$期の状態変数の値を指します.下の図は推定したフィルタリング密度を用いた状態変数の予測とその95%信頼区間(青色)と,シミュレートした状態変数(オレンジ)をプロットしたものです.
using Distributions
using LinearAlgebra
using Plots
using StatsPlots
using StatsBase
theme(:ggplot2)
# set paramaters of the model
A = [0.5 0.4;0.6 0.3]
B = I + zeros(2, 2)
P = [0.9 0.3;0.3 0.9]
Σ = 0.3.*P
R = 0.5.*P
T = 100
x0 = rand(MvNormal(P))
# simulate from LGmodel
x,y = Lgauss2(A,B,Σ,R,T,x0)
# run KF
Q0 = P
m0 = x0
fm,fQ,pm,pQ = KFfilter2(A,B,Σ,R,y,Q0,m0)
# calculate prior, filtering density and predictive density at time t,t-1
x_grid = range(-3.0, 3.0, length = 100)
y_grid = range(-3.0, 3.0, length = 100)
priordist = MvNormal(P)
filterdist = MvNormal(fm[100],fQ[100])
predictiondist = MvNormal(pm[99],pQ[99])
z1 = [pdf(priordist, [i,j]) for i in y_grid, j in x_grid]
z2 = [pdf(predictiondist, [i,j]) for i in y_grid, j in x_grid]
z3 = [pdf(filterdist, [i,j]) for i in y_grid, j in x_grid]
a=contour(x_grid,y_grid, z1,fill = false,color = :viridis, cbar = false,title="Prior")
contour(x_grid,y_grid, z2,fill = false,color = :viridis, cbar = false,title="Predictive density")
b=annotate!(x[1,100], x[2,100], "x", color = :black)
contour(x_grid,y_grid, z3,fill = false,color = :viridis, cbar = false,title="Filtering density")
c=annotate!(x[1,100], x[2,100], "x", color = :black)
plot(a,b,c,layout=(1,3))
# savefig("kalman.png")
# estimation
est_state1 = zeros(100,100)
est_state2 = zeros(100,100)
CIest1 = zeros(100)
CIest2 = zeros(100)
for i in 1:100
est = rand(MvNormal(fm[i],Symmetric(fQ[i])),100)
est_state1[i,:] = est[1,:]
est_state2[i,:] = est[2,:]
CIest1[i] = percentile(est_state1[i,:],97.5) - percentile(est_state1[i,:],2.5)
CIest2[i] = percentile(est_state2[i,:],97.5) - percentile(est_state2[i,:],2.5)
end
est1 = mean(est_state1, dims=2)
est2 = mean(est_state2, dims=2)
plot(est1,ribbon=CIest1,fillalpha=.5,label="Filter",foreground_color_legend = nothing,legend=:topleft)
a=plot!(x[1,:],label="x1")
plot(est2,ribbon=CIest2,fillalpha=.5,label="Filter",foreground_color_legend = nothing,legend=:topleft)
b=plot!(x[2,:],label="x2")
plot(a,b,layout=(1,2))
# savefig("kalman2.png")
おわりに
株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospare までお問い合わせください.