[Python]particlesパッケージで逐次モンテカルロ法を適用してみた（前編）

こんにちは，株式会社Nospareリサーチャー・千葉大学の小林です．本記事ではAn Introduction to sequential Monte Carloという逐次モンテカルロ法（sequential Monte Carlo, SMC）に関する本

に付随しているparticlesというPythonモジュールを紹介したいと思います．SMCはたくさんの変数（パーティクル）を発生させ，それらのリサンプリング，値の更新，重み付けを繰り返すことで逐次的にフィルタリング密度の近似などを行うモンテカルロ法の一種で，状態空間モデルなどに対して広く適用することができます．線形ガウス状態空間モデルの場合にはカルマンフィルターが適用できますが，非ガウス非線形モデルの場合にはシミュレーションに基づくSMCが有用となります．

状態空間モデル

まず状態空間モデルについて簡単に説明します．状態空間モデルは観測されるデータ$Y_t, (t=0,\dots,T)$と観測されない状態変数$X_t, (t=0,\dots,T)$からなる時系列モデルです．$X_t$はマルコフ過程に従い，$Y_t$は$X_t$を所与として条件付き独立です．状態変数の初期分布の密度関数を$p_0^\theta(x_0)$，$X_t$の条件付き密度を$p_t^\theta(x_t|x_{t-1})$，$Y_t$の条件付き密度を$f_t^\theta(y_t|x_t)$とすると，同時密度は

p^\theta_T(y_{0:T},x_{0:T})=p_0^\theta(x_0)f_t^\theta(y_0|x_0)\prod_{t=1}^Tf_t^\theta(y_t|x_t)p^\theta(x_t|x_{t-1})

で与えられます．$\theta$はモデルのパラメータです．状態変数の初期値$X_0$が$p_0^\theta$から生成され，各$X_t$の値は１期前の値$X_{t-1}=x_{t-1}$に依存して$p_t^\theta$によって生成され，$t$期の観測値$Y_t$はその期の$X_t=x_t$の値を所与として$f_t^\theta$から生成される，という構造です．以下の模式図を見ると，背後で観測されない$X_t$の過程が走っていて各$X_t=x_t$の値のもとで$Y_t$の値が生成される，ということがわかりやすいかと思います．

状態空間モデルに基づいた分析においては，（$\theta$の値を固定して）次に挙げる点について関心があります．

• フィルタリング（filtering）：$Y_{0:t}=y_{0:t}$を所与としたときの$X_t$の条件付き分布
• 状態の予測：$Y_{0:t}=y_{0:t}$を所与としたときの$X_{t+1}$の条件付き分布
• スムージング（smoothing）：$Y_{0:T}$を所与としたときの$X_{t}$の条件付き分布
• データの予測：$Y_{0:t}=y_{0:t}$を所与としたときの$Y_{t+1}$の条件付き分布
• 尤度の計算：$L_T(\theta)=\int p^\theta_T(y_{0:T},x_{0:T})dx_{0:T}$

フィルタリング密度，状態の予測密度，スムージング密度は積分の漸化式で表されます．状態空間モデルモデルのパラメータ$\theta$を推定したい場合には，最尤法の場合では上記の$L_T$を最大化する必要がありますが，尤度を計算するためにはこの$T+1$次元の積分を解く必要があります．ガウス線形モデルの場合にはカルマンフィルターによって解析的にこれらの分析を行うことができますが，一般の状態空間モデルについては解析的に解くことはできません．SMCではこれらの数量をパーティクルに基づいた近似で計算します．

例：SVモデル

本記事では状態空間モデルの例として，ファイナンス分野などでよく利用される確率的ボラティリティ変動モデル（stochastic volatility model, SVモデル）を取り上げます．まずSVモデルは次のように表記されます．

Y_t|X_t=x_t \sim N(0,\exp(x_t)), \quad X_0\sim N(\mu, \sigma^2/(1-\rho^2)),\quad X_t|X_{t-1}=x_{t-1}\sim N(\mu+\rho(x_{t-1}-\mu),\sigma^2). 

ファイナンスでは$Y_t$は資産の（例えば日次の）対数収益などを表し，平均がゼロ，分散が$\exp(X_t)$の正規分布に従います．$X_t$はいわゆる対数ボラティリティ（分散の対数）で，平均$\mu$のAR(1)過程に従っており，初期分布はこのAR過程に基づいたものになります．$Y_t$と$X_t$の条件付き分布は両方とも正規分布ですが，$Y_t$の条件付き分散に指数関数が入っているので非線形モデルになっています．

パーティクルフィルター

パーティクルフィルターは状態変数のシミュレーションを行うことで関心のある数量を逐次的に近似します．冒頭でも言及したように，パーティクルフィルターはたくさんの状態変数をシミュレートし，それらに対してリサンプリング，値の更新，重みの計算を繰り返し，フィルタリング分布を代表するようなパーティクルが残るようにします．ここではパーティクルフィルター（bootstrapフィルター）の擬似コードだけを紹介しておきます．パーティクルを$X_t^n$，対応するパーティクルの重みを$w_t^n$，正規化された重みを$W_t^n$と表記します（$ n=1,\dots,N, t=1,\dots,T$）．

1. 初期化（$n=1,\dots,N$）：パーティクル$X_0^n$を初期分布から生成，ウェイトを作成$w_0^n=f_0(y_0|X_0^n)$，正規化する$W_0^n=w_0^n/\sum_{m=1}^Nw_0^m$．
2. $t=1,\dots,T$について次のステップを繰り返す：
   1. もし$ESS(W_{t-1}^{1:N})<ESS_{\min}$であれば，パーティクルのインデックス（$A_t^{1:n}$）を重み$W_{t-1}^{1:N}$に基づいてリサンプリングし，$\hat{w}^n_t=1$とする．そうでなければパーティクルのセットを引き続き使う（$A_t^n=n$，$\hat{w}^n_t=w^n_{t-1}$）
   2. パーティクル$X_t^n$の値を$p^\theta_t(x_t|x_{t-1}^{A_t^n})$の分布から生成して更新する．
   3. 重みを計算する：$w_t^n=\hat{w}_t^n f_t^\theta(y_t|X_t^n)$
   4. 重みを正規化する：$W_t^n=w_t^n/\sum_{m=1}^Nw_t^m$

$ESS$は有効サンプルサイズで，これが小さくなるとごく少数のパーティクルが大きな重みを持っている状態になるので，あらかじめ設定した$ESS_{\min}$を下回った場合にパーティクルのリサンプリングを行います．
パーティクルフィルターのアウトプットを使って，$t$期のフィルタリング分布は経験分布$\sum_{n=1}^N W_t^n\delta_{X_t^n}$で近似されます．また，フィルタリング分布についての$\varphi(X_t)$の期待値は$\sum_{n=1}^NW_t^n\varphi(X_t^n)$，$t$期のデータの周辺条件付き分布$L_t=f_t(y_t|y_{0:t-1})$は$\sum_{n=1}^Nw_t^n/\sum_{n=1}^N w_{t-1}^n$で近似できます（リサンプリングした場合には$N^{-1}\sum_{n=1}^Nw_t^n$）．またスムージングもパーティクルフィルターのアウトプットを使って近似することができます．

Bootstrapフィルターではパーティクルの値を更新するときに状態方程式の分布から生成していますが，より効率的にするために提案分布を使うこともできます（guidedパーティクルフィルター）．

particlesパッケージ

前置きが長くなりましたが，ここからパッケージの使用について紹介します．

導入

パッケージのインストールはpipなどでできます．またパッケージのドキュメンテーションはこのページにあります．このパッケージについて詳しく知りたい方はぜひ読んでみてください．githubのレポジトリには，本の中で紹介されている数値例に関するコードやデータセットが含まれています．

モデルの定義と人工データ生成

パッケージの準備ができたら，標準的なライブラリと一緒にパッケージ内のモジュールをインポートします．ここではstate_space_models，distributions，Momentsというそれぞれ状態空間モデルと確率分布を扱うモジュールとフィルタリング分布のモーメントを計算するモジュールをインポートしています．

import numpy as np
from matplotlib import pyplot as plt
import particles
from particles import state_space_models as ssm # 状態空間モデルを扱うモジュール
from particles import distributions as dists # 確率分布を扱うモジュール
from particles.collectors import Moments # フィルタリング分布のモーメントを計算するモジュール

次にモデルのクラスを定義します．ここでは上記のSVモデルを定義しています．

class StochVol(ssm.StateSpaceModel):
    default_params = {'mu': -1.0, 'rho': 0.9, 'sigma': 1.0 }
    # X_0の初期分布    
    def PX0(self):
        sig0 = self.sigma/np.sqrt(1.0-self.rho**2)
        return dists.Normal(loc=self.mu, scale=sig0)
    # X_t|X_{t-1}の分布
    def PX(self, t, xp):
        return dists.Normal(loc=self.mu + self.rho * (xp-self.mu), scale=self.sigma)
    # Y_t|X_tの分布
    def PY(self, t, xp, x):
        return dists.Normal(scale=np.exp(0.5*x))

このクラスの属性はモデルのパラメータの値（mu, rho, sigma）で，このクラスは３つのメソッド（PX0, PX, PY）が含まれています．３つのメソッドはそれぞれ$p_0^\theta(x_0)$，$p_t^\theta(x_t|x_{t-1})$，$f_t^\theta(y_t|x_t)$に対応する確率分布の記述となります．PX内のxpは$x_{t-1}$に対応し，PY内のxは$x_t$に対応します．ここで利用可能な確率分布はdistributionsモジュールに関するドキュメンテーションに記載されています．このモジュールでは

• 対数密度の評価（logpdfメソッド）
• 乱数の発生（rvsメソッド）
• 分位点の計算（ppfメソッド）

ができます．

クラスを定義したら，パラメータの値を自分で設定してインスタンス化して，データをモデルから生成します．データの生成にはインスタンスに対してsimulateメソッドを適用します．

my_sv_model = StochVol(mu=-11.0, rho=0.9, sigma=0.5) #インスタンス化

np.random.seed(seed=31)

T    = 200 # データ数
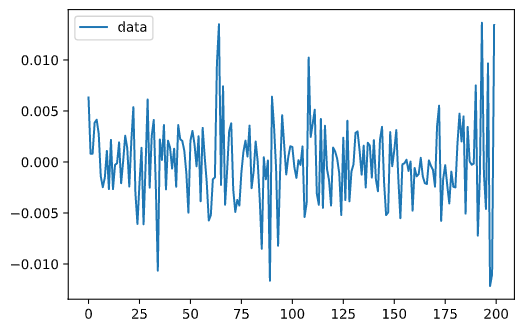
x, y = my_sv_model.simulate(T) # モデルからデータを生成
plt.plot(y, label='data')
plt.legend()

以下が生成したデータ$Y_t$のプロットになります．

フィルタリング

ではパーティクルフィルターを適用します．

N = 200 # パーティクルの数

fk_my_sv = ssm.Bootstrap(ssm=my_sv_model, data=y) # 状態空間モデルをFeynmanbootstrapフィルターを適用する
alg      = particles.SMC(fk=fk_my_sv, N=N, collect=[Moments()]) # SMCオブジェクトを作成
alg.run() # アルゴリズムをT期まで実行

まず定義した状態空間モデルからFeynman–Kacモデルに基づいたFeynmanKacオブジェクト（ssm.Bootstrapはこれのサブクラス）を作成します．この本ではより一般的なFeynman–Kacモデルに対するSMCを紹介しており，particlesパッケージでもFeynman–Kacモデルに対する適用がなされます．引数ssmには先程のSVモデルのインスタンスを，dataには観測データyを指定します．particles.SMCの引数fkには作成したFeynmanKacオブジェクト，Nにはパーティクル数を指定しています．一般的には

alg = particles.SMC(fk=fk_guided, N=100, qmc=False, resampling='systematic', ESSrmin=0.5,
                    store_history=False, verbose=False, collect=None)

となっており，疑似モンテカルロの使用（qmc），リサンプリングの条件（ESSrmin)，経過の保存（store_history，スムージングで使用），モーメントの計算（collect）など設定できます．

algオブジェクトはに対してrunメソッドを使うと，$T$期まで一気にフィルタリングを行います（ stepメソッドでは１期づつフィルタリングを進めていきます，step自体イテレータ）．このとき，algオブジェクトの属性は

• alg.t：次のイタレーションのインデックス
• alg.X：パーティクル$X_t^{1:N}$の値
• alg.W： パーティクルの重み$W_t^{1:N}$
• alg.Xp： １期前のパーティクルの値$X_{t-1}^{1:N}$
• alg.A： パーティクルの祖先，A[3]=12は$X_t^3$の親を意味，
• alg.summaries：ESS（ESSs），リサンプリングのフラグ（rs_flags），データの対数周辺条件付き分布（logLts）の履歴

などがあります．この属性にあるとおり，runでデータを全部使ってフィルタリングを行うと，store_historyがFalseの場合にはパーティクルの情報は最終時点$T$の状態しか残りません．よってcollectにモーメントを計算する関数を指定してモーメントの履歴を保存します（また，いちいち履歴をさかのぼってモーメントを計算するより便利です）．上の適用例ではMomentsの引数に何も指定していないのでフィルタリング分布の平均と分散を計算します．モーメントの値はalg.summaries.momentsに辞書型で保存されます．

フィルタリングの結果（フィルタリング分布の平均）を以下に図示します．

plt.plot(x, label='true state', color='k', ls=':')
plt.plot([m['mean'] for m in alg.summaries.moments], label='filtered mean')
plt.legend()

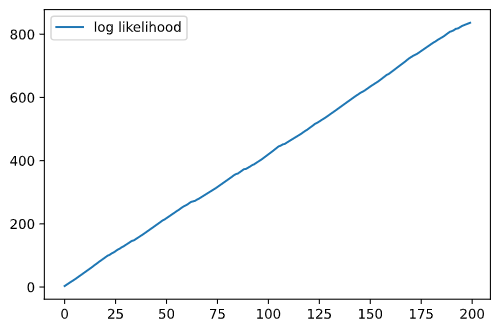
$\log L_t$のプロットも作成してみます．

plt.plot(alg.summaries.logLts, label='log likelihood')
plt.legend()

最初のフィルタリングの結果の図ですが，図としてちょびっと寂しい気がするので，フィルタリング分布の2.5%と97.5%の区間も追加してみたいと思います．自分で定義した関数をcollectに指定することも可能です．分位点を計算するnp.percentileは重みを入れることができないので，このページの関数を参考に，フィルタリング分布の平均，2.5%，97.5%点を計算する関数を作成しました．

def alternative_moments(W, X):
    # https://stackoverflow.com/questions/21844024/weighted-percentile-using-numpy
    X = np.array(X)
    quantiles = np.array([0.025, 0.975])
    if W is None:
        W = np.ones(len(X))
    W = np.array(W)
    assert np.all(quantiles >= 0) and np.all(quantiles <= 1), \
        'quantiles should be in [0, 1]'
    sorter = np.argsort(X)
    X = X[sorter]
    W = W[sorter]
    weighted_quantiles = np.cumsum(W) - 0.5 * W
    weighted_quantiles /= np.sum(W)
    
    res = np.interp(quantiles, weighted_quantiles, X)
    return {'mean': np.average(X, weights=W), '2.5%': res[0], '97.5%': res[1]}

この関数を以下のように指定することで各期の平均と分位点を保存することができます．

# mom_funcにalternative_momentsを指定
alg = particles.SMC(fk=fk_my_sv, N=N, collect=[Moments(mom_func=alternative_moments)], store_history=True)
alg.run()

plt.plot(x, label='true state', color='k', ls=':')
plt.plot([m['mean'] for m in alg.summaries.moments], label='filtered mean')

q1 = np.array([m['2.5%'] for m in alg.summaries.moments])
q2 = np.array([m['97.5%'] for m in alg.summaries.moments])
qq = np.concatenate([q1,q2[::-1]])
s  = np.arange(0,T)
tt = np.concatenate([s,s[::-1]])
plt.fill(tt, qq, color='b', alpha=0.2)
plt.legend()

ちなみに以下でスムージングを行うのでstore_historyをTrueにしています．このコードでは以下の図をプロットします．陰の部分がフィルタリング分布の2.5%から97.5%の区間になります．

スムージング

下記のコードは，パーティクルフィルターの結果（フィルタリングの際にstore_history=Trueとすること）を使って後ろ向きにパーティクルのトラジェクトリーを発生させていくforward filtering backward sampling（FFBS）の適用例です．フィルタリングの履歴alg.histにbackward_samplingを適用します．引数には

• M：トラジェクトリーの数（スムージングでのモンテカルロサンプルの数）
• linear_cost：Trueにすることで計算量$O(T(M+N))$の棄却FFBSを適用（棄却サンプリングにおけるバウンドをモデル内で指定する必要あり），Falseで通常のFFBSを実行（計算量は$O(TMN)$）

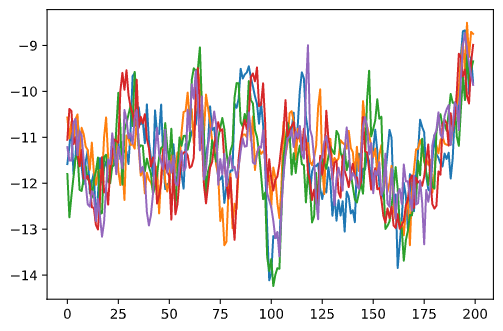
例えば，M=5の場合のトラジェクトリーは以下のようになります．

#トラジェクトリーの数は5，通常のFFBSを使用
trj = np.array(alg.hist.backward_sampling(M=5, linear_cost=False)) 
plt.plot(trj)

以下がM=Nの場合の結果です．FFBSの各トラジェクトリーは独立に生成されるので，スムージング分布の平均は単純に各時点における標本平均を計算しています．おまけとして2.5%と97.5%の区間もプロットしています．

trj = np.array(alg.hist.backward_sampling(N, linear_cost=False))
plt.plot(x, label='true state', color='k', ls=':')
plt.plot(np.average(trj, axis=1), label='smoothed mean')
q1  = np.percentile(trj, 2.5, axis=1)
q2  = np.percentile(trj, 97.5, axis=1)
qq = np.concatenate([q1,q2[::-1]])
s  = np.arange(0,T)
tt = np.concatenate([s,s[::-1]])
plt.fill(tt, qq, color='b', alpha=0.2)
plt.legend()

最後に

このパッケージは状態空間モデルを定義すればあとはフィルタリングやモデルのベイズ推定を簡単に行うことができます．本記事の実装例に対するパーティクルフィルターやスムージングは驚くほど速く動作します．状態空間モデルは時系列データ分析においてとても重要なので，このパッケージはとても有用なものであると思います．本自体もかなりしっかり書かれていてとても勉強になります．本記事ではパラメータの値を固定した状態でのフィルタリングやスムージングを行いましたが，現実の分析ではパラメータの値は推定します．次の記事では，このパッケージを使ったパラメータのベイズ推定を取り上げます．

米倉先生の記事でも書かれていたように，ビジネスにおいても時系列データはちゃんと時系列モデルに基づいた分析をするべきです．本記事で紹介した状態空間モデルの枠組みは，例えば売上高と広告費が毎日観測されていて，広告費にどれほど支出すると売上高がどの程度になるかを予測したい，といった場合に利用できます．このとき，時間とともに変化する広告費あるいはアドストックの効率性や一週間・一ヶ月周期で変化する要因などを観測されない状態変数として組み込むことが考えられます．また一週間にあるSKUに対する注文が何個分入るのかの分析・予測を行う際にも同じようにモデルを立てることができます．本記事で紹介したような既存のパッケージをベースとしたビジネスデータ活用分析支援・分析システム開発支援も行っておりますのでお問い合わせください．

一緒にお仕事しませんか！
株式会社Nospareではベイズ統計学に限らず統計学の様々な分野を専門とする研究者が所属しており，新たな知見を日々追求しています．統計アドバイザリーやビジネスデータの分析につきましては弊社までお問い合わせください．インターンや正社員も随時募集しています！