[Python]particlesパッケージで逐次モンテカルロ法を適用してみた（中編）

こんにちは，株式会社Nospare・千葉大学の小林です．前回の記事ではparticleパッケージを使ったパーティクルフィルターとスムージングの実装を行いました．今回はこのパッケージを使った状態空間モデルのパラメータ推定を紹介したいと思います．状態空間モデルは観測されるデータ$Y_t, (t=0,\dots,T)$と観測されない状態変数$X_t, (t=0,\dots,T)$からなる時系列モデルです．$X_t$はマルコフ過程に従い，$Y_t$は$X_t$を所与として条件付き独立です．密度関数を$p_0^\theta(x_0)$，$X_t$の条件付き密度を$p_t^\theta(x_t|x_{t-1})$，$Y_t$の条件付き密度を$f_t^\theta(y_t|x_t)$とすると，同時密度は

p^\theta_T(y_{0:T},x_{0:T})=p_0^\theta(x_0)f_t^\theta(y_0|x_0)\prod_{t=1}^Tf_t^\theta(y_t|x_t)p^\theta(x_t|x_{t-1})

で与えられます．$\theta$はモデルのパラメータです．あと状態変数をすべて積分消去して得られる尤度関数を

L_T(\theta)=\int p_T^\theta(y_{0:T},x_{0:T})d x_{0:T}

と書きます．

パラメータのベイズ推定

今までは状態空間モデルのパラメータの値を（真値に）固定してフィルタリングやスムージングを行ってきました．通常の分析ではパラメータの値は未知なので推定する必要があります．最尤法ではパーティクルフィルターの結果から$\log L_T(\theta)=\sum_{t=0}^T\log L_t$を近似できるので，これを$\theta$について最大化します．一方でベイズ推定ではパラメータ$\theta$に事前分布を仮定し，例えばマルコフ連鎖モンテカルロ法（MCMC）を使って

1. $X_{0:T}$を条件付き事後分布からサンプリングする
2. $\theta$を条件付き事後分布からサンプリングする

を繰り返すことで事後分布を得ることができます．状態変数のサンプリングは$X_t$を$t$ごとあるいはブロックにわけてサンプリングすることができます．

このアプローチはデータ拡大法（data augmentation）として見て取れます．条件付き分布が比較的簡単なものになることでサンプリングが容易になる一方で，状態変数が事後分布において依存性が高い場合にはMCMCが非効率になることが知られています．ある意味理想的（でも実行不可能）なMCMCサプリングの方法は$\theta$の事後分布

p(\theta|y_{0:T})\propto L_T(\theta)p(\theta)=\int p_T^\theta(y_{0:T},x_{0:T})d x_{0:T}p(\theta)

から直接サンプリングする方法です（ここで$p(\theta)$は事前密度）．この方法は状態変数の影響がないので上のMCMCよりも効率的であることが期待できます．この場合のMetropolis-Hastings(MH)アルゴリズムの採択確率は次のようになります：

\min\left\{1, \frac{L_T(\theta^*)p(\theta^*)q(\theta|\theta^*)}{L_T(\theta)p(\theta)q(\theta^*|\theta)}\right\}.

ここで，$\theta^*$は提案されたパラメータの値，$\theta$は現在のパラメータの値，$q(\cdot|\cdot)$は提案密度です．$L_T(\theta)$が解析的に得られないのでこのMHアルゴリズムは直接実行することはできませんが，$L_T$をSMCで得られる不偏推定量$\hat{L}$に置き換えてMHアルゴリズムを実行するとちゃんと$\theta$の事後分布からのサンプリングが行えるということが知られています．このように，ターゲット密度をその不偏推定量で置き換える方法は一般的にpseudo-marginalアプローチと呼ばれ，その中でパーティクルフィルターによって不偏推定量を構築してするMHアルゴリズはparticle marginal MH（PMMH）アルゴリズムと呼ばれます（particle Gibbsという手法もあり，これらの手法を総称してparticle MCMCと呼びます）．

PMMHの実装

particlesパッケージではPMMHやparticle Gibbsを実行して状態空間モデルのパラメータのベイズ推定を行うことができます．
今回はlocal trend model

y_t = x_t + e_t,\\ 
x_t=x_{t-1} + v_t

を取り上げます．ここで$e_t\sim N(0,\sigma^2)$, $v_t\sim N(0,\tau^2)$, $x_1\sim N(x_0,\tau^2)$で，モデルパラメータは$x_0$, $\sigma^2$, $\tau^2$です．
まずモデルの定義とインスタンス化，データの発生を行います．

import numpy as np
from matplotlib import pyplot as plt
import particles
from particles import state_space_models as ssm # 状態空間モデルを扱うモジュール
from particles import distributions as dists # 確率分布を扱うモジュール

class LocalTrend(ssm.StateSpaceModel):
    default_params = {'x0': 0.0, 'sigma2': 1.0, 'tau2': 1.0 }
    # X_0の初期分布    
    def PX0(self):
        return dists.Normal(loc=self.x0, scale=np.sqrt(self.tau2))
    # X_t|X_{t-1}の分布
    def PX(self, t, xp):
        return dists.Normal(loc=xp, scale=np.sqrt(self.tau2))
    # Y_t|X_tの分布
    def PY(self, t, xp, x):
        return dists.Normal(loc=x, scale=np.sqrt(self.sigma2))

# 真値
true_par = {'x0':0, 'sigma2':1, 'tau2':0.1}
#インスタンス化
my_LT_model = LocalTrend(x0=true_par['x0'], sigma2=true_par['sigma2'], tau2=true_par['tau2'])

np.random.seed(11)
T    = 200 # データ数
x, y = my_LT_model.simulate(T) # モデルからデータを生成
fig = plt.figure(figsize=(10, 6))

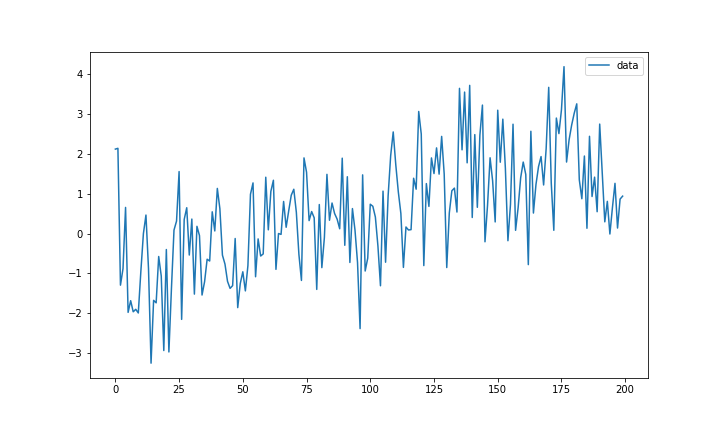
$x_0=0$, $\sigma^2=1$, $\tau^2=0.1$で発生させたデータはこんな感じです．

次にパラメータの事前分布$x_0\sim N(0,1)$, $\sigma^2\sim IG(0.1,0.1)$, $\tau^2\sim IG(0.1,0.1)$を以下のように設定します．

prior_dict = {'x0': dists.Normal(loc=0.0, scale=1.0), 'sigma2': dists.InvGamma(a=0.1, b=0.1), 'tau2': dists.InvGamma(a=0.1, b=0.1)}
my_prior   = dists.StructDist(prior_dict)

PMMHを使うためにはmcmcモジュールをインポートする必要があります．

from particles import mcmc

draw = 5000

# PMMHクラスをインスタンス化
my_pmmh = mcmc.PMMH(ssm_cls=LocalTrend, data=y, prior=my_prior, Nx=T, niter=draw) 
my_pmmh.run()

mcmc.PMMHの引数は例えば

• niter：MCMCの長さ（整数）
• ssm_cls：StateSpaceModelクラス
• smc_cls：SMCクラス，デフォルトでparticles.SMC
• prior：事前分布
• data：データ
• Nx：パーティクルフィルターのパーティクル数
• theta0：MCMCのパラメータの初期値（デフォルトでは事前分布から発生させる）
• adaptive：Trueで適応的MHを行う（デフォルトでTrue）

などがあり，上のコードではssm_clsとpriorには上で定義したlocal trend modelLocalTrendとmy_prior，Nxには観測数と同じパーティクル数Tを指定しています．パーティクルフィルターのときと同じようにrunメソッドでアルゴリズムを実行します．
イタレーションごとにパーティクルフィルターを実行するのでちょっと時間がかかります．自分の環境では5000回の繰り返しで3分半ほどかかりました．

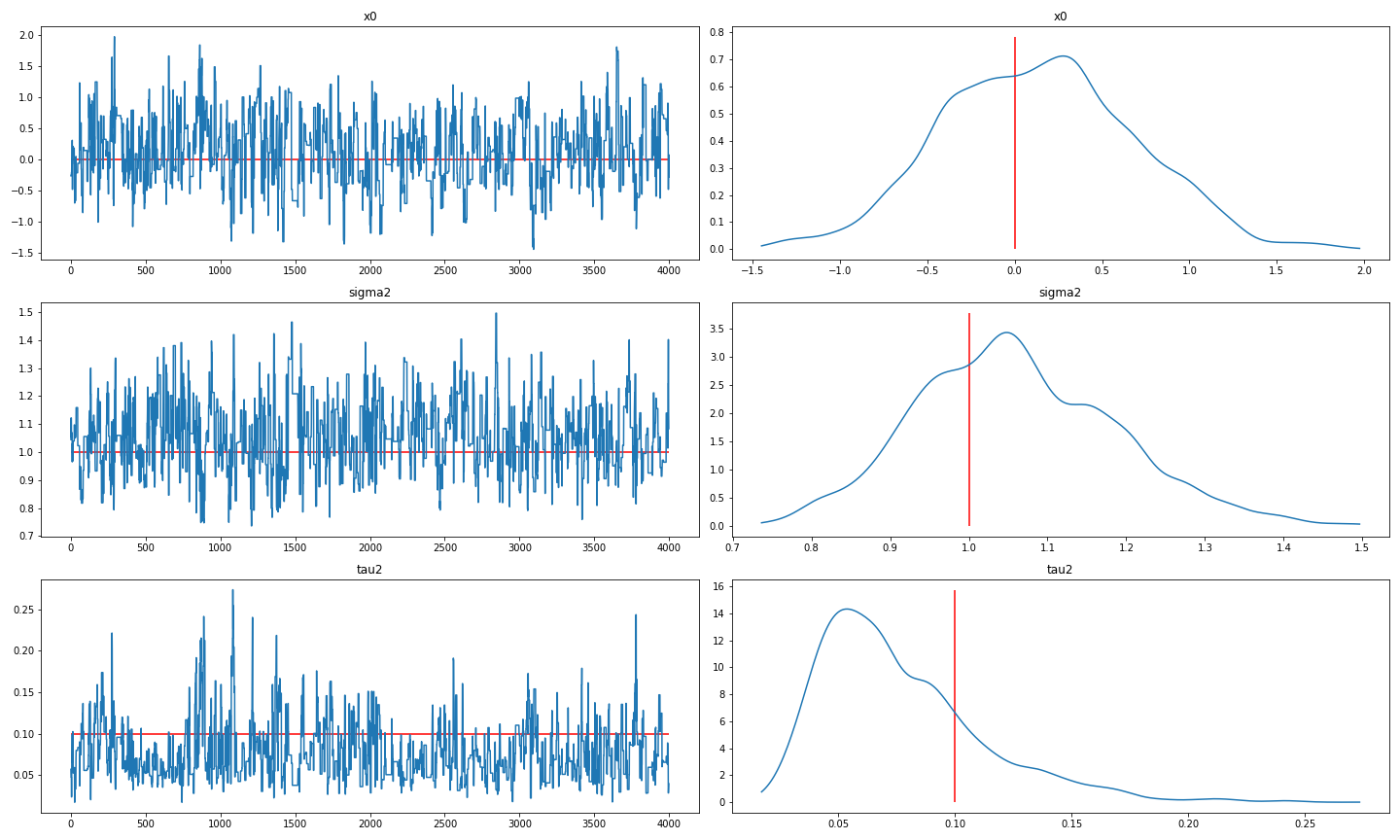
PMMHのサンプリング結果をトレースプロットと事後密度として図示します．

# burn-in
burn = 1000
fig = plt.figure(figsize=(20, 12))
for i, p in enumerate(prior_dict.keys()):
    ax  = fig.add_subplot(3,2,2*i+1)
    ax.plot(my_pmmh.chain.theta[p][(burn + 1):], label='')
    ax.hlines(true_par[p], 0, draw-burn-1, colors='red')
    plt.title(p)

    ax  = fig.add_subplot(3,2,2*i+2)
    tmp = my_pmmh.chain.theta[p][(burn + 1):]
    dens = kde.gaussian_kde(tmp)
    x = np.linspace(tmp.min(), tmp.max(),300)
    y = dens(x)
    plt.plot(x,y, label='PMMH')
    ax.vlines(true_par[p], 0, 1.1*max(y), colors='red')
    plt.title(p)

fig.tight_layout()

真値を赤い線で表していますが，ちゃんとPMMHアルゴリズムは真値周辺に収束してサンプリングを行うことができているようです．$x_0$, $\sigma^2$, $\tau^2$の95%信用区間はそれぞれ[-0.903, 1.207]，[0.823, 1.332]，[0.030, 0.164]で真値を含んでいます．

今回はガウス線形状態空間モデルなので，状態変数もサンプリングするMCMCの適用も簡単に行うことができます．ここでは状態変数を積分除去することでPMMHがどれだけ効率性がよくなるか（自己相関が下がるか）を見るために，次のふたつの状態変数をサンプリングするMCMCを考えます．

• シングルムーブサンプラー：$X_t|X_{-t},\theta$を$t=1,\dots,T$についてサンプリングする
• 前向きフィルタリング後ろ向きサンプリング（FFBS）：カルマンフィルターで前向きにフィルタリングを行い，スムージング分布から$X_t$を後ろ向き（$t=T,\dots,1$の順）に逐次的にサンプリングする．

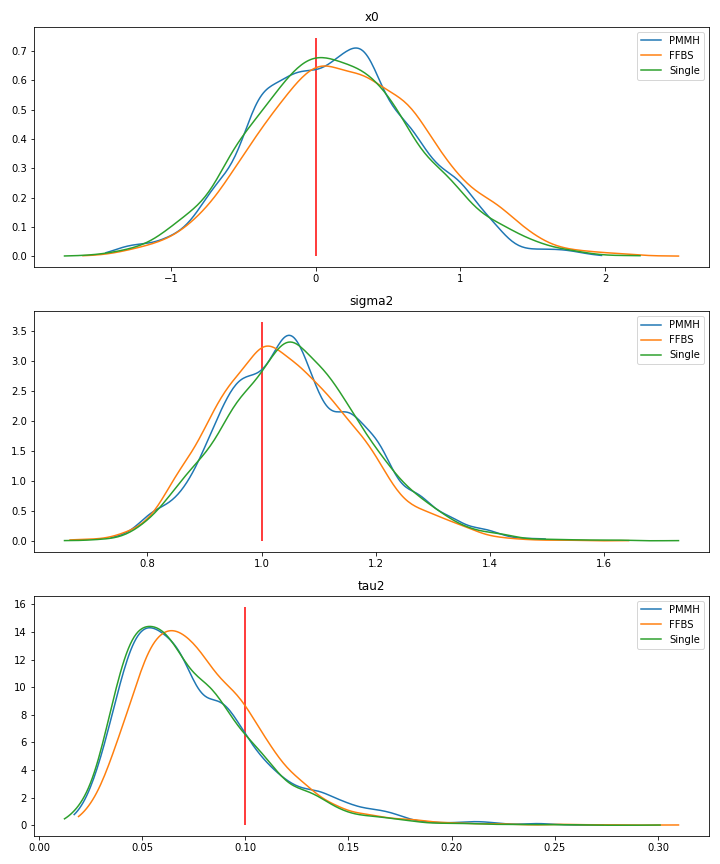
これらの２つのアルゴリズムはRで適用しましたが，同じ5000回の繰り返しでも２つ合わせて数秒で計算は終わりました．まず先に各アルゴリズムから得られた事後分布のプロットを見てみると３つのアルゴリズムで同じような結果になっています．．

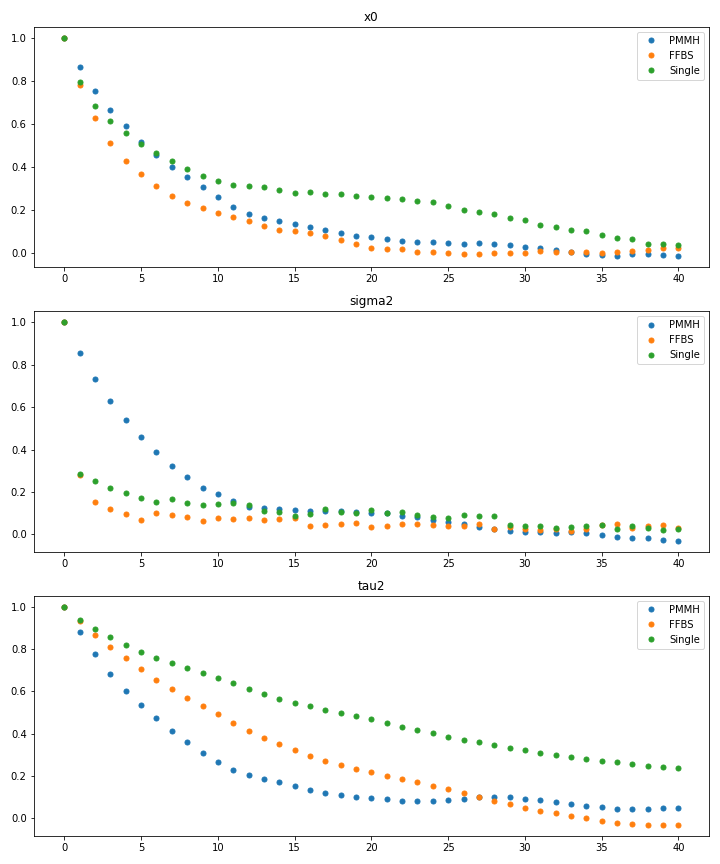
次にさて自己相関関数を見てみましょう．

状態変数を１つずつサンプリングするシングルムーブは$x_0$と特に$\tau^2$で自己相関の減衰が遅くなっています．一方でPMMHは$\tau^2$の自己相関の減衰がFFBSとシングルムーブと比べて早くなっていて$_0$についてはFFBSと同等のようです．$\sigma^2$についてはFFBSとシングルムーブのほうが早くなっています．

おわりに

今回の記事の数値例では単純な線形ガウス状態空間モデルを取り上げましたが，PMMHはもっと複雑な状態空間モデルのパラメータを効率的に推定するために適用することができます．ただしやはりMCMCの各繰り返しでパーティクルフィルターを実行しなければならないので計算時間はかかってしまうようです．

株式会社Nospareではベイズ統計学に限らず統計学の様々な分野を専門とする研究者が所属しており，新たな知見を日々追求しています．統計アドバイザリーやビジネスデータの分析につきましては弊社までお問い合わせください．インターンや正社員も随時募集しています！