はじめに
この記事は、私が機械学習、特に「誤差逆伝播法」 (あるいは「バックプロパゲーション (Backpropagation)」) を勉強するうえで辿った道筋を記録しておくものです。
誤差逆伝播法に関する分かりやすい解説は、ここ Qiita にも多数存在しますので、正直 $n$ 番煎じなところがありますが、あくまで記録ですのでここは 1 つ。
「記録」というには長過ぎてイマイチ感溢れてますが、そこは気にしないでください。これでも要点をしぼったつもりなのです…![]()
ゆっくりしていってね!!!
途中の数式について
記事の前後から参照されている数式については右側に番号を振っています。
初回記載時は $\text{(1)}$ とかっこ付き数字で、2 回目以降記載時は $\text{[1]}$ と角かっこ付き数字で示します。記載済みの数式を変形したものについては $\text{(1')}$ とプライム付き数字で示します。
番号が振られていない数式は、前後から参照されなかったことを示すだけで、その式の重要性が低いことを表すものではありません。
誤差逆伝播法の屋台骨
誤差逆伝播法は、「連鎖律 (chain rule)」1 という定理と「最急降下法 (gradient descent)」というアルゴリズムの 2 つによって支えられています。
連鎖律
「連鎖律」とは、複数の関数が組み合わさった 合成関数 を微分する際のルールのことです。
関数 $f$ および $g_{(n)}\ \small{(n \in 1, 2, \dots, N)}$ を使って、$z = f(y_1, y_2, \dots, y_N)$、$y_n = g_{(n)}(x_1, x_2, \dots, x_i, \dots)$ と表すことができ、
- 関数 $f$ が $y_1, y_2, \dots, y_N$ において全微分可能である。
- 関数 $g_{(n)}$ がそれぞれ $x_i$ について偏微分可能である。
の 2 つを満たすとき、以下の $\text{(1)}$ が成り立ちます。
\begin{align}
\frac{\partial z}{\partial x_i} &= \frac{\partial z}{\partial y_1}\cdot\frac{\partial y_1}{\partial x_i} + \frac{\partial z}{\partial y_2}\cdot\frac{\partial y_2}{\partial x_i} + \cdots + \frac{\partial z}{\partial y_N}\cdot\frac{\partial y_N}{\partial x_i} \\
&= \sum_{n=1}^{N} \frac{\partial z}{\partial y_n}\cdot\frac{\partial y_n}{\partial x_i}
\end{align} \tag{1}
いきなり一般化された式が出てきて難しく感じるかもしれませんが、イメージとして以下のように覚えておくとよいかと思います。
- 変数が中継する (例えば $z$ → $y_1$ → $x_i$) 場合、偏微分は各々の 積 で表す。
- 変数が複数に分岐する ($z$ → $y_1, y_2, \dots, y_N$) 場合、偏微分は各々の 和 で表す。
ちなみに関数 $f$ と $g_{(n)}$ がどちらも 1 変数関数の場合、連鎖律は積のルールだけが残って非常に簡単に表すことができます。
\frac{dz}{dx} = \frac{dz}{dy}\cdot\frac{dy}{dx}
「合成関数の微分」として、高校数学の数Ⅲで習った方も多いのではないでしょうか。$y = \log(\sin^2x)$ を微分せよ、とか。
なお、連鎖律は既に証明されているものですので、この記事ではありがたく使わせていただき、証明は割愛しますが、例えば東大の清野先生が行っているゼミの資料でかなり丁寧に証明を解説されていますので、参考にしてみてください。
最急降下法
「最急降下法」は、関数 $f(\boldsymbol{x})$ が最小値をとるときの変数 $\boldsymbol{x}$ の値を、関数の微分、つまり 1 階導関数のみを使って求めるアルゴリズムの 1 つです。
関数の最小値あるいは最大値を求める問題を「最適化問題」とよびますが、その中でも最急降下法は、問題を解くために導関数が必要な「勾配法」のカテゴリーに属します。
\begin{align}
\boldsymbol{x}^{(k+1)} &= \boldsymbol{x}^{(k)} - \eta \frac{\partial}{\partial \boldsymbol{x}^{(k)}} f(\boldsymbol{x}^{(k)}) \\
&= \boldsymbol{x}^{(k)} - \eta \begin{bmatrix}
\dfrac{\partial f(\boldsymbol{x}^{(k)})}{\partial x_1^{(k)}} \\
\dfrac{\partial f(\boldsymbol{x}^{(k)})}{\partial x_2^{(k)}} \\
\vdots \\
\dfrac{\partial f(\boldsymbol{x}^{(k)})}{\partial x_n^{(k)}}
\end{bmatrix}
\end{align} \tag{2}
$\boldsymbol{x}$ の右肩にあるかっこの中は反復の回数であり、$k$ 回目の値から、新しく $k+1$ 回目の値を求める漸化式になっています。
係数 $\eta$ (エータ) に特に名前は付いていませんが、機械学習でこのアルゴリズムが利用されるときは「学習率 (learning rate)」とよばれたりします。
既に $\text{(2)}$ から明らかですが、最急降下法における $\boldsymbol{x}$ の修正方針は以下の 2 点です。
- 微分係数の絶対値が大きいほど正解から離れていると判断して、より大胆に修正する (=修正量を大きくする)。
- 微分係数が傾きを表す性質から、微分係数の符号とは逆の方向に修正する。
これは $\boldsymbol{x}$ が 1 変数で、$f(\boldsymbol{x})$ が 2 次関数で下に凸だったときのグラフを思い浮かべてみると分かりやすいと思います。2
$\boldsymbol{x}$ が多変数、つまりベクトルになっても考え方は同じで、$f(\boldsymbol{x})$ に平面・超平面的な “くぼみ” が存在すれば、そこに落ち着いていくことになります。
ただし、個々の変数を修正するためには $x_1, x_2, \dots, x_n$ それぞれの値の変化に対する $f(\boldsymbol{x})$ の増減に注目する必要が生じるため、式は偏微分になっているわけです。
非常にシンプルで分かりやすいアルゴリズムですが、注意するべき点もあります。
- $\boldsymbol{x}$ が収束したとしても、そのときの $f(\boldsymbol{x})$ が最小値であるとは限らない。
- 例えば 4 次関数のように “くぼみ” が複数箇所存在する場合、最小ではない “くぼみ” にハマって抜け出せなくなり、その中の最小値 (つまり極小値) を解と勘違いすることが起こりうる。
- このように、問題が解けているように見えて実は正解 (大域的最適解) ではない解を局所的最適解という。
- 収束スピードが導関数に依存しており、微分係数が 0 に近いと収束が きわめて 遅くなる。
- 勾配法のアルゴリズムは常にこの危険がつきまとい、「勾配消失問題 (vanishing gradient problem)」とよばれる。
- 係数 $\eta$ は大きすぎても小さすぎてもよくない。また、$f(\boldsymbol{x})$ およびその導関数によって最適な値は異なる。
- $\eta$ が大きいと発散・振動を起こす危険が高くなり、逆に小さいと収束が遅くなる。
- $\boldsymbol{x}$ の修正量は $\eta$ と微分係数によって決まるため、微分係数が大きすぎる・小さすぎるときの対策が必要な場合がある。
これらの注意点は、近年の研究によって改善したり、問題を起こさないようなパラメータ設定などが提案されていますが、ここでは誤差逆伝播法のコアの部分を取り上げたいので、あまり深く考えないことにします。
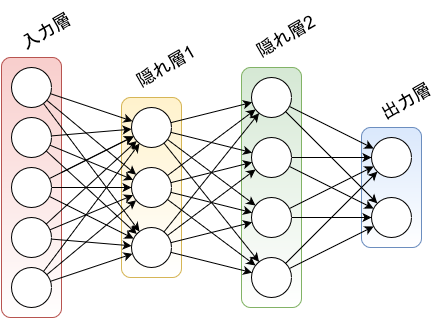
順伝播型ニューラルネットワーク
「順伝播型ニューラルネットワーク」 (あるいは「フィードフォワードニューラルネットワーク (feedforward neural network)」) は、以下を満たすニューラルネットワークのことです。
-
層状の ネットワークで、ノードのすべてが「層 (layer)」のいずれかに属する。
- ネットワークに入力されたデータを持つノードの層は「入力層 (input layer)」、前の層が持つ値を使って演算した結果を持つノードの層は「隠れ層 (hidden layer)」、隠れ層と同じく演算結果を持つノードの層で、ネットワークの最終にある層を「出力層 (output layer)」とよぶ。
- 隠れ層が複数あるネットワークや、逆に隠れ層を持たず、入力層と出力層しかないネットワークもある。
- すべてのノードは、隣接する層のノードとの間にのみ接続を持つ。同一層どうしの接続や、層をまたいだ接続はない。
言葉で書くとひたすらややこしいですが、要は下の図のような形をしたニューラルネットワークのことを指します。
出力層で我々の望んだ結果が出るようにパラメータを調整する作業が、ニューラルネットワークにおける「学習」です。
なおこれ以降、単に「ニューラルネットワーク」あるいは「ネットワーク」と書いた場合は、この「順伝播型ニューラルネットワーク」を指すことにします。
計算モデル
先ほど隠れ層の説明で、“前の層が持つ値を使って演算した結果を持つ” と書きました。
ニューラルネットワークにおいて、一般にこの演算は “前の層の値に係数を掛けて足し合わせる” というもので、以下の計算モデル $\text{(3)}$ で示されます。
\boldsymbol{l}^{(k+1)} = \sigma^{(k+1)}(\boldsymbol{W}^{(k+1)} \boldsymbol{l}^{(k)} + \boldsymbol{b}^{(k+1)}) \tag{3}
各記号の右肩にあるかっこの中は層の番号であり、$k$ 番目の層が持つ値 $\boldsymbol{l}^{(k)}$ から、$k+1$ 番目の層の値 $\boldsymbol{l}^{(k+1)}$ を求める漸化式になっています。
一番前の層、つまり入力層から始まり、この漸化式にしたがって出力層まで順番に計算していく過程を、「順伝播 (forward propagation)」といいます。順 があるからには 逆 もあるわけですが、それはのちほど。
$\boldsymbol{W}$ は前の層の各ノードから自分に対しての影響を表す値で、「重み (weight)」とよばれます。また、$\boldsymbol{b}$ は前の層のノードに影響しない “定数的な” 性格を持つ値で、「バイアス (bias)」とよばれます。
層は一般に複数のノードで構成されていますから、層のノードが持つ値 $\boldsymbol{l}$ を ベクトル で表すと、バイアス $\boldsymbol{b}$ はノードごとに持つ値ですので同じくベクトルとなり、重み $\boldsymbol{W}$ はベクトルからベクトルを求める変換ですので 行列 となります。
$\sigma$ は「活性化関数 (activation function)」とよばれ、重みとバイアスを使って求めた値 ($\boldsymbol{W} \boldsymbol{l} + \boldsymbol{b}$) に対する 何らかの変換 を行います。
古くはヘヴィサイドの階段関数 (Heaviside step function) だったり恒等写像 (identity function) だったりしましたが、現在は 何らかの非線形な関数 3 が使われます。
また、ネットワーク内のすべてで同じものを使う必要はなく、例えば隠れ層と出力層で異なる活性化関数を使うことができます。
ちなみに $\text{(3)}$ は、常に 1 を出力するノードを追加で用意し、バイアスをそのノードに対する重みとして考えることで、バイアス項を取り払うことができます。
\begin{align}
\boldsymbol{l'}^{(k)} &= \begin{bmatrix}
1 \\
\boldsymbol{l}^{(k)}
\end{bmatrix} = \begin{bmatrix}
1 \\
l_1^{(k)} \\
l_2^{(k)} \\
l_3^{(k)} \\
\vdots
\end{bmatrix} \\
\boldsymbol{W'}^{(k)} &= \begin{bmatrix}
\boldsymbol{b}^{(k)} & \boldsymbol{W}^{(k)}
\end{bmatrix} = \begin{bmatrix}
b_1^{(k)} & W_{11}^{(k)} & W_{12}^{(k)} & W_{13}^{(k)} & \cdots \\
b_2^{(k)} & W_{21}^{(k)} & W_{22}^{(k)} & W_{23}^{(k)} & \cdots \\
b_3^{(k)} & W_{31}^{(k)} & W_{32}^{(k)} & W_{33}^{(k)} & \cdots \\
\vdots & \vdots & \vdots & \vdots & \ddots
\end{bmatrix} \\
\\
\boldsymbol{l}^{(k+1)} &= \sigma^{(k+1)}(\boldsymbol{W'}^{(k+1)} \boldsymbol{l'}^{(k)}) \tag{3'}
\end{align}
書籍やウェブサイトによっては $\text{(3')}$ の形で書かれることもありますが、本質的には同じものです。
学習の戦略
先ほど書いたように、ニューラルネットワークにおける「学習」とは、出力層が正しい値となるように、パラメータ、すなわち 重み と バイアス を修正していく作業のことです。
誤差逆伝播法においては、ニューラルネットワークに対して「損失関数 (loss function)」 (あるいは「コスト関数 (cost function)」) という、簡単にいえば “出力層の値がどれだけ正しい状態、望まれている状態から離れているか” を表す関数を定めて、最急降下法を用いてこれを最小化する最適化問題に帰着させます。
なお、最適化問題の対象となる関数を「目的関数 (objective function)」とよぶため、そちらの名称が使われることもありますが、この記事では「損失関数」で統一します。
この記事では、学習に使うデータに、入力と、それに対して 望まれる出力 がセットで用意されている「教師あり学習 (supervised learning)」を取り上げます。
ただし誤解しないでいただきたいのですが、教師あり学習でなければ誤差逆伝播法を適用できないわけではありません。
誤差逆伝播法は、ネットワークの損失関数を定めることができ、その関数を使って重みとバイアスを修正できればよく、教師あり学習である必要はありません。
損失関数を立てる
話を戻して、教師あり学習は入力に対して “望まれる出力” (これを「教師信号 (supervisory signal)」といいます) を出せるよう、ニューラルネットワークを学習する方法ですが、当然ながら、学習を行っていない初期状態のネットワークの出力は、ふつう教師信号とは遠くかけ離れたものとなるはずです。
この “どれくらいかけ離れているか” をどうにかして式で表し、損失関数とするのですが、例えば分かりやすいものとして「2 次損失関数 (quadratic loss function)」 (あるいは「2 乗和誤差 (sum-of-squares error)」や「残差平方和 (residual sum of squares)」ともよばれます) があります。
\begin{align}
L &= (o_1 - T_1)^2 + (o_2 - T_2)^2 + \cdots + (o_N - T_N)^2 \\
&= \sum_{n=1}^N (o_n - T_n)^2 \\
&= \| \boldsymbol{o} - \boldsymbol{T} \|^2
\end{align} \tag{4}
ここで $\boldsymbol{o} = (o_1, o_2, \dots, o_N)$ はニューラルネットワークの出力層の値であり、$\boldsymbol{T} = (T_1, T_2, \dots, T_N)$ は教師信号です。$\|\cdots\|$ はベクトルのノルム 4 を表します。
教師信号との差の 2 乗和を損失とすることは、直感的にも理にかなったものであると思います。
2 乗したものを足していくわけですから、$L$ は必ず 0 以上になりますし、出力値と教師信号が離れれば離れるほど損失が大きいと判断されます。
そして、出力値と教師信号がぴったりと一致するときに損失は最小となり、$L$ は最小値 0 となります。
この損失関数 $L$ はネットワークの出力層の値 $\boldsymbol{o}$ を変数にとりますが、これはネットワーク内のすべての重みとバイアスによって計算された値ですから、つまるところ、$L$ はすべての重みとバイアスを変数にとることを意味します。
よって、$L$ に対するネットワーク内の任意の重み、バイアスの偏微分を求めることができれば、最急降下法を使うことで重みとバイアスを修正して、結果として損失関数を最小化することができるはずです。
ちなみに損失関数をうまく定めると、収束を早めたり、スパース性 5 を高めたりすることができますが、高度な内容となりますし、自分もまだ勉強が足りていないところですので、またいずれ。
すべての入力を考慮した損失関数
前節の $\text{(4)}$ で 2 次損失関数を紹介しましたが、このとき、出力値 $\boldsymbol{o}$ と教師信号 $\boldsymbol{T}$ は入力ごとに異なるものですから、損失関数も入力ごとに算出されます。
よって、2 次損失関数をもう少し正確に書けば、$k$ 番目の入力に対して、
\begin{align}
L^{(k)} &= (o_1^{(k)} - T_1^{(k)})^2 + (o_2^{(k)} - T_2^{(k)})^2 + \cdots + (o_N^{(k)} - T_N^{(k)})^2 \\
&= \sum_{n=1}^N (o_n^{(k)} - T_n^{(k)})^2 \\
&= \| \boldsymbol{o}^{(k)} - \boldsymbol{T}^{(k)} \|^2
\end{align}
と表すことができます。
ニューラルネットワークの重みとバイアスは、すべての入力に対して共通に使われるパラメータですから、個別の入力に対する損失関数ではなく、すべての入力を考慮した、いわばニューラルネットワークの「全体損失関数」6 が必要になります。
ここでは、入力の総数を $K$ として、各入力に対する損失関数 $L^{(k)}\ \small{(k \in 1, 2, \dots, K)}$ を使って全体損失関数 $L^{(all)}$ を求めてみましょう。
決め方は色々あると思いますが、難しく考える必要はありません。例えば各入力に対する損失関数の 総和 としてはどうでしょうか。
L^{(all)} = L^{(1)} + L^{(2)} + \cdots + L^{(k)} + \cdots = \sum_{k=1}^K L^{(k)} \tag{5}
2 次損失関数は $L^{(k)} \ge 0$ が成り立つわけですから、このようにしても問題はないわけです。
逆に、損失関数が負の値になることがあるなど、$\text{(5)}$ が適用できないケースがあるかもしれません。そのときは適切な立式が必要です。
さて、今回はこれで問題ないとして、いま、全体損失関数 $L^{(all)}$ をネットワーク内のとある重みもしくはバイアス $w$ で偏微分する、つまり $\partial L^{(all)}/\partial w$ を求めることを考えます。
まず、$L^{(all)}$ が各入力に対する損失関数 $L^{(k)}$ を変数にとることは $\text{(5)}$ から明らかです。
そして $L^{(k)}$ がネットワーク内のすべての重み、バイアスを変数にとることは前節で書きました。つまり $L^{(k)}$ は $k = 1, 2, \dots, K$ のそれぞれにおいて $w$ を変数にとります。
ここで「連鎖律」の出番がやってきます。$\text{(1)}$, $\text{(5)}$ から以下の $\text{(6)}$ を導くことができます。
\begin{align}
\frac{\partial L^{(all)}}{\partial w} &= \frac{\partial L^{(all)}}{\partial L^{(1)}}\cdot\frac{\partial L^{(1)}}{\partial w} + \frac{\partial L^{(all)}}{\partial L^{(2)}}\cdot\frac{\partial L^{(2)}}{\partial w} + \cdots + \frac{\partial L^{(all)}}{\partial L^{(K)}}\cdot\frac{\partial L^{(K)}}{\partial w} \\
&= \frac{\partial L^{(1)}}{\partial w} + \frac{\partial L^{(2)}}{\partial w} + \cdots + \frac{\partial L^{(K)}}{\partial w}\ \left( \because \frac{\partial L^{(all)}}{\partial L^{(k)}} = 1\ (k \in 1, 2, \dots, K) \right) \\
&= \sum_{k=1}^{K} \frac{\partial L^{(k)}}{\partial w}
\end{align} \tag{6}
計算は小難しく見えるかもしれませんが、出てきた結果はシンプルなもので、各入力ごとに損失関数から偏微分 ($\partial L^{(k)}/\partial w$) を求めて、それを合計すると全体の偏微分 ($\partial L^{(all)}/\partial w$) になることが分かりました。
ちなみに、この記事では全体損失関数は各入力に対する損失関数の 総和 としていますが、平均 を採用することもできます。
L^{(all)} = \frac{1}{K} ( L^{(1)} + L^{(2)} + \cdots + L^{(k)} + \cdots ) = \frac{1}{K} \sum_{k=1}^K L^{(k)}
これを同様に $w$ で偏微分すると、
\frac{\partial L^{(all)}}{\partial w} = \frac{1}{K} \sum_{k=1}^{K} \frac{\partial L^{(k)}}{\partial w}\ \left( \because \frac{\partial L^{(all)}}{\partial L^{(k)}} = \frac{1}{K} \right)
となり、各入力ごとの損失関数の偏微分の平均が、全体の偏微分となります。
平均をとるわけですから、総和 の全体損失関数を採用したときと比べて、最急降下法による修正量は小さくなります。しかしこれは係数 $\eta$ で調節できますので、これだけでどちらが有利・不利ということはいえません。
これ以降は、各入力に対する損失関数は単に $L$ として、$(k)$ を肩に乗せずに表すことにします。$\TeX$ 記法も長くなってしまいますしね。
誤差逆伝播法による学習の実例 - 半加算器
ここまでで必要な事前知識はすべて揃ったので、誤差逆伝播法の一般式を書いてもよいのですが、その前に単純な実例として、「半加算器 (half adder)」を学習させてみます。
あくまで実例ですし、不要な方は読み飛ばして…いただいてもよいのですが、誤差逆伝播法を一般化した式は一見すると非常に分かりづらい表記ですので、こちらにも目を通していただいたほうが理解は進むと思います。
概要とニューラルネットワークでの表現
半加算器は、2 つの入力 A, B を受け取り、以下の表にしたがって 2 つの出力 S, C を送り出す装置です。
もう少し踏み込んで言えば、2 つの入力 A, B が 1 であるものの数を、2 ビット CS で表す装置です。
| in A | in B | out S | out C |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
上の真理値表を見ると、S は A と B の 排他的論理和 ($S = A \veebar B$)、C は 論理積 ($C = A \wedge B$) として表せることがわかります。
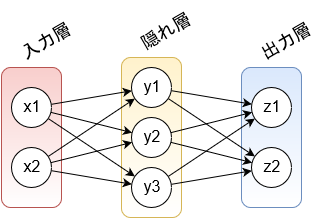
今回はこの半加算器を、入力層 2 次元 (A, B)、隠れ層 3 次元、出力層 2 次元 (S, C) の 3 層ニューラルネットワークで学習させてみましょう。7
隠れ層の次元数は、この記事では説明のために 3 次元にしていますが、興味があれば次元数を変えたときにどうなるのか、試してみてください。
各層の値の計算式ですが、$\text{(3)}$ では各層の値を $\boldsymbol{l}^{(k)}$ で表しましたが、この例では 3 層ですから、もっと簡単に、入力層を $\boldsymbol{x} = (x_1, x_2)$、隠れ層を $\boldsymbol{y} = (y_1, y_2, y_3)$、出力層を $\boldsymbol{z} = (z_1, z_2)$ と表すことにしましょう。
\begin{align}
\boldsymbol{x} &= (x_1, x_2) = \{ (0, 0), (0, 1), (1, 0), (1, 1) \} \tag{7} \\
\\
\boldsymbol{I_y} &= (I_{y_1}, I_{y_2}, I_{y_3}) = \boldsymbol{W_y} \boldsymbol{x} + \boldsymbol{b_y} \tag{8} \\
&\ \ \left|
\begin{array}{l}
\ I_{y_1} = W_{y_{11}} x_1 + W_{y_{12}} x_2 + b_{y_1} \\
\ I_{y_2} = W_{y_{21}} x_1 + W_{y_{22}} x_2 + b_{y_2} \\
\ I_{y_3} = W_{y_{31}} x_1 + W_{y_{32}} x_2 + b_{y_3}
\end{array}
\right. \\
\boldsymbol{y} &= (y_1, y_2, y_3) = \sigma_y( \boldsymbol{I_y} ) \tag{9} \\
\\
\boldsymbol{I_z} &= (I_{z_1}, I_{z_2}) = \boldsymbol{W_z} \boldsymbol{y} + \boldsymbol{b_z} \tag{10} \\
&\ \ \left|
\begin{array}{l}
\ I_{z_1} = W_{z_{11}} y_1 + W_{z_{12}} y_2 + W_{z_{13}} y_3 + b_{z_1} \\
\ I_{z_2} = W_{z_{21}} y_1 + W_{z_{22}} y_2 + W_{z_{23}} y_3 + b_{z_2}
\end{array}
\right. \\
\boldsymbol{z} &= (z_1, z_2) = \sigma_z( \boldsymbol{I_z} ) \tag{11}
\end{align}
$\text{(3)}$ は重みとバイアス、活性化関数を一気に適用したものでしたが、これから偏微分の式を考えていく関係で、途中に $\boldsymbol{I_y}$ と $\boldsymbol{I_z}$ を挟みました。等価な式であることはお分かりいただけると思います。
また、$\text{(7)}$ および $\text{(11)}$ において、入力層の次元は $x_1$ が $A$、$x_2$ が $B$ に対応し、出力層の次元は $z_1$ が $S$、$z_2$ が $C$ に対応するものとします。
損失関数 $L$ および活性化関数 $\sigma_y, \sigma_z$ はここでは あえて 定めず、最後に具体例として提示します。
出力層の重み・バイアスの偏微分
ではまず、損失関数に対する出力層の重み、バイアスの偏微分を求めていきます。
出力層から求めていく理由は、ニューラルネットワークの構造にあります。
重みやバイアスは自分の層と、自分よりも後ろの層の値に影響を与えるため、偏微分を考えるときは、重みやバイアスによるそれらの層の値の変化をすべて考慮しなければなりません。よって、後ろの層から進めていくほうが分かりやすいのです。
ここからは連鎖律も当たり前のように使っていきますので、$\text{(1)}$、$\text{(7)}$ ~ $\text{(11)}$ とにらめっこしながら、これからの式の導出をチェックしてみてください。
まずは $z_1$ のバイアスの偏微分から求めていきます。
\frac{\partial L}{\partial b_{z_1}} = \frac{\partial L}{\partial z_1} \cdot \frac{\partial z_1}{\partial I_{z_1}} \cdot \frac{\partial I_{z_1}}{\partial b_{z_1}} = \frac{\partial L}{\partial z_1} \cdot \sigma_z'(I_{z_1})\ \left( \because \frac{\partial I_{z_1}}{\partial b_{z_1}} = 1 \right) \tag{12}
損失関数の偏微分 ($\partial L/\partial z_1$) と活性化関数の偏微分 ($\partial z_1/\partial I_{z_1} = \sigma_z'(I_{z_1})$) が必要ですが、いまは両方とも明らかではありませんので、現時点でこれ以上は簡単にできません。
そしてここで、$\dfrac{\partial L}{\partial b_{z_1}} = \dfrac{\partial L}{\partial z_1} \cdot \dfrac{\partial z_1}{\partial I_{z_1}}$ であることを利用して、
\begin{align}
\frac{\partial L}{\partial W_{z_{11}}} &= \frac{\partial L}{\partial z_1} \cdot \frac{\partial z_1}{\partial I_{z_1}} \cdot \frac{\partial I_{z_1}}{\partial W_{z_{11}}} = \frac{\partial L}{\partial b_{z_1}} \cdot y_1 \tag{13} \\
\frac{\partial L}{\partial W_{z_{12}}} &= \frac{\partial L}{\partial z_1} \cdot \frac{\partial z_1}{\partial I_{z_1}} \cdot \frac{\partial I_{z_1}}{\partial W_{z_{12}}} = \frac{\partial L}{\partial b_{z_1}} \cdot y_2 \tag{14} \\
\frac{\partial L}{\partial W_{z_{13}}} &= \frac{\partial L}{\partial z_1} \cdot \frac{\partial z_1}{\partial I_{z_1}} \cdot \frac{\partial I_{z_1}}{\partial W_{z_{13}}} = \frac{\partial L}{\partial b_{z_1}} \cdot y_3 \tag{15}
\end{align}
と、バイアスの偏微分を使って重みの偏微分を表すことができます。$z_2$ のほうも同様で、
\frac{\partial L}{\partial b_{z_2}} = \frac{\partial L}{\partial z_2} \cdot \frac{\partial z_2}{\partial I_{z_2}} \cdot \frac{\partial I_{z_2}}{\partial b_{z_2}} = \frac{\partial L}{\partial z_2} \cdot \sigma_z'(I_{z_2})\ \left( \because \frac{\partial I_{z_2}}{\partial b_{z_2}} = 1 \right) \tag{16}
\begin{align}
\frac{\partial L}{\partial W_{z_{21}}} &= \frac{\partial L}{\partial z_2} \cdot \frac{\partial z_2}{\partial I_{z_2}} \cdot \frac{\partial I_{z_2}}{\partial W_{z_{21}}} = \frac{\partial L}{\partial b_{z_2}} \cdot y_1 \tag{17} \\
\frac{\partial L}{\partial W_{z_{22}}} &= \frac{\partial L}{\partial z_2} \cdot \frac{\partial z_2}{\partial I_{z_2}} \cdot \frac{\partial I_{z_2}}{\partial W_{z_{22}}} = \frac{\partial L}{\partial b_{z_2}} \cdot y_2 \tag{18} \\
\frac{\partial L}{\partial W_{z_{23}}} &= \frac{\partial L}{\partial z_2} \cdot \frac{\partial z_2}{\partial I_{z_2}} \cdot \frac{\partial I_{z_2}}{\partial W_{z_{23}}} = \frac{\partial L}{\partial b_{z_2}} \cdot y_3 \tag{19}
\end{align}
となります。
ここで、$\text{(12)}$ ~ $\text{(19)}$ を合わせて、各偏微分を行列 ($\partial L/\partial \boldsymbol{W_z}$) とベクトル ($\partial L/\partial \boldsymbol{b_z}$) で表すことを考えましょう。
その理由は 2 つあって、まず 1 つは、たくさんの式を簡潔にまとめられるからです。この例でも $\text{(12)}$ ~ $\text{(19)}$ で 8 つの式が必要ですが、行列とベクトルでうまくまとめられれば式は 2 つで済みます。
もう 1 つは、最急降下法の式 $\text{(2)}$ を見ると、
\boldsymbol{x}^{(k+1)} = \boldsymbol{x}^{(k)} - \eta \frac{\partial}{\partial\boldsymbol{x}^{(k)}} f(\boldsymbol{x}^{(k)}) \tag*{[2]}
となっていて、$\boldsymbol{W_z}$ や $\boldsymbol{b_z}$ と同じ形 (行列やベクトル) にしておいたほうが、線形代数学用のライブラリを使ったりできますので、計算がしやすいからです。
$\boldsymbol{W_z}$ はベクトルではなく行列じゃないか、と思うかもしれませんが、$\eta$ で定数倍して引き算をすることは、ベクトルだけでなく行列でも定義されている演算ですから問題ありません。
ではまずはバイアスの偏微分をベクトルの形に直します。
\frac{\partial L}{\partial \boldsymbol{b_z}} = \begin{bmatrix}
\dfrac{\partial L}{\partial b_{z_1}} \\
\dfrac{\partial L}{\partial b_{z_2}}
\end{bmatrix} = \begin{bmatrix}
\dfrac{\partial L}{\partial z_1} \cdot \sigma_z'(I_{z_1}) \\
\dfrac{\partial L}{\partial z_2} \cdot \sigma_z'(I_{z_2})
\end{bmatrix} = \frac{\partial L}{\partial \boldsymbol{z}} \circ \sigma_z'(\boldsymbol{I_z}) \tag{20}
ここで白いビュレット $\circ$ は「アダマール積 (Hadamard product)」を表し、成分ごとの積を意味します。
普通のビュレット $\cdot$ だとベクトルの内積と区別が付かないので、このような演算子を導入しています。
次に重みの偏微分を行列の形に直します。
\begin{align}
\frac{\partial L}{\partial \boldsymbol{W_z}} = \begin{bmatrix}
\dfrac{\partial L}{\partial W_{z_{11}}} & \dfrac{\partial L}{\partial W_{z_{12}}} & \dfrac{\partial L}{\partial W_{z_{13}}} \\
\dfrac{\partial L}{\partial W_{z_{21}}} & \dfrac{\partial L}{\partial W_{z_{22}}} & \dfrac{\partial L}{\partial W_{z_{23}}}
\end{bmatrix} &= \begin{bmatrix}
\dfrac{\partial L}{\partial b_{z_1}} \cdot y_1 & \dfrac{\partial L}{\partial b_{z_1}} \cdot y_2 & \dfrac{\partial L}{\partial b_{z_1}} \cdot y_3 \\
\dfrac{\partial L}{\partial b_{z_2}} \cdot y_1 & \dfrac{\partial L}{\partial b_{z_2}} \cdot y_2 & \dfrac{\partial L}{\partial b_{z_2}} \cdot y_3
\end{bmatrix} \\
&= \begin{bmatrix}
\dfrac{\partial L}{\partial b_{z_1}} \\
\dfrac{\partial L}{\partial b_{z_2}}
\end{bmatrix} \begin{bmatrix}
y_1 & y_2 & y_3
\end{bmatrix} \\
&= \frac{\partial L}{\partial \boldsymbol{b_z}} \cdot \boldsymbol{y}^{\top}
\end{align} \tag{21}
となります。偏微分の計算は結構ややこしかったですが、最終的に行列とベクトルの形にするとすごくスッキリした式にすることができました。
ちなみに、この $\text{(20)}$ と $\text{(21)}$ は隠れ層と出力層の次元数にかかわらず使えることを覚えておいてください。この 2 つの式の導出過程を見れば、次元が増えたり減ったりしても、同様に成り立つことがお分かりいただけると思います。
そういう面でも行列やベクトルの形式に直しておくと便利ですね。![]()
隠れ層の重み・バイアスの偏微分
次に、損失関数に対する隠れ層の重み、バイアスの偏微分を求めていきたいのですが、その前に、隠れ層の偏微分 ($\partial L/\partial \boldsymbol{y}$) を求めておきましょう。これは後で役に立ちます。
\frac{\partial L}{\partial y_1} = \frac{\partial L}{\partial z_1} \cdot \frac{\partial z_1}{\partial I_{z_1}} \cdot \frac{\partial I_{z_1}}{\partial y_1}\ ???
と、ここで困ったことが起きました。$\text{(10)}$ を見ると、$y_1$ は $I_{z_1}$ だけでなく $I_{z_2}$ を求める際にも使われているではありませんか!
でも心配はいりません。そう、我々には「連鎖律」がありますから、落ち着いて適用します。
\begin{align}
\frac{\partial L}{\partial y_1} &= \frac{\partial L}{\partial z_1} \cdot \frac{\partial z_1}{\partial I_{z_1}} \cdot \frac{\partial I_{z_1}}{\partial y_1} + \frac{\partial L}{\partial z_2} \cdot \frac{\partial z_2}{\partial I_{z_2}} \cdot \frac{\partial I_{z_2}}{\partial y_1} \\
&= \frac{\partial L}{\partial b_{z_1}} \cdot \frac{\partial I_{z_1}}{\partial y_1} + \frac{\partial L}{\partial b_{z_2}} \cdot \frac{\partial I_{z_2}}{\partial y_1} \\
&= \frac{\partial L}{\partial b_{z_1}} \cdot W_{z_{11}} + \frac{\partial L}{\partial b_{z_2}} \cdot W_{z_{21}}
\end{align} \tag{22}
これで OK です。
少し補足をすると、$y_1$ が $I_{z_1}$ と $I_{z_2}$ の両方の式に存在するということは、$y_1$ の値が変化すると、当然ですが $I_{z_1}$ と $I_{z_2}$ の両方の値の変化に影響を及ぼすことを意味しています。
$I_{z_1}$ と $I_{z_2}$ はどちらも損失関数 $L$ の値に影響するわけですから、偏微分を考える際には連鎖律を使わなければならないのです。
$y_2$ と $y_3$ の偏微分についても同様に求められます。
\begin{align}
\frac{\partial L}{\partial y_2} &= \frac{\partial L}{\partial z_1} \cdot \frac{\partial z_1}{\partial I_{z_1}} \cdot \frac{\partial I_{z_1}}{\partial y_2} + \frac{\partial L}{\partial z_2} \cdot \frac{\partial z_2}{\partial I_{z_2}} \cdot \frac{\partial I_{z_2}}{\partial y_2} \\
&= \frac{\partial L}{\partial b_{z_1}} \cdot \frac{\partial I_{z_1}}{\partial y_2} + \frac{\partial L}{\partial b_{z_2}} \cdot \frac{\partial I_{z_2}}{\partial y_2} \\
&= \frac{\partial L}{\partial b_{z_1}} \cdot W_{z_{12}} + \frac{\partial L}{\partial b_{z_2}} \cdot W_{z_{22}}
\end{align} \tag{23}
\begin{align}
\frac{\partial L}{\partial y_3} &= \frac{\partial L}{\partial z_1} \cdot \frac{\partial z_1}{\partial I_{z_1}} \cdot \frac{\partial I_{z_1}}{\partial y_3} + \frac{\partial L}{\partial z_2} \cdot \frac{\partial z_2}{\partial I_{z_2}} \cdot \frac{\partial I_{z_2}}{\partial y_3} \\
&= \frac{\partial L}{\partial b_{z_1}} \cdot \frac{\partial I_{z_1}}{\partial y_3} + \frac{\partial L}{\partial b_{z_2}} \cdot \frac{\partial I_{z_2}}{\partial y_3} \\
&= \frac{\partial L}{\partial b_{z_1}} \cdot W_{z_{13}} + \frac{\partial L}{\partial b_{z_2}} \cdot W_{z_{23}}
\end{align} \tag{24}
では $\text{(22)}$ ~ $\text{(24)}$ についても、まとめてベクトル ($\partial L/\partial \boldsymbol{y}$) で表しておきましょう。
\begin{align}
\frac{\partial L}{\partial \boldsymbol{y}} = \begin{bmatrix}
\dfrac{\partial L}{\partial y_1} \\
\dfrac{\partial L}{\partial y_2} \\
\dfrac{\partial L}{\partial y_3}
\end{bmatrix} &= \begin{bmatrix}
\dfrac{\partial L}{\partial b_{z_1}} \cdot W_{z_{11}} + \dfrac{\partial L}{\partial b_{z_2}} \cdot W_{z_{21}} \\
\dfrac{\partial L}{\partial b_{z_1}} \cdot W_{z_{12}} + \dfrac{\partial L}{\partial b_{z_2}} \cdot W_{z_{22}} \\
\dfrac{\partial L}{\partial b_{z_1}} \cdot W_{z_{13}} + \dfrac{\partial L}{\partial b_{z_2}} \cdot W_{z_{23}}
\end{bmatrix} \\
&= \begin{bmatrix}
W_{z_{11}} & W_{z_{21}} \\
W_{z_{12}} & W_{z_{22}} \\
W_{z_{13}} & W_{z_{23}}
\end{bmatrix} \begin{bmatrix}
\dfrac{\partial L}{\partial b_{z_1}} \\
\dfrac{\partial L}{\partial b_{z_2}}
\end{bmatrix} \\
&= \boldsymbol{W_z}^{\top} \cdot \frac{\partial L}{\partial \boldsymbol{b_z}}
\end{align} \tag{25}
途中、行列演算を考慮する関係で重みとバイアスの順番が入れ替わっているので、少々見づらいかもしれませんが、地道に計算していくとこのようになります。
そして $\text{(25)}$ も、$\text{(20)}$ や $\text{(21)}$ と同じように、行列とベクトルで表現したことによって、隠れ層と出力層の次元数にかかわらず使える式になっています。
なお、$\text{(25)}$ は重み行列を転置していますが、いざプログラミングしようとすると、大規模なネットワークでは転置に時間がかかるかもしれません。
そうならないよう工夫がされている線形代数学用のライブラリもありますが、もし素直に転置するときは、以下 $\text{(26)}$ が成り立つことを利用して、重み行列を転置せずそのまま使うようにするとよいでしょう。
\boldsymbol{W_z}^{\top} \cdot \frac{\partial L}{\partial \boldsymbol{b_z}} = \left( \dfrac{\partial L}{\partial \boldsymbol{b_z}}^{\top} \cdot \boldsymbol{W_z} \right)^{\top} \tag{26}
ここまで来れば、隠れ層の重みとバイアスの偏微分を求めるのは簡単です。
損失関数に対する隠れ層の偏微分 ($\partial L/\partial \boldsymbol{y}$) が求められていますし、$\text{(3)}$ や $\text{(8)}$ ~ $\text{(11)}$ を見ると、ニューラルネットワークの計算式は隠れ層も出力層も変わらないわけですから、$\text{(20)}$ と $\text{(21)}$ の記号を変えて再利用ができます。
\begin{align}
\frac{\partial L}{\partial \boldsymbol{b_y}} &= \frac{\partial L}{\partial \boldsymbol{y}} \circ \sigma_y'(\boldsymbol{I_y}) \tag{27}\\
\frac{\partial L}{\partial \boldsymbol{W_y}} &= \frac{\partial L}{\partial \boldsymbol{b_y}} \cdot \boldsymbol{x}^{\top} = \left( \frac{\partial L}{\partial \boldsymbol{y}} \circ \sigma_y'(\boldsymbol{I_y}) \right) \cdot \boldsymbol{x}^{\top} \tag{28}
\end{align}
あまりにも呆気なくて、嘘くさく感じるかもしれませんが、これで合ってます。
それでも不安に感じたら、検算をして $\partial L / \partial b_{y_1}$ から順に求めていくとよいでしょう。8 前節の $\text{(12)}$ ~ $\text{(21)}$ と同じような計算経過をたどって、$\text{(27)}$ と $\text{(28)}$ を導くことができます。
あ、入力層の偏微分 ($\partial L / \partial \boldsymbol{x}$) を求める必要はありません。入力層に重みやバイアスはありませんから、求めても使いどころがないためです。
損失関数と活性化関数
ここで、最後まで決めていなかったものについて手を付けることにしましょう。そう、損失関数 と 活性化関数 です。
最初に、この 2 つは あえて 最後に提示すると書きました。
損失関数と活性化関数を事前に決定してしまうと、式を計算していく過程で、分母と分子に同じ項ができて消えてしまったり、式の前後に一部の項が移動してしまったりして、その損失関数、その活性化関数でしか通用しない式になりがちです。
その状態で覚えてしまうと、損失関数、活性化関数を変更したいときに応用が利きませんので、最後に考えることにしました。
損失関数は 2 次損失を使ってみましょう。ただし、係数 $1/2$ を追加します。
L = \frac{1}{2} \{(z_1 - T_1)^2 + (z_2 - T_2)^2\}
わざわざ $1/2$ を付ける理由は、偏微分をしてみると分かります。
\begin{align}
\frac{\partial L}{\partial z_1} &= \frac{1}{2} \cdot 2(z_1 - T_1) \cdot 1 = z_1 - T_1 \\
\frac{\partial L}{\partial z_2} &= \frac{1}{2} \cdot 2(z_2 - T_2) \cdot 1 = z_2 - T_2 \\
\frac{\partial L}{\partial \boldsymbol{z}} &= \begin{bmatrix}
\dfrac{\partial L}{\partial z_1} \\
\dfrac{\partial L}{\partial z_2}
\end{bmatrix} = \begin{bmatrix}
z_1 - T_1 \\
z_2 - T_2
\end{bmatrix} = \boldsymbol{z} - \boldsymbol{T} \tag{29}
\end{align}
係数 $1/2$ が付いていても損失関数の大小関係は崩れませんから問題ありませんし、偏微分の際に肩の 2 乗が降りてくるのを係数で相殺できるため、式を簡単にすることができます。
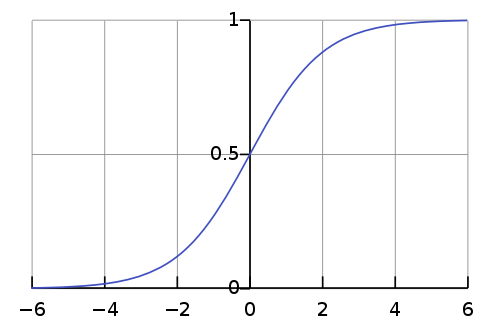
次に活性化関数ですが、今回は隠れ層、出力層とも「標準シグモイド関数 (standard sigmoid function)」を使ってみます。9
シグモイド関数は非線形の関数で、関数 $\sigma(x)$ およびその導関数 $\sigma'(x)$ は以下のとおりです。
\begin{align}
\sigma(x) &= \frac{1}{1 + e^{-x}} \\
\\
\sigma'(x) &= \left( \frac{1}{1 + e^{-x}} \right)' = \{ (1 + e^{-x})^{-1} \}' \\
&= -1 \cdot (1 + e^{-x})^{-2} \cdot e^{-x} \cdot (-1) \\
&= \frac{e^{-x}}{(1 + e^{-x})^2} = \frac{1 + e^{-x}}{(1 + e^{-x})^2} - \frac{1}{(1 + e^{-x})^2} \\
&= \frac{1}{1 + e^{-x}} - \left(\frac{1}{1 + e^{-x}}\right)^2 = \sigma(x) - \{\sigma(x)\}^2 \\
&= \sigma(x) \{ 1 - \sigma(x) \} \tag{30}
\end{align}
この関数を活性化関数に使うメリットとして、
- 定義域 $(-\infty, \infty)$ に対して値域 $(0, 1)$ であり、今回の半加算器の出力範囲として適当である。
- $\text{(30)}$ で表すとおり、1 階導関数を自分自身を使って表すことができる。
があります。$\text{(30)}$ を用いて隠れ層と出力層の活性化関数の微分 $\sigma_y'( \boldsymbol{I_y} ), \sigma_z'( \boldsymbol{I_z} )$ を求めると、
\begin{align}
\sigma_y'( \boldsymbol{I_y} ) &= \begin{bmatrix}
\sigma_y'( I_{y_1} ) \\
\sigma_y'( I_{y_2} ) \\
\sigma_y'( I_{y_3} )
\end{bmatrix} = \begin{bmatrix}
\sigma_y( I_{y_1} ) \{ 1 - \sigma_y( I_{y_1} ) \} \\
\sigma_y( I_{y_2} ) \{ 1 - \sigma_y( I_{y_2} ) \} \\
\sigma_y( I_{y_3} ) \{ 1 - \sigma_y( I_{y_3} ) \}
\end{bmatrix} = \begin{bmatrix}
y_1 ( 1 - y_1 ) \\
y_2 ( 1 - y_2 ) \\
y_3 ( 1 - y_3 )
\end{bmatrix} \\
&= \boldsymbol{y} \circ (\boldsymbol{1} - \boldsymbol{y}) \tag{31}
\end{align}
\begin{align}
\sigma_z'( \boldsymbol{I_z} ) &= \begin{bmatrix}
\sigma_z'( I_{z_1} ) \\
\sigma_z'( I_{z_2} )
\end{bmatrix} = \begin{bmatrix}
\sigma_z( I_{z_1} ) \{ 1 - \sigma_z( I_{z_1} ) \} \\
\sigma_z( I_{z_2} ) \{ 1 - \sigma_z( I_{z_2} ) \}
\end{bmatrix} = \begin{bmatrix}
z_1 ( 1 - z_1 ) \\
z_2 ( 1 - z_2 )
\end{bmatrix} \\
&= \boldsymbol{z} \circ (\boldsymbol{1} - \boldsymbol{z}) \tag{32}
\end{align}
となり、なるほど、とても簡単になりました (アダマール積になることに注意)。
式 $\text{(29)}$、$\text{(31)}$、$\text{(32)}$ を踏まえて、損失関数に対する重みとバイアスの偏微分の最終的な式は、
\begin{align}
\frac{\partial L}{\partial \boldsymbol{b_z}} &= \frac{\partial L}{\partial \boldsymbol{z}} \circ \sigma_z^{\prime}(\boldsymbol{I_z}) = (\boldsymbol{z} - \boldsymbol{T}) \circ \boldsymbol{z} \circ (\boldsymbol{1} - \boldsymbol{z}) \\
\frac{\partial L}{\partial \boldsymbol{W_z}} &= \frac{\partial L}{\partial \boldsymbol{b_z}} \cdot \boldsymbol{y}^{\top} \tag*{[21]} \\
\frac{\partial L}{\partial \boldsymbol{y}} &= \boldsymbol{W_z}^{\top} \cdot \frac{\partial L}{\partial \boldsymbol{b_z}} \tag*{[25]} \\
\frac{\partial L}{\partial \boldsymbol{b_y}} &= \frac{\partial L}{\partial \boldsymbol{y}} \circ \sigma_y^{\prime}(\boldsymbol{I_y}) = \frac{\partial L}{\partial \boldsymbol{y}} \circ \boldsymbol{y} \circ (\boldsymbol{1} - \boldsymbol{y}) \\
\frac{\partial L}{\partial \boldsymbol{W_y}} &= \frac{\partial L}{\partial \boldsymbol{b_y}} \cdot \boldsymbol{x}^{\top} \tag*{[28]}
\end{align}
となります。ようやくこれですべて揃いました。あとはひたすらコンピュータに計算させるだけです。
学習させよう
ニューラルネットワークの学習は、おおむね以下の手順で行います。場合によってはこのとおりの手順にならないことがありますので、参考程度に見てください。
- 重みとバイアスを初期化する。
- 以下を学習回数ぶん繰り返す。
- 以下を入力のぶん繰り返す。
- 現在の重みとバイアスを使い、入力データから各層の値を計算する (順伝播)。
- 損失関数を計算する。偏微分の計算に直接必要ではないが、学習の経過を確認できる。
- 損失関数に対する各層の重みとバイアスの偏微分を計算する。
- 入力ごとの損失関数に対する偏微分 ($\partial L/\partial w$) から、全体損失関数に対する偏微分 ($\partial L^{(all)}/\partial w$) を計算する。
- 最急降下法を使い、重みとバイアスを修正する。
- 以下を入力のぶん繰り返す。
「初期化」についてここまで言及してきませんでしたが、1 つ注意点を挙げておくと、重みとバイアスの初期化は 乱数を使うのが基本 であり、決して 同じ値で初期化してはいけない ということです。
同じ値で初期化してしまうと、損失関数に対する偏微分 ($\partial L/\partial w$) がすべてのノードで等しくなり、最急降下法による修正量も同じになるため、ノードにかかわらず重み、バイアスが常に同じ値になります。
同じ重み、バイアスを持つノードは 1 つにまとめることができますので、その層の次元数が小さくなってしまいます。これはすなわち、表現力が低下した ことを意味するのです。
実際、この状態ではニューラルネットワークの学習は、多くの場合うまくいきません。
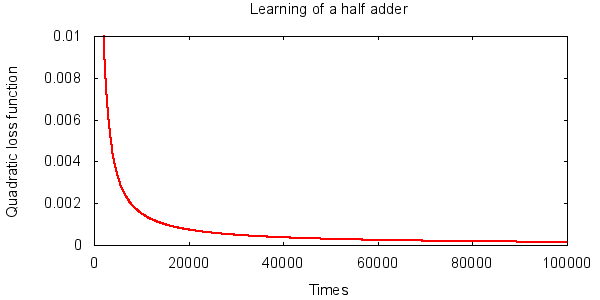
以上に注意しつつ、半加算器のニューラルネットワークを学習させたところ、今回 10 は以下の結果になりました。
set term png size 600,300 transparent font 'Arial' 11
set output 'half_adder.png'
set title 'Learning of a half adder'
set xlabel 'Times'
set ylabel 'Quadratic loss function'
unset key
set lmargin 10.5
set rmargin 3.5
set tmargin 2
set bmargin 3
set xrange [0:100000]
set yrange [0:0.01]
plot 'half_adder.csv' with lines linewidth 2
学習回数が増えるにしたがい、損失関数が順調に小さくなっていくのが分かります。うまく学習できているようです。
今回は重み、バイアスの初期化には閉区間 $[-8, 8]$ の一様分布乱数を使い、学習率 (最急降下法の係数 $\eta$) は 0.3 としました。
ソースコードは Gist に投稿していますので、ご興味があれば、隠れ層の次元数や乱数分布、学習率の違いによる、学習結果の違いを比較してみてください。11
誤差逆伝播法
前章は、誤差逆伝播法とは何なのかという点をすっ飛ばして、勢いに任せて実例を長々と書いてしまいました。ここでは誤差逆伝播法についてまとめていきます。
順伝播と逆伝播
まず、半加算器の学習に出てきた数式の一部をまとめます。
\begin{align}
\boldsymbol{x} &= (x_1, x_2) \tag*{[7]} \\
\boldsymbol{y} &= \sigma_y( \boldsymbol{W_y} \boldsymbol{x} + \boldsymbol{b_y} ) \tag{9'} \\
\boldsymbol{z} &= \sigma_z( \boldsymbol{W_z} \boldsymbol{y} + \boldsymbol{b_z} ) \tag{11'}\\
\\
\frac{\partial L}{\partial \boldsymbol{z}} &= \boldsymbol{z} - \boldsymbol{T} \tag*{[29]} \\
\frac{\partial L}{\partial \boldsymbol{b_z}} &= \frac{\partial L}{\partial \boldsymbol{z}} \circ \sigma_z'( \boldsymbol{W_z} \boldsymbol{y} + \boldsymbol{b_z} ) \tag{20'} \\
\frac{\partial L}{\partial \boldsymbol{W_z}} &= \frac{\partial L}{\partial \boldsymbol{b_z}} \cdot \boldsymbol{y}^{\top} \tag*{[21]} \\
\frac{\partial L}{\partial \boldsymbol{y}} &= \boldsymbol{W_z}^{\top} \cdot \frac{\partial L}{\partial \boldsymbol{b_z}} \tag*{[25]} \\
\frac{\partial L}{\partial \boldsymbol{b_y}} &= \frac{\partial L}{\partial \boldsymbol{y}} \circ \sigma_y'( \boldsymbol{W_y} \boldsymbol{x} + \boldsymbol{b_y} ) \tag{27'} \\
\frac{\partial L}{\partial \boldsymbol{W_y}} &= \frac{\partial L}{\partial \boldsymbol{b_y}} \cdot \boldsymbol{x}^{\top} \tag*{[28]}
\end{align}
$\text{(7)}$、$\text{(9')}$、$\text{(11')}$ を見ると、層の値を求めるためには、前の層の値が必要になることが分かると思います。
そして、$\text{(29)}$、$\text{(20')}$、$\text{(21)}$、$\text{(25)}$、$\text{(27')}$、$\text{(28)}$ を見ると、偏微分を求めるためには、後ろの層の偏微分が必要になることが分かります。
層の値を入力層から出力層に向かって順番に計算していく過程を「順伝播」と説明しましたが、それに対して、偏微分を出力層から入力層に向かって順番に計算していく過程を「逆伝播 (backward propagation)」といいます。
そして、損失関数 $L$ を 誤差 と見立てて、逆伝播によって重みとバイアスを修正していくアルゴリズムが「誤差逆伝播法」なのです。
前章で、誤差逆伝播法が具体的に何を示しているのか明らかにせずにニューラルネットワークの学習を進めましたが、何のことはなく、やっていたことは誤差逆伝播法そのものです。
一般化
ここでニューラルネットワークの計算モデルについておさらいしておきましょう。
\boldsymbol{l}^{(k+1)} = \sigma^{(k+1)}(\boldsymbol{W}^{(k+1)} \boldsymbol{l}^{(k)} + \boldsymbol{b}^{(k+1)}) \tag*{[3]}
この記号に合わせて、誤差逆伝播法の式も示していきます。
\begin{align}
\frac{\partial L}{\partial \boldsymbol{l}^{(k)}} &= \left\{ \begin{array}{ll}
\text{Depend on } L & (\text{if the } k \text{-th layer is the output one}) \\
{\boldsymbol{W}^{(k+1)}}^{\top} \cdot \dfrac{\partial L}{\partial \boldsymbol{b}^{(k+1)}} & (\text{otherwise})
\end{array} \right. \tag{33} \\
\frac{\partial L}{\partial \boldsymbol{b}^{(k)}} &= \frac{\partial L}{\partial \boldsymbol{l}^{(k)}} \circ \sigma'^{(k)}( \boldsymbol{W}^{(k)} \boldsymbol{l}^{(k-1)} + \boldsymbol{b}^{(k)} ) \tag{34} \\
\frac{\partial L}{\partial \boldsymbol{W}^{(k)}} &= \frac{\partial L}{\partial \boldsymbol{b}^{(k)}} \cdot {\boldsymbol{l}^{(k-1)}}^{\top} \tag{35}
\end{align}
層の番号 $k$ を出力層から入力層に向かって順番に減らしていき、損失関数に対する各層の重みとバイアスの偏微分を求めていきます。
ここで注意するべきことは、$k$ 番目の層が出力層だと損失関数次第で式が変わるため、$\partial L/\partial \boldsymbol{l}^{(k)}$ に場合分けが発生することです。
一般化した式 $\text{(33)}$ ~ $\text{(35)}$ は記号を変えただけなのですが、半加算器の実例からすると、かえって分かりにくくなってしまっている気がします。
正直なところ、一般化した式で覚えるよりも、実例での式 $\text{(29)}$、$\text{(20')}$、$\text{(21)}$、$\text{(25)}$、$\text{(27')}$、$\text{(28)}$ で覚えておいたほうが楽かなと思います。
あわせて読みたい
- ニューラルネットワークと深層学習
- 誤差逆伝播法のノート by @Ugo-Nama
- Denoising Autoencodersにおける確率的勾配降下法(数式の導出)
- TSG Machine Learning » #08 確率的勾配降下法
おわりに
記事が短いと詳細な説明ができず分かりにくくなってしまうし、長いとそもそも読む気が起こらない、というジレンマに陥った結果、この記事では長くなるほうを取りました。しかしそれによって分かりやすくなったかは不明ですが…。
短すぎず長すぎずちょうどよくまとめられる方が羨ましいと思う今日この頃です。
誤差逆伝播法は、簡単なメモ書きくらいの分量のものから、それこそ本が書けてしまいそうな分量のものまで、たくさんの解説が存在するのですが、自分自身が理解するためには、結局のところ自分自身で数式をこねくり回し、自分自身でプログラミングしてみて、そのときの気付きを頭にたたき込むことが一番の方法ではないかと思います。
冒頭で書いたように、この記事は私が「誤差逆伝播法」を勉強するうえで必要だった情報を記録したものですが、この記事が皆さまのお役に立てたら嬉しいです。
もし数式や考え方などでご不明な点があれば、ご遠慮なくコメントしてくださいませ。
最後までお読みいただきありがとうございました。
奥付
記事には自分なりにしっかりと目を通してはいますが、誤字脱字、番号参照の間違い、表現の誤りなどがありましたら、コメント欄にてご指摘くださると幸いです。
- 初稿 「誤差逆伝播法をはじめからていねいに」
- 2016/09/06
-
「連鎖律」については英語版 Wikipedia のほうがより詳細に記載されています。 ↩
-
画像は A Neural Network in 13 lines of Python (Part 2 - Gradient Descent) より引用しました。 ↩
-
活性化関数が線形である多層ニューラルネットワークには、それと等価な単層 (つまり入力層と出力層だけ) のニューラルネットワークが存在することが分かっています。ニューラルネットワークは表現力を強化するために多層構造にされるため、線形関数を活性化関数に採用するとその意味が失われてしまいます。 ↩
-
正確にいうと、このノルムは「ユークリッドノルム (Euclidean norm)」あるいは「2-ノルム」などとよばれます。 ↩
-
依存するパラメータが少ないこと。スパース性を高めると、過学習 (overfitting) (あるいは過剰適合とも) を防ぐことができ、より安定した (よく「剛健である」とか「ロバストネスが高い」といわれる) ネットワークになります。 ↩
-
この記事ではこれ以降「全体損失関数」という名称をたびたび使いますが、一般的な用語ではありませんのでご注意ください。 ↩
-
ちなみに、排他的論理和は隠れ層のない 2 層のニューラルネットワークでは表現できないことが分かっています。 ↩
-
自分も「本当かなぁ?」と不思議に思って検算しました。これに限った話ではありませんが、自分の手でノートに計算式を書いて解いていくと、理論が頭の中にすっと入ってくるのが実感できます。実際に解いてみることは非常に大事です…ということを注釈でさらっと書いてみる。 ↩
-
画像は Sigmoid function (Wikipedia 英語版) より引用しました。 ↩
-
ニューラルネットワークの学習は、損失関数や学習率 (最急降下法の偏微分項に付く係数)、重みとバイアスの初期値等、たくさんのパラメータがあるため、その値によっては学習がうまくいくときといかないときがあります。 ↩
-
ソースコードはとにかく分かりやすさを重視して、速度や効率は一切気にしていません。そこについてはご勘弁くださいませ。 ↩