概要
Unity以外でもそうですが、メッシュは頂点の塊です。
そしてそれらはTriangleやそれらを結ぶIndexで構成されています。
つまり、勝手に順番を変えてしまうと頂点の情報はぐちゃぐちゃになってしまい、ちゃんとしたオブジェクトとして表示することはできません。
そのため、メッシュを切断して別のオブジェクトに分けようとすると、それなりに頂点郡を計算してポリゴンを縫い合わせてやる必要があります。
今回はそんなメッシュのカットを行うサンプルを公開してくれている人がいたので、そのサンプルを読んだメモを書いていきます。
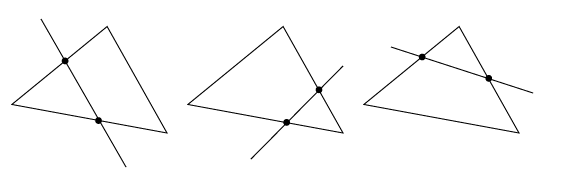
左側の3本のラインがカット面を示していて、その平面できれいに切断されているのが分かるかと思います。
しかも、しっかりと切断面に別のマテリアルが割り当てられているのにも注目です。
大まかな流れ
まずは大まかな流れから説明します。
具体的になにをしているかを見るよりも、切断に必要な処理がなんなのか、という視点で見てもらうといいかと思います。
全体像を把握した上でコードを読んでいくと処理内容が推測しやすくなり、理解を促すはずです。
- 切断する平面を定義する
- 切断するオブジェクトを選択する
- 選択されたメッシュの全頂点に対し、平面の左側か右側かを計算する
※ 評価する単位はポリゴン(トライアングル)単位で行う - (3)の際、3頂点すべてが平面の左か右のどちらかに寄っている場合は切断対象外なので、左側か右側かだけを判別して適切に頂点を保持する
※ 最終的にふたつのオブジェクトに分割するため、左右の頂点情報などを保持するオブジェクトを用意してそれに格納する - (3)の際、3頂点が平面の左右にバラけた場合に切断処理を実行する
- 切断処理はまず、3頂点がそれぞれ平面の左右どちらにあるかを判断し、(3)同様に適切に振り分ける
- その後、切断平面と重なる2頂点を新しい頂点として計算する(※1)
- すべての頂点に対して振り分けおよび頂点の生成が終わったら、(7)で生成した新頂点すべてに対しペアを算出しポリゴンを形成する
- 最後に、生成したポリゴンを用いて切断面を定義し、新しいマテリアルを適用する
※1 ... 三角形(ポリゴン)を線(平面)で分断するとどこをどう切っても必ず2辺と交わる。つまり新しい頂点は2つ作られる。
実装と考え方
頂点が平面のどちら側にあるかを調べる
頂点が平面のどちら側にあるかは内積を使って簡単に調べることができます。
具体的には、点 $p$ と、平面の位置 $p_0$、および面の法線 $n$ を使って、
(p - p_0) \cdot n < 0 ... 裏 \\
(p - p_0) \cdot n > 0 ... 表 \\
(p - p_0) \cdot n = 0 ... 平面上
として計算することができます。
ちなみに UnityEngine.Plane クラスにはこうした平面に対する処理を簡単にしてくれるメソッドが多数あるので、実際はそちらを利用したほうが手軽です。
サンプルのコードを抜粋すると以下になります。
sides[0] = blade.GetSide(victim_mesh.vertices[p1]);
sides[1] = blade.GetSide(victim_mesh.vertices[p2]);
sides[2] = blade.GetSide(victim_mesh.vertices[p3]);
これは、切断対象となったメッシュの、計算中の頂点が平面のどちらにあるかを bool で取得している部分です。
平面に分断された点を求める
さて、上記の平面の表裏の判定により、大部分の頂点は左右に適切に振り分けることができます。
残るは、平面と交差しているポリゴンの各辺を分離して、新しい頂点を得ることができれば、ひとまずすべての頂点を左右に振り分け、かつ切断面に使える頂点郡を得ることができます。
ということで、辺を分断する頂点の求め方です。
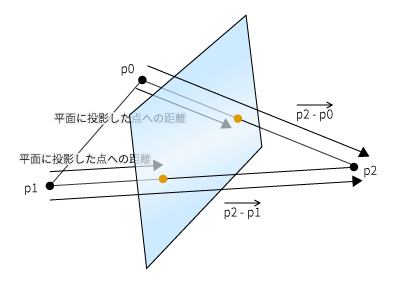
色々文章で説明する前に、下の図を見てもらうと分かりやすいかと思います。
グラデーションがかかっている平面が切断面です。
この平面により、頂点が左右どちらかに分断されます。
図では $p_0$ と $p_1$ が平面の左側、$p_2$ が平面の右側、そして黄色い点が分断された頂点になります。
平面方向への距離を算出する
点の割り出し方は、$p_0$ および $p_1$ から、$p_2$ 方向への距離を算出します。($\vec{p_2 p_0}$ と $\vec{p_2 p_1}$)
(平面への距離の算出は、以前書いた「[Unity] 任意の無限遠の平面とベクトルとの交点を求める」を見てもらうと分かるかと思います)
が、上の方でも書きましたが、UnityEngine.Plane クラスにはこの距離を算出するのに適したメソッドがあります。
参考にしたコードでもそれを利用して計算を行っています。
その部分だけを抜粋すると、
blade.Raycast(new Ray(leftPoints[0], (rightPoints[0] - leftPoints[0]).normalized), out distance);
ここで blade は切断面を表す UnityEngine.Plane クラスのインスタンスです。
これに Raycast メソッドがあり、レイを飛ばしてやることで、任意の点と方向を元に、平面への距離を算出することができます。
(上の例では out distance に距離が入り、メソッド自体は、平面とレイが交差する場合に true を返します)
辺と距離から切断頂点を求める
Raycast を用いて切断頂点までの「距離」を求めることができました。
ただこれはスカラー値で、あくまで「距離」しか分かりません。
しかし、辺の長さとの比率と各頂点情報から平面上の頂点(つまり分断点)を求めることができます。
具体的には
- 辺の長さを計算する
- 「頂点までの距離 / 辺の長さ」= 比率
- 辺の両端の点の間を(2)の比率で補完する
この3工程を行うことで頂点を求めることができます。
これを、分断された辺の分、つまり2辺分行うことで分断された頂点を求めることができる、というわけです。
サンプルコードの該当部分を抜粋すると以下のような形になります。
// ---------------------------
// 左側の処理
// 定義した面と交差する点を探す。
// つまり、平面によって分割される点を探す。
// 左の点を起点に、右の点に向けたレイを飛ばし、その分割点を探る。
blade.Raycast(new Ray(leftPoints[0], (rightPoints[0] - leftPoints[0]).normalized), out distance);
// 見つかった交差点を、頂点間の距離で割ることで、分割点の左右の割合を算出する
normalizedDistance = distance / (rightPoints[0] - leftPoints[0]).magnitude;
// カット後の新頂点に対する処理。フラグメントシェーダでの補完と同じく、分割した位置に応じて適切に補完した値を設定する
Vector3 newVertex1 = Vector3.Lerp(leftPoints[0], rightPoints[0], normalizedDistance);
Vector2 newUv1 = Vector2.Lerp(leftUvs[0], rightUvs[0], normalizedDistance);
Vector3 newNormal1 = Vector3.Lerp(leftNormals[0] , rightNormals[0], normalizedDistance);
// 新頂点郡に新しい頂点を追加
new_vertices.Add(newVertex1);
↑の日本語は解説用に自分が付け加えたコメントです。
切断面を構築する
上記までで全頂点の振り分け、および新頂点の算出が終わりました。
最後は、新しく生成された頂点を利用して、切断面のポリゴンを形成します。
新頂点のペアを選択し、ポリゴンを形成する
切断面の形成には、上記で算出した新頂点を使って行います。
基本的な考え方は以下のフローになります。
- 生成された頂点郡からペアとなる頂点を探し、それを順番に配列に格納する(※1)
- 新頂点のペアの探索が終わった段階でペアごとの順番に配列が形成されている
- (1)の配列の重心を計算する(単純に全頂点足して、頂点数で割る)
- (3)で算出した重心と、配列の頂点を使ってポリゴンを形成する
- (4)のポリゴンを、左右のメッシュそれぞれに追加する
- その際、左右でポリゴンの法線を逆向きにする(※2)
※1 ... 切断対象となったポリゴンから必ず2頂点が生成される
※2 ... 切断面は左右のオブジェクトそれぞれに必要で、単純に向きが逆のため
該当のコードを示すと以下になります。
/// <summary>
/// カットを実行
/// </summary>
static void Capping()
{
// カット用頂点追跡リスト
// 具体的には新頂点全部に対する調査を行う。その過程で調査済みをマークする目的で利用する。
capVertTracker.Clear();
// 新しく生成した頂点分だけループする=全新頂点に対してポリゴンを形成するため調査を行う
// 具体的には、カット面を構成するポリゴンを形成するため、カット時に重複した頂点を網羅して「面」を形成する頂点を調査する
for (int i = 0; i < new_vertices.Count; i++)
{
// 対象頂点がすでに調査済みのマークされて(追跡配列に含まれて)いたらスキップ
if (capVertTracker.Contains(new_vertices[i]))
{
continue;
}
// カット用ポリゴン配列をクリア
capVertpolygon.Clear();
// 調査頂点と次の頂点をポリゴン配列に保持する
capVertpolygon.Add(new_vertices[i + 0]);
capVertpolygon.Add(new_vertices[i + 1]);
// 追跡配列に自身と次の頂点を追加する(調査済みのマークをつける)
capVertTracker.Add(new_vertices[i + 0]);
capVertTracker.Add(new_vertices[i + 1]);
// 重複頂点がなくなるまでループし調査する
bool isDone = false;
while (!isDone)
{
isDone = true;
// 新頂点郡をループし、「面」を構成する要因となる頂点をすべて抽出する。抽出が終わるまでループを繰り返す
// 2頂点ごとに調査を行うため、ループは2単位ですすめる
for (int k = 0; k < new_vertices.Count; k += 2)
{ // go through the pairs
// ペアとなる頂点を探す
// ここでのペアとは、いちトライアングルから生成される新頂点のペア。
// トライアングルからは必ず2頂点が生成されるため、それを探す。
// また、全ポリゴンに対して分割点を生成しているため、ほぼ必ず、まったく同じ位置に存在する、別トライアングルの分割頂点が存在するはずである。
if (new_vertices[k] == capVertpolygon[capVertpolygon.Count - 1] && !capVertTracker.Contains(new_vertices[k + 1]))
{ // if so add the other
// ペアの頂点が見つかったらそれをポリゴン配列に追加し、
// 調査済マークをつけて、次のループ処理に回す
isDone = false;
capVertpolygon.Add(new_vertices[k + 1]);
capVertTracker.Add(new_vertices[k + 1]);
}
else if (new_vertices[k + 1] == capVertpolygon[capVertpolygon.Count - 1] && !capVertTracker.Contains(new_vertices[k]))
{ // if so add the other
isDone = false;
capVertpolygon.Add(new_vertices[k]);
capVertTracker.Add(new_vertices[k]);
}
}
}
// 見つかった頂点郡を元に、ポリゴンを形成する
FillCap(capVertpolygon);
}
}
上記のコードを理解する上で地味にポイントだったのは、重複する頂点が存在する、という点。
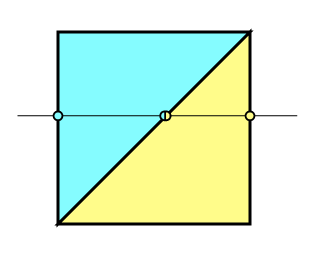
簡単のためにまず板ポリを考えてみます。
すると、板ポリは2枚のポリゴンで形成されますが、これを切断すると新頂点は4つ生成されます。
三角形(ポリゴン)1枚に対して2頂点生成されるからですね。
そして重複する点は1つです。
上記画像の左右の頂点はそれぞれの色に対応したポリゴンから生成された頂点です。
そして中央のものが2つの色に分けられていますが、これが重複した頂点になります。
左右それぞれのポリゴンから頂点が生成されるので4つ生成されているのが分かるかと思います。
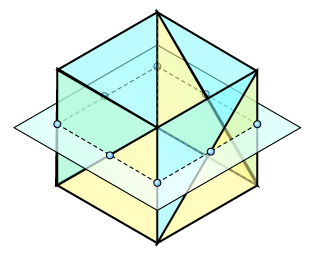
さて、今度はこれをキューブに拡張して考えると、先程は重複しなかった両端の点も、キューブの側面側の頂点と重複することになります。
結果としてすべての新頂点が必ず2つずつ重なることになります。
なので冒頭の動画のように、キューブを切断すると新頂点は16個生成され、実際に切断面のポリゴンとして利用される頂点は8つになります。
実際に、上図の点を数えると8個あるのが分かるかと思います。それぞれが重複しているため、新頂点として生成されるのは16、ということですね。
カット面をグルーピングする
上記のfor文の入れ子になっている方(k += 2で回している方)は、ここで生成された重複頂点を調べてグルーピングする役割を担っています。
すでに説明したように、Cubeを切断した場合、Cubeをぐるっと取り囲むように16個の頂点が作られます。
対象がCubeひとつならこの頂点郡をひとつのカット面として利用しても問題ありませんが、大体の場合はモデルは複雑な形状をしています。
例えば角を持つモンスターが腕を振り上げているシーンを想像してください。
そしてその振り上げた手と角を一度に切断した場合、角の部分と腕の部分、それぞれ「ふたつのカット面」が生成されるのがイメージできるかと思います。
この「角」と「腕」のカット面を形成する頂点郡をグルーピングするのが前述のグルーピングの役割、と書いた意味です。
実装としてはシンプルです。
上記では「角」と「腕」を例に出しました。
そして大体の場合において、このふたつのカット平面の頂点は重なることがありません。
つまり、入れ子のfor文が行っているのは、必ず重複頂点が生成される事実を利用して、重複頂点を結んでいくことで「角」と「腕」のカット面を意味的にふたつにグルーピングしている、というわけです。
上の板ポリの例で言えば、最初に青い色の頂点をグループに追加し、そこから調査を開始します。(調査用のリストとしてcapVertTrackerを利用しています)
最後に追加した頂点と同じ位置にある頂点を探します。
すると、重複した位置にある黄色い頂点が見つかります。
そして「見つかった頂点の次の頂点」をcapVertTrackerリストに加え、再度検索を行います。(板ポリの例で言えば右端の黄色い頂点)
板ポリではこれでグルーピングが完了します。
仮に、板ポリの次に示したCubeの例で言えば連続的に別の面の頂点が見つかります。
あとは同じ検索・追加処理を、対象頂点が見つからなくなるまで繰り返すことで、無事にカット面を形成する頂点郡のグルーピングが完成する、というわけです。
新頂点を結び、ポリゴンを形成する
さぁ、これで必要な情報はすべて整いました。
あとは調べられた頂点を使ってポリゴンを形成する、つまり3頂点を選び出してそれを結んでいく作業です。
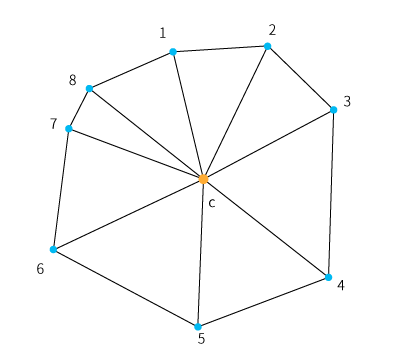
ただ、上図とコードを見てもらうと分かりますが、新しく生成された頂点は16、うちポリゴン形成に利用するのは8頂点(※)あります。
これをどう結ぶか、を考えないとなりません。
今回のサンプルではシンプルに、全頂点の平均位置を求め、それと、新頂点を順番に結んで、ピザを切り分けたような形でポリゴンを形成するような処理になっています。
※ ... 最初、頂点検索のアルゴリズムが分かりづらかったのですが、上のように8頂点を見つけ出す処理でした。が、実はこのアルゴリズムの場合、重複した、同じ位置にある点についてもポリゴンを形成していて、若干冗長な処理になっているようです。(つまり、同じ位置に重なるように2枚のカット平面が存在することになる)
ただ、負荷的にとても増える、というものでもないのでこのままにしているのだと思います。(Simple Cutって言ってるし)
上記はキューブの断面ではないですが、青い8頂点が新頂点として生成されたもの、として考えてください。
これの平均位置を取ると中心あたりになり、オレンジの点($c$)となります。
あとはこれを、順番に結んでいけば切断面のポリゴンが形成できる、というわけです。
順番とは、「$1, 2, c$」,「$2, 3, c$」,「$3, 4, c$」... という具合です。
最後にこの、切断面のポリゴンを形成するコードを以下に示します。
/// <summary>
/// カット面を埋める
/// </summary>
/// <param name="vertices">ポリゴンを形成する頂点リスト</param>
static void FillCap(List<Vector3> vertices)
{
// center of the cap
// カット平面の中心点を計算する
Vector3 center = Vector3.zero;
// 引数で渡された頂点位置をすべて合計する
foreach(Vector3 point in vertices)
{
center += point;
}
// それを頂点数の合計で割り、中心とする
center = center / vertices.Count;
// you need an axis based on the cap
// カット平面をベースにしたupward
Vector3 upward = Vector3.zero;
// 90 degree turn
// カット平面の法線を利用して、「上」方向を求める
// 具体的には、平面の左側を上として利用する
upward.x = blade.normal.y;
upward.y = -blade.normal.x;
upward.z = blade.normal.z;
// 法線と「上方向」から、横軸を算出
Vector3 left = Vector3.Cross(blade.normal, upward);
Vector3 displacement = Vector3.zero;
Vector3 newUV1 = Vector3.zero;
Vector3 newUV2 = Vector3.zero;
// 引数で与えられた頂点分ループを回す
for (int i = 0; i < vertices.Count; i++)
{
// 計算で求めた中心点から、各頂点への方向ベクトル
displacement = vertices[i] - center;
// 新規生成するポリゴンのUV座標を求める。
// displacementが中心からのベクトルのため、UV的な中心である0.5をベースに、内積を使ってUVの最終的な位置を得る
newUV1 = Vector3.zero;
newUV1.x = 0.5f + Vector3.Dot(displacement, left);
newUV1.y = 0.5f + Vector3.Dot(displacement, upward);
newUV1.z = 0.5f + Vector3.Dot(displacement, blade.normal);
// 次の頂点。ただし、最後の頂点の次は最初の頂点を利用するため、若干トリッキーな指定方法をしている(% vertices.Count)
displacement = vertices[(i + 1) % vertices.Count] - center;
newUV2 = Vector3.zero;
newUV2.x = 0.5f + Vector3.Dot(displacement, left);
newUV2.y = 0.5f + Vector3.Dot(displacement, upward);
newUV2.z = 0.5f + Vector3.Dot(displacement, blade.normal);
// uvs.Add(new Vector2(relativePosition.x, relativePosition.y));
// normals.Add(blade.normal);
// 左側のポリゴンとして、求めたUVを利用してトライアングルを追加
left_side.AddTriangle(
new Vector3[]{
vertices[i],
vertices[(i + 1) % vertices.Count],
center
},
new Vector3[]{
-blade.normal,
-blade.normal,
-blade.normal
},
new Vector2[]{
newUV1,
newUV2,
new Vector2(0.5f, 0.5f)
},
-blade.normal,
left_side.subIndices.Count - 1 // カット面。最後のサブメッシュとしてトライアングルを追加
);
// 右側のトライアングル。基本は左側と同じだが、法線だけ逆向き。
right_side.AddTriangle(
new Vector3[]{
vertices[i],
vertices[(i + 1) % vertices.Count],
center
},
new Vector3[]{
blade.normal,
blade.normal,
blade.normal
},
new Vector2[]{
newUV1,
newUV2,
new Vector2(0.5f, 0.5f)
},
blade.normal,
right_side.subIndices.Count - 1 // カット面。最後のサブメッシュとしてトライアングルを追加
);
}
}
以上が、メッシュの切断を行っているコードの解説となります。
サンプルコード
下のコードは、上で解説したコードの全文です。
自分の理解のために各処理について日本語でコメントを入れているので、分かりづらい点などはそちらも合わせて見てもらうと理解が促されるかもしれません。
using UnityEngine;
using System.Collections;
using System.Collections.Generic;
namespace BLINDED_AM_ME
{
public class MeshCut
{
public class MeshCutSide
{
public List<Vector3> vertices = new List<Vector3>();
public List<Vector3> normals = new List<Vector3>();
public List<Vector2> uvs = new List<Vector2>();
public List<int> triangles = new List<int>();
public List<List<int>> subIndices = new List<List<int>>();
public void ClearAll()
{
vertices.Clear();
normals.Clear();
uvs.Clear();
triangles.Clear();
subIndices.Clear();
}
/// <summary>
/// トライアングルとして3頂点を追加
/// ※ 頂点情報は元のメッシュからコピーする
/// </summary>
/// <param name="p1">頂点1</param>
/// <param name="p2">頂点2</param>
/// <param name="p3">頂点3</param>
/// <param name="submesh">対象のサブメシュ</param>
public void AddTriangle(int p1, int p2, int p3, int submesh)
{
// triangle index order goes 1,2,3,4....
// 頂点配列のカウント。随時追加されていくため、ベースとなるindexを定義する。
// ※ AddTriangleが呼ばれるたびに頂点数は増えていく。
int base_index = vertices.Count;
// 対象サブメッシュのインデックスに追加していく
subIndices[submesh].Add(base_index + 0);
subIndices[submesh].Add(base_index + 1);
subIndices[submesh].Add(base_index + 2);
// 三角形郡の頂点を設定
triangles.Add(base_index + 0);
triangles.Add(base_index + 1);
triangles.Add(base_index + 2);
// 対象オブジェクトの頂点配列から頂点情報を取得し設定する
// (victim_meshはstaticメンバなんだけどいいんだろうか・・)
vertices.Add(victim_mesh.vertices[p1]);
vertices.Add(victim_mesh.vertices[p2]);
vertices.Add(victim_mesh.vertices[p3]);
// 同様に、対象オブジェクトの法線配列から法線を取得し設定する
normals.Add(victim_mesh.normals[p1]);
normals.Add(victim_mesh.normals[p2]);
normals.Add(victim_mesh.normals[p3]);
// 同様に、UVも。
uvs.Add(victim_mesh.uv[p1]);
uvs.Add(victim_mesh.uv[p2]);
uvs.Add(victim_mesh.uv[p3]);
}
/// <summary>
/// トライアングルを追加する
/// ※ オーバーロードしている他メソッドとは異なり、引数の値で頂点(ポリゴン)を追加する
/// </summary>
/// <param name="points3">トライアングルを形成する3頂点</param>
/// <param name="normals3">3頂点の法線</param>
/// <param name="uvs3">3頂点のUV</param>
/// <param name="faceNormal">ポリゴンの法線</param>
/// <param name="submesh">サブメッシュID</param>
public void AddTriangle(Vector3[] points3, Vector3[] normals3, Vector2[] uvs3, Vector3 faceNormal, int submesh)
{
// 引数の3頂点から法線を計算
Vector3 calculated_normal = Vector3.Cross((points3[1] - points3[0]).normalized, (points3[2] - points3[0]).normalized);
int p1 = 0;
int p2 = 1;
int p3 = 2;
// 引数で指定された法線と逆だった場合はインデックスの順番を逆順にする(つまり面を裏返す)
if (Vector3.Dot(calculated_normal, faceNormal) < 0)
{
p1 = 2;
p2 = 1;
p3 = 0;
}
int base_index = vertices.Count;
subIndices[submesh].Add(base_index + 0);
subIndices[submesh].Add(base_index + 1);
subIndices[submesh].Add(base_index + 2);
triangles.Add(base_index + 0);
triangles.Add(base_index + 1);
triangles.Add(base_index + 2);
vertices.Add(points3[p1]);
vertices.Add(points3[p2]);
vertices.Add(points3[p3]);
normals.Add(normals3[p1]);
normals.Add(normals3[p2]);
normals.Add(normals3[p3]);
uvs.Add(uvs3[p1]);
uvs.Add(uvs3[p2]);
uvs.Add(uvs3[p3]);
}
}
private static MeshCutSide left_side = new MeshCutSide();
private static MeshCutSide right_side = new MeshCutSide();
private static Plane blade;
private static Mesh victim_mesh;
// capping stuff
private static List<Vector3> new_vertices = new List<Vector3>();
/// <summary>
/// Cut the specified victim, blade_plane and capMaterial.
/// (指定された「victim」をカットする。ブレード(平面)とマテリアルから切断を実行する)
/// </summary>
/// <param name="victim">Victim.</param>
/// <param name="blade_plane">Blade plane.</param>
/// <param name="capMaterial">Cap material.</param>
public static GameObject[] Cut(GameObject victim, Vector3 anchorPoint, Vector3 normalDirection, Material capMaterial)
{
// set the blade relative to victim
// victimから相対的な平面(ブレード)をセット
// 具体的には、対象オブジェクトのローカル座標での平面の法線と位置から平面を生成する
blade = new Plane(
victim.transform.InverseTransformDirection(-normalDirection),
victim.transform.InverseTransformPoint(anchorPoint)
);
// get the victims mesh
// 対象のメッシュを取得
victim_mesh = victim.GetComponent<MeshFilter>().mesh;
// reset values
// 新しい頂点郡
new_vertices.Clear();
// 平面より左の頂点郡(MeshCutSide)
left_side.ClearAll();
//平面より右の頂点郡(MeshCutSide)
right_side.ClearAll();
// ここでの「3」はトライアングル?
bool[] sides = new bool[3];
int[] indices;
int p1,p2,p3;
// go throught the submeshes
// サブメッシュの数だけループ
for (int sub = 0; sub < victim_mesh.subMeshCount; sub++)
{
// サブメッシュのインデックス数を取得
indices = victim_mesh.GetIndices(sub);
// List<List<int>>型のリスト。サブメッシュ一つ分のインデックスリスト
left_side.subIndices.Add(new List<int>()); // 左
right_side.subIndices.Add(new List<int>()); // 右
// サブメッシュのインデックス数分ループ
for (int i = 0; i < indices.Length; i += 3)
{
// p1 - p3のインデックスを取得。つまりトライアングル
p1 = indices[i + 0];
p2 = indices[i + 1];
p3 = indices[i + 2];
// それぞれ評価中のメッシュの頂点が、冒頭で定義された平面の左右どちらにあるかを評価。
// `GetSide` メソッドによりboolを得る。
sides[0] = blade.GetSide(victim_mesh.vertices[p1]);
sides[1] = blade.GetSide(victim_mesh.vertices[p2]);
sides[2] = blade.GetSide(victim_mesh.vertices[p3]);
// whole triangle
// 頂点0と頂点1および頂点2がどちらも同じ側にある場合はカットしない
if (sides[0] == sides[1] && sides[0] == sides[2])
{
if (sides[0])
{ // left side
// GetSideメソッドでポジティブ(true)の場合は左側にあり
left_side.AddTriangle(p1, p2, p3, sub);
}
else
{
right_side.AddTriangle(p1, p2, p3, sub);
}
}
else
{ // cut the triangle
// そうではなく、どちらかの点が平面の反対側にある場合はカットを実行する
Cut_this_Face(sub, sides, p1, p2, p3);
}
}
}
// 設定されているマテリアル配列を取得
Material[] mats = victim.GetComponent<MeshRenderer>().sharedMaterials;
// 取得したマテリアル配列の最後のマテリアルが、カット面のマテリアルでない場合
if (mats[mats.Length - 1].name != capMaterial.name)
{ // add cap indices
// カット面用のインデックス配列を追加?
left_side.subIndices.Add(new List<int>());
right_side.subIndices.Add(new List<int>());
// カット面分増やしたマテリアル配列を準備
Material[] newMats = new Material[mats.Length + 1];
// 既存のものを新しい配列にコピー
mats.CopyTo(newMats, 0);
// 新しいマテリアル配列の最後に、カット面用マテリアルを追加
newMats[mats.Length] = capMaterial;
// 生成したマテリアルリストを再設定
mats = newMats;
}
// cap the opennings
// カット開始
Capping();
// Left Mesh
// 左側のメッシュを生成
// MeshCutSideクラスのメンバから各値をコピー
Mesh left_HalfMesh = new Mesh();
left_HalfMesh.name = "Split Mesh Left";
left_HalfMesh.vertices = left_side.vertices.ToArray();
left_HalfMesh.triangles = left_side.triangles.ToArray();
left_HalfMesh.normals = left_side.normals.ToArray();
left_HalfMesh.uv = left_side.uvs.ToArray();
left_HalfMesh.subMeshCount = left_side.subIndices.Count;
for (int i = 0; i < left_side.subIndices.Count; i++)
{
left_HalfMesh.SetIndices(left_side.subIndices[i].ToArray(), MeshTopology.Triangles, i);
}
// Right Mesh
// 右側のメッシュも同様に生成
Mesh right_HalfMesh = new Mesh();
right_HalfMesh.name = "Split Mesh Right";
right_HalfMesh.vertices = right_side.vertices.ToArray();
right_HalfMesh.triangles = right_side.triangles.ToArray();
right_HalfMesh.normals = right_side.normals.ToArray();
right_HalfMesh.uv = right_side.uvs.ToArray();
right_HalfMesh.subMeshCount = right_side.subIndices.Count;
for (int i = 0; i < right_side.subIndices.Count; i++)
{
right_HalfMesh.SetIndices(right_side.subIndices[i].ToArray(), MeshTopology.Triangles, i);
}
// assign the game objects
// 元のオブジェクトを左側のオブジェクトに
victim.name = "left side";
victim.GetComponent<MeshFilter>().mesh = left_HalfMesh;
// 右側のオブジェクトは新規作成
GameObject leftSideObj = victim;
GameObject rightSideObj = new GameObject("right side", typeof(MeshFilter), typeof(MeshRenderer));
rightSideObj.transform.position = victim.transform.position;
rightSideObj.transform.rotation = victim.transform.rotation;
rightSideObj.GetComponent<MeshFilter>().mesh = right_HalfMesh;
// assign mats
// 新規生成したマテリアルリストをそれぞれのオブジェクトに適用する
leftSideObj.GetComponent<MeshRenderer>().materials = mats;
rightSideObj.GetComponent<MeshRenderer>().materials = mats;
// 左右のGameObjectの配列を返す
return new GameObject[]{ leftSideObj, rightSideObj };
}
/// <summary>
/// カットを実行する。ただし、実際のメッシュの操作ではなく、あくまで頂点の振り分け、事前準備としての実行
/// </summary>
/// <param name="submesh">サブメッシュのインデックス</param>
/// <param name="sides">評価した3頂点の左右情報</param>
/// <param name="index1">頂点1</param>
/// <param name="index2">頂点2</param>
/// <param name="index3">頂点3</param>
static void Cut_this_Face(int submesh, bool[] sides, int index1, int index2, int index3)
{
// 左右それぞれの情報を保持するための配列郡
Vector3[] leftPoints = new Vector3[2];
Vector3[] leftNormals = new Vector3[2];
Vector2[] leftUvs = new Vector2[2];
Vector3[] rightPoints = new Vector3[2];
Vector3[] rightNormals = new Vector3[2];
Vector2[] rightUvs = new Vector2[2];
bool didset_left = false;
bool didset_right = false;
// 3頂点分繰り返す
// 処理内容としては、左右を判定して、左右の配列に3頂点を振り分ける処理を行っている
int p = index1;
for (int side = 0; side < 3; side++)
{
switch(side)
{
case 0:
p = index1;
break;
case 1:
p = index2;
break;
case 2:
p = index3;
break;
}
// sides[side]がtrue、つまり左側の場合
if (sides[side])
{
// すでに左側の頂点が設定されているか(3頂点が左右に振り分けられるため、必ず左右どちらかは2つの頂点を持つことになる)
if (!didset_left)
{
didset_left = true;
// ここは0,1ともに同じ値にしているのは、続く処理で
// leftPoints[0,1]の値を使って分割点を求める処理をしているため。
// つまり、アクセスされる可能性がある
// 頂点の設定
leftPoints[0] = victim_mesh.vertices[p];
leftPoints[1] = leftPoints[0];
// UVの設定
leftUvs[0] = victim_mesh.uv[p];
leftUvs[1] = leftUvs[0];
// 法線の設定
leftNormals[0] = victim_mesh.normals[p];
leftNormals[1] = leftNormals[0];
}
else
{
// 2頂点目の場合は2番目に直接頂点情報を設定する
leftPoints[1] = victim_mesh.vertices[p];
leftUvs[1] = victim_mesh.uv[p];
leftNormals[1] = victim_mesh.normals[p];
}
}
else
{
// 左と同様の操作を右にも行う
if (!didset_right)
{
didset_right = true;
rightPoints[0] = victim_mesh.vertices[p];
rightPoints[1] = rightPoints[0];
rightUvs[0] = victim_mesh.uv[p];
rightUvs[1] = rightUvs[0];
rightNormals[0] = victim_mesh.normals[p];
rightNormals[1] = rightNormals[0];
}
else
{
rightPoints[1] = victim_mesh.vertices[p];
rightUvs[1] = victim_mesh.uv[p];
rightNormals[1] = victim_mesh.normals[p];
}
}
}
// 分割された点の比率計算のための距離
float normalizedDistance = 0f;
// 距離
float distance = 0f;
// ---------------------------
// 左側の処理
// 定義した面と交差する点を探す。
// つまり、平面によって分割される点を探す。
// 左の点を起点に、右の点に向けたレイを飛ばし、その分割点を探る。
blade.Raycast(new Ray(leftPoints[0], (rightPoints[0] - leftPoints[0]).normalized), out distance);
// 見つかった交差点を、頂点間の距離で割ることで、分割点の左右の割合を算出する
normalizedDistance = distance / (rightPoints[0] - leftPoints[0]).magnitude;
// カット後の新頂点に対する処理。フラグメントシェーダでの補完と同じく、分割した位置に応じて適切に補完した値を設定する
Vector3 newVertex1 = Vector3.Lerp(leftPoints[0], rightPoints[0], normalizedDistance);
Vector2 newUv1 = Vector2.Lerp(leftUvs[0], rightUvs[0], normalizedDistance);
Vector3 newNormal1 = Vector3.Lerp(leftNormals[0] , rightNormals[0], normalizedDistance);
// 新頂点郡に新しい頂点を追加
new_vertices.Add(newVertex1);
// ---------------------------
// 右側の処理
blade.Raycast(new Ray(leftPoints[1], (rightPoints[1] - leftPoints[1]).normalized), out distance);
normalizedDistance = distance / (rightPoints[1] - leftPoints[1]).magnitude;
Vector3 newVertex2 = Vector3.Lerp(leftPoints[1], rightPoints[1], normalizedDistance);
Vector2 newUv2 = Vector2.Lerp(leftUvs[1], rightUvs[1], normalizedDistance);
Vector3 newNormal2 = Vector3.Lerp(leftNormals[1] , rightNormals[1], normalizedDistance);
// 新頂点郡に新しい頂点を追加
new_vertices.Add(newVertex2);
// 計算された新しい頂点を使って、新トライアングルを左右ともに追加する
// memo: どう分割されても、左右どちらかは1つの三角形になる気がするけど、縮退三角形的な感じでとにかく2つずつ追加している感じだろうか?
left_side.AddTriangle(
new Vector3[]{leftPoints[0], newVertex1, newVertex2},
new Vector3[]{leftNormals[0], newNormal1, newNormal2 },
new Vector2[]{leftUvs[0], newUv1, newUv2},
newNormal1,
submesh
);
left_side.AddTriangle(
new Vector3[]{leftPoints[0], leftPoints[1], newVertex2},
new Vector3[]{leftNormals[0], leftNormals[1], newNormal2},
new Vector2[]{leftUvs[0], leftUvs[1], newUv2},
newNormal2,
submesh
);
right_side.AddTriangle(
new Vector3[]{rightPoints[0], newVertex1, newVertex2},
new Vector3[]{rightNormals[0], newNormal1, newNormal2},
new Vector2[]{rightUvs[0], newUv1, newUv2},
newNormal1,
submesh
);
right_side.AddTriangle(
new Vector3[]{rightPoints[0], rightPoints[1], newVertex2},
new Vector3[]{rightNormals[0], rightNormals[1], newNormal2},
new Vector2[]{rightUvs[0], rightUvs[1], newUv2},
newNormal2,
submesh
);
}
private static List<Vector3> capVertTracker = new List<Vector3>();
private static List<Vector3> capVertpolygon = new List<Vector3>();
/// <summary>
/// カットを実行
/// </summary>
static void Capping()
{
// カット用頂点追跡リスト
// 具体的には新頂点全部に対する調査を行う。その過程で調査済みをマークする目的で利用する。
capVertTracker.Clear();
// 新しく生成した頂点分だけループする=全新頂点に対してポリゴンを形成するため調査を行う
// 具体的には、カット面を構成するポリゴンを形成するため、カット時に重複した頂点を網羅して「面」を形成する頂点を調査する
for (int i = 0; i < new_vertices.Count; i++)
{
// 対象頂点がすでに調査済みのマークされて(追跡配列に含まれて)いたらスキップ
if (capVertTracker.Contains(new_vertices[i]))
{
continue;
}
// カット用ポリゴン配列をクリア
capVertpolygon.Clear();
// 調査頂点と次の頂点をポリゴン配列に保持する
capVertpolygon.Add(new_vertices[i + 0]);
capVertpolygon.Add(new_vertices[i + 1]);
// 追跡配列に自身と次の頂点を追加する(調査済みのマークをつける)
capVertTracker.Add(new_vertices[i + 0]);
capVertTracker.Add(new_vertices[i + 1]);
// 重複頂点がなくなるまでループし調査する
bool isDone = false;
while (!isDone)
{
isDone = true;
// 新頂点郡をループし、「面」を構成する要因となる頂点をすべて抽出する。抽出が終わるまでループを繰り返す
// 2頂点ごとに調査を行うため、ループは2単位ですすめる
for (int k = 0; k < new_vertices.Count; k += 2)
{ // go through the pairs
// ペアとなる頂点を探す
// ここでのペアとは、いちトライアングルから生成される新頂点のペア。
// トライアングルからは必ず2頂点が生成されるため、それを探す。
// また、全ポリゴンに対して分割点を生成しているため、ほぼ必ず、まったく同じ位置に存在する、別トライアングルの分割頂点が存在するはずである。
if (new_vertices[k] == capVertpolygon[capVertpolygon.Count - 1] && !capVertTracker.Contains(new_vertices[k + 1]))
{ // if so add the other
// ペアの頂点が見つかったらそれをポリゴン配列に追加し、
// 調査済マークをつけて、次のループ処理に回す
isDone = false;
capVertpolygon.Add(new_vertices[k + 1]);
capVertTracker.Add(new_vertices[k + 1]);
}
else if (new_vertices[k + 1] == capVertpolygon[capVertpolygon.Count - 1] && !capVertTracker.Contains(new_vertices[k]))
{ // if so add the other
isDone = false;
capVertpolygon.Add(new_vertices[k]);
capVertTracker.Add(new_vertices[k]);
}
}
}
// 見つかった頂点郡を元に、ポリゴンを形成する
FillCap(capVertpolygon);
}
}
/// <summary>
/// カット面を埋める?
/// </summary>
/// <param name="vertices">ポリゴンを形成する頂点リスト</param>
static void FillCap(List<Vector3> vertices)
{
// center of the cap
// カット平面の中心点を計算する
Vector3 center = Vector3.zero;
// 引数で渡された頂点位置をすべて合計する
foreach(Vector3 point in vertices)
{
center += point;
}
// それを頂点数の合計で割り、中心とする
center = center / vertices.Count;
// you need an axis based on the cap
// カット平面をベースにしたupward
Vector3 upward = Vector3.zero;
// 90 degree turn
// カット平面の法線を利用して、「上」方向を求める
// 具体的には、平面の左側を上として利用する
upward.x = blade.normal.y;
upward.y = -blade.normal.x;
upward.z = blade.normal.z;
// 法線と「上方向」から、横軸を算出
Vector3 left = Vector3.Cross(blade.normal, upward);
Vector3 displacement = Vector3.zero;
Vector3 newUV1 = Vector3.zero;
Vector3 newUV2 = Vector3.zero;
// 引数で与えられた頂点分ループを回す
for (int i = 0; i < vertices.Count; i++)
{
// 計算で求めた中心点から、各頂点への方向ベクトル
displacement = vertices[i] - center;
// 新規生成するポリゴンのUV座標を求める。
// displacementが中心からのベクトルのため、UV的な中心である0.5をベースに、内積を使ってUVの最終的な位置を得る
newUV1 = Vector3.zero;
newUV1.x = 0.5f + Vector3.Dot(displacement, left);
newUV1.y = 0.5f + Vector3.Dot(displacement, upward);
newUV1.z = 0.5f + Vector3.Dot(displacement, blade.normal);
// 次の頂点。ただし、最後の頂点の次は最初の頂点を利用するため、若干トリッキーな指定方法をしている(% vertices.Count)
displacement = vertices[(i + 1) % vertices.Count] - center;
newUV2 = Vector3.zero;
newUV2.x = 0.5f + Vector3.Dot(displacement, left);
newUV2.y = 0.5f + Vector3.Dot(displacement, upward);
newUV2.z = 0.5f + Vector3.Dot(displacement, blade.normal);
// uvs.Add(new Vector2(relativePosition.x, relativePosition.y));
// normals.Add(blade.normal);
// 左側のポリゴンとして、求めたUVを利用してトライアングルを追加
left_side.AddTriangle(
new Vector3[]{
vertices[i],
vertices[(i + 1) % vertices.Count],
center
},
new Vector3[]{
-blade.normal,
-blade.normal,
-blade.normal
},
new Vector2[]{
newUV1,
newUV2,
new Vector2(0.5f, 0.5f)
},
-blade.normal,
left_side.subIndices.Count - 1 // カット面。最後のサブメッシュとしてトライアングルを追加
);
// 右側のトライアングル。基本は左側と同じだが、法線だけ逆向き。
right_side.AddTriangle(
new Vector3[]{
vertices[i],
vertices[(i + 1) % vertices.Count],
center
},
new Vector3[]{
blade.normal,
blade.normal,
blade.normal
},
new Vector2[]{
newUV1,
newUV2,
new Vector2(0.5f, 0.5f)
},
blade.normal,
right_side.subIndices.Count - 1 // カット面。最後のサブメッシュとしてトライアングルを追加
);
}
}
}
}