モダンな深層距離学習 (deep metric learning) 手法: SphereFace, CosFace, ArcFace

はじめに

顔認識 (face recognition) 等の個体識別問題において、距離学習は非常に重要です。ここで個体識別問題というのは、顔認識を例に取ると下記のようなものです。

• 2つの顔画像ペアが与えられた際にその顔画像ペアが同一人物のものであるかを判定する1:1認証
• N人の顔画像データが予め与えられた状態で、個人が特定されていない顔画像が入力された際に、その顔画像がN人のうちどれであるか、またはどれでもないかを判定する1:N認証

何故距離学習が重要かというと、クラス分類問題とは異なりクラス数が不定で各クラスに属する画像を事前に得ることができず¹、クラス分類問題として解くことができないためである。このため、何かしらの学習済みモデルを利用して各画像から特徴ベクトルを抽出し、その特徴ベクトル間の距離がしきい値以下であれば同一人物、しきい値より大きければ異なる人物と判定する（コサイン類似度等の類似度を利用する場合は逆）アプローチを取ることになります。

これを実現するためには、利用する特徴ベクトル間の距離が、同一人物のものは小さく、他人同士のものは大きくなることが必要です。検索の問題であればこれだけでも良いのですが、認識の場合には更に、同一であるかのしきい値が、どの特徴ベクトルペアに対しても一律に利用できることが要求されます。

これまで、深層学習を用いて特徴ベクトルを抽出するコンテキストにおいては、contrastive lossやtriplet lossを利用することが主流でした。これらについてはこちらの記事が詳しいです。

そんな折、顔認識に関するサーベイ論文を見て下記のようなツイートをしました。

これめっちゃ素敵な表なんだけど、見てると最近はcontrastive lossとかtriplet lossとかあまり使われないのかな？という気持ちになるけど、単にそれ使うと論文が通らないだけではとも思ってて、最近提案されているロスが本質的に良いのか分からない https://t.co/O92DtiRzXL pic.twitter.com/ERqsCknZne

— Yusuke Uchida (@yu4u) 2019年2月13日

色々提案されているけどどうせ結局contrastive lossとかtriplet lossを使っておけばいいんでしょ、と思いながら論文を読んでみると、完全にその認識が浦島太郎状態だったので、最近のSphereFace, CosFace, ArcFaceといった手法を紹介します。

ちなみにArcFaceを実際にKaggleの課題で使ってみて、本当にうまくいったので、顔以外の様々な問題に適用できると思います。

落書きコンペに引き続き1週間チャレンジみたいになっちゃった🐳コンペ、18位フィニッシュでした。当日学習終わった1回もサブミットしたことのないモデルのアンサンブルでLB見れてなかったのでshake-upはすると思っていたけど、もうちょっとTTAとアンサンブル頑張れば良かった… https://t.co/fUfJ2BV3jC

— Yusuke Uchida (@yu4u) 2019年3月1日

SphereFace, CosFace, ArcFace

さて、肝心のこれらの手法、何が嬉しいかというと、「通常のクラス分類問題を学習させるだけで距離学習が実現できる」につきます。
Contrastive LossやTriplet Lossの学習では、異なるクラスなのに距離が近くなってしまっているhard negative pairをうまくサンプリングしないといけなかったり、そもそも学習が不安定だったりします。
これに対し、SphereFace, CosFace, ArcFace等の手法は、学習が容易なクラス分類モデルに1層独自のレイヤを追加するだけで、通常のクラス分類問題として学習が可能です。当然、ロスもcross entropyのままで良いのです。何度でも言います。クラス分類問題として学習できるんです！

Softmax Cross Entropy

SphereFace, CosFace, ArcFaceの説明に入る前に、通常のsoftmax cross entropyを復習しておきましょう。

上記の図は、softmax cross entropyを算出している部分を図示したものとなります。左上がCNN（でなくても良いですが）で特徴抽出を行っている部分で、$i$番目の学習サンプルについて、softmaxをかける直前の全結合層への入力となる$D$次元ベクトル$x_i$を抽出しています。

この$x_i$に対して、最後の全結合層の重み$W \in \mathbb{R}^{D \times C}$をかけ、バイアス項$b$を足し、正規化されていないlogits $e = W^T x_i + b$を算出します。ここで$C$はクラス数です。そしてこのlogitsにsoftmaxをかけ、予測確率分布を出力します。$j$番目のクラスの確率は、$\frac{\exp(e_j)}{\sum_k \exp(e_k)}$となります。

Cross entropy lossは、正解クラスに対する予測確率のみに依存し、$i$番目のサンプルに対するロスは$-\log \frac{\exp(e_{y_i})}{\sum_k \exp(e_k)}$と定義されます。ここで$y_i$は、$i$番目のサンプルの正解クラスIDです。このロスを全サンプルに対して合計しつつ、logits $e$を展開して書いてしまうと、
$$
-\frac{1}{N} \sum_{i=1}^N \log \frac{\exp (W^T_{y_i} x_i + b_{y_i})}{\sum_k \exp (W^T_k x_i + b_k)}.
$$
となります。この展開式を利用して説明している論文が多いのでまずはここを抑えておきましょう。

ArcFace

では実際の手法を説明していきます。様々な亜種が存在しますが、現在の最終型であるArcFaceかCosFaceをまずは理解するのが一番早いかと思いますので、ここではArcFaceを解説します。

下の図がArcFaceの全体像です。

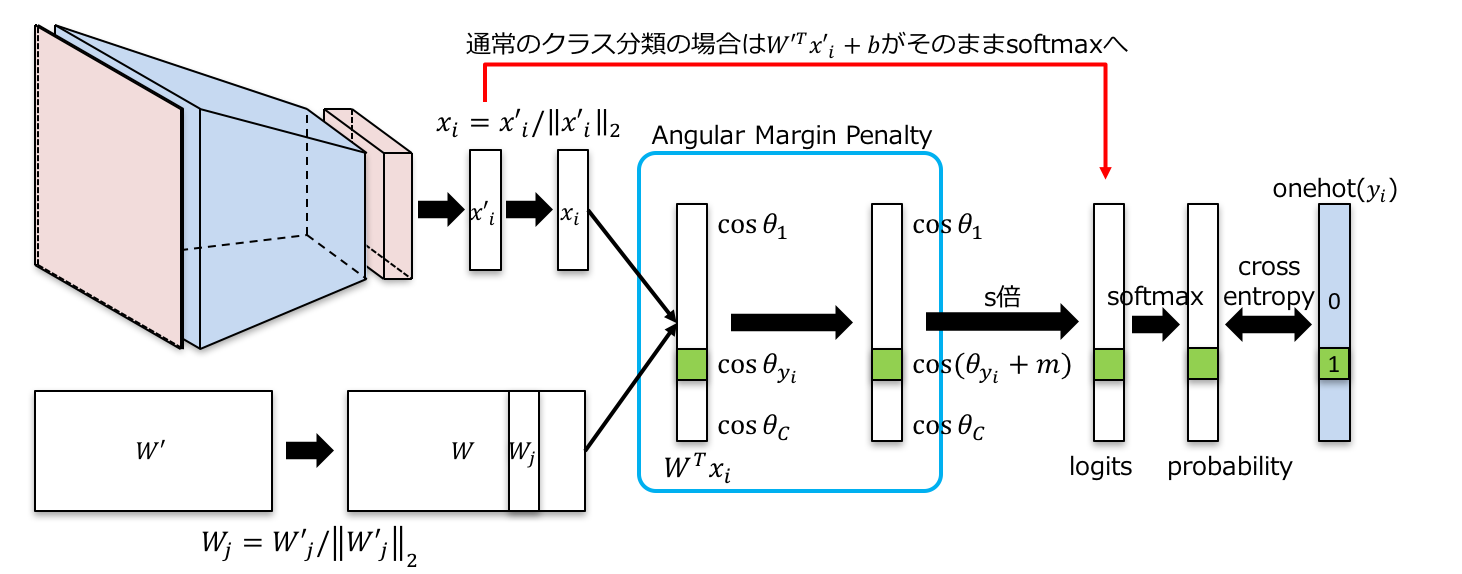
前述した通常のsoftmax cross entropyと比較すると、最後の全結合層で色々処理が増えていることが分かります。ごちゃごちゃしていますが、やっていることはシンプルかつstraight forwardです。

まず分かりやすい差分として、CNNからの特徴ベクトル$x'$が、$L_2$正規化されています。これは、難しいサンプルについて、モデルが単純に$x'$のノルムを小さくするように学習してしまう（一様分布に近い出力を出そうとする）ことを防ぎ、難しいサンプルについてもちゃんと学習を行わせる効果があります²。

また、全結合層の重み$W'$についても、列ごとに$L_2$正規化が行われ、更にバイアス項は$b=0$となっています。これにより、$x$と$W$との内積で得られるlogitsの$j$番目のクラスに対応する値$W_j^T x$が、$x$と$W_j$のなす角を$\theta$を用いて$\cos \theta_j$で表すことができます。このモデルでは、$W$, $x$と出力結果の関係を直感的に理解することができます。すなわち、$W_j ; (1 \le j \le C)$は、各クラスを代表するベクトルで、このベクトルと$x$のなす角$\theta_j$が最も小さいクラス$j$に分類していることにほかなりません。

次に、肝心のAngular Margin Penalty部分についてです。ここで何をやっているかというと、「正解クラス$y_i$に対応するlogits $\cos \theta_j$のみ」に対して、$\cos (\theta_j + m)$ ($m>0$) という変更（ペナルティ）を加えています。こうすると、当然正解クラスに対応するlogitsの値が小さくなってしまいます。通常の学習では、とりあえず正解クラスの代表ベクトル$W_{y_i}$とのなす角$\theta_{y_i}$が、他のクラスのものより小さくなれば良いやくらいの感覚だったのが、なんと他のどのクラスの代表ベクトルとの角度よりも、$\theta_{y_i}$が$m$以上のマージンを持って小さくないと駄目ということになってしまいました！このペナルティにより、モデルは頑張って特徴ベクトル$x$のクラス内分散を小さくし、クラス間分散を大きくして、このマージンを稼ごうと頑張るわけです。これがSphereFace, CosFace, ArcFace系の手法の本質になります。

最後にこの$\cos \theta$の値は$s$ ($s > 1$)倍されてsoftmaxへ送られます。これは今回のようにlogitsの値が小さすぎるとsoftmaxが機能しなくなるために調節を行っている処理になります。softmaxの温度パラメータ$T$を調節していることと同値です（$s = 1/T$）（記事の後半に簡単な説明があります）。

ArcFaceのロスを書き下すと下記になります。いきなりこの式が出てくると！？となりますが、上記の流れを理解していると、自然に理解できると思います。

$$
-\frac{1}{N} \sum_{i=1}^N \log \frac{\exp (s \cos (\theta_{y_i} + m))}{\exp (s \cos (\theta_{y_i} + m)) + \sum_{k \neq y_i} \exp (s \cos \theta_k)}.
$$

上記のような処理を加えたモデルを通常のクラス分類として学習させることで、内部では頑張って特徴ベクトル$x$のクラス内分散を小さくし、クラス間分散を大きくするような学習が実現できるのです。実際に利用する場合には、正規化された特徴ベクトルを$x$抽出し、それらのコサイン類似度によってサンプル間の類似度を算出することができます。

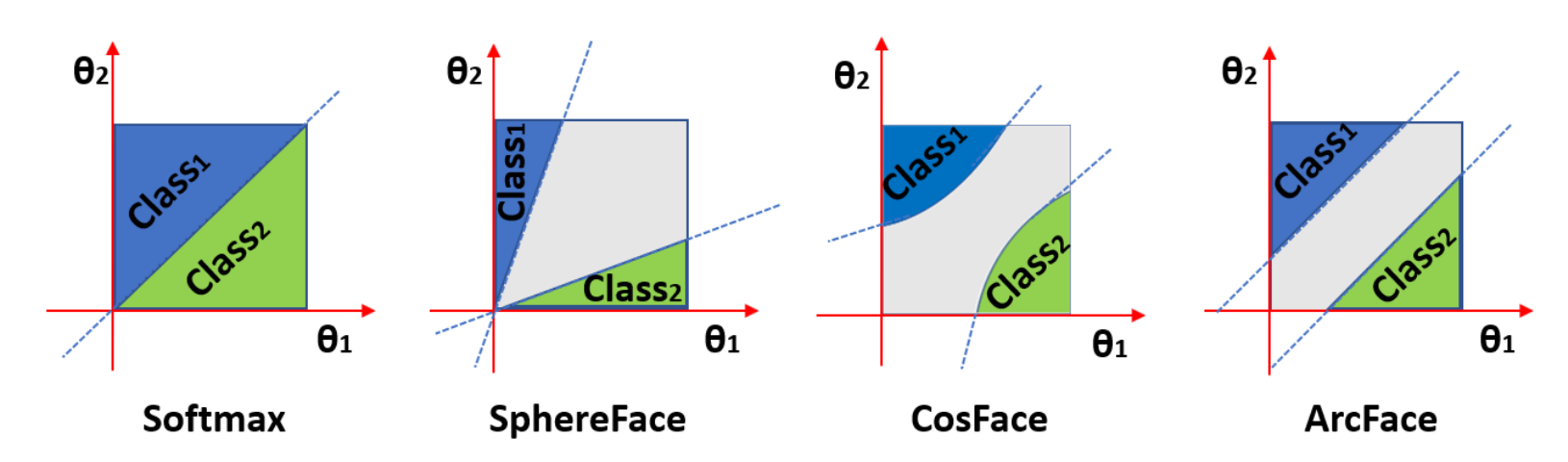
SphereFace, CosFace, ArcFaceの違い

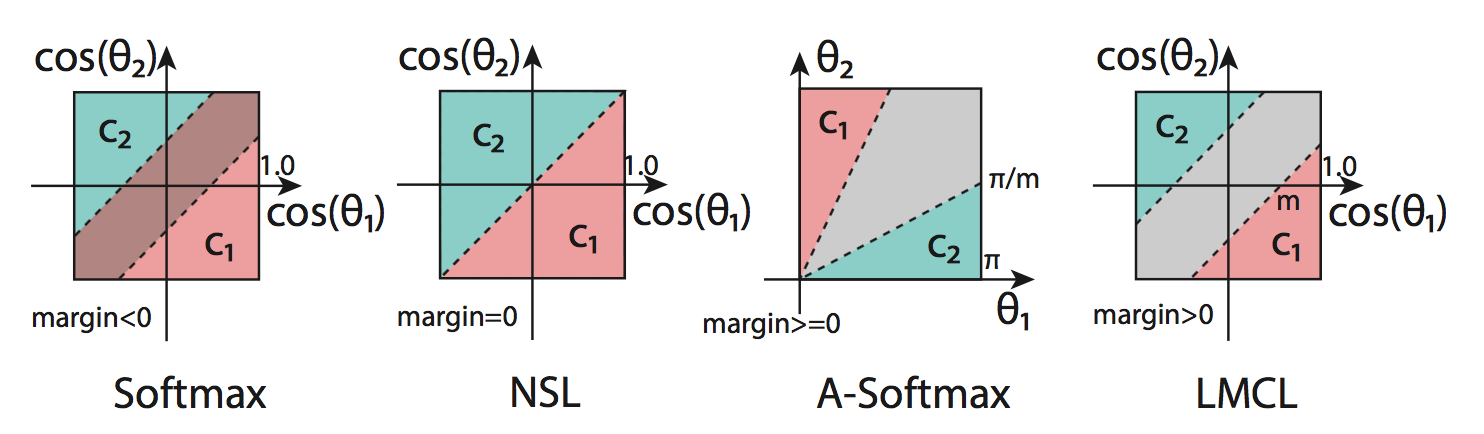
これらの手法の違いはペナルティのかけ方にあります。logitsの値に対して$\cos (m_1\theta_{y_i} + m2) - m_3$のようなペナルティを定義すると、$m_1$がSphereFace、$m_2$がArcFace、$m_3$がCosFaceに対応します。CosFace, ArcFaceの違いは、どの空間で綺麗にマージンが定義されるかの違いです。

CosFaceの論文には下記のような図が載っています。NSLはペナルティなしの場合、A-SoftmaxはSphereFaceです。

ArcFaceには下記のような図が載っています。

以上、本文終わり。以下はよもやま話。

関連論文について

さて、関連論文についても面白いので紹介します。まず、softmaxで特徴ベクトルを正規化して学習しようと提案した文献が2017年3月にarXivに投稿されています²。ここでは重み$W$の正規化は行われていません。SphereFaceは文献^{3 4}で提案され、ICML'16とCVPR'17に通っています（ここの本質的な差分はよく分かりません）。SphereFaceでは重み$W$の正規化が行われていますが、特徴ベクトル$x$の正規化は行われていません。

ここからが面白いのですが、まず、CosFaceは何と文献^{5 6}で独立に提案されており、それぞれSignal Processing LettersとCVPR'18に通っています。これらの論文は、事前にarXivにも投稿されており、初版が投稿日が文献⁵は2018年1月17日、文献⁶は2018年1月29日となっています。そしてArcFaceの論文⁷は2018年1月23日にarXivに初版が投稿されています。

CosFaceは既にCosFaceという名前がついてしまっており、CosFaceという名前を冠し、CVPRに通っている文献⁶が有利かな、とか思っていましたが、何と文献^{5 6 7}の被引用数がちょうど56~57でほぼ同じでした。みんなちゃんと調べて全部引用しているのでしょうか。

他にも多数関連文献があるので、もう少し体系的に把握したい方は是非文献⁸の素晴らしいサーベイ論文を読みましょう。

※事実関係が間違っていたら教えてください！

（Center lossとかについてそのうち追記したい）

実装について

このPyTorch実装が良いです。
このレイヤを自分のモデルに差し込むだけで使えます。

Softmaxの温度パラメータについて

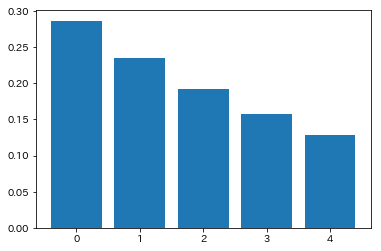
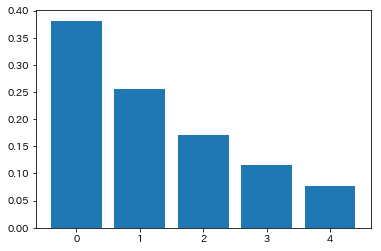
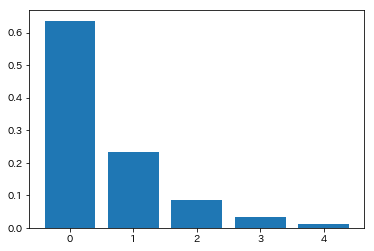
さて、今回logitsを$s$倍するという処理があり、softmaxの温度パラメータを制御していることと同等という話をしました。これがsoftmaxにどういう影響を与えるかを簡単に示します。
下記では$x = [1.0, 0.8, 0.6, 0.4, 0.2]^T$のベクトルを$s$倍してsoftmaxにかけた場合の出力値を図示しています。$s$が小さい場合（＝温度パラメータが大きい場合）には、本来softmaxが期待するmax関数の近似という役割をほとんど果たしておらず、$s$が大きくなるにつれ出力がmax関数に近づいていることが分かります。今回の手法ではlogitsの出力がコサインの値に制限され値が小さくなってしまうため、$s$によるスケーリングが必要となるという話でした。

$s=1$

$s=2$

$s=5$

$s=10$

1. もちろん、データベースに新たに個体が追加される度にモデルを学習し直すということは、理論的には可能。 ↩

2. R. Ranjan, C. Castillo, R, Chellappa, "L2-constrained Softmax Loss for Discriminative Face Verification," in arXiv:1703.09507, 2017. ↩ ↩²

3. W. Liu, Y. Wen, Z. Yu, and M. YangLarge-Margin, "Softmax Loss for Convolutional Neural Networks," in Proc. of ICML, 2016. ↩

4. W. Liu, Y. Wen, Z. Yu, M. Li, B. Raj, and L. Song, "SphereFace: Deep Hypersphere Embedding for Face Recognition," in Proc. of CVPR, 2017. ↩

5. F. Wang, W. Liu, H. Liu, and J. Cheng, "Additive Margin Softmax for Face Verification," in Signal Processing Letters, 2018. ↩ ↩² ↩³

6. H. Wang, Y. Wang, Z. Zhou, X. Ji, D. Gong, J. Zhou, Z. Li, and W. Liu, "CosFace: Large Margin Cosine Loss for Deep Face Recognition," in Proc. of CVPR, 2018. ↩ ↩² ↩³ ↩⁴

7. J. Deng, J. Guo, N. Xue, and S. Zafeiriou, "ArcFace: Additive Angular Margin Loss for Deep Face Recognition," in rXiv:1801.07698, 2018. ↩ ↩²

8. M. Wang and W. Deng, "Deep Face Recognition: A Survey," in arXiv:1804.06655, 2018. ↩