Introduction
In 1997, Hong Kong judge Wayne Gould saw a partly completed puzzle in a Japanese bookshop. Over six years, he developed a computer program to produce unique puzzles rapidly. The program tries to keep one puzzle ahead of you, by generating the next puzzle while you are solving the present one.
In the following we show a Prolog program, where the random generation of a Puzzle is performed in less than 2 seconds. The Prolog program was mainly developed for Dogelog Player. We could test the Prolog program also with Prolog systems such as SWI-Prolog, Scryer Prolog and Trealla Prolog.
Birthday Paradox
We recently posted about our approach how to solve Sudoku in that we related it to the map coloring problem. We also showed how to roll our own inequality graph library and not to depend on constraint solving libraries such as CLP(FD). This independence will pay off even more when we generate Sudoku puzzles.
Our basic idea is to modify the label/1 predicate of the solver, to randomly explore the solution space, and then use Prolog once/1 to pick the first accordingly generate Sudoku puzzle. This requires to generate the digits 1..9 in a random order. Here is a naive take:
indomain(X) :- between(1,9,_), random(R), X is 1+floor(R*9).
?- indomain(X), write(X), write(' '), fail.
7 5 3 1 5 6 4 2 6
The problem is related to the birthday paradox: Lets say we are invited to a party, how high is the probability that two people at that party have the same brithday. It turns out that the probability is quite high even for a small party. But how can we arrange our party of digits 1..9 randomly?
random_permutation(L, R) :-
add_random_keys(L, H),
keysort(H, J),
remove_keys(J, R).
add_random_keys([X|L], [K-X|R]) :- random(K), add_random_keys(L, R).
add_random_keys([], []).
remove_keys([_-X|L], [X|R]) :- remove_keys(L, R).
remove_keys([], []).
A popular method uses keysort/2 which is part if the Prolog ISO core standard. The corresponding code is shown above. This method avoids a quadratic effort and can therefor also be used to randomly permute larger lists. It is dominated by the complexity of the sorting algorithm, which is assumed to be O(N*log(N)).
Dynamic Heuristic
Before we start generating Sudoku puzzles we have to first improve our graph algorithm. So far our label/1 predicate used a Brute Force technique in that it just took the input inequality graph, and the labeling proceeded in the given input order. This fails for Markus Triskas example, and also for this example:
/* Ultimate Wiki 17 */
problem(7, [[_,_,_,_,_,_,_,1,_],
[4,_,_,_,_,_,_,_,_],
[_,2,_,_,_,_,_,_,_],
[_,_,_,_,5,_,4,_,7],
[_,_,8,_,_,_,3,_,_],
[_,_,1,_,9,_,_,_,_],
[3,_,_,4,_,_,2,_,_],
[_,5,_,1,_,_,_,_,_],
[_,_,_,8,_,6,_,_,_]]).
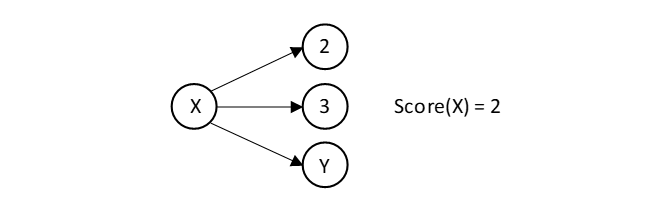
The label/1 predicate will even not finish after 1 minute. We therefore went on and implement a variable ordering heuristic. We opted for the smallest domain first (SDF) heuristic. As an ordering score we used the number of inequality edges that point to an instantiated node:
The higher the score the more values are excluded from the variable domain, and hence the smaller the domain is. Based on a predicate score/2 that computes the score from an adjacency list, one can derive a predicate best/4 that works like a predicate select/3 and that picks the best element. A heuristic label/1 predicate can then proceed as follows:
label([]) :- !.
label(L) :- best(L, K-S, _, R),
indomain(K), \+ (member(J,S), J==K),
label(R).
Static Heuristic
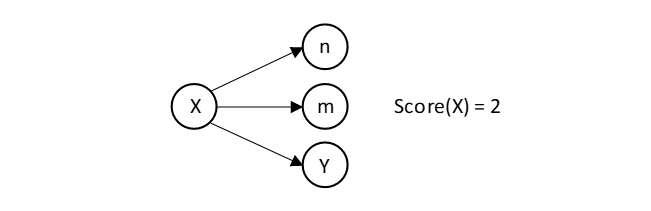
Armed with the new labeling device we can now solve all our problem samples below a minute. Unfortunately Markus Triskas example still needs 15 seconds in SWI-Prolog and so does another example, hence we didn't hit our goal of 2 second yet. Can we pull another rabbit out of the hat to improve the speed? As it turns out our scoring is agnostic to the values used in labeling:
We only compute the domain size approximately, for example if n and m get the same value the score is nevertheless 2. This plays in our hands and allows us to do the variable ordering once and forall before the search, and then use exactly this variable ordering for every backtracking:
label(L) :-
order(L, [], R),
search(R).
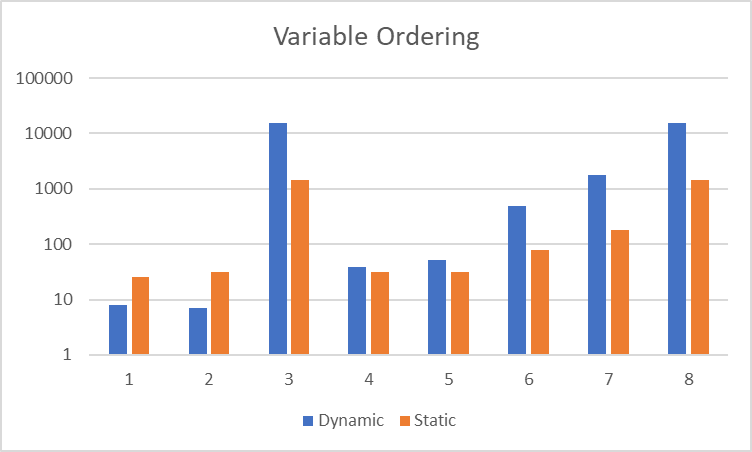
The below diagram shows our benchmark results on the problem suite. With static variable ordering we could solve our problem suite most of the time around 10-times faster. The benchmark results were obtained with SWI-Prolog 9.3.0, similar relative results were obtained with Dogelog Player 1.2.0, although Dogelog Player is absolutely seen slower than SWI-Prolog:
Random Labeling
We took the static variable ordering Sudoku solver as the baseline to produce a Sudoku generator. A Sudoku problem is then generated by feeding a blank Sudoku problem into the solver. Unfortunately static variable ordering suffers its first defeat in a blank Sudoku problem:
/* Blank */
problem(0, [[_,_,_,_,_,_,_,_,_],
[_,_,_,_,_,_,_,_,_],
[_,_,_,_,_,_,_,_,_],
[_,_,_,_,_,_,_,_,_],
[_,_,_,_,_,_,_,_,_],
[_,_,_,_,_,_,_,_,_],
[_,_,_,_,_,_,_,_,_],
[_,_,_,_,_,_,_,_,_],
[_,_,_,_,_,_,_,_,_]]).
It turns out that every cell and thus every Prolog variable gets trivially the same score zero, since no domain has yet been reduced. To mitigate this problem of a tie during static ordering we simply proceed as follows and random permutate the variables and their constraints before labeling:
label(L) :-
random_permutation(L, H),
order(H, [], R),
search(R).
The ordering itself takes its own toll of time. We measured for problem 1 and problem 2 around 31 ms for SWI-Prolog and around 100 ms for Dogelog Player for Java. This has to do with the fact that our ordering is naively implemented and has quadratic complexity. The Sudoku generator uses a further random source:
indomain(X) :-
random_permutation([1,2,3,4,5,6,7,8,9], L),
member(X, L).
The above assures that cells and thus Prolog variables are not always enumerated in the same sequence during labeling backtracking process. There is the danger that randomized algorithms show large time variation. Measurement showed that solving blank Sudokus didn't have that large a time variation and that it was around 1500 ms when using Dogelog Player for JavaScript.
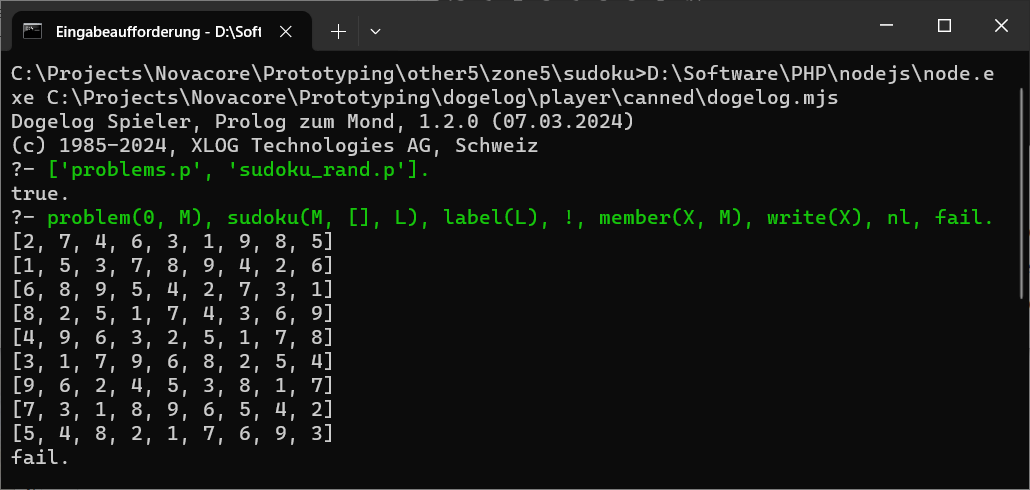
The above shows such a randomly generated Sudoku. We didn't get our head yet around how we will present them as a problem. Maybe easy, medium and hard Sudokus can be discriminated by the number of initially revealed cells and thus Prolog variables? Should we also check how determistic the promised solutions of the revealed cells are?
Conlusion
The smallest domain first variable ordering heuristic allowed us to solve some hard problems below a minute. Turning the heuristic into a static ordering before search gave us a further boost and the baseline for randomization. Measurement showed that solving blank Sudokus doesn't have a large time variation.
Map Coloring and Sudoku Solving
https://medium.com/@janburse_2989/map-coloring-and-sudoku-solving-4d3ca8e516b1
Toward Understanding Variable Ordering Heuristics
https://tidel.mie.utoronto.ca/pubs/promise.aics.pdf