数理最適化Advent Calender 2022の18日目の記事です。本記事は、9日目の記事「披露宴の席次を Gromov-Wasserstein 最適輸送で決めた話」で扱ったゲストの席次決めの問題を、13日目の記事「非線形な問題を線形な問題に変換する方法:真理値表を用いた1点排除のテクニック」の手法を使ってアプローチした結果を紹介します。本記事はAkira Tanimotoさんに特別な許可をいただいて執筆しています。感謝申し上げます。
1.はじめに
本記事を読む前にアドベントカレンダー9日目の披露宴の席次を Gromov-Wasserstein 最適輸送で決めた話、および13日目の記事「非線形な問題を線形な問題に変換する方法:真理値表を用いた1点排除のテクニック」を読んでもらえると幸いです。
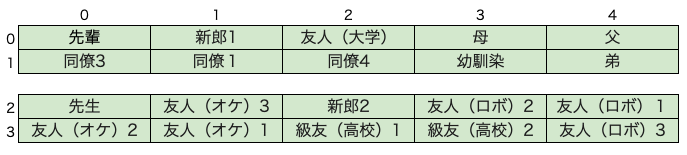
9日の記事では、結婚式の披露宴の席次決めの問題を解いており、ゲスト20人を20席に割り当てる問題です。再現用Colabの計算結果を参照すると、Gromov-Wasserstein 最適輸送問題を解いて得られた席次(以下、GW解(Gromov-Wasserstein)と呼ぶ)は、
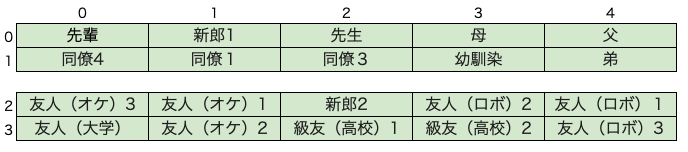
であり、GW解を初期解として貪欲法で得られた席次(以下、GR解(Greedy)と呼ぶ)は、
となるようです。
本記事では、上記の9日目の初期解を利用し、13日目の記事で紹介した手法を使って、席次決めに挑戦します。
2.席次決めの方法:数理最適化の厳密解法の部分適用
13日目の記事「非線形な問題を線形な問題に変換する方法:真理値表を用いた1点排除のテクニック」で触れましたが、ゲスト20人の席決めを厳密解法でバチッと解くのは困難であることを述べました。しかし、今回扱うデータは疎なデータであり、予備実験によりゲスト20人のうち10人ほど席を固定すると数秒で最適解を得られることがわかっています。そこで、上記で与えられた席次(初期解)に対して、10人の席を固定した上で最適化計算を行う方法を試してみます1。発想は単純で「とりあえず20人の席次を決めたのだけど、もしかしたらよりよい席次があるかもしれないから、その半分の10人を入れ替えて最適解を求めてみよう」というアイデアを実装しているだけです。具体的に次のステップを踏んで席次を求めます。
- ゲスト20人から席を固定する10人の組合せを列挙したものを「席固定プール」と呼ぶ。
- 「席固定プール」から20個ランダムに抽出して「席固定リスト」と呼ぶ。
- 「席固定リスト」のそれぞれについて、10人のゲストの席次(初期解)を固定して、数理最適化問題を解いて席次を求める。
「席固定プール」は184,756通りあるので、現実的な時間で全ての問題を解くのは難しいことに注意してください。また、「席固定リスト」の作成はランダム抽出を利用していますが、賢い抽出の方法はいくらでもありそうです。本問題の長机の構造を考慮すると、片方の10席を固定するなどのルールベースから、解の性質がばらけるように抽出するような理論的な方法もあります。
3.データの準備
データとして次のリストと辞書を利用します。
- ゲストのリスト:
G - ゲスト同士の親密度の辞書:
GG2R - 席のリスト:
S - 席同士の距離の辞書:
SS2D - GW解のリスト(要素はゲストと席のタプル):
FixGS_GW - 貪欲解のリスト(要素はゲストと席のタプル):
FixGS_GR
データはコードで次のように与えます。
G = ['新郎1', '新郎2', '幼馴染', '父', '母', '弟', '友人(オケ)1', '友人(オケ)2', '友人(オケ)3', '級友(高校)1', '級友(高校)2', '友人(ロボ)1', '友人(ロボ)2', '先輩', '友人(ロボ)3', '同僚1', '友人(大学)', '同僚3', '同僚4', '先生']
GG2R = {('新郎1', '先輩'): 2.0, ('新郎1', '同僚1'): 1.224744871391589, ('新郎1', '友人(大学)'): 1.0, ('新郎1', '同僚3'): 0.7071067811865476, ('新郎1', '同僚4'): 0.7071067811865476, ('新郎1', '先生'): 1.0, ('新郎2', '友人(オケ)1'): 1.0, ('新郎2', '友人(オケ)2'): 1.0, ('新郎2', '友人(オケ)3'): 1.0, ('新郎2', '級友(高校)1'): 1.7320508075688772, ('新郎2', '級友(高校)2'): 1.4142135623730951, ('新郎2', '友人(ロボ)1'): 1.0, ('新郎2', '友人(ロボ)2'): 1.0, ('新郎2', '友人(ロボ)3'): 1.0, ('幼馴染', '父'): 2.0, ('幼馴染', '母'): 2.0, ('幼馴染', '弟'): 2.0, ('父', '幼馴染'): 2.0, ('父', '母'): 2.0, ('父', '弟'): 2.0, ('母', '幼馴染'): 2.0, ('母', '父'): 2.0, ('母', '弟'): 2.0, ('弟', '幼馴染'): 2.0, ('弟', '父'): 2.0, ('弟', '母'): 2.0, ('友人(オケ)1', '新郎2'): 1.0, ('友人(オケ)1', '友人(オケ)2'): 1.0, ('友人(オケ)1', '友人(オケ)3'): 1.0, ('友人(オケ)1', '級友(高校)1'): 1.0, ('友人(オケ)2', '新郎2'): 1.0, ('友人(オケ)2', '友人(オケ)1'): 1.0, ('友人(オケ)2', '友人(オケ)3'): 1.0, ('友人(オケ)2', '級友(高校)1'): 1.0, ('友人(オケ)2', '友人(大学)'): 1.0, ('友人(オケ)3', '新郎2'): 1.0, ('友人(オケ)3', '友人(オケ)1'): 1.0, ('友人(オケ)3', '友人(オケ)2'): 1.0, ('友人(オケ)3', '級友(高校)1'): 1.0, ('友人(オケ)3', '友人(ロボ)2'): 1.0, ('級友(高校)1', '新郎2'): 1.7320508075688772, ('級友(高校)1', '友人(オケ)1'): 1.0, ('級友(高校)1', '友人(オケ)2'): 1.0, ('級友(高校)1', '友人(オケ)3'): 1.0, ('級友(高校)1', '級友(高校)2'): 1.4142135623730951, ('級友(高校)1', '友人(ロボ)1'): 1.0, ('級友(高校)1', '友人(ロボ)2'): 1.0, ('級友(高校)1', '友人(ロボ)3'): 1.0, ('級友(高校)1', '友人(大学)'): 1.0, ('級友(高校)2', '新郎2'): 1.4142135623730951, ('級友(高校)2', '級友(高校)1'): 1.4142135623730951, ('級友(高校)2', '友人(ロボ)1'): 1.0, ('級友(高校)2', '友人(ロボ)2'): 1.0, ('級友(高校)2', '友人(ロボ)3'): 1.0, ('友人(ロボ)1', '新郎2'): 1.0, ('友人(ロボ)1', '級友(高校)1'): 1.0, ('友人(ロボ)1', '級友(高校)2'): 1.0, ('友人(ロボ)1', '友人(ロボ)2'): 1.0, ('友人(ロボ)1', '友人(ロボ)3'): 1.0, ('友人(ロボ)2', '新郎2'): 1.0, ('友人(ロボ)2', '友人(オケ)3'): 1.0, ('友人(ロボ)2', '級友(高校)1'): 1.0, ('友人(ロボ)2', '級友(高校)2'): 1.0, ('友人(ロボ)2', '友人(ロボ)1'): 1.0, ('友人(ロボ)2', '友人(ロボ)3'): 1.0, ('先輩', '新郎1'): 2.0, ('先輩', '友人(ロボ)3'): 1.0, ('先輩', '同僚1'): 1.0, ('友人(ロボ)3', '新郎2'): 1.0, ('友人(ロボ)3', '級友(高校)1'): 1.0, ('友人(ロボ)3', '級友(高校)2'): 1.0, ('友人(ロボ)3', '友人(ロボ)1'): 1.0, ('友人(ロボ)3', '友人(ロボ)2'): 1.0, ('友人(ロボ)3', '先輩'): 1.0, ('同僚1', '新郎1'): 1.224744871391589, ('同僚1', '先輩'): 1.0, ('同僚1', '友人(大学)'): 1.0, ('同僚1', '同僚3'): 1.0, ('同僚1', '同僚4'): 1.0, ('友人(大学)', '新郎1'): 1.0, ('友人(大学)', '友人(オケ)2'): 1.0, ('友人(大学)', '級友(高校)1'): 1.0, ('友人(大学)', '同僚1'): 1.0, ('同僚3', '新郎1'): 0.7071067811865476, ('同僚3', '同僚1'): 1.0, ('同僚3', '同僚4'): 1.0, ('同僚4', '新郎1'): 0.7071067811865476, ('同僚4', '同僚1'): 1.0, ('同僚4', '同僚3'): 1.0, ('先生', '新郎1'): 1.0}
# 00 01 02 03 04
# 10 11 12 13 14
# 20 21 22 23 24
# 30 31 32 33 34
S = ['00', '01', '02', '03', '04', '10', '11', '12', '13', '14', '20', '21', '22', '23', '24', '30', '31', '32', '33', '34']
SS2D = {('00', '01'): 2.0, ('00', '02'): 1.0, ('00', '10'): 1.0, ('00', '11'): 1.0, ('01', '00'): 2.0, ('01', '02'): 2.0, ('01', '03'): 1.0, ('01', '10'): 1.0, ('01', '11'): 1.0, ('01', '12'): 1.0, ('02', '00'): 1.0, ('02', '01'): 2.0, ('02', '03'): 2.0, ('02', '04'): 1.0, ('02', '11'): 1.0, ('02', '12'): 1.0, ('02', '13'): 1.0, ('03', '01'): 1.0, ('03', '02'): 2.0, ('03', '04'): 2.0, ('03', '12'): 1.0, ('03', '13'): 1.0, ('03', '14'): 1.0, ('04', '02'): 1.0, ('04', '03'): 2.0, ('04', '13'): 1.0, ('04', '14'): 1.0, ('10', '00'): 1.0, ('10', '01'): 1.0, ('10', '11'): 2.0, ('10', '12'): 1.0, ('11', '00'): 1.0, ('11', '01'): 1.0, ('11', '02'): 1.0, ('11', '10'): 2.0, ('11', '12'): 2.0, ('11', '13'): 1.0, ('12', '01'): 1.0, ('12', '02'): 1.0, ('12', '03'): 1.0, ('12', '10'): 1.0, ('12', '11'): 2.0, ('12', '13'): 2.0, ('12', '14'): 1.0, ('13', '02'): 1.0, ('13', '03'): 1.0, ('13', '04'): 1.0, ('13', '11'): 1.0, ('13', '12'): 2.0, ('13', '14'): 2.0, ('14', '03'): 1.0, ('14', '04'): 1.0, ('14', '12'): 1.0, ('14', '13'): 2.0, ('20', '21'): 2.0, ('20', '22'): 1.0, ('20', '30'): 1.0, ('20', '31'): 1.0, ('21', '20'): 2.0, ('21', '22'): 2.0, ('21', '23'): 1.0, ('21', '30'): 1.0, ('21', '31'): 1.0, ('21', '32'): 1.0, ('22', '20'): 1.0, ('22', '21'): 2.0, ('22', '23'): 2.0, ('22', '24'): 1.0, ('22', '31'): 1.0, ('22', '32'): 1.0, ('22', '33'): 1.0, ('23', '21'): 1.0, ('23', '22'): 2.0, ('23', '24'): 2.0, ('23', '32'): 1.0, ('23', '33'): 1.0, ('23', '34'): 1.0, ('24', '22'): 1.0, ('24', '23'): 2.0, ('24', '33'): 1.0, ('24', '34'): 1.0, ('30', '20'): 1.0, ('30', '21'): 1.0, ('30', '31'): 2.0, ('30', '32'): 1.0, ('31', '20'): 1.0, ('31', '21'): 1.0, ('31', '22'): 1.0, ('31', '30'): 2.0, ('31', '32'): 2.0, ('31', '33'): 1.0, ('32', '21'): 1.0, ('32', '22'): 1.0, ('32', '23'): 1.0, ('32', '30'): 1.0, ('32', '31'): 2.0, ('32', '33'): 2.0, ('32', '34'): 1.0, ('33', '22'): 1.0, ('33', '23'): 1.0, ('33', '24'): 1.0, ('33', '31'): 1.0, ('33', '32'): 2.0, ('33', '34'): 2.0, ('34', '23'): 1.0, ('34', '24'): 1.0, ('34', '32'): 1.0, ('34', '33'): 2.0}
FixGS_GW = [('新郎1', '01'), ('新郎2', '33'), ('幼馴染', '13'), ('父', '12'), ('母', '03')
, ('弟', '02'), ('友人(オケ)1', '34'), ('友人(オケ)2', '30'), ('友人(オケ)3', '24'), ('級友(高校)1', '32')
, ('級友(高校)2', '23'), ('友人(ロボ)1', '31'), ('友人(ロボ)2', '21'), ('先輩', '00'), ('友人(ロボ)3', '22')
, ('同僚1', '11'), ('友人(大学)', '14'), ('同僚3', '20'), ('同僚4', '04'), ('先生', '10')]
FixGS_GR = [('新郎1', '01'), ('新郎2', '33'), ('幼馴染', '13'), ('父', '04'), ('母', '03')
, ('弟', '14'), ('友人(オケ)1', '34'), ('友人(オケ)2', '30'), ('友人(オケ)3', '31'), ('級友(高校)1', '32')
, ('級友(高校)2', '23'), ('友人(ロボ)1', '24'), ('友人(ロボ)2', '21'), ('先輩', '00'), ('友人(ロボ)3', '22')
, ('同僚1', '11'), ('友人(大学)', '02'), ('同僚3', '10'), ('同僚4', '12'), ('先生', '20')]
次に、GW解とGR解に対する「席固定プール」と「席固定リスト」を作成します。
- GW解席固定プール:
FixGSPool_GW - GW解席固定リスト:
FixGSPoolRand_GW - GR解席固定プール:
FixGSPool_GR - GR解席固定リスト:
FixGSPoolRand_GR
実際、次のコードでデータを作成します。
import itertools
import random
random.seed(1)
FixGSPool_GW = [tarFixGStp for tarFixGStp in itertools.combinations(FixGS_GW, 10)]
FixGSPoolRand_GW = random.sample(FixGSPool_GW, 20)
FixGSPool_GR = [tarFixGStp for tarFixGStp in itertools.combinations(FixGS_GR, 10)]
FixGSPoolRand_GR = random.sample(FixGSPool_GR, 20)
4.数理最適化モデルを解くためのクラスの定義
さて、探索をはじめる前に、数理最適化モデルを解くクラスGuests2Seatsを定義します。13日目の記事「非線形な問題を線形な問題に変換する方法:真理値表を用いた1点排除のテクニック」で紹介したクラスと同じものですが、show_seatsメソッドが追加されていることに注意していください。クラスGuests2Seatsは、コンストラクタで次のデータをセットします。
・G:ゲストの集合
・S:席の集合
・GG2R:ゲスト同士の親密度の辞書
・SS2D:席同士の距離の辞書
・FixGS:固定するゲストと席のタプルのリスト
また、次のメソッドを持ちます。
・modelingメソッド:数理最適化モデルの構築
・set_optionメソッド:最適化オプションの設定
・solveメソッド:最適化計算の実行
・show_resultsメソッド:結果の表示
・show_seatsメソッド:席次の表示
本記事では、次のコードは特に理解せずに読み進めることができます。気になる人は▶からコードを確認してください。
数理最適化モデルを解くためのクラス
import pulp
import time
class Guests2Seats:
def __init__(self, G, S, GG2R, SS2D, FixGS=[]):
# 入力データ
self.G = G
self.S = S
self.GG2R = GG2R
self.SS2D = SS2D
self.FixGS = FixGS
### モデリング用のリストを作成
# 変数 x 作成用
self.GS = [(g,s) for g in self.G for s in self.S]
# 変数 y 作成用
self.GSGS = [(g1,s1,g2,s2) for (g1,s1) in self.GS for (g2,s2) in self.GS if g1<g2]
# 目的関数定義用(非負の値のみ抽出)
self.GSGS_ = [(g1,s1,g2,s2) for (g1,s1,g2,s2) in self.GSGS if (g1,g2) in self.GG2R and (s1,s2) in self.SS2D]
# 最適化パラメータ
self.timeLimit = 360 # 計算時間[s]
self.msg = 1 # メッセージを(非)表示
self.model_type = 2
# 数理最適化モデルとソルバー
self.x = None
self.model = None
self.solver = None
# 最適化計算結果
self.status = None
self.elapsed_time = None
self.obj = None
self.resGS = None
self.G2G2FD = None
return
def modeling(self, model_type=2):
self.model_type = model_type
### 数理最適化モデルの定義
self.model = pulp.LpProblem('Guests2Seats', pulp.LpMaximize)
### 変数
self.x = pulp.LpVariable.dicts('x', self.GS, cat='Binary')
self.y = pulp.LpVariable.dicts('y', self.GSGS, cat='Binary')
### 制約
# 各ゲストは、1つの席に割り当てる
for g in self.G:
self.model += pulp.lpSum(self.x[g,s] for s in S) == 1
# 各席は、1つのゲストを割り当てられる
for s in self.S:
self.model += pulp.lpSum(self.x[g,s] for g in G) == 1
# ゲストの席への割当xと、2人のゲストの席への割当yの整合性をつける制約
if self.model_type == 2:
for g1,s1,g2,s2 in self.GSGS:
# 1点排除 ✕ 4
self.model += - self.x[g1,s1] - self.x[g2,s2] + self.y[g1,s1,g2,s2] <= 0
self.model += - self.x[g1,s1] + self.x[g2,s2] + self.y[g1,s1,g2,s2] <= 1
self.model += + self.x[g1,s1] - self.x[g2,s2] + self.y[g1,s1,g2,s2] <= 1
self.model += + self.x[g1,s1] + self.x[g2,s2] - self.y[g1,s1,g2,s2] <= 1
elif self.model_type == 3:
for g1,s1,g2,s2 in self.GSGS:
# 1点排除 & 3点排除
self.model += + self.x[g1,s1] + self.x[g2,s2] - self.y[g1,s1,g2,s2] <= 1
self.model += - self.x[g1,s1] - self.x[g2,s2] + 2 * self.y[g1,s1,g2,s2] <= 0
elif self.model_type == 4:
for g1,s1,g2,s2 in self.GSGS:
# 3点排除
self.model += - self.x[g1,s1] - self.x[g2,s2] + 2 * self.y[g1,s1,g2,s2] <= 0
elif self.model_type == 5:
for g1,s1,g2,s2 in self.GSGS:
self.model += self.y[g1,s1,g2,s2] <= self.x[g1,s1]
self.model += self.y[g1,s1,g2,s2] <= self.x[g2,s2]
elif self.model_type == 6:
for g1 in self.G:
for s1 in self.S:
for g2 in self.G:
if not g1<g2:continue
self.model += pulp.lpSum([self.y[g1,s1,g2,s2] for s2 in self.S]) <= self.x[g1,s1]
for g1 in self.G:
for s2 in self.S:
for g2 in self.G:
if not g1<g2:continue
self.model += pulp.lpSum([self.y[g1,s1,g2,s2] for s1 in self.S]) <= self.x[g2,s2]
elif self.model_type == 7:
for g1 in self.G:
for s1 in self.S:
for g2 in self.G:
if not g1<g2:continue
self.model += pulp.lpSum([self.y[g1,s1,g2,s2] for s2 in self.S]) <= self.x[g1,s1]
for g1 in self.G:
for s2 in self.S:
for g2 in self.G:
if not g1<g2:continue
self.model += pulp.lpSum([self.y[g1,s1,g2,s2] for s1 in self.S]) <= self.x[g2,s2]
for s1 in self.S:
for g1 in self.G:
for s2 in self.S:
self.model += pulp.lpSum([self.y[g1,s1,g2,s2] for g2 in self.G if g1<g2]) <= self.x[g1,s1]
for s1 in self.S:
for g2 in self.G:
for s2 in self.S:
self.model += pulp.lpSum([self.y[g1,s1,g2,s2] for g1 in self.G if g1<g2]) <= self.x[g2,s2]
# 予めゲストを特定の席に固定したい場合の制約
for g, s in self.FixGS:
self.model += self.x[g,s] == 1
### 目的関数:ゲスト同士の親密度が高く、席同士の距離が近いほどよい
self.model += pulp.lpSum(self.y[g1,s1,g2,s2] * self.GG2R[g1,g2] * self.SS2D[s1,s2] for g1,s1,g2,s2 in self.GSGS_)
return
def set_option(self, msg, timeLimit, solver='CBC'):
self.msg = msg
self.timeLimit = timeLimit
if solver == 'SCIP':
self.solver = pulp.SCIP(msg=self.msg, timeLimit=self.timeLimit)
else: # CBC
self.solver = pulp.PULP_CBC_CMD(msg=self.msg, timeLimit=self.timeLimit)
return
def solve(self):
start_time = time.time()
# 求解
self.status = self.model.solve(self.solver)
# 時間計測
self.elapsed_time = time.time() - start_time
# 最適化計算結果の整理
# ゲストの席への割当
self.resGS = [(g,s) for g in self.G for s in self.S if self.x[g,s].value()==1]
# 目的関数値の保存
self.obj = self.model.objective.value()
return
def show_result(self, x_flag=False):
if not self.status==1:return
print('=== Result ===')
print('status:', pulp.LpStatus[self.status])
print('obj:', self.obj)
print('elapsed_time:{:.2f}[s]'.format(self.elapsed_time))
if x_flag:
print('=== x ===')
for g, s in self.resGS:
print(g, '->', s)
return
def show_seats(self, split_n):
if not self.status==1:return
print('=== Seats ===')
resG = [g for g,s in sorted(self.resGS, key=lambda x:x[1])]
for i in range(0, len(resG), split_n):
Table = resG[i: i + split_n]
print(Table)
return
5.初期解であるGW解とGR解の確認
まず、GW解の目的関数を確認をするため、次のコードを実行します。
# GW解を初期解に、全員固定
g2s = Guests2Seats(G, S, GG2R, SS2D, FixGS_GW)
g2s.modeling(model_type=7)
g2s.set_option(msg=0, timeLimit=360)
g2s.solve()
g2s.show_result()
g2s.show_seats(5)
ゲスト全員を固定しているので、意味のない最適化計算を走らせていることに注意してください。標準出力として次が得られます。
=== Result ===
status: Optimal
obj: 48.517273611275535
elapsed_time:1.99[s]
=== Seats ===
['先輩', '新郎1', '弟', '母', '同僚4']
['先生', '同僚1', '父', '幼馴染', '友人(大学)']
['同僚3', '友人(ロボ)2', '友人(ロボ)3', '級友(高校)2', '友人(オケ)3']
['友人(オケ)2', '友人(ロボ)1', '級友(高校)1', '新郎2', '友人(オケ)1']
GW解の目的関数値は$48.51$であることがわかります。席次もGW解と一致していることが確認できます。
次にGR解の目的関数を確認をするため、次のコードを実行します。
# GR解を初期解に、全員固定
g2s = Guests2Seats(G, S, GG2R, SS2D, FixGS_GR)
g2s.modeling(model_type=7)
g2s.set_option(msg=0, timeLimit=360)
g2s.solve()
g2s.show_result()
g2s.show_seats(5)
こちらもゲスト全員を固定しているので、意味のない最適化計算を走らせていることに注意してください。標準出力として次が得られます。
=== Result ===
status: Optimal
obj: 59.93148717364862
elapsed_time:2.09[s]
=== Seats ===
['先輩', '新郎1', '友人(大学)', '母', '父']
['同僚3', '同僚1', '同僚4', '幼馴染', '弟']
['先生', '友人(ロボ)2', '友人(ロボ)3', '級友(高校)2', '友人(ロボ)1']
['友人(オケ)2', '友人(オケ)3', '級友(高校)1', '新郎2', '友人(オケ)1']
GR解の目的関数値は$59.93$であることがわかります。席次もGR解と一致していることが確認できます。
以上より、初期解の目的関数を確認できました。
| 解(席次) | 目的関数値 |
|---|---|
| GW解 | 48.51 |
| GR解 | 59.93 |
準備ができたので、最適化計算を進めます。
6.最適化計算
GW解を初期値に利用した場合
まず、GW解を初期値に、20個の要素をもつGW解席固定リストについて、最適化計算を実行します。
Result_GW = []
for i, tarFixGStp in enumerate(FixGSPoolRand_GW):
tarFixGS = list(tarFixGStp)
print('*** iteration:', i, '***')
g2s = Guests2Seats(G, S, GG2R, SS2D, tarFixGS)
g2s.modeling(model_type=7)
g2s.set_option(msg=0, timeLimit=3600)
g2s.solve()
g2s.show_result()
g2s.show_seats(5)
Result_GW.append(g2s)
print()
標準出力を省略しますが、実行結果を整理すると次の表が得られます。
| No. | 計算時間 | 目的関数値 | TOP3 |
|---|---|---|---|
| 0 | 2.16[s] | 54.22 | |
| 1 | 2.29[s] | 51.22 | |
| 2 | 2.25[s] | 54.22 | |
| 3 | 2.19[s] | 51.22 | |
| 4 | 2.22[s] | 54.22 | |
| 5 | 2.13[s] | 54.15 | |
| 6 | 2.31[s] | 52.51 | |
| 7 | 2.2[s] | 52.51 | |
| 8 | 2.09[s] | 51.51 | |
| 9 | 2.19[s] | 51.51 | |
| 10 | 3.42[s] | 57.32 | 1 |
| 11 | 2.22[s] | 52.93 | |
| 12 | 2.27[s] | 52.61 | |
| 13 | 2.55[s] | 54.19 | |
| 14 | 2.22[s] | 56.44 | 2 |
| 15 | 2.27[s] | 54.44 | |
| 16 | 2.06[s] | 54.63 | 3 |
| 17 | 2.96[s] | 52.51 | |
| 18 | 2.25[s] | 54.22 | |
| 19 | 3.85[s] | 50.51 |
目的関数値を確認すると、いずれもGW解の$48.51$よりも良さそうです。最大となったのはNo.10の目的関数値$57.32$ですが、GR解の目的関数値$59.93$には及びませんでした。悔しい!
GR解を初期値に利用した場合
GR解を初期値に、20個の要素をもつGR解席固定リストについて、最適化計算を実行します。
Result_GR = []
for i, tarFixGStp in enumerate(FixGSPoolRand_GR):
tarFixGS = list(tarFixGStp)
print('*** iteration:', i, '***')
g2s = Guests2Seats(G, S, GG2R, SS2D, tarFixGS)
g2s.modeling(modeling_type=7)
g2s.set_option(msg=0, timeLimit=3600)
g2s.solve()
g2s.show_result()
g2s.show_seats(5)
Result_GR.append(g2s)
print()
標準出力を省略しますが、実行結果を整理すると次の表が得られます。
| No. | 計算時間 | 目的関数値 | TOP3 |
|---|---|---|---|
| 0 | 3.91[s] | 62.61 | 1 |
| 1 | 2.01[s] | 61.19 | 2 |
| 2 | 2.08[s] | 59.93 | - |
| 3 | 2.0[s] | 59.93 | - |
| 4 | 2.21[s] | 61.19 | 2 |
| 5 | 2.12[s] | 59.93 | - |
| 6 | 1.97[s] | 59.93 | - |
| 7 | 1.99[s] | 59.93 | - |
| 8 | 2.1[s] | 59.93 | - |
| 9 | 2.26[s] | 60.93 | |
| 10 | 2.2[s] | 60.93 | |
| 11 | 2.26[s] | 60.93 | |
| 12 | 2.31[s] | 59.93 | - |
| 13 | 4.45[s] | 61.19 | 2 |
| 14 | 2.2[s] | 59.93 | - |
| 15 | 2.19[s] | 59.93 | - |
| 16 | 2.41[s] | 59.93 | - |
| 17 | 5.73[s] | 59.93 | - |
| 18 | 2.12[s] | 59.93 | - |
| 19 | 2.3[s] | 59.93 | - |
目的関数値を確認すると、最大となったのは、No.0で$125.22$でした。GR解の目的関数値$119.86$に対して、よい解が見つかりましたが、20個中13個では、GR解の目的関数値と一致しました。GR解の目的関数値もずいぶん良いことがわかります。
7.最適化計算2周目
上記で、GW解、およびGR解を初期解として、目的関数値が更新される解を得ることができました。
GW解を初期解とした最適解のNo.10を「GW解(改)」とし、GR解を初期解とした最適解No.0を「GR解(改)」とします。
次に、GW解(改)とGR解(改)に対する「席固定プール」と「席固定リスト」を作成します。
- GW解(改)席固定プール:
FixGSPool_GW2 - GW解(改)席固定リスト:
FixGSPoolRand_GW2 - GR解(改)席固定プール:
FixGSPool_GR2 - GR解(改)席固定リスト:
FixGSPoolRand_GR2
次のコードを実行します。
gw_g2s = Result_GW[10]
gr_g2s = Result_GR[0]
random.seed(1)
FixGSPool_GW2 = [tarFixGStp for tarFixGStp in itertools.combinations(gw_g2s.resGS, 10)]
FixGSPoolRand_GW2 = random.sample(FixGSPool_GW2, 20)
FixGSPool_GR2 = [tarFixGStp for tarFixGStp in itertools.combinations(gr_g2s.resGS, 10)]
FixGSPoolRand_GR2 = random.sample(FixGSPool_GR2, 20)
1行目、2行目で1周目の最適化結果を参照していることに注意してください。クラスを設計しておくと、インスタンスごと結果を保存しておけるので実験をするときに便利です。
GW解(改)を初期値に利用した場合
GW解(改)を初期値に、20個の要素をもつGR解(改)席固定リストについて、最適化計算を実行します。
Result_GW2 = []
for i, tarFixGStp in enumerate(FixGSPoolRand_GW2):
tarFixGS = list(tarFixGStp)
print('*** iteration:', i, '***')
g2s = Guests2Seats(G, S, GG2R, SS2D, tarFixGS)
g2s.modeling(model_type=7)
g2s.set_option(msg=0, timeLimit=3600)
g2s.solve()
g2s.show_result()
g2s.show_seats(5)
Result_GW2.append(g2s)
print()
標準出力を省略しますが、実行結果を整理すると次の表が得られます。
| No. | 計算時間 | 目的関数値 | TOP3 |
|---|---|---|---|
| 0 | 2.21[s] | 57.32 | - |
| 1 | 2.18[s] | 58.15 | |
| 2 | 2.18[s] | 58.15 | |
| 3 | 2.15[s] | 58.59 | |
| 4 | 2.16[s] | 60.86 | 2 |
| 5 | 2.18[s] | 58.15 | |
| 6 | 2.13[s] | 58.32 | |
| 7 | 2.01[s] | 61.13 | 1 |
| 8 | 2.03[s] | 57.32 | - |
| 9 | 2.07[s] | 57.32 | - |
| 10 | 3.27[s] | 57.32 | - |
| 11 | 2.3[s] | 58.15 | |
| 12 | 2.14[s] | 58.42 | |
| 13 | 2.16[s] | 58.42 | |
| 14 | 2.15[s] | 59.62 | |
| 15 | 2.01[s] | 57.32 | - |
| 16 | 2.05[s] | 58.63 | |
| 17 | 2.37[s] | 60.03 | 3 |
| 18 | 2.15[s] | 58.15 | |
| 19 | 2.0[s] | 57.32 | - |
目的関数値を確認すると、最大となったのは、No.7で$61.13$でした。辛うじてGR解の目的関数を超えることができました。
また、6個のGW解(改)の目的関数値に一致していることが確認できます。局所解に近いことを予感させます。
GR解(改)を初期値に利用した場合
| No. | 計算時間 | 目的関数値 | TOP3 |
|---|---|---|---|
| 0 | 3.73[s] | 62.61 | - |
| 1 | 2.08[s] | 62.61 | - |
| 2 | 2.04[s] | 62.61 | - |
| 3 | 2.04[s] | 63.61 | 1 |
| 4 | 2.02[s] | 62.61 | - |
| 5 | 2.04[s] | 62.61 | - |
| 6 | 1.98[s] | 62.61 | - |
| 7 | 1.98[s] | 62.61 | - |
| 8 | 1.96[s] | 62.61 | - |
| 9 | 2.35[s] | 63.61 | 1 |
| 10 | 2.12[s] | 62.61 | - |
| 11 | 2.08[s] | 63.61 | 1 |
| 12 | 2.04[s] | 62.61 | - |
| 13 | 4.17[s] | 62.61 | - |
| 14 | 2.08[s] | 62.61 | - |
| 15 | 2.08[s] | 62.61 | - |
| 16 | 2.17[s] | 62.61 | - |
| 17 | 2.9[s] | 62.61 | - |
| 18 | 2.01[s] | 62.61 | - |
| 19 | 2.06[s] | 62.61 | - |
目的関数値を確認すると、最大となったのは、No.3,9,11で$63.61$でした。また、20個中17個がGR解(改)の目的関数値と一致しました。こちらも局所解に近く、少しずつ収束していそうです。
8.おわりに
本記事は、数理最適化Advent Calender 2022の9日目の記事「披露宴の席次を Gromov-Wasserstein 最適輸送で決めた話」で扱ったゲストの席次決めの問題を、13日目の記事「非線形な問題を線形な問題に変換する方法:真理値表を用いた1点排除のテクニック」の手法を使ってアプローチした結果を紹介しました。13日目の記事で紹介した数理最適化の厳密解法を用いると、ゲスト20人に対して10人ほど席を固定すれば、数分の計算時間で最適解が得られます。そこで、GW解、およびGR解を初期解として、ゲスト20人のうち10人固定する組合せを20個ランダムに抽出して最適化計算を実行しました。さらに、1周目の最適化計算を用いて、2周目の最適化計算も実行しました。それぞれの結果は次の表に集約されます。
| 解(席次) | GW解ベースの目的関数値 | GR解ベースの目的関数値 |
|---|---|---|
| 初期解 | 48.51 | 59.93 |
| 1周目最適化結果 | 57.32 | 62.61 |
| 2周目最適化結果 | 61.13 | 63.61 |
本記事では、実験をここで打ち切りますが、2周目でも目的関数値が更新されている様子を見ると、やはりNP困難な問題であり、数多くの局所解が存在するのだろうなと想像できます。最適解にたどりつくのはかなり難しいようです。上記のアプローチは、$n$周目の最適化計算結果を利用して$n+1$周目の最適化計算を実行するように自然に実装を拡張して、自動化することができます。本記事では、十分に知見が得られたのでここで実験を打ち切りますが、この先にもいろいろ工夫の余地はありそうです。
最後に得られた席次をいくつか紹介します。
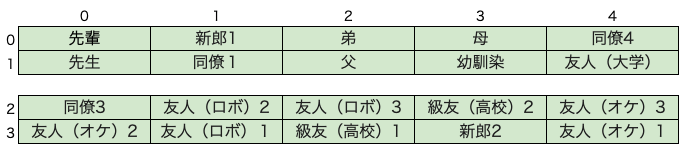
GR解を初期解とした最適化結果の席次
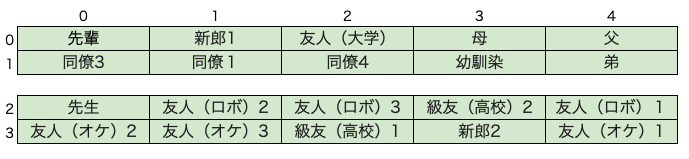
GR解(改)を初期解とした最適化結果の席次
「GR解(改)を初期解とした最適化結果」を観察すると、次のクラスタがまとまっているので、突拍子もない席次ではなさそうです。
- 母・父・弟
- 同僚4・同僚1・同僚3
- 友人(オケ)3・友人(オケ)1・友人(オケ)2
- 友人(ロボ)2・友人(ロボ)1・友人(ロボ)3
- 級友(高校)1・級友(高校)2
本記事で解いたのは、近似した数理最適化モデルなので、目的関数値が良ければよいという話ではないのですが、上記で紹介した席次以外にも計算過程で良質な目的関数値の解(席次)がたくさん得られています。その中にはきっと現実的に気に入ってもらえる席次もあればよいなと思っています。実際のところは、新郎新婦、ゲストのみなさんに聞かないとわからなそうです。
全体的な感想ですが、各ゲストに対する親密度の下限値制約を設けたり、グループごとに領域を決める制約なども考えられそうです。また、最適化計算は重要ですが「ゲスト同士の親密度」と「席同士の距離」の定義の仕方が最適解にとって支配的なので、この定義方法について議論するのも面白そうです2。
元々、この問題を解きたいと思ったきっかけは、席次決めの問題が「小学校、中学校、高等学校の席替え問題」と類似しているためです。時間ができたら解いてみようと思っていたので、ちょうどよい機会になりました。本記事を教員の方が閲覧していましたら是非、学校で試してみてください。3つくらい座席表を作成して「AI3で席を決めました!みなさん、投票して選んでください!」と言えばHRが盛り上がりそうです。
最後に宣伝となりますが、数理最適化コミュニティCasual Optimizationの運営のお手伝いをしております。イベントOptimization Nightや雑談形式のopt-radio、そして輪読会であるopt-readなども開催しています。興味をお持ちの方がいましたらリンク先からslackへの参加ができます。今回、ゲストの席次決め問題に挑戦しましたが、コミュニティのハッカソンなどでみんなでワイワイガヤガヤしても良さそうですね。ハッカソン中に新郎新婦の要望で要件が変わるとかあると盛り上がりそう。。。