数理最適化Advent Calender 2022の13日目の記事です。本記事は、9日目の記事「披露宴の席次を Gromov-Wasserstein 最適輸送で決めた話」を読んだことをきっかけに執筆しました。Akira Tanimotoさんに感謝申し上げます。
1.はじめに
本記事を読む前にアドベントカレンダー9日目の披露宴の席次を Gromov-Wasserstein 最適輸送で決めた話を読んでもらえると幸いです。9日の記事では、結婚式の披露宴の席次決めの問題を解いており、ゲスト20人を20席に割り当てる問題です。再現用Colabの計算結果を参照すると次のような席次がアウトプットとして得られるようです。
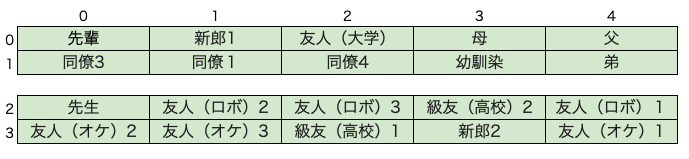
長机に家族や友人などのゲストを割り当てる問題のようです。私も結婚式に招待されると、正面、隣、斜めなどに身近な人間が座ってるかどうか、ドキドキしながら披露宴会場に向かった記憶があります。
この問題について9日の記事で、「知り合い同士を近くに配席する」問題は非凸な二次計画になり汎用ソルバでうまく解けないという記述がありました。確かに、自然に定式化すると目的関数が非線形(変数同士の掛け算)となりそのままではソルバー1は受け付けてくれないのですが、目的関数の非線形部分を線形に表現するテクニック(真理値表を用いた1点排除のテクニック)を用いて、汎用ソルバーが解ける形に変形させることができることを紹介します。ただし、誤解しないでほしいのが「汎用ソルバーに解ける形で表現できる」ことと「汎用ソルバーで現実的な時間で解ける」ことは別の話で、超小規模な問題しか解けないことに注意してください。実際、ゲスト20人の席決めですらフリーソルバーでは最適解を求めることはできません。しかしながら、20人程度の問題であれば工夫次第で最適解に近い解を見つけることはできます。その方法については18日のアドベントカレンダーで紹介します。
本記事を読むことで次の知識が身につきます。
- 非線形な問題を線形に表現することで汎用ソルバーに解ける形で表現できることがある
- 真理値表を用いた1点排除のテクニック
- 複数点排除のテクニック(拡張)
- 数理最適化モデルとソルバーの相性
また、以下では数理最適化プログラムをクラスを利用して実装します。数理最適化プログラムのクラス化に慣れていない方は、アドベントカレンダー10日目のPythonではじめる数理最適化:クラス設計入門から読み始めると理解しやすいかもしれません。
2.数理最適化モデル
まずは、数理最適化モデルを定義します。まず、目的関数が非線形となる自然な形にモデリングします。
①数理最適化モデル(目的関数:非線形)
-
集合
- ゲストの集合:$G$
- 席の集合:$S$
-
定数
- ゲスト同士の親密度:$r_{g1,g2}\ \ (g1, g2\in G)$
- 席同士の距離:$s_{s1,s2}\ \ (s1, s2\in S)$
-
変数
- ゲストの席の割り当て:$x_{g,s} \in \{0,1\}\ \ (g\in G, s \in S)$
-
制約式
- 各ゲストは、1つの席に割り当てる:
$\sum_{s \in S}x_{g,s} = 1\ \ (\forall g\in G)$ - 各席は、1人のゲストを割り当てられる:
$\sum_{g \in G}x_{g,s} = 1\ \ (\forall s\in S)$
- 各ゲストは、1つの席に割り当てる:
-
目的関数(最大化)
ゲスト同士の親密度が高く、席同士の距離が近いほどよい:
$\sum_{g1,g2 \in G, g1<g2, s1,s2 \in S}x_{g1,s1}\cdot x_{g2,s2}\cdot r_{g1,g2}\cdot d_{s1,s2}$
目的関数を確認してください。$x_{g1,s1}\cdot x_{g2,s2}$は論理積を表しており、「ゲスト$g1$が席$s1$に割り当てられ」かつ「ゲスト$g2$が席$s2$に割り当てられる」場合を表しており、そのときに限り親密度$r_{g1,g2}$と距離(近いほど大きい)$d_{s1,s2}$の積を目的関数値に反映させるという式です。一般的に自然な定式化をした場合に論理積が現れ、目的関数が非線形になってしまうことがあります。
そこで、真理値表を用いた1点排除のテクニックを使って、次のように線形となる形にモデリングします。
追記:以下の数理最適化モデル②〜⑦はohtamanさん、から「変数$y$について対称性を考えると変数の数を半分にできる」という指摘を受けて修正をしました2。
②数理最適化モデル(目的関数:線形/1点排除)
-
集合
- ゲストの集合:$G$
- 席の集合:$S$
-
定数
- ゲスト同士の親密度:$r_{g1,g2}\ \ (g1, g2\in G)$
- 席同士の距離:$s_{s1,s2}\ \ (s1, s2\in S)$
-
変数
- ゲストの席の割り当て:$x_{g,s} \in \{0,1\}\ \ (g\in G, s \in S)$
- ゲストの席の割り当ての組合せ:$y_{g1,s1,g2,s2} \in \{0,1\}\ \ (g1,g2\in G, g1<g2,s1,s2 \in S)$
-
制約式
- 各ゲストは、1つの席に割り当てる:
$\sum_{s \in S}x_{g,s} = 1\ \ (\forall g\in G)$ - 各席は、1つのゲストを割り当てられる:
$\sum_{g \in G}x_{g,s} = 1\ \ (\forall s\in S)$ - 変数$x$と変数$y$の整合性$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})$の制約
- $(0,0,1)$を排除する制約
$- x_{g1,s1} - x_{g2,s2} + y_{g1,s1,g2,s2} \leq 0 \ \ (\forall g1,g2\in G, g1<g2, \forall s1,s2 \in S)$ - $(0,1,1)$を排除する制約
$- x_{g1,s1} + x_{g2,s2} + y_{g1,s1,g2,s2} \leq 1 \ \ (\forall g1,g2\in G, g1<g2, \forall s1,s2 \in S)$ - $(1,0,1)$を排除する制約
$+ x_{g1,s1} - x_{g2,s2} + y_{g1,s1,g2,s2} \leq 1 \ \ (\forall g1,g2\in G, g1<g2, \forall s1,s2 \in S)$ - $(1,1,0)$を排除する制約
$+ x_{g1,s1} + x_{g2,s2} - y_{g1,s1,g2,s2} \leq 1 \ \ (\forall g1,g2\in G, g1<g2, \forall s1,s2 \in S)$
- $(0,0,1)$を排除する制約
- 各ゲストは、1つの席に割り当てる:
-
目的関数(最大化)
ゲスト同士の親密度が高く、席同士の距離が近いほどよい:
$\sum_{g1,g2 \in G, g1<g2, s1,s2 \in S}y_{g1,s1,g2,s2}\cdot r_{g1,g2}\cdot d_{s1,s2}$
上記の数理モデルの変化を確認してみましょう。まず、変数として、ゲストの席の割り当ての組合せとして
$$y_{g1,s1,g2,s2} \in \{0,1\}\ \ (g1,g2\in G, g1<g2, s1,s2 \in S)$$
を用意しました。必要なゲストの席の割り当ての組合せが得られれば、目的関数を
$$\sum_{g1,g2 \in G, g1<g2, s1,s2 \in S}y_{g1,s1,g2,s2}\cdot r_{g1,g2}\cdot d_{s1,s2}$$
と書けるようになるので、線形な目的関数に書き換えられることに気づきます。問題は、変数$x$と変数$y$の整合性をつける点です。「変数$x$と変数$y$の整合性$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})$の制約」で4点の排除を行っていますが、これは何を意味しているのでしょうか。この式は3つの変数$x_{g1,s1}$、$x_{g2,s2}$、$y_{g1,s1,g2,s2}$の真理値表から$x$と$y$の整合性がつくような$\{0,1\}$への写像を作成することで導出できます3。次に、真理値表から$\{0,1\}$への写像をあらわす表を作成しました。ただし、「$0/1$」のカラムは変数$x$と変数$y$の整合性を考慮して$0$か$1$が入るか考える必要があります。
| $x_{g1,s1}$ | $x_{g2,s2}$ | $y_{g1,s1,g2,s2}$ | 0/1 |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
例えば、$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})=(1,1,1)$のとき、「ゲスト$g1$が席$s1$に割り当てられ」かつ「ゲスト$g2$が席$s2$に割り当てられる」場合なので、このとき$y_{g1,s1,g2,s2}=1$となれば、親密度$r_{g1,g2}$と距離$d_{s1,s2}$の積を目的関数値に反映することができます。この組合わせは必要なのでカラム「0/1」に$1$を指定します。
次に、排除する組合わせも考えます。例えば、$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})=(1,1,0)$のとき、「ゲスト$g1$が席$s1$に割り当てられ」かつ「ゲスト$g2$が席$s2$に割り当てられている」場合なので、このときに$y_{g1,s1,g2,s2}=0$となると親密度$r_{g1,g2}$と距離$d_{s1,s2}$の積を目的関数値に反映できません。この組合わせは必要ないのでカラム「0/1」に$0$を指定します。
このようにして、$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})$の全ての組合せに対して、必要な場合は$1$、排除したい場合は$0$をカラム「0/1」に指定します。
さて、真理値表から$\{0,1\}$への写像を作成しましたが、どのように制約を作成するのでしょうか。大事なのはカラム「$0$/$1$」が$1$となる組合わせは気にする必要はなく、カラム「$0$/$1$」が$0$となる組合わせだけを排除すればよいということです。そこで、1点排除のテクニックを利用すれば機械的に制約式を作成できます。例えば、
$$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})=(1,1,0)$$
の組合せを排除する式は
$$a \cdot x_{g1,s1} + b \cdot x_{g2,s2} + c \cdot y_{g1,s1,g2,s2} \leq d$$
と書けますが、$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})=(1,1,0)$となる場合にのみ左辺が最大値をとるように係数$a$、$b$、$c$をとれば、その最大値だけを排除するように$d$を決めることができます。例えば、真理値表の値が$0$の場合は係数を$-1$に、真理値表の値が$1$の場合は係数を$1$とすると、$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})=(1,1,0)$のときのみ左辺値が最大値をとるので、その最大値を排除するように右辺の値を定めれば、
$$1 \cdot x_{g1,s1} + 1 \cdot x_{g2,s2} + (-1) \cdot y_{g1,s1,g2,s2} \leq 1$$
という式が得られます。機械的に作成した式でピンとこなくても幾何的に考えれば直感的にわかります。真理値表の1つの組合せを排除することは、3次元上の長さ$1$の立方体の頂点の1点を排除する平面の式(切除平面)を求めていることと同じになります(以下の図の軸の名前は簡略化しています)。
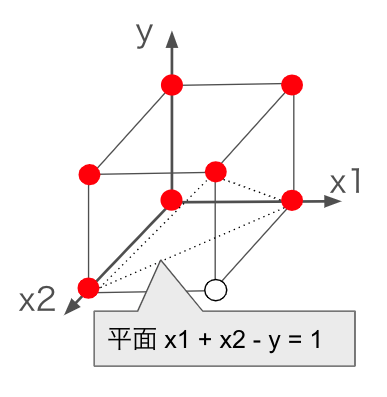
最後に、ソルバーで解く前にもう1つ工夫をします。$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})$=$(0,0,1),(0,1,1),(1,0,1),(1,1,0)$の4点を排除する制約はかなり複雑です。このような制約はソルバーに負担をかけ、計算速度が遅くなります。そこで1点排除を拡張して2点排除、3点排除はできないか検討します。改めて3次元空間の立方体の頂点で排除したい4点を図示します。
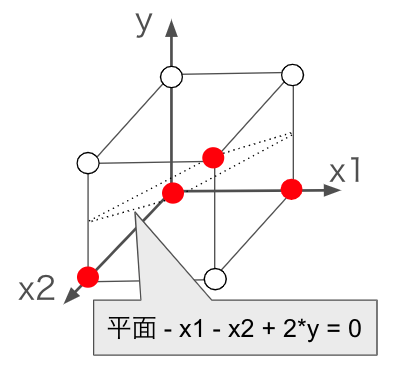
すると、上部の3点$(0,0,1),(0,1,1),(1,0,1)$をまとめて排除するような平面がとれそうだと気づきます。実際、$(0,0,0),(1,1,1)$を通る平面を求めることで、式
$$- x_{g1,s1} - x_{g2,s2} + 2 \cdot y_{g1,s1,g2,s2} \leq 0$$
を得ることができます4。このようにして複数点排除をすることで次の数理最適化モデルが出来上がります。
③数理最適化モデル(目的関数:線形/1点排除&3点排除)
-
集合
- ゲストの集合:$G$
- 席の集合:$S$
-
定数
- ゲスト同士の親密度:$r_{g1,g2}\ \ (g1, g2\in G)$
- 席同士の距離:$s_{s1,s2}\ \ (s1, s2\in S)$
-
変数
- ゲストの席の割り当て:$x_{g,s} \in \{0,1\}\ \ (g\in G, s \in S)$
- ゲストの席の割り当ての組合せ:$y_{g1,s1,g2,s2} \in \{0,1\}\ \ (g1,g2\in G, g1<g2, s1,s2 \in S)$
-
制約式
- 各ゲストは、1つの席に割り当てる:
$\sum_{s \in S}x_{g,s} = 1\ \ (\forall g\in G)$ - 各席は、1つのゲストを割り当てられる:
$\sum_{g \in G}x_{g,s} = 1\ \ (\forall s\in S)$ - 変数$x$と変数$y$の整合性$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})$の制約
- $(1,1,0)$を排除する制約
$+ x_{g1,s1} + x_{g2,s2} - y_{g1,s1,g2,s2} \leq 1 \ \ (\forall g1,g2\in G, g1<g2, \forall s1,s2 \in S)$ - $(0,0,1),(0,1,1),(1,0,1)$の3点を排除する制約
$- x_{g1,s1} - x_{g2,s2} + 2\cdot y_{g1,s1,g2,s2} \leq 0 \ \ (\forall g1,g2\in G, g1<g2, \forall s1,s2 \in S)$
- $(1,1,0)$を排除する制約
- 各ゲストは、1つの席に割り当てる:
-
目的関数(最大化)
ゲスト同士の親密度が高く、席同士の距離が近いほどよい:
$\sum_{g1,g2 \in G, g1<g2, s1,s2 \in S}y_{g1,s1,g2,s2}\cdot r_{g1,g2}\cdot d_{s1,s2}$
すっきりしました。ここでは1点排除のテクニックを紹介しましたが、上記のテクニックを使えば、任意の真理値表から$\{0,1\}$への写像に対して、同値となる複数の線形な不等式が存在することを導けます5。
追記:以下、④⑤の数理最適化モデルは2022年12月20日に今井義弥氏から「yの最大化の仮定を使うことでより数理最適化モデルをシンプルにできる」という指摘を受けて追記しました。
③では真理値表だけに注目して制約を組み立てましたが、さらに目的関数の最大化の仮定を使うと制約
$$+ x_{g1,s1} + x_{g2,s2} - y_{g1,s1,g2,s2} \leq 1 \ \ (\forall g1,g2\in G, g1<g2, \forall s1,s2 \in S)$$
が不要となります。真理値表の
| $x_{g1,s1}$ | $x_{g2,s2}$ | $y_{g1,s1,g2,s2}$ | 0/1 |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
の組合せに注目すると、変数$y$を最大化する場合、真理値表を
| $x_{g1,s1}$ | $x_{g2,s2}$ | $y_{g1,s1,g2,s2}$ | 0/1 |
|---|---|---|---|
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
と解釈してもよいからです。なぜならば、$x_{g1,s1}=1$かつ$x_{g2,s2}=1$の場合、後者の真理値表では$y_{g1,s1,g2,s2}=0$も$y_{g1,s1,g2,s2}=1$も実行可能解となりますが、目的関数を最大化する解では、$y_{g1,s1,g2,s2}$を最大化させるため$y_{g1,s1,g2,s2}=0$をとることは起きないためです。すなわち、$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})=(1,1,0)$は変数$y$の最大化により自動で排除できます。次の数理最適化モデルが得られます。
④数理最適化モデル(目的関数:線形/3点排除/y最大化)
-
集合
- ゲストの集合:$G$
- 席の集合:$S$
-
定数
- ゲスト同士の親密度:$r_{g1,g2}\ \ (g1, g2\in G)$
- 席同士の距離:$s_{s1,s2}\ \ (s1, s2\in S)$
-
変数
- ゲストの席の割り当て:$x_{g,s} \in \{0,1\}\ \ (g\in G, s \in S)$
- ゲストの席の割り当ての組合せ:$y_{g1,s1,g2,s2} \in \{0,1\}\ \ (g1,g2\in G, g1<g2, s1,s2 \in S)$
-
制約式
- 各ゲストは、1つの席に割り当てる:
$\sum_{s \in S}x_{g,s} = 1\ \ (\forall g\in G)$ - 各席は、1つのゲストを割り当てられる:
$\sum_{g \in G}x_{g,s} = 1\ \ (\forall s\in S)$ - 変数$x$と変数$y$の整合性$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})$の制約
- $(0,0,1),(0,1,1),(1,0,1)$の3点を排除する制約
$- x_{g1,s1} - x_{g2,s2} + 2\cdot y_{g1,s1,g2,s2} \leq 0 \ \ (\forall g1,g2\in G, g1<g2, \forall s1,s2 \in S)$
- $(0,0,1),(0,1,1),(1,0,1)$の3点を排除する制約
- 各ゲストは、1つの席に割り当てる:
-
目的関数(最大化)
ゲスト同士の親密度が高く、席同士の距離が近いほどよい:
$\sum_{g1,g2 \in G, g1<g2, s1,s2 \in S}y_{g1,s1,g2,s2}\cdot r_{g1,g2}\cdot d_{s1,s2}$
次に、今井氏から別途提案いただいた数理最適化モデルを紹介します6。③の数理最適化モデルでは3点排除の制約式を1本用いて3点を排除しました。ここでは、2点排除の制約式を2本用いて3点を排除することを考えます(1点は重複して排除)。つまり、$(0,0,1),(0,1,1)$の2点を排除する制約として
$$y_{g1,s1,g2,s2} \leq x_{g1,s1} \ \ (\forall g1,g2\in G, g1<g2, \forall s1,s2 \in S)$$
を得ることができます。一方、$(0,0,1),(1,0,1)$の2点を排除する制約として
$$y_{g1,s1,g2,s2} \leq x_{g2,s2} \ \ (\forall g1,g2\in G, g1<g2, \forall s1,s2 \in S)$$
を得ることができます。このとき、$(0,0,1)$が重複して排除されていることに注意してください。次の数理最適化モデルが得られます。
⑤数理最適化モデル(目的関数:線形/2点排除✕2/y最大化)
-
集合
- ゲストの集合:$G$
- 席の集合:$S$
-
定数
- ゲスト同士の親密度:$r_{g1,g2}\ \ (g1, g2\in G)$
- 席同士の距離:$s_{s1,s2}\ \ (s1, s2\in S)$
-
変数
- ゲストの席の割り当て:$x_{g,s} \in \{0,1\}\ \ (g\in G, s \in S)$
- ゲストの席の割り当ての組合せ:$y_{g1,s1,g2,s2} \in \{0,1\}\ \ (g1,g2\in G, g1<g2, s1,s2 \in S)$
-
制約式
- 各ゲストは、1つの席に割り当てる:
$\sum_{s \in S}x_{g,s} = 1\ \ (\forall g\in G)$ - 各席は、1つのゲストを割り当てられる:
$\sum_{g \in G}x_{g,s} = 1\ \ (\forall s\in S)$ - 変数$x$と変数$y$の整合性$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})$の制約
- $(0,0,1),(0,1,1)$の2点を排除する制約
$y_{g1,s1,g2,s2} \leq x_{g1,s1} \ \ (\forall g1,g2\in G, g1<g2, \forall s1,s2 \in S)$ - $(0,0,1),(1,0,1)$の2点を排除する制約
$y_{g1,s1,g2,s2} \leq x_{g2,s2} \ \ (\forall g1,g2\in G, g1<g2, \forall s1,s2 \in S)$
- $(0,0,1),(0,1,1)$の2点を排除する制約
- 各ゲストは、1つの席に割り当てる:
-
目的関数(最大化)
ゲスト同士の親密度が高く、席同士の距離が近いほどよい:
$\sum_{g1,g2 \in G, g1<g2, s1,s2 \in S}y_{g1,s1,g2,s2}\cdot r_{g1,g2}\cdot d_{s1,s2}$
追記:以下、⑥の数理最適化モデルは2022年12月21日に今井義弥氏から「任意の$g1,s1,g2$に対して、$y_{g1,s2,g2,s2}=1$となる$s2$が高々1つしか存在しないという仮定を使うことでより数理最適化モデルをよりシンプルにできる方法を思いついた。」という連絡を受けて追記しました7。
⑤の数理最適化モデルの2点排除の制約式について、「任意の$g1,s1,g2$に対して$y_{g1,s2,g2,s2}=1$となる$s2$が高々1つしか存在しない」という仮定を用いると
$$\sum_{s2\in S}y_{g1,s1,g2,s2} \leq x_{g1,s1} \ \ (\forall g1,g2\in G, g1<g2, \forall s1 \in S)$$
を得ることができます。一方、「任意の$g1,s2,g2$に対して$y_{g1,s2,g2,s2}=1$となる$s1$が高々1つしか存在しない」という仮定を用いると
$$\sum_{s1\in S}y_{g1,s1,g2,s2} \leq x_{g2,s2} \ \ (\forall g1,g2\in G, g1<g2, \forall s2 \in S)$$
を得ることができます。和をとることで制約式の数が激的に減ることがわかります。
⑥数理最適化モデル(目的関数:線形/2点排除✕2/y最大化/和の利用:S)
-
集合
- ゲストの集合:$G$
- 席の集合:$S$
-
定数
- ゲスト同士の親密度:$r_{g1,g2}\ \ (g1, g2\in G)$
- 席同士の距離:$s_{s1,s2}\ \ (s1, s2\in S)$
-
変数
- ゲストの席の割り当て:$x_{g,s} \in \{0,1\}\ \ (g\in G, s \in S)$
- ゲストの席の割り当ての組合せ:$y_{g1,s1,g2,s2} \in \{0,1\}\ \ (g1,g2\in G, g1<g2, s1,s2 \in S)$
-
制約式
- 各ゲストは、1つの席に割り当てる:
$\sum_{s \in S}x_{g,s} = 1\ \ (\forall g\in G)$ - 各席は、1つのゲストを割り当てられる:
$\sum_{g \in G}x_{g,s} = 1\ \ (\forall s\in S)$ - 変数$x$と変数$y$の整合性$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})$の制約
- $(0,0,1),(0,1,1)$の2点を排除する制約&和の利用
$\sum_{s2\in S}y_{g1,s1,g2,s2} \leq x_{g1,s1} \ \ (\forall g1,g2\in G, g1<g2, \forall s1 \in S)$ - $(0,0,1),(1,0,1)$の2点を排除する制約&和の利用
$\sum_{s1\in S}y_{g1,s1,g2,s2} \leq x_{g2,s2} \ \ (\forall g1,g2\in G, g1<g2, \forall s2 \in S)$
- $(0,0,1),(0,1,1)$の2点を排除する制約&和の利用
- 各ゲストは、1つの席に割り当てる:
-
目的関数(最大化)
ゲスト同士の親密度が高く、席同士の距離が近いほどよい:
$\sum_{g1,g2 \in G, g1<g2, s1,s2 \in S}y_{g1,s1,g2,s2}\cdot r_{g1,g2}\cdot d_{s1,s2}$
追記(2022年12月28日):今井氏から追加で提案された⑥に冗長な制約を追加する⑦の数理最適化モデルを紹介します。
⑥では集合$S$について和をとる制約に変更しましたが、さらに集合$G$について和をとる制約を追加します。説明は省略します。
⑦数理最適化モデル(目的関数:線形/2点排除✕2/y最大化/和の利用:S&G)
-
集合
- ゲストの集合:$G$
- 席の集合:$S$
-
定数
- ゲスト同士の親密度:$r_{g1,g2}\ \ (g1, g2\in G)$
- 席同士の距離:$s_{s1,s2}\ \ (s1, s2\in S)$
-
変数
- ゲストの席の割り当て:$x_{g,s} \in \{0,1\}\ \ (g\in G, s \in S)$
- ゲストの席の割り当ての組合せ:$y_{g1,s1,g2,s2} \in \{0,1\}\ \ (g1,g2\in G, g1<g2, s1,s2 \in S)$
-
制約式
- 各ゲストは、1つの席に割り当てる:
$\sum_{s \in S}x_{g,s} = 1\ \ (\forall g\in G)$ - 各席は、1つのゲストを割り当てられる:
$\sum_{g \in G}x_{g,s} = 1\ \ (\forall s\in S)$ - 変数$x$と変数$y$の整合性$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})$の制約
-
$(0,0,1),(0,1,1)$の2点を排除する制約&和の利用
$\sum_{s2\in S}y_{g1,s1,g2,s2} \leq x_{g1,s1} \ \ (\forall g1,g2\in G, g1<g2, \forall s1 \in S)$
$\sum_{g2\in G,, g1<g2}y_{g1,s1,g2,s2} \leq x_{g1,s1} \ \ (\forall g1\in G, \forall s1,s2 \in S)$ -
$(0,0,1),(1,0,1)$の2点を排除する制約&和の利用
$\sum_{s1\in S}y_{g1,s1,g2,s2} \leq x_{g2,s2} \ \ (\forall g1,g2\in G, g1<g2, \forall s2 \in S)$
$\sum_{g1\in G, g1<g2}y_{g1,s1,g2,s2} \leq x_{g2,s2} \ \ (\forall g2\in G, \forall s1,s2 \in S)$
-
- 各ゲストは、1つの席に割り当てる:
-
目的関数(最大化)
ゲスト同士の親密度が高く、席同士の距離が近いほどよい:
$\sum_{g1,g2 \in G, g1<g2, s1,s2 \in S}y_{g1,s1,g2,s2}\cdot r_{g1,g2}\cdot d_{s1,s2}$
では、実装に移ります。
3.コード
まず、ゲスト5人、5席の場合を考えます。次のようにダミーデータを作成します。
import random
num = 5 # ゲストの人数(席数)
random.seed(1) # 乱数のシード固定
# ゲストのリスト作成
G = ['g{}'.format(g) for g in range(num)]
# 席のリスト作成
S = ['s{}'.format(g) for g in range(num)]
# ゲスト同士の親密度の作成(大きい値ほど親密)
GG2R = {}
for g1 in G:
for g2 in G:
if g2>=g1:continue
r = random.random()
GG2R[g1,g2] = r
GG2R[g2,g1] = r
# 席同士の距離の作成(大きい値ほど近い)
SS2D = {}
for s1 in S:
for s2 in S:
if s2>=s1:continue
d = random.random()
SS2D[s1,s2] = d
SS2D[s2,s1] = d
# 表示
print('G:', G)
print('S:', S)
print('GG2R:')
print(GG2R)
print('SS2D:')
print(SS2D)
標準出力は次のようになります。
G: ['g0', 'g1', 'g2', 'g3', 'g4']
S: ['s0', 's1', 's2', 's3', 's4']
GG2R:
{('g1', 'g0'): 0.13436424411240122, ('g0', 'g1'): 0.13436424411240122, ('g2', 'g0'): 0.8474337369372327, ('g0', 'g2'): 0.8474337369372327, ('g2', 'g1'): 0.763774618976614, ('g1', 'g2'): 0.763774618976614, ('g3', 'g0'): 0.2550690257394217, ('g0', 'g3'): 0.2550690257394217, ('g3', 'g1'): 0.49543508709194095, ('g1', 'g3'): 0.49543508709194095, ('g3', 'g2'): 0.4494910647887381, ('g2', 'g3'): 0.4494910647887381, ('g4', 'g0'): 0.651592972722763, ('g0', 'g4'): 0.651592972722763, ('g4', 'g1'): 0.7887233511355132, ('g1', 'g4'): 0.7887233511355132, ('g4', 'g2'): 0.0938595867742349, ('g2', 'g4'): 0.0938595867742349, ('g4', 'g3'): 0.02834747652200631, ('g3', 'g4'): 0.02834747652200631}
SS2D:
{('s1', 's0'): 0.8357651039198697, ('s0', 's1'): 0.8357651039198697, ('s2', 's0'): 0.43276706790505337, ('s0', 's2'): 0.43276706790505337, ('s2', 's1'): 0.762280082457942, ('s1', 's2'): 0.762280082457942, ('s3', 's0'): 0.0021060533511106927, ('s0', 's3'): 0.0021060533511106927, ('s3', 's1'): 0.4453871940548014, ('s1', 's3'): 0.4453871940548014, ('s3', 's2'): 0.7215400323407826, ('s2', 's3'): 0.7215400323407826, ('s4', 's0'): 0.22876222127045265, ('s0', 's4'): 0.22876222127045265, ('s4', 's1'): 0.9452706955539223, ('s1', 's4'): 0.9452706955539223, ('s4', 's2'): 0.9014274576114836, ('s2', 's4'): 0.9014274576114836, ('s4', 's3'): 0.030589983033553536, ('s3', 's4'): 0.030589983033553536}
次に、数理最適化プログラムのクラスを実装します。
import pulp
import time
class Guests2Seats:
def __init__(self, G, S, GG2R, SS2D, FixGS=[]):
# 入力データ
self.G = G
self.S = S
self.GG2R = GG2R
self.SS2D = SS2D
self.FixGS = FixGS
### モデリング用のリストを作成
# 変数 x 作成用
self.GS = [(g,s) for g in self.G for s in self.S]
# 変数 y 作成用
self.GSGS = [(g1,s1,g2,s2) for (g1,s1) in self.GS for (g2,s2) in self.GS if g1<g2]
# 目的関数定義用(非負の値のみ抽出)
self.GSGS_ = [(g1,s1,g2,s2) for (g1,s1,g2,s2) in self.GSGS if (g1,g2) in self.GG2R and (s1,s2) in self.SS2D]
# 最適化パラメータ
self.timeLimit = 360 # 計算時間[s]
self.msg = 1 # メッセージを(非)表示
self.model_type = 2
# 数理最適化モデルとソルバー
self.x = None
self.model = None
self.solver = None
# 最適化計算結果
self.status = None
self.elapsed_time = None
self.obj = None
self.resGS = None
self.G2G2FD = None
return
def modeling(self, model_type=2):
self.model_type = model_type
### 数理最適化モデルの定義
self.model = pulp.LpProblem('Guests2Seats', pulp.LpMaximize)
### 変数
self.x = pulp.LpVariable.dicts('x', self.GS, cat='Binary')
self.y = pulp.LpVariable.dicts('y', self.GSGS, cat='Binary')
### 制約
# 各ゲストは、1つの席に割り当てる
for g in self.G:
self.model += pulp.lpSum(self.x[g,s] for s in S) == 1
# 各席は、1つのゲストを割り当てられる
for s in self.S:
self.model += pulp.lpSum(self.x[g,s] for g in G) == 1
# ゲストの席への割当xと、2人のゲストの席への割当yの整合性をつける制約
if self.model_type == 2:
for g1,s1,g2,s2 in self.GSGS:
# 1点排除 ✕ 4
self.model += - self.x[g1,s1] - self.x[g2,s2] + self.y[g1,s1,g2,s2] <= 0
self.model += - self.x[g1,s1] + self.x[g2,s2] + self.y[g1,s1,g2,s2] <= 1
self.model += + self.x[g1,s1] - self.x[g2,s2] + self.y[g1,s1,g2,s2] <= 1
self.model += + self.x[g1,s1] + self.x[g2,s2] - self.y[g1,s1,g2,s2] <= 1
elif self.model_type == 3:
for g1,s1,g2,s2 in self.GSGS:
# 1点排除 & 3点排除
self.model += + self.x[g1,s1] + self.x[g2,s2] - self.y[g1,s1,g2,s2] <= 1
self.model += - self.x[g1,s1] - self.x[g2,s2] + 2 * self.y[g1,s1,g2,s2] <= 0
elif self.model_type == 4:
for g1,s1,g2,s2 in self.GSGS:
# 3点排除
self.model += - self.x[g1,s1] - self.x[g2,s2] + 2 * self.y[g1,s1,g2,s2] <= 0
elif self.model_type == 5:
for g1,s1,g2,s2 in self.GSGS:
self.model += self.y[g1,s1,g2,s2] <= self.x[g1,s1]
self.model += self.y[g1,s1,g2,s2] <= self.x[g2,s2]
elif self.model_type == 6:
for g1 in self.G:
for s1 in self.S:
for g2 in self.G:
if not g1<g2:continue
self.model += pulp.lpSum([self.y[g1,s1,g2,s2] for s2 in self.S]) <= self.x[g1,s1]
for g1 in self.G:
for s2 in self.S:
for g2 in self.G:
if not g1<g2:continue
self.model += pulp.lpSum([self.y[g1,s1,g2,s2] for s1 in self.S]) <= self.x[g2,s2]
elif self.model_type == 7:
for g1 in self.G:
for s1 in self.S:
for g2 in self.G:
if not g1<g2:continue
self.model += pulp.lpSum([self.y[g1,s1,g2,s2] for s2 in self.S]) <= self.x[g1,s1]
for g1 in self.G:
for s2 in self.S:
for g2 in self.G:
if not g1<g2:continue
self.model += pulp.lpSum([self.y[g1,s1,g2,s2] for s1 in self.S]) <= self.x[g2,s2]
for s1 in self.S:
for g1 in self.G:
for s2 in self.S:
self.model += pulp.lpSum([self.y[g1,s1,g2,s2] for g2 in self.G if g1<g2]) <= self.x[g1,s1]
for s1 in self.S:
for g2 in self.G:
for s2 in self.S:
self.model += pulp.lpSum([self.y[g1,s1,g2,s2] for g1 in self.G if g1<g2]) <= self.x[g2,s2]
# 予めゲストを特定の席に固定したい場合の制約
for g, s in self.FixGS:
self.model += self.x[g,s] == 1
### 目的関数:ゲスト同士の親密度が高く、席同士の距離が近いほどよい
self.model += pulp.lpSum(self.y[g1,s1,g2,s2] * self.GG2R[g1,g2] * self.SS2D[s1,s2] for g1,s1,g2,s2 in self.GSGS_)
return
def set_option(self, msg, timeLimit, solver='CBC'):
self.msg = msg
self.timeLimit = timeLimit
if solver == 'SCIP':
self.solver = pulp.SCIP(msg=self.msg, timeLimit=self.timeLimit)
else: # CBC
self.solver = pulp.PULP_CBC_CMD(msg=self.msg, timeLimit=self.timeLimit)
return
def solve(self):
start_time = time.time()
# 求解
self.status = self.model.solve(self.solver)
# 時間計測
self.elapsed_time = time.time() - start_time
# 最適化計算結果の整理
# ゲストの席への割当
self.resGS = [(g,s) for g in self.G for s in self.S if self.x[g,s].value()==1]
# 目的関数値の保存
self.obj = self.model.objective.value()
# 各ゲストが親密度の高い人と近くに座ったかの確認用
self.G2G2RD = {}
for g1,s1,g2,s2 in self.GSGS:
self.G2G2RD.setdefault(g1, {})
if self.y[g1,s1,g2,s2].value()==1:
r = GG2R[g1,g2] if (g1,g2) in self.GG2R else 0
d = SS2D[s1,s2] if (s1,s2) in self.SS2D else 0
if r > 0 and d > 0:
self.G2G2RD[g1][g2] = (r, d)
return
def show_result(self, x_flag=False, r_flag=False):
if not self.status==1:return
print('=== Result ===')
print('status:', pulp.LpStatus[self.status])
print('obj:', self.obj)
print('elapsed_time:{:.2f}[s]'.format(self.elapsed_time))
if x_flag:
print('=== x ===')
for g, s in self.resGS:
print(g, '->', s)
return
数理最適化プログラムのクラス設計から理解したい方は、アドベントカレンダー10日目のPythonではじめる数理最適化:クラス設計入門から読み始めるとよいかもしれません。
いくつかポイントをおさせておきます。modelingメソッドでは、引数model_typeで上記の数理最適化モデル②〜⑦に対応できるように2〜7を指定できます。また、コード内にFixGSというリストが作成されており、制約も記述されていることに注意してください。これは、予めゲストを特定の席に固定するための仕掛けで、アドベントカレンダー18日目で20人のゲストの席を決める場合に利用します。目的関数の定義では、リストGSGS_を利用しています。これは目的関数値の計算で親密度が0、または距離が0の項を計算しない工夫になります8。次にset_optionメソッドでは最適化計算に必要なパラメータを設定しています。ここではメッセージの表示/非表示、計算の打ち切り時間に加え、ソルバーの指定も行っています。
クラスが設計されたら、次のコードで最適化計算を実行できます。
# 集合と定数の設定
g2s = Guests2Seats(G, S, GG2R, SS2D)
# 数理モデリング
g2s.modeling(7)
# オプションの設定
g2s.set_option(msg=0, timeLimit=360, solver='CBC')
# 最適化計算
g2s.solve()
# 最適化の結果の表示
g2s.show_result(x_flag=True)
次のような標準出力が得られました。
=== Result ===
status: Optimal
obj: 2.952840010608766
elapsed_time:0.06[s]
=== x ===
g0 -> s0
g1 -> s2
g2 -> s1
g3 -> s3
g4 -> s4
=== Result ===以下の標準出力から最適解が見つかり、目的関数は$2.95$、計算時間は$0.06$秒であることがわかります。
また、=== x ===以下の標準出力から実際の席の割り当ては、ゲスト$g0,g1,g2,g3,g4$はそれぞれ席$s0,s2,s1,s3,s4$に割り当てられることがわかります。とりあえず、数理最適化モデルの実装ができました。一安心です。
3.考察
本記事で作成したダミーデータは数理最適化モデルのテストのために作成しており、席の距離関係がめちゃくちゃであったり、親密度や距離が密なデータであることに注意してください。通常の席決めは、席の近傍以外は距離を0とし、知り合いでなければ親密度も0とするため疎なデータとなります。以下の表は、ソルバーCBCとソルバーSCIPを利用した場合の計算時間の表です。ゲストの人数を5人〜8人として、上記で定めた数理最適化モデル②〜⑥を解いた際の計算時間がわかります9。
ソルバーCBCを利用した場合(2022年12月29日更新)
| ゲストの人数(=席数) | 変数$x$の数 | 変数$y$の数 | ②計算時間(1点排除) | ③計算時間(1点排除&3点排除) | ④計算時間(3点排除&y最大化) | ⑤計算時間(2点排除&y最大化) | ⑥計算時間(2点排除&y最大化&和の利用S) | ⑦計算時間(2点排除&y最大化&和の利用S&G) |
|---|---|---|---|---|---|---|---|---|
| 5 | 25 | 625 | 11.66[s] | 7.56[s] | 4.35[s] | 1.48[s] | 0.65[s] | 0.06[s] |
| 6 | 36 | 1,296 | 45.33[s] | 37.20[s] | 17.76[s] | 8.71[s] | 2.79[s] | 3.39[s] |
| 7 | 49 | 2,401 | 266.57[s] | 144.42[s] | 87.73[s] | 31.12[s] | 13.02[s] | 1.74[s] |
| 8 | 64 | 4,096 | 2451.34[s] | 1049.04[s] | 371.49[s] | 141.36[s] | 7.56[s] | 10.18[s] |
ソルバーSCIPを利用した場合(2022年12月29日更新)
| ゲストの人数(=席数) | 変数$x$の数 | 変数$y$の数 | ②計算時間(1点排除) | ③計算時間(1点排除&3点排除) | ④計算時間(3点排除&y最大化) | ⑤計算時間(2点排除&y最大化) | ⑥計算時間(2点排除&y最大化&和の利用S) | ⑦計算時間(2点排除&y最大化&和の利用S&G) |
|---|---|---|---|---|---|---|---|---|
| 5 | 25 | 625 | 1.49[s] | 1.02[s] | 1.98[s] | 2.72[s] | 0.53[s] | 0.05[s] |
| 6 | 36 | 1,296 | 5.96[s] | 6.08[s] | 5.00[s] | 4.68[s] | 3.83[s] | 2.55[s] |
| 7 | 49 | 2,401 | 26.57[s] | 19.14[s] | 14.12[s] | 15.05[s] | 4.57[s] | 7.46[s] |
| 8 | 64 | 4,096 | 202.21[s] | 115.80[s] | 124.05[s] | 151.31[s] | 16.24[s] | 13.06[s] |
まず、ソルバーCBCを利用した場合について確認します。ゲストの人数に対して非線形に計算時間が増大していることからNP困難な問題に立ち向かっていることを体感できます。また、②を基準にすると③⑤⑥⑦と数理最適化モデルに工夫を重ねることで計算時間が小さくなっていることもわかります。しかし、⑥に対して⑦の工夫(冗長な制約を追加)をした場合には計算時間が悪化する場合もあるようです。数理最適化モデルを構築する際にできるだけ少ない制約で表現することは定石ですが、ソルバーに依存して制約を追加することで高速化される場合があります。実験回数が1回なので安定してませんが、⑥⑦は圧倒的に高速化されていそうなことがわかります。
次にソルバーSCIPを利用した場合について確認します。②を基準に③④⑤⑥⑦は高速化されていますが、なんと④⑤よりも③のほうが高速である場合もあるようです。ただし、⑥⑦が圧倒的に高速であることは間違いなさそうです。整数計画問題では、ソルバーの実装に依存して計算時間が大きく異なる場合があります。それは、前処理や最適化計算中に生成される切除平面などの影響があるためです。
最後に、CBCとSCIPを比較してみます。SCIPがCBCと比べて全体的に高速であることがわかりますが⑥⑦ではCBCのほうが全体的に高速のようです。私の手もとで何度か乱数を変えてデータを生成して実行してみましたが、n=9,10の場合もCBCのほうが高速であるという結果が得られました。
一通り結果を眺めてみましたが、数理最適化モデルとして同値であっても、制約の表現方法が変われば、ソルバーに依存して計算時間が大きく変わることを確認できました。本記事での調査はここで打ち切りますが、高速化の要因をさらに追求するためには、ソルバーの標準出力を確認したり、様々なオプションを設定して実験する必要があります。ここから先の調査は整数計画ソルバーの実装経験がある人のほうがよさそうです10。
4.おわりに
本記事では、非線形な問題を線形な問題に変換する方法を紹介しました。真理値表を用いた1点排除のテクニックを利用することで、目的関数に現れる論理積の非線形性を解消しました。しかし、その副作用として変数の数がゲストの人数に対して指数的に増えることに注意してください。非線形な問題を強引に線形な問題に変換するのですから、それなりの対価を払わなければならないということです。また、本記事で伝えたいこととは異なりますが、様々なみなさまからご提案をいただき、数理最適化モデルの表現方法と探索速度についても深堀りして議論することができました。また、本記事では深入りしませんが一部の0-1整数変数を連続変数にしても整数性を壊さずに最適解を得られることを確認しています。
さて、20人のゲストの席決めなんてできるのでしょうか、不安です。実際、本記事で紹介した方法では、ゲスト20人の最適解をバチッと求めるのは難しいかもしれません。本記事で示したことは「汎用ソルバーで解ける形に表現できる」ことであり、「汎用ソルバーで現実的な時間で解ける」わけではありません。しかし、実際のデータを利用すれば工夫次第でもう少し大きな問題にもアプローチできるので、その方法をアドベントカレンダー18日目の記事で挑戦してみます。工夫とは、初期解を利用する点と乱数を利用する簡単なものです。せっかくなのでアドベントカレンダー9日の記事で得られた席次を初期解に、より目的関数値がよくなる解を探索してみます。ソルバーでバチッと解けない時点であまり格好良くないのですが、泥臭く、カジュアルに数理最適化の技術を使ってみるのが、数理最適化の普及に繋がるのかなと思っています。詳しくは18日のアドベントカレンダーに引き継ぎます。乞うご期待!
本記事が数理最適化の玄人にとって有益な情報になれば幸いです。もし、「Pythonではじめる数理最適化」の続本が出せるなら先日のPythonではじめる数理最適化:クラス設計入門の内容に加えて、本記事の内容も書くかもしれません、、、この機会に書き溜めていこう。
リンク集
- アドベントカレンダー9日目披露宴の席次を Gromov-Wasserstein 最適輸送で決めた話と再現用Colab
- アドベントカレンダー10日目Pythonではじめる数理最適化:クラス設計入門
- 「Pythonではじめる数理最適化」のオーム社のページ
- 「Pythonではじめる数理最適化」のAmazonのページ
-
変数$y_{g1,s1,g2,s2}$について、「岩永が席Aに、太田が席Bにつく」($y_{岩永、席A,大田,席B}=1$)ことと、「太田が席Bにつき、岩永が席Aにつく」($y_{大田,席B,岩永、席A}=1$)ことは同じ意味なので、両方考える必要はなく、片方のみ($g1<g2$)考えれば十分です。なお、変数$y$削減のご指摘はShunjiさんからもいただきました。 ↩
-
変数$x_{g1,s1}$、$x_{g2,s2}$、$y_{g1,s1,g2,s2}$の真理値表から$\{0,1\}$への写像の表す、$\{0,1\}$は$\{False,True\}$の意味になります。 ↩
-
$a\cdot x_{g1,s1} + b \cdot x_{g2,s2} + c \cdot y_{g1,s1,g2,s2} = d$とおいて、$(x_{g1,s1},x_{g2,s2},y_{g1,s1,g2,s2})$=$(0,0,0),(1,1,1)$を通るような平面を求めます。複数点排除をする不等式を見つける方法は私には解けていません。 ↩
-
私は自分で証明をつけたのですが、たぶん誰かが証明をつけていると思うので、もし情報を知ってる人がいたらおしえてください。 ↩
-
今井氏からは真理値表を使わず、論理式「$y_{g1,s1,g2,s2}=1\leftrightarrow (x_{g1,s1}=1 \land x_{g2,s2}=1)$」から論理変換することで、$y_{g1,s1,g2,s2} \leq x_{g1,s1}$と$y_{g1,s1,g2,s2} \leq x_{g2,s2}$の2本の制約が得られることをご提案いただきました。 ↩
-
お風呂に入っているときに思いついたそうです。 ↩
-
ダミーデータは疎ではないため親密度0、距離0のデータがありませんが、アドベントカレンダー18日目で20人のゲストの席を決める場合には親密度0、距離0のデータが多いので、目的関数の簡略化に役立ちます。 ↩
-
計算時間が安定しない整数計画問題の実験に関わらず、実験回数1回であることに注意してください。私の怠惰です。 ↩
-
だれか調査してもらえると嬉しいです。SCIPが遅くなる理由として、余計な前処理が走っているためかもしれなく、もしかしたら特定の処理をOFFにすることで高速化するのでは〜など想像してますが、正直、手を動かしてみないとわかりません。 ↩