Go to Qiita Advent Calendar 2024 Top
LoginSignup
7
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@iwaki2323a

圏論の基本概念をJuliaで実装してみた

Last updated at Posted at 2024-12-17

これは「imtakalab Advent Calendar 2024」の18日目の記事です．

概要

筆者は現在情報学専攻の修士学生です．所属している研究室でJuliaを普及させたいという秘めた野望があるのですが全く流行らず，日々力不足を感じています．

筆者の周囲では，研究でPythonを使っている学生が多いです．Pythonは汎用的で使いやすい言語ですが，場合によっては速度が不十分だったり，数学的概念の記述が直感的でなかったりします．

科学計算に強く，優れた型システムを持ち，強力な多重ディスパッチを備え，動的型付け言語でありながらCに迫る速度を出せるJuliaの有用性を本記事で伝えられればなと思います．

Juliaについて

Juliaはマサチューセッツ工科大学で開発された言語です．
その特徴は「Pythonのように書けて，Cのように動く」ことです1．普段Pythonを使用している方はすぐに習得できると思います．
開発者らは，Juliaを作った理由について「We are greedy: we want more.」と述べています2．開発者たちのブログからは，彼らの熱意とオタク具合がよく伝わってきます．

Pythonユーザはライブラリの数を心配しているかもしれませんが，Juliaも意外と充実しています．機械学習，自然言語処理，ネットワーク科学，GPUの使用，描画ツール，etc...

行列が標準搭載でギリシャ文字が使えたり数式を直感的に書けたりと，科学計算はPythonよりやりやすいと個人的に思います．
また，Pythonとの互換性も充実しており，PythonからJuliaを呼び出したりその逆もできます．Pythonで書いたコードの特定の部分が著しく速度を損なっている場合，その部分のみをJuliaで代替することも可能です．

JuliaのインストールにはJuliaupという公式のバージョン管理ツールを使用することをおすすめします．pyenvのような感じです．

開発環境はVS Codeがおすすめです．うまく動かない場合はVS Codeの設定のJulia: Executable Pathを確認してみてください．

また，開発を進める際はProject環境を作って自作パッケージにするといいでしょう．仮想環境のような感じです．
VS Code画面の左下にあるJulia env:から作成したProject環境を選択するとその環境でコードを実行できます．

VS CodeでJupyterカーネルを使えるようにしておけば，IJuliaパッケージをインストールすることでnotebook環境でJuliaを使用することも可能です．
カーネルにはインストールしたJuliaを選択可能で，先述のようにJulia env:でProject環境を選択するとその環境でコードを動かせます．

圏論について

Juliaを用いた実装例として，圏論という数学理論の一部の基本的概念を取り扱いたいと思います．（本記事は筆者の所属する研究室内向けのもので，研究室の学生にJuliaと共に圏論にも興味を持ってもらいたいという意図があります．）

圏論 (category theory) は，Samuel EilenbergとSaunders MacLaneによって1945年に発表されました3．圏論とは，数学的構造とその間の関係を抽象的に扱う数学理論の一つです4．数学者のSteve Awodeyは著書で「圏論とは何か？」という問いに次のように答えています5．

"As a first approximation, one could say that category theory is the mathematical study of (abstract) algebras of functions."
「おおまかに言えば，圏論とは関数の（抽象）代数を数学的に研究する分野である．」

圏論は計算機科学にも大きな影響を及ぼしています．Haskellではモナドという圏論の概念を利用して透過性を損なうことなく副作用のある操作を実現しています．筆者はまだまだ勉強中のためこの辺はよくわかっていません．
近年，Haskellの潮流に乗った型付き関数型プログラミング言語が台頭していることから，型システムの理解や設計に関するスキルを高める上で，圏論を学ぶことは有益だと考えます．

本記事では圏論の概念のうち，圏 (category)，対象 (object)，射 (arrow)，関手 (functor)，自然変換 (natural transformation) を扱います．記事がとんでもなく長くなってしまうため説明はざっくりです．

筆者は決して数学に強いわけではなく圏論も勉強中のため，お手柔らかに最後までお付き合いいただけると幸いです．

実装と解説

こちらが本記事を書くにあたって作成したコードです．

Juliaの開発環境を整備した後，Readmeに沿って実行してもらえば動かせると思います．

圏，対象，射

圏とは，対象と射からなるシステムです6．
対象同士の関係を射で記述します．

$\mathbf{Definition~1.}$ 圏は以下の要素から構成される．

  • 対象 (Objects): $A, B, C, ...$
  • 射 (Arrows): $f, g, h, ...$
  • 各射は域 (domain)と余域 (codomain) と呼ばれる対象を持つ．
    $$dom(f), ~~cod(f)$$
    • $f: A \rightarrow B$ は，$A = dom(f)$ かつ $B = cod(f)$ であることを示す．
  • $cod(f) = dom(g)$ である射$f: A \rightarrow B$ と射 $g: B \rightarrow C$ が与えられたとき，$f$と$g$の合成射が存在する．
    $$g \circ f: A \rightarrow C$$
  • 各対象には恒等射が存在する．対象$A$の恒等射は以下のように書く．
    $$1_A: A \rightarrow A$$
  • 上記の要素は以下の法則に従う．
    • 結合律 (Associativity): 射$f: A \rightarrow B$，$g: B \rightarrow C$，$h: C \rightarrow D$について
      $$h \circ (g \circ f) = (h \circ g) \circ f$$
    • 単位律 (Unit): 射$f: A \rightarrow B$について
      $$f \circ 1_A = f = 1_B \circ f$$

圏の中身は上の定義を満たしていれば何でもいいです．
今回は半順序集合 (poset) を例に話を進めたいと思います．

射の実装

domとcodをpropertyに持つ構造体として射を定義します．
対象は何でも良いということでパラメトリック型にしています．

arrow.jl
mutable struct Arrow{T}
    dom::T # 域 (domain)
    cod::T # 余域 (codomain)
    # 内部コンストラクタ
    Arrow(dom::Any, cod::Any) = new{Any}(dom, cod)
    Arrow(dom::Int, cod::Int) = new{Int}(dom, cod)
    Arrow(dom::String, cod::String) = new{String}(dom, cod)
    Arrow(dom::Float64, cod::Float64) = new{Float64}(dom, cod)
    Arrow(dom::Symbol, cod::Symbol) = new{Symbol}(dom, cod)
end

圏の実装

対象の集合objectsと射の集合arrowsをpropertyに持つ構造体として圏を定義します．
内部コンストラクタは複数作成したのですが，ここでは一部のみ載せています．

category.jl
# 痩せた圏
mutable struct ThinCategory <: AbstractCategory
    objects::Set{Any}
    arrows::Set{<:Arrow}
    # 内部コンストラクタ
    # 対象と射を入力として生成
    function ThinCategory(objects::Set, arrows::Set{<:Arrow})
        arrows = copy(arrows)
        # 恒等射の追加
        for object in objects
            push!(arrows, Arrow(object, object))
        end
        new(objects, arrows)
    end

今回は痩せた圏と呼ばれる，domとcodが同じ射は高々一つしか存在しない圏を想定します．
したがって，射を集合で扱う上で等価性を定義する必要が出てきます．
Juliaには多重ディスパッチという，同じ関数名でも引数の型によって別々の関数を呼び出すことができるという機能があります．つまり，標準搭載の==という演算子にArrow型が引数のときの演算を追加できるということです．

arrow.jl
# 等価性の定義
# domとcodが同じなら等価
function Base.:(==)(arrow1::Arrow, arrow2::Arrow)::Bool
    arrow1_props = tuple([getproperty(arrow1, prop) for prop in propertynames(arrow1)]...)
    arrow2_props = tuple([getproperty(arrow2, prop) for prop in propertynames(arrow2)]...)
    return arrow1_props == arrow2_props
end
# ハッシュの定義
function Base.hash(arrow::Arrow, h::UInt)::UInt
    arrow_props = tuple([getproperty(arrow, prop) for prop in propertynames(arrow)]...)
    return hash(arrow_props, h)
end

こうすることで，Arrow(1, 2) == Arrow(1, 2)がtrueとなるのはもちろん，inなどの演算子もしっかり機能します．
SetやDictといったハッシュベースのコレクションに対応するため，hash関数も追加しています． これにより，重複を含んだArrowの配列をSetにしても，ちゃんと重複が無くなります．

多重ディスパッチのおかげで自身で定義した構造体をより自然な形で扱うことが可能になります．構造体に対して四則演算を自由に定義できるということなので，柔軟に代数的構造を表現することができます．
また，引数によって処理を変えたい関数がある場合，中でif分岐するのではなく多重ディスパッチにすることで効率がよくなる場合があります．

射の合成

入力の圏において可能な合成射を全て作成する関数です．
今回has_arrow関数によるチェックは不要ですが，今後を考え一応入れました．

category.jl
function compose(C::ThinCategory)::ThinCategory
    C = copy(C)
    for arrow1 in C.arrows
        for arrow2 in Set(arrow for arrow in C.arrows if arrow.dom == arrow1.cod)
            # すでに射がある場合は除外
            if !has_arrow(C, arrow1.dom, arrow2.cod)
                # 射の追加
                push!(C.arrows, Arrow(arrow1.dom, arrow2.cod))
            end
        end
    end
    return C
end

関手

関手とは2つの圏の間の対応づけです．
ある圏のこの対象は別の圏だとこの対象，この射は別の圏だとこの射，みたいな対応を関手で考えます．
その時，元の圏の構造を反映したような対応づけが求められます．
徐倫がアイリンに対応づき，アナスイがアナキスに対応づくみたいな感じです7．

$\mathbf{Definition~2.}$ 関手
$$F: \mathbf C \rightarrow \mathbf D$$
は圏$\mathbf C$から圏$\mathbf D$の，対象は対象へ，射は射への以下の条件を満たしたマッピングである．

  • 域と余域の保存: $F(f: A \rightarrow B) = F(f): F(A) \rightarrow F(B)$
  • 恒等射の保存: $F(1_A)$ = $1_{F(A)}$
  • 合成の保存: $F(g \circ f) = F(g) \circ F(f)$

関手$F$が圏$\mathbf C$の射$f: A \rightarrow B$を圏$\mathbf D$の射$g: C \rightarrow D$に移すときは以下のように書けます．
$$
F(f) = g, ~~F(A) = C, ~~F(B) = D
$$
先の例で考えると，$MadeInHaeven(徐倫) = アイリン$と書けるわけです．エンポリオはエンポリオです．

関手の実装

前述の通り，関手はマッピングであるためDictで十分です．
作成した2つの圏間の射のマッピングが関手の条件を満たすかを判定する関数を作成しました．

functor.jl
# 射の対応づけが関手をなしているかの検証
function is_functorial(C::ThinCategory, D::ThinCategory, mapping::Dict{Arrow, Arrow})::Bool
    # mappingにobjectも追加
    mapping = add_objects_to_map(mapping)
    # mappingから関手Fを作成 (写像の形で)
    F(x) = mapping[x]

    # 合成射を保存するか
    for arrow1 in C.arrows
        for arrow2 in Set(arrow for arrow in C.arrows if arrow.dom == arrow1.cod)
            # 圏Cの2つの射を関手Fで移した先でも合成可能かつその合成射が圏Dにあるか
            if !(F(arrow1).cod == F(arrow2).dom && has_arrow(D, F(arrow1).cod, F(arrow2).dom))
                return false
            end
        end
    end
    # 恒等射を保存するか
    for arrow in get_identity_arrows(C)
        obj = arrow.dom
        F_id = F(arrow)
        id_F = Arrow(F(obj), F(obj))
        if F_id != id_F
            return false
        end
    end
    return true
end

Juliaは関数の定義をf(x) = 2xというように簡単に行えます．これを利用して関手$F$を関数として1行で定義できました．
さらに，Juliaの描画機能ではこうした関数をそのまま描画関数に入力できます．例えば冪乗則 (power law) をグラフに追加したいとき，非常に直感的なコードで描画できるというわけです．好き．

自然変換

自然変換とは2つの関手の対応づけです．
ある圏から別のある圏への関手は複数考えられます．圏同士のマッピングである関手同士のマッピングを考えるということです．

$\mathbf{Definition~3.}$ 2つの圏$\mathbf C, \mathbf D$と$\mathbf C$から$\mathbf D$への2つの関手$F, G: \mathbf C \rightarrow \mathbf D$について，自然変換$\vartheta: F \rightarrow G$とは圏$\mathbf D$の射の族である．
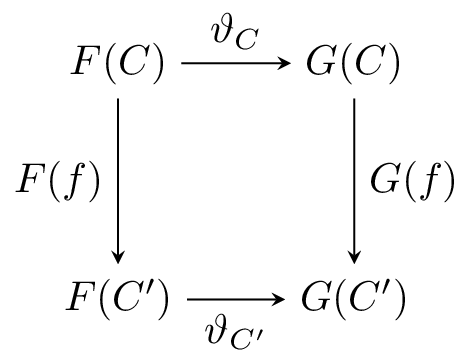
どんな圏$\mathbf C$の射$f: C \rightarrow C'$についても，$\vartheta_{C'} \circ F(f) = G(f) \circ \vartheta_C$となる．これは以下の図式が可換性を満たすということである．

commutes_figure

可換性を満たすということは，この図において$F(f)$を通ってから$\vartheta_C'$を通る経路と$\vartheta_C$を通ってから$G(f)$を通る経路で行き着く先が同じだということです．

自然変換の実装

任意の関手から関手へのマッピングが自然変換であるかを判別する関数を以下のように実装しました．

natural_transformation.jl
function is_natural(C::ThinCategory, F_mapping::Dict{Any, Any}, G_mapping::Dict{Any, Any})::Bool
    F = x -> F_mapping[x]
    G = x -> G_mapping[x]

    # 自然変換
    ϑ_mapping = Dict{Any, Arrow}(
        (obj, Arrow(F(obj), G(obj))) for obj in C.objects
    )
    ϑ = x -> ϑ_mapping[x]
    for arrow in C.arrows
        # 合成可能か & 可換性を満たしているか
        if !(ϑ(arrow.dom).cod ==  G(arrow).dom && # 合成できるか ↓→
            F(arrow).cod == ϑ(arrow.cod).dom && # 合成できるか →↓
            G(arrow).cod == ϑ(arrow.cod).cod) # 行き先が同じか
            return false
        end
    end
    return true
end

Juliaではギリシャ文字や数学記号をそのまま使えます．not inという演算を∉で行えたり，上のコードのように$\vartheta$もϑとしてそのまま使えます．
さらに，エディタやREPLで\notinや\varthetaと打つと該当する記号に変換してくれます．この辺の記号はLatexの感覚のまま打ち込めるというわけです．

動かしてみる

posetの圏を例に取り，実際にモジュールを動かしてみたいと思います．

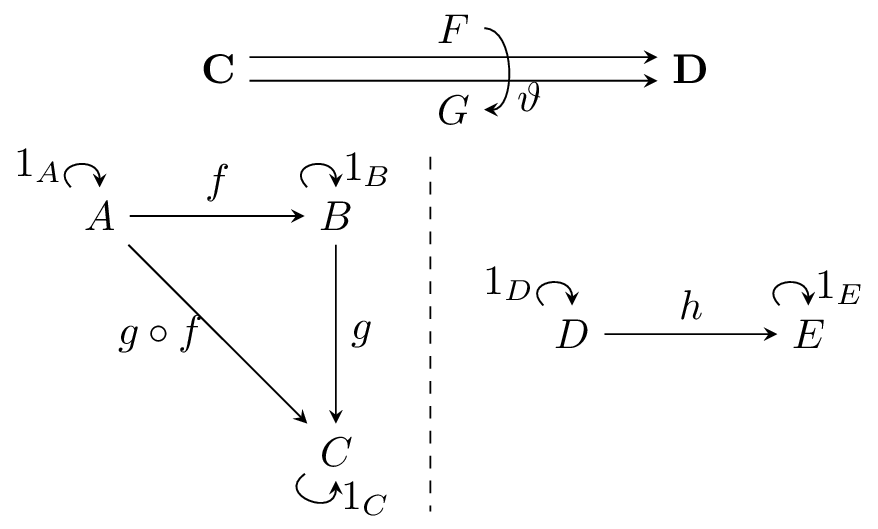
圏$\mathbf C, \mathbf D$をそれぞれ以下のように設定し，その間の関手$F, G$，さらにその間の自然変換$\vartheta$を考えます．

poset.png

圏の射は対象間の順序関係を表現しています．つまり，$f: A \rightarrow B$は$A \leqq B$ということです．
関手は圏$\mathbf C$の順序関係の構造を保存した形で，全ての要素を圏$\mathbf D$の要素へと移すマッピングです．

下は，作成したモジュールでこの2つの圏間の可能な関手を全て列挙し，その間の自然変換の有無を出力するコードです．

sample.jl
using CategoryModule

function main()
    # 圏の定義と射の合成
    C = compose(ThinCategory(["A" "B"; "B" "C"]))
    D = compose(ThinCategory(["D" "E";]))
    # 関手の列挙
    functors = find_functors(C, D)
    # 関手の辞書
    functor_dict = Dict{String, Dict{Any, Any}}()
    # 関手の表示
    println("Functors")
    for (i, functor) in enumerate(functors)
        id = "F" * string(i)
        println(repeat(" ", 3), id, ":")
        functor_dict[id] = functor
        for (dom, cod) in pairs(functor)
            println(repeat(" ", 6), dom, " => ", cod)
        end
    end
    # 自然変換の有無
    println()
    println("Natural tranformations")
    for (id1, f1) in pairs(functor_dict)
        for (id2, f2) in pairs(functor_dict)
            if id1 != id2
                if is_natural(C, f1, f2)
                    println(repeat(" ", 3), id1, " => ", id2)
                end
            end
        end
    end
end

利便性のため，Matrix型を用いた辺リストの形で射を記述し，それを元に圏を生成できるようにしてあります．

また，詳細は割愛しますが可能な関手を列挙するfind_functors関数も実装してあります．この関数は圏$\mathbf C$の射から圏$\mathbf D$の射への可能な写像を全て列挙し，その中からis_functorial関数で関手の条件を満たしているものをピックアップします．

しかし，写像の列挙の計算量は$|\mathbf Dの射の数|^{|\mathbf Cの射の数|}$となるため，対象を少しでも増やすと計算量が爆発するという全く実用性のない機能となっています．

出力結果 
Functors
   F1:
      Arrow("C", "C") => Arrow("D", "D")
      Arrow("B", "C") => Arrow("D", "D")
      Arrow("A", "C") => Arrow("D", "D")
      Arrow("B", "B") => Arrow("D", "D")
      B => D
      A => D
      C => D
      Arrow("A", "B") => Arrow("D", "D")
      Arrow("A", "A") => Arrow("D", "D")
   F2:
      Arrow("C", "C") => Arrow("E", "E")
      Arrow("B", "C") => Arrow("E", "E")
      Arrow("A", "C") => Arrow("D", "E")
      Arrow("B", "B") => Arrow("E", "E")
      B => E
      A => D
      C => E
      Arrow("A", "B") => Arrow("D", "E")
      Arrow("A", "A") => Arrow("D", "D")
   F3:
      Arrow("C", "C") => Arrow("E", "E")
      Arrow("B", "C") => Arrow("E", "E")
      Arrow("A", "C") => Arrow("E", "E")
      Arrow("B", "B") => Arrow("E", "E")
      B => E
      A => E
      C => E
      Arrow("A", "B") => Arrow("E", "E")
      Arrow("A", "A") => Arrow("E", "E")
   F4:
      Arrow("C", "C") => Arrow("E", "E")
      Arrow("B", "C") => Arrow("D", "E")
      Arrow("A", "C") => Arrow("D", "E")
      Arrow("B", "B") => Arrow("D", "D")
      B => D
      A => D
      C => E
      Arrow("A", "B") => Arrow("D", "D")
      Arrow("A", "A") => Arrow("D", "D")

Natural tranformations
   F3 => F1
   F3 => F2
   F3 => F4
   F1 => F3
   F1 => F2
   F1 => F4
   F2 => F3
   F2 => F1
   F2 => F4
   F4 => F3
   F4 => F1
   F4 => F2

結果を見ると，4つの関手が見つかっています．
以下のような内容の関手です．

  • 圏$\mathbf C$の全ての対象を$D$に移す関手
  • 同様に全ての対象を$E$に移す関手
  • $A, B$を$D$に移し$C$を$E$に移す関手
  • $A$を$D$に移し，$B, C$を$E$に移す関手

どの関手もちゃんと順序関係を保存できていますね．
また，自然変換は全ての関手の順序対に対して存在しているということになりました．
正しい結果が出たと思われます．

おわりに

今回はJuliaを使って圏論の基本概念の簡単な実装をしてみました．
圏論という小難しい題材を採用してしまったがために，Juliaのことも圏論のことも十分に伝わらないという有り様になってしまったことに対しては弁解の余地もありません．反省はしていません．

最後に，Juliaのパフォーマンスを上げるためのtipsをまとめている公式ドキュメントを紹介しておきます．

筆者は非常に参考になりました．
このドキュメント内には以下のような記述があります8．

"Once one learns to appreciate multiple dispatch, there's an understandable tendency to go crazy and try to use it for everything."
「一度多重ディスパッチのありがたみを知ると，狂ったように何にでもそれを使おうとするようになることは理解できる．」

Julia覚えたてでウキウキだった筆者には突き刺さり，ひどく取り乱し，素数を数えて落ち着いたことは言うまでもりません．
Juliaを学び始めた後輩にこの言葉を浴びせてやることが，研究室でJuliaの布教活動をしている私の最大の目的であることはここだけの話です．

  1. 進藤 裕之, 佐藤 建太 (2020).「1から始めるJuliaプログラミング」 コロナ社. ISBN 978-4-339-02905-5. ↩

  2. Jeff Bezanson, Stefan Karpinski, Viral B. Shah, Alan Edelman (2012). "Why We Created Julia" https://julialang.org/blog/2012/02/why-we-created-julia/ ↩

  3. Eilenberg, Samuel; MacLane, Saunders (1945). “General Theory of Natural Equivalences”. Transactions of the American Mathematical Society 58 (2): 231–294. doi:10.2307/1990284. ISSN 0002-9947. ↩

  4. 圏論 - Wikipedia ↩

  5. Steve Awodey (2010). "Category Theory -Second Edition-" Oxford University Press. ISBN 9780199237180. ↩

  6. 西郷 甲矢人，能美 十三 (2019).「圏論の道案内 〜矢印でえがく数学の世界〜」 技術評論社. ISBN 978-4-297-10723-9. ↩

  7. 荒木 飛呂彦 (2003). 「ストーンオーシャン 17巻」 集英社. ISBN 4-08-873483-1. ↩

  8. "Performance Tips・The Julia Language -The dangers of abusing multiple dispatch (aka, more on types with values-as-parameters)-" ↩

7
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
7
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?