Pyroで混合ガウスモデルの推定を試してみました。
公式のexampleをベースにして、適宜補足的な内容を入れながら実行しています。
※本記事のソースコードは、Jupyter Notebookで実行しています。
環境
Windows10 Python: 3.7.7 Jupyter Notebook: 1.0.0 PyTorch: 1.5.1 Pyro: 1.4.0 scipy: 1.5.2 numpy: 1.19.1 matplotlib: 3.3.0 seaborn: 0.10.1※Pyroについて他の記事も書いているので、よろしければご覧ください
【Python】Pyroでベイズ推定
import os
import numpy as np
from scipy import stats
import torch
import pyro
import pyro.distributions as dist
from pyro import poutine
from pyro.infer.autoguide import AutoDelta
from pyro.optim import Adam
from pyro.infer import SVI, TraceEnum_ELBO, config_enumerate, infer_discrete
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
pyro.set_rng_seed(0)
pyro.enable_validation(True)
データの準備
seabornからirisデータセットを呼び出し、petal_lengthの値を対象のデータとします。
df = sns.load_dataset('iris')
data = torch.tensor(df['petal_length'], dtype=torch.float32)
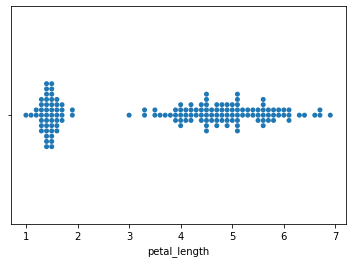
sns.swarmplot(data=df, x='petal_length')
プロットを見ると、クラスタを2個に分けるのが良さそうです 1
modelの設定
Pyroでは、modelメソッドに分布のモデルを記述します。
データ$x_1, \cdots, x_n \in \mathbb{R}$の各クラスタを$z_1, \cdots, z_n \in \{ 1, \cdots, K \}$として、混合ガウスモデルを適用します。
\begin{align}
p &\sim Dir(\tau_0/K, \cdots, \tau_0/K) \\
z_i &\sim Cat(p) \\
\mu_k &\sim N(\mu_0, \sigma_0^2) \\
\sigma_k &\sim InvGamma(\alpha_0, \beta_0) \\
x_i &\sim N(\mu_{z_i}, \sigma_{z_i}^2)
\end{align}
$K$はクラスタの数、$\tau_0, \mu_0, \sigma_0, \alpha_0, \beta_0$は事前分布のパラメータです。2
$\mu_1, \cdots, \mu_K$及び$\sigma_1, \cdots, \sigma_K$をベイズ推定し、クラスタ$z_1, \cdots, z_n$を確率的に算出するモデルを作成します。
K = 2 # Fixed number of clusters
TAU_0 = 1.0
MU_0 = 0.0
SIGMA_0_SQUARE = 10.0
ALPHA_0 = 1.0
BETA_0 = 1.0
@config_enumerate
def model(data):
alpha = torch.full((K,), fill_value=TAU_0)
p = pyro.sample('p', dist.Dirichlet(alpha))
with pyro.plate('cluster_param_plate', K):
mu = pyro.sample('mu', dist.Normal(MU_0, SIGMA_0_SQUARE))
sigma = pyro.sample('sigma', dist.InverseGamma(ALPHA_0, BETA_0))
with pyro.plate('data_plate', len(data)):
z = pyro.sample('z', dist.Categorical(p))
pyro.sample('x', dist.Normal(locs[z], scales[z]), obs=data)
@config_enumerateは、離散変数pyro.sample('z', dist.Categorical(p))を並列的にサンプリングするためのデコレータです。
サンプリングされた値の確認
poutine.traceを使うことで、modelにデータを与えた場合のサンプリング値を確認することができます。
trace_model = poutine.trace(model).get_trace(data)
tuple(trace_model.nodes.keys())
> ('_INPUT',
'p',
'cluster_param_plate',
'mu',
'sigma',
'data_plate',
'z',
'x',
'_RETURN')
trace_model.nodesの型はOrderedDictで、上記のkeyを保持しています。
_INPUTはmodelに与えられたデータ、_RETURNはmodelの返り値(この場合はNone)、それ以外はmodel内で定義したパラメータを指します。
試しに、pの値を確認してみましょう。これは、$Dir(\tau_0/K,⋯,\tau_0/K)$からサンプリングされるパラメータです。
trace_model.nodes['p']もdictであり、valueで値を見ることができます。
trace_model.nodes['p']['value']
> tensor([0.8638, 0.1362])
次に、各データのクラスタを表すzの値を確認してみましょう。
trace_model.nodes['z']['value']
> tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0,
0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1,
0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0,
0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 1, 0])
pの値から0がサンプリングされやすいと言えますが、その通りの結果になっています。
これは事前分布からのサンプリングなので、まだ正しい推定をできないことに注意してください。
guideの設定
Pyroではguideに事後分布を設定します。pyro.infer.autoguide.AutoDeltaは、MAP推定を行うためのクラスです。
guide = AutoDelta(poutine.block(model, expose=['p', 'mu', 'sigma']))
poutine.blockは、推定の対象とするパラメータを選ぶメソッドです。
AutoDeltaでは離散的なパラメータzを扱えないようなので、exposeで指定していません。zの推定は、分布のフィッティングの後に行います。
このguideは、データに対して、推定した値のパラメータをdictで返します。
guide(data)
> {'p': tensor([0.5000, 0.5000], grad_fn=<ExpandBackward>),
'mu': tensor([4.0607, 2.8959], grad_fn=<ExpandBackward>),
'sigma': tensor([1.3613, 1.6182], grad_fn=<ExpandBackward>)}
現時点では初期値を返しているだけですが、これから、SVIによるフィッティングでMAP推定された値を返すようにします。
分布のフィッティング
guideでは、zを推定せずに他のパラメータを推定するモデルを構成しました。
つまり、zを周辺化して計算する必要があります。
これを行うため、確率的変分推定のlossにTraceEnum_ELBO()を設定します。
optim = pyro.optim.Adam({'lr': 1e-3})
svi = SVI(model, guide, optim, loss=TraceEnum_ELBO())
フィッティングを行います。
NUM_STEPS = 3000
pyro.clear_param_store()
history = []
for step in range(1, NUM_STEPS + 1):
loss = svi.step(data)
history.append(loss)
if step % 100 == 0:
print(f'STEP: {step} LOSS: {loss}')
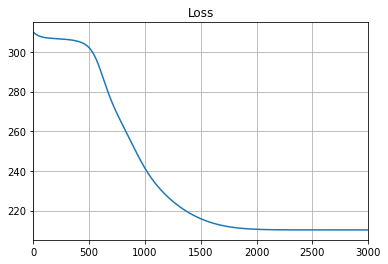
各ステップにおけるlossをプロットすると、次のようになります。
plt.figure()
plt.plot(history)
plt.title('Loss')
plt.grid()
plt.xlim(0, 3000)
plt.show()
lossの値が収束しており、推定が終わっていると判断できます。
推定した分布の確認
$p,\mu, \sigma$の推定値をguideから取得します。
map_params = guide(data)
p = map_params['p']
mu = map_params['mu']
sigma = map_params['sigma']
print(p)
print(mu)
print(sigma)
> tensor([0.6668, 0.3332], grad_fn=<ExpandBackward>)
tensor([4.9049, 1.4618], grad_fn=<ExpandBackward>)
tensor([0.8197, 0.1783], grad_fn=<ExpandBackward>)
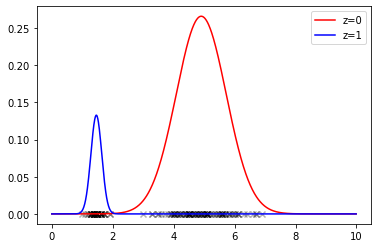
分布をプロットします。
下図で、xマークのプロットはデータの値を意味しています。
x = np.arange(0, 10, 0.01)
y1 = p[0].item() * stats.norm.pdf((x - mu[0].item()) / sigma[0].item())
y2 = p[1].item() * stats.norm.pdf((x - mu[1].item()) / sigma[1].item())
plt.figure()
plt.plot(x, y1, color='red', label='z=0')
plt.plot(x, y2, color='blue', label='z=1')
plt.scatter(data.numpy(), np.zeros(len(data)), color='black', alpha=0.3, marker='x')
plt.legend()
plt.show()
分布をうまく推定できています。
クラスタの推定
まず、guideにて推定されたパラメータをmodelに設定します。
Pyroでは、traceを経由してパラメータを設定します。
trace_guide_map = poutine.trace(guide).get_trace(data)
model_map = poutine.replay(model, trace=trace_guide_map)
modelに設定されたパラメータを確認します。ここでは$\mu$だけ確認します。
trace_model_map = poutine.trace(model_map).get_trace(data)
trace_guide_map.nodes['mu']['value']
>> tensor([4.9048, 1.4618], grad_fn=<ExpandBackward>)
guideの$\mu$の値と一致していますね。
次に、各データの$z$の値を推定します。このとき、pyro.infer.infer_discreteを使います。
model_map = infer_discrete(model_map, first_available_dim=-2)
first_available_dim=-2は、data_plateの次元との衝突を避けるための設定です。
これによって$z$の推定値がmodelに設定されたので、traceから取得することができます。
trace_model_map = poutine.trace(model_map).get_trace(data)
z_inferred = trace_model_map.nodes['z']['value']
z_inferred
> tensor([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0])
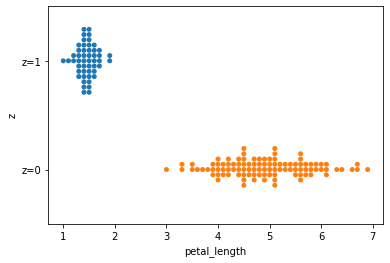
$z$の値ごとにデータをプロットしてみます。
df['z'] = trace_model_map.nodes['z']['value']
df['z'] = df['z'].apply(lambda z: f'z={z}')
sns.swarmplot(data=df, x='petal_length', y='z')
うまく推定できることが分かります。
おわりに
Pyroで混合ガウスを構成し、フィッティングさせてみました。
私はオブジェクト指向的な考え方に慣れているため、推定した値を取り出すのにpoutine.traceを使うのは少し面倒だと感じました。
実際に使うときには、GaussianMixtureModelのようなクラスを作って、値を取り出す処理を内部に記述した方が良さそうです。
Pyroについては、今後も触ってみて理解を深めようかと思います。