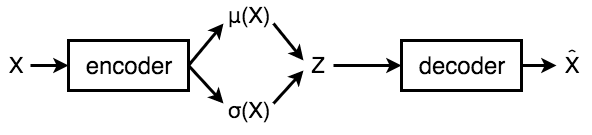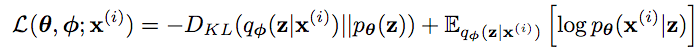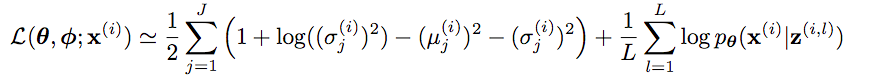はじめに
Variational Autoencoder(VAE)とは、オートエンコーダーを用いた生成モデルの1つです。
論文はこちら:https://arxiv.org/pdf/1312.6114.pdf
kerasでの実装例があまりなかったのと、忘れないようにということでまとめておきます。実装メインのため、原理、数式などはその他の解説記事に任せます。
今回は、kerasの公式ブログ[*1] を参考にしつつ実装を行なっていきます。公式ブログでは、そのほかのオートエンコーダーの実装も書いてあるので非常におすすめです。また、VAEの解説はこちら[*2]がわかりやすかったので、参考にさせていただきました。
VAEとは
まず、通常のオートエンコーダーでは、出力データが入力データとが同じになるように学習を行なって行きます。この時、中間層の素子数を入力層と出力層の素子数より少なくすることで、主成分分析のように入力データの特徴量(潜在変数)を獲得することができます。
VAEでは、通常のオートエンコーダーとは異なり、潜在変数が正規分布となることを仮定します。エンコーダーでは、正規分布のパラメタである、平均と分散を出力させます。
ネットワークの構造がわかれば、実装していけるかと思います。損失関数は後ほど。
モデルの構築
まずは、エンコーダーです。平均と分散を出力する簡単なモデルです。
def build_encoder(self):
x = Input(shape=(original_dim, ))
hidden = Dense(intermediate_dim, activation='relu')(x)
z_mean = Dense(latent_dim, activation='linear')(hidden)
z_sigma = Dense(latent_dim, activation='linear')(hidden)
return Model(x, [z_mean, z_sigma])
入力次元、出力次元はあらかじめ設定しておきます。
次にデコーダーです。
def build_decoder(self):
z_mean = Input(shape=(latent_dim ))
z_sigma = Input(shape=(latent_dim, ))
z = Lambda(self.sampling, output_shape=(latent_dim))([z_mean, z_sigma])
h_decoded = Dense(intermediate_dim, activation='relu')(z)
x_decoded_mean = Dense(original_dim, activation='sigmoid')(h_decoded)
return Model([z_mean, z_sigma], x_decoded_mean)
エンコーダーの出力した平均と分散を入力として受け取り、入力データと同じ次元のものが出力されるようにモデルを組んで行きます。
ここで、3行目にKerasのカスタムレイヤー[*3]を用いています。
理由は、平均と分散から潜在変数zを求めるのですが、直接、潜在変数の確率分布を求めるのでは、逆誤差伝播方が使えなくなるという問題が発生するため、zを次のように置き換える必要があるからです。
次のように書き換えます。
$z=\mu(X) + \epsilon * \sigma (X)$
ただし、$\epsilon〜N(0,I)$
これは、Reparameterization Trickという手法だそうです。
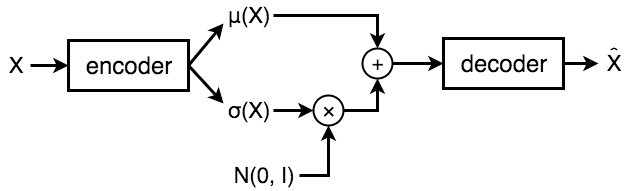
モデルは次のようになります。
このようなレイヤーを実装するため、layer.core.Lambdaを用いてカスタムレイヤーを作成しています。
def sampling(self, args):
z_mean, z_sigma = args
epsilon = K.random_normal(shape=(self.z_dim,), mean=0., stddev=epsilon_std)
return z_mean + z_sigma * epsilon
エンコーダーとデコーダーのモデルができたのであとは、これらをつなぎ合わせて行きましょう。
def build_vae(self, encoder, decoder):
_, encoder_dense, encoder_mean, encoder_sigma = encoder.layers
x = Input(shape=(self.input_dim, ))
hidden = encoder_dense(x)
z_mean = encoder_mean(hidden)
z_sigma = encoder_sigma(hidden)
self.z_m = z_mean # 損失関数で使う
self.z_s = z_sigma # 損失関数で使う
_, _, decoder_lambda, decoder_dense1, decoder_dense2 = decoder.layers
z = decoder_lambda([z_mean, z_sigma])
h_decoded = decoder_dense1(z)
x_decoded_mean = decoder_dense2(h_decoded)
return Model(x, x_decoded_mean)
オートエンコーダーを使うときは、エンコーダーにのみ、または、デコーダーにのみ、入力したかったり出力が欲しい場合があるので、それぞれ別のモデルとして定義しています。
損失関数
VAEでは、損失関数は次のようになります。
1項目は、デコーダーの出力分布$p_\theta(z)$とエンコーダーの出力分布$q_\phi(z|X)$のカルバックライブラー距離です。2項目は、エンコーダーで予測した$z$を用いた$q_\phi(z|X)$に関する、対数尤度$log\ p_\theta(X|z)$の期待値を表します。1項目は小さく、2項目は大きくなるように学習します。
さらに、損失関数の1項目と2項目を近似式で置き換えると次のようになります。
この損失関数はKerasにはないので、自ら作成する必要があります。kerasの損失関数を作る場合[*4]は、各データ点に対してスカラを返し、正解値(y_true)、予測値(y_pred)をとる関数をオブジェクトとして渡してあげれば良いみたいです。
def binary_crossentropy(self, y_true, y_pred):
return K.sum(K.binary_crossentropy(y_pred, y_true), axis=-1)
def vae_loss(self, x, x_decoded_mean):
z_mean = self.z_m
z_sigma = self.z_s
# 1項目の計算
latent_loss = - 0.5 * K.mean(K.sum(1 + K.log(K.square(z_sigma)) - K.square(z_mean) - K.square(z_sigma), axis=-1))
# 2項目の計算
reconst_loss = K.mean(self.binary_crossentropy(x, x_decoded_mean),axis=-1)
return latent_loss + reconst_loss
def model_compile(self, model):
model.compile(optimizer='rmsprop', loss=self.vae_loss)
kerasの公式では、2項目の計算は、
xent_loss = objectives.binary_crossentropy(x, x_decoded_mean)
となっていますが、このままではうまくいかない[*5]ので、修正を行なっています。
1項目、2項目ともにK.meanを入れてますが、こちらも参考サイト[*5]と同じ仕様にしてます。
まとめ
Kerasを使ってVAEを実装してみました。モデルができたので、あとは好きなデータを渡していろいろ遊んでみることができるかと思います。モデルの大まかな構造がわかれば、その後数式を追うのもわかりやすくなるかと思います。レイヤーや損失関数の作成は、初めてやったので今後の参考になりそうです。
引用
- The Keras Blog :https://blog.keras.io/building-autoencoders-in-keras.html
- Variational Autoencoder徹底解説: https://qiita.com/kenmatsu4/items/b029d697e9995d93aa24
- Kerasレイヤーを作成:https://keras.io/ja/layers/writing-your-own-keras-layers/
- 損失関数:https://keras.io/ja/losses/
- KerasでVariational AutoEncoder:http://sh-tatsuno.com/blog/index.php/2016/07/30/variationalautoencoder/