最小二乗法のアルゴリズムを理解したのでメモ。そしてPythonで書いてみた。

概要

最小二乗法について説明します。
はじめ具体的な数値で計算し、次に一般式を求め、最後にPythonで実装します。

最小二乗法って？

サンプルデータがもっともよく当てはまるような式を導き出だして、新しいデータの数値を予測する方法を回帰分析といい、その代表的な手法の一つです。サンプルデータと式から得られる値の誤差が、最小になるような関係式を導き出します。

具体例

はつか大根の成長を予測するとします。
現在、４日目で、葉っぱが何センチ出ているかを、毎日測定しています。

１日目	２日目	３日目	４日目
$0.3$	$1.9$	$2.8$	$4.3$

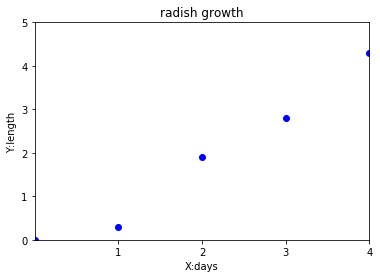
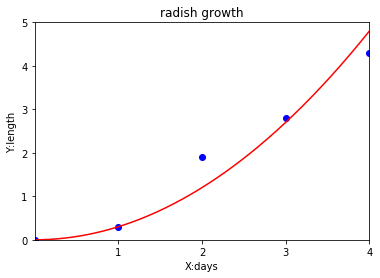
このデータをグラフにしました。
$x$軸が日数、$y$軸が葉っぱの長さです。

仮説の関数を1次関数とします。1次関数の方程式は

y = ax + b 

なので、$a$と$b$の値を何にすると、いい感じの関数となるかを算出します。
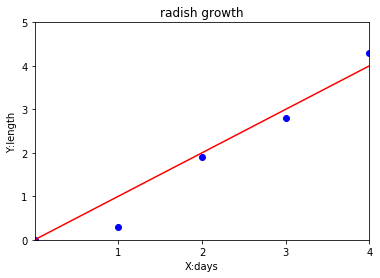
イメージとしては、赤いグラフのように、出来る限りデータにフィットする1次関数を求めます。

まず、仮説関数 $y = ax + b $ から ０～４ 日目 ( 日数は $x$ ) の $y$ の値を出して、実際の成長データとの誤差を出します。( 0日目は種を埋めた日 )

日数($x$)	０日目	１日目	２日目	３日目	４日目
記録	$0.0$cm	$0.3$cm	$1.9$cm	$2.8$cm	$4.3$cm
式から算出($y$)	$b$	$a+b$	$2a+b$	$3a+b$	$4a+b$
誤差($y-$記録)	$b-0$	$(a+b)-0.3$	$(2a+b)-1.9$	$(3a+b)-2.8$	$(4a+b)-4.3$

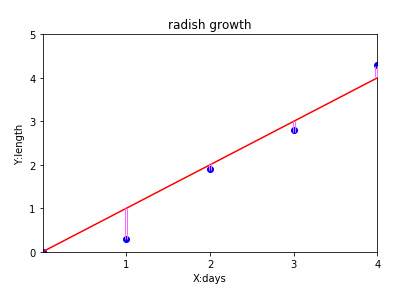
誤差は、下のグラフのピンクの部分の長さのことです。

誤差がマイナスにならないように、2乗してから合計します。
誤差の合計を$J$とすると、以下のような計算になります。

J = b^2+((a+b)-0.3)^2+((2a+b)-1.9)^2+((3a+b)-2.8)^2+((4a+b)-4.3)^2\\
\\
  =30a^2+20ab-59.4a+5b^2-18.6b+30.03

この$J$が最小となる$a$と$b$を求めれば、完了です。

$J$を$a$の関数として偏微分したものを0とし、$J$を$b$の関数として偏微分したものを0とし、2つの連立方程式を解けば、$J$が最小となるなる$a$と$b$が算出されます。

二変数二次元関数の最小値についてはこちらを参考に。
http://mathtrain.jp/quadratic

上の式が$a$で偏微分したもの($\frac{∂J}{∂a}$)、下の式が$b$で偏微分したもの($\frac{∂J}{∂b}$)です。

\left\{
\begin{array}{ll}
0 = 60a+20b-59.4 \\
0 = 20a+10b-18.6 
\end{array}
\right.

連立方程式を解くと、

\left\{
\begin{array}{ll}
a = 1.11 \\
b=-0.36
\end{array}
\right.

となり

y = 1.11x - 0.36 

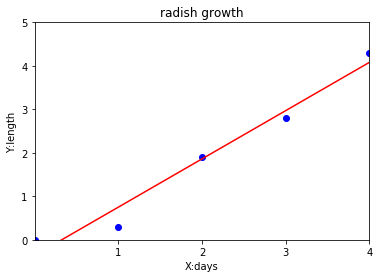
という関数を導き出せました。グラフで描画したら

とってもいい感じになりました!!

radish_plot.py

import matplotlib.pyplot as plt
import numpy as np
# data set
plt.plot([0,0.3,1.9,2.8,4.3], "bo") 

plt.title("radish growth")
plt.xlabel("X:days")
plt.ylabel("Y:length")
plt.xlim([0,4])
plt.xticks(np.arange(1,5,1))
plt.ylim([0,4])
plt.yticks(np.arange(0,6,1))

# Graph
x = np.arange(0,10,0.01)
y = 1.11*x -0.36
plt.plot(x,y,"r-")    
plt.show()              

一般式

具体例では、仮説の関数を一次関数としましたが、二次関数や三次関数の場合のほうがフィットすることもあるかもしれません。多分、普通はもっと複雑な関係式になるはずです。

はつか大根の例を二次関数にフィットさせると、

となり、こちらのほうがより良い式と考えられるかもしれません。
また、はつか大根の成長は日数だけでなく、日照時間や水の量にも影響を受けるかもしれません。

そのため、具体例を一般式に直して考えてみます。

葉っぱの長さを決定する要素として、日数と日照時間と与える水の量と $\cdots$ $n$ 個の要素があった場合、それぞれを$x_{1}$, $x_{2}$, $x_{3}$ $\cdots$ $x_{n}$とします。$x_{n}$の係数を$\theta_{n}$とします。

最終的に導き出したい関数、仮説関数は以下のような式で表わすことができます。
（$x_{1}$は$x$の1乗という意味ではなく、$x$に依存する関数です。最後のPythonコードを見るとわかりやすいかもです。）

h_{\theta}(x) = \theta_{0}x_{0} + \theta_{1}x_{1} + \theta_{2}x_{2} +\cdots + \theta_{n}x_{n}

$\theta_{0}$ は具体例の $b$ の部分で、$x_{0}=1$ として考えます。
急に、$h_{\theta}(x)$ が出てきましたが、具体例の $y$ で葉っぱの長さです。

具体例の関数 $y = 1.11x - 0.36 $ と上記の仮説関数を紐づけると以下のようになります。

$y$	$=$	$-0.36$	$×$	$1$	$+$	$1.11$	$×$	$x$
$h_{\theta}(x)$	$=$	$\theta_{0}$	$×$	$x_{0}$	$+$	$\theta_{1}$	$×$	$x_{1}$

この仮説関数に対して、サンプルデータが複数あり、以下のようなデータだとします。

$x_{0}$ (1固定)	$x_{1}$ (日数)	$x_{2}$ (日照時間h)	$x_{3}$ (水分量ml)	$\cdots$	$y$ (葉っぱの長さcm)
$1$	$1$	$14$	$150$	$\cdots$	$0.3$
$1$	$2$	$14$	$100$	$\cdots$	$1.9$
$1$	$3$	$14.1$	$160$	$\cdots$	$2.8$
$1$	$4$	$14.1$	$160$	$\cdots$	$4.3$

$i$ 行目の$j$ 列のデータを $x_{j}^{(i)}$, $y^{(i)}$ のように、表すことができ、マッピングさせるとこのような形です。
指数のように見えますが、データを示しているだけです。

$x_{0}$ (1固定)	$x_{1}$ (日数)	$x_{2}$ (日照時間h)	$x_{3}$ (水分量ml)	$\cdots$	$y$ (葉っぱの長さcm)
$x_{0}^{(1)}$	$x_{1}^{(1)}$	$x_{2}^{(1)}$	$x_{3}^{(1)}$	$\cdots$	$y^{(1)}$
$x_{0}^{(2)}$	$x_{1}^{(2)}$	$x_{2}^{(2)}$	$x_{3}^{(2)}$	$\cdots$	$y^{(2)}$
$x_{0}^{(3)}$	$x_{1}^{(3)}$	$x_{2}^{(3)}$	$x_{3}^{(3)}$	$\cdots$	$y^{(3)}$
$x_{0}^{(4)}$	$x_{1}^{(4)}$	$x_{2}^{(4)}$	$x_{3}^{(4)}$	$\cdots$	$y^{(4)}$

１列目のデータを$h_{\theta}(x)$に代入した場合、$h_{\theta}(x^{(1)})$と表します。

このような表し方をした場合、仮説関数との誤差の合計を以下のような関数に書き換えることができます。
$m$はデータセットの数です。上記の表の例だと4です。

J(\theta_{0},\theta_{1}, \cdots,\theta_{n})= \sum_{i=1}^{m} (h_{\theta}(x^{(i)})-y^{(i)})^2 

誤差の合計 $J(\theta_{0},\theta_{1}, \cdots,\theta_{n})$ が最小になる $\theta_{0}, \theta_{1}, \cdots,\theta_{n}$ のセットを導き出せばゴールです。

ここから、行列に置き換えて考えていきます。
行列はデータを一気に計算できるパワフルなアイテムです。

まずは、仮説関数 $h_{\theta}(x)$ を行列で表すために、$\theta_{0}$, $\theta_{1}$, $\cdots$ $\theta_{n}$と、$x_{0}$, $x_{1}$, $\cdots$ $x_{n}$を行列で表します。

\theta=\begin{bmatrix}
\theta_{0} \\
\theta_{1} \\
\vdots\\
\theta_{n} 
\end{bmatrix}
,
　　x=\begin{bmatrix}
x_{0} \\
x_{1} \\
\vdots\\
x_{n} 
\end{bmatrix}

このように置くと、$h_{\theta}(x)$ は $\theta$ の転置行列と行列 $x$ の積で表すことができます。

h_{\theta}(x)= \theta^T x\\

行列の転置と積ついては、こちらを参考に。
http://www.sist.ac.jp/~kanakubo/research/hosoku/trans_gyoretu.html

$i$ 列目のデータセット $x^{(i)}$ を行列で表し、全てのデータセットを与えた行列 $X$ を、各列の転置行列をセットしたもので表します。 $y^{(i)}$ も同様に行列で表します。

x^{(i)}=\begin{bmatrix}
x_{0}^{(i)} \\
x_{1}^{(i)} \\
\vdots\\
x_{n}^{(i)}
\end{bmatrix}
,　　
X=\begin{bmatrix}
(x^{(1)})^T \\
(x^{(2)})^T  \\
\vdots\\
(x^{(m)})^T 
\end{bmatrix}
=
\begin{bmatrix}
x_{0}^{(1)} & x_{1}^{(1)} & \cdots & x_{n}^{(1)} \\
x_{0}^{(2)} & x_{1}^{(2)} & \cdots & x_{n}^{(2)} \\
\vdots & \vdots & & \vdots\\
x_{0}^{(m)} & x_{1}^{(m)} & \cdots & x_{n}^{(m)} \\
\end{bmatrix}
,　　
y=\begin{bmatrix}
y^{(1)} \\
y^{(2)} \\
\vdots\\
y^{(m)}
\end{bmatrix}

ややこしく見えますが、上記の表をそのまま行列に直しただけです。

そして、話は一気に吹っ飛びます。

このように置いた場合、誤差の合計 $J(\theta)$ が最小になる $\theta$ は以下の行列式を解くことで求められます。

\theta =
(X^tX)^{-1}X^ty

なぜこの式になるかは、こちらを参考に。
http://mathtrain.jp/leastsquarematrix

また、$X^{-1}$は$X$の逆行列といい、こちらを参考に。
http://mathtrain.jp/inversematrix

この式にデータセットを入れて $\theta$ を求め、$h(\theta)$ の $\theta_{0}, \theta_{1}, \cdots,\theta_{n}$ に入れれば、最小二乗法による関数式(モデル関数)の完成です。

Pythonで書いてみた

この最小二乗法をPythonで書いてみました。
なんと、たった1行で $\theta$ が求められるんです！！

まずはデータセット。$y= 3+2\cos(x) + \frac{1}{2}x$ という関数に対して、誤差を発生させるため、乱数を加算します。

linalg_lstsq.py

x = arange(-3, 10, 0.1)
y = 3 + 2 * np.cos(x) + (1/2) * x + np.random.normal(0.0, 1.0, len(x)) 

一般式で説明した $x_{1}$ が $\cos(x)$、$x_{2}$ が $x$ です。
求める係数がそれぞれ $\theta_{0}$ が $3$、$\theta_{1}$ が $2$、$\theta_{2}$ が $\frac{1}{2}$ に近くなるよう計算できればOKです。

データセットをすべて設定した行列 $X$ を作ります。

linalg_lstsq.py

n = 3
X = np.zeros((len(x), n), float)
X[:,0] = 1
X[:,1] = np.cos(x)
X[:,2] = x

$\theta$ を求める式は、Numpyライブラリのlinalg.lstsqを使って、この一行。

linalg_lstsq.py

(theta, residuals, rank, s) = linalg.lstsq(X, y)

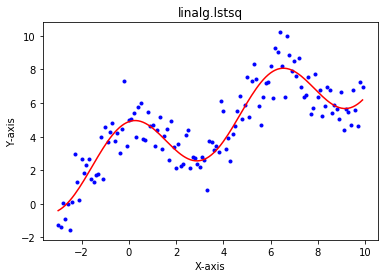
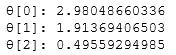
結果、こうなりました。

linalg_lstsq.py

import numpy as np
import matplotlib.pyplot as plt

# data-set
x = np.arange(-3, 10, 0.1)
y = 3 + 2 * np.cos(x) + (1/2) * x + np.random.normal(0.0, 1.0, len(x)) 

n = 3
X = np.zeros((len(x), n), float)
X[:,0] = 1
X[:,1] = np.cos(x)
X[:,2] = x

# Least square method
(theta, residuals, rank, s) = np.linalg.lstsq(X, y)

# data-set plot
plt.plot(x, y, 'b.')
# h(theta) plot
plt.plot(x, theta[0] + theta[1] * X[:,1] + theta[2] * X[:,2], 'r-')

plt.title("linalg.lstsq")
plt.xlabel("X-axis")
plt.ylabel("Y-axis")

plt.show()

print('θ[0]: %s' % theta[0])
print('θ[1]: %s' % theta[1])
print('θ[2]: %s' % theta[2])

かなり近い値が出せたし、グラフを見てもフィットしてますね！！

おわり

機械学習の勉強を始めたばかりなので、定番のアルゴリズム・考え方を学んでいるところです。特に真新しいことは書けませんが、誰かの役に立てれば嬉しいです。