以前の記事(Rでポイントパターン分析、Rでポイントパターン分析-分析エリアのマスキング)でspatstatパッケージを利用したマーク付点過程の分析を紹介しました。
この方法では、もともと分布そのものがもっている空間集積性(空間分布の偏り)の影響を排除することができないので、遺跡分布域を抽出して、それ以外の地域をマスクするという手法で望んだ結果を算出しました。
今回はsplancsパッケージにより、対象地域の一様性を仮定しない手法を紹介します。
ハチの目撃地点分布
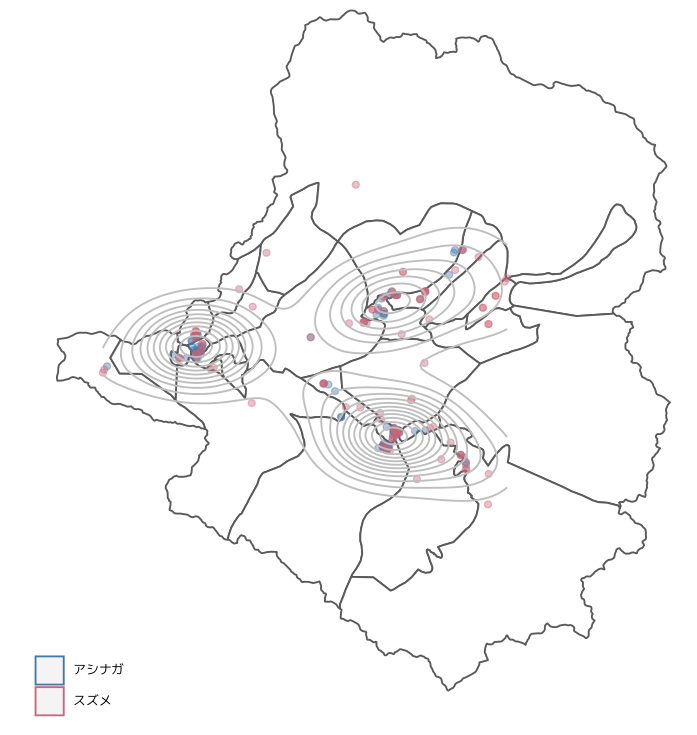
使用するデータは2017年と2018年のアシナガバチとスズメバチの目撃地点のデータです。sfパッケージでGISデータ(shpファイル)を読み込んで、ggplotで可視化します。
# パッケージ読み込み
library(tidyverse)
library(sf)
library(ggthemes)
library(spatstat)
library(splancs)
# 地図データ読み込み
data<-st_read(dsn="shp",layer="horne_point")
# 地図データ読み込み_厚沢部町字名
assabu<-st_read(dsn="shp",layer="assabu_area")
# 座標値を抜き出す
coord<-st_coordinates(data)%>%as.data.frame()
# 目撃位置マップ
p<-data%>%
filter(type=="スズメ" | type=="アシナガ")%>%
ggplot()+
geom_sf(data=assabu,fill="white")+
geom_sf(aes(colour=type),alpha=0.4)+
geom_density2d(data=coord,aes(X,Y),colour="grey")+
scale_colour_ptol()+
guides(size=FALSE)+
theme_map() +
theme(axis.title = element_blank(),
axis.text= element_blank(),
legend.title=element_blank())
print(p)
大きく3つのクラスターが確認できます。3つのクラスターは北海道厚沢部町の本町新町市街地、鶉地区、館地区に対応しています。
アシナガバチとスズメバチの空間集積性
spatstatパッケージを利用したカーネル密度推定図を作成します。
# pointをデータフレームに変換
point_df<-data%>%as.data.frame()
# ハチデータからxy座標を取り出す
coord<-st_coordinates(data)%>%as.data.frame()
# point_dfとcoordを結合
point_join<-bind_cols(point_df,coord)
# スズメとアシナガだけを選択
point_join2<-point_join%>%
filter(type=="スズメ" | type=="アシナガ")
# pppオブジェクトを作成
# c(),c()は分析対象領域のx座標とy座標の最小値、最大値
point_p<-ppp(point_join2$X,point_join2$Y,
c(point_join2$X%>%min(),point_join2$X%>%max()),
c(point_join2$Y%>%min(),point_join2$Y%>%max()),
marks=factor(point_join2$type))
# カーネル密度推定図
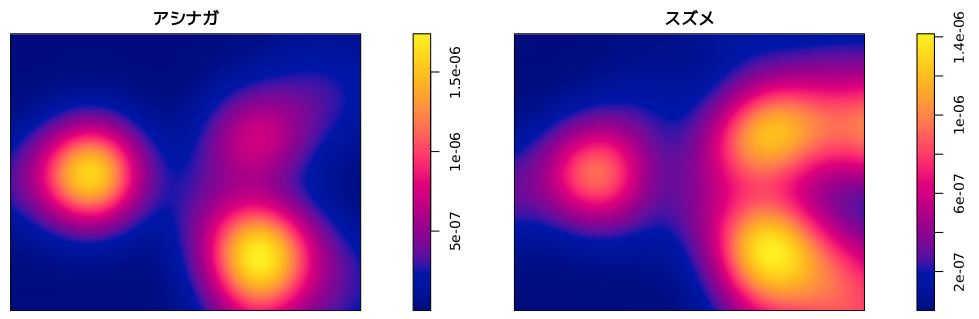
point_p%>%split()%>%density()%>%plot(1)
アシナガバチとスズメバチの分布はおおむね同じですが、スズメバチは3つの分布がほぼ同じ集積性を示すのに対して、アシナガバチでは右上(鶉地区)の集積性が低いようです。
splancsパッケージによる空間点過程
splancsパッケージのkhat()関数によりアシナガバチとスズメバチの分布(K統計量)と、その差分(アシナガK-スズメK=D(h))を繰り返し算出するモンテカルロ・シミュレーションを行います。モンテカルロ・シミュレーションはkenv.label()関数です。
# splancsパッケージでマーク付点過程
# ハチデータをデータフレームに変換
point_df<-data%>%as.data.frame()
# ハチデータからxy座標を取り出す
coord<-st_coordinates(data)%>%as.data.frame()
# point_dfとcoordを結合_大文字のXYを小文字にする
point_join<-bind_cols(point_df,coord)%>%
select(x = X,y=Y, everything())
# スズメバチだけを抽出
hor<-point_join%>%
filter(type=="スズメ")
# アシナガバチだけを抽出
bee<-point_join%>%
filter(type=="アシナガ")
# polyを算出
point_poly<-list(x=c(hor$x,bee$x),y=c(hor$y,bee$y))
# bboxを作成
point_bb<-bboxx(bbox(as.points(point_poly)))
# シミュレーションプロットのx軸を設定
# シミュレーション距離を10000mにして100mステップで分析
s<-seq(0,10000,100)
# khat関数適用
hor_hat<-khat(as.points(hor),point_bb,s)
bee_hat<-khat(as.points(bee),point_bb,s)
# k統計量の差分を算出
point_diff<-hor_hat-bee_hat
# エンベローブプロット描画
plot(s,point_diff,xlab="distance",ylab="D(h)",ylim=c(-8*10^7,8*10^7),type="l")
env_lab<-Kenv.label(as.points(hor),as.points(bee),point_bb,nsim=99,s=s)
lines(s,env_lab$upper,lty=2)
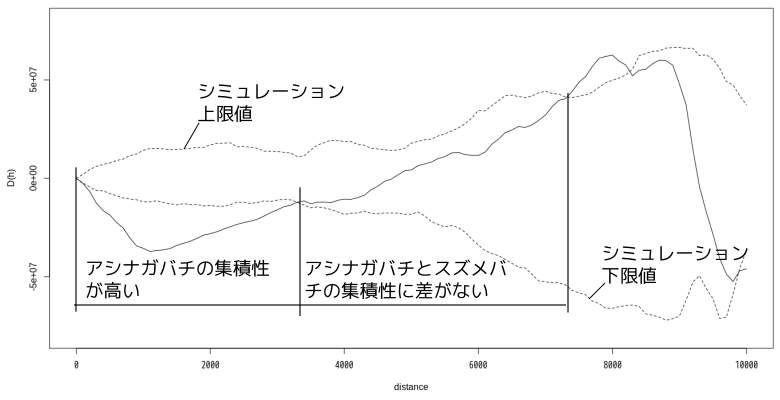
lines(s,env_lab$lower,lty=2)
点線は99回シミュレーションの上限値及び下限値、実線が推測値です。距離3,000m付近までは推測値が下限値を下回ることから、スズメバチに対してアシナガバチの空間集積性が高いことがわかります。3,000m以遠では空間集積性に差が見られなくなり、8,000m付近ではアシナガバチの空間集積性がむしろ低下します。
ハウスや農家納屋など住宅地以外でもその危険性から目撃情報が増えるスズメバチに対して、比較的危険が少なく、住宅地での目撃件数が多いアシナガバチは、3,000m以内の近距離レンジではスズメバチよりも集積性が高くなると思われます。3,000mを超えるレンジでは、住宅密集地と農地の距離を含みこんでしまうためか、集積性の差が目立たなくなっていきます。