クラスタリング（シルエット分析によるk-measn法のk設定）

はじめに

備忘録として書いてます。間違いや補足があればコメントいただけるとありがたいです。

クラスタリング

教師無し学習手法の一つ。データ間の距離（類似度）を元に、データをグループ化していく。
グループ化の手法自体もいくつもあり、いくつか列挙する。代表的な手法はk-means法。
k-means法についてはこちらが詳しい。
[k近傍法とk平均法の違いと詳細][1]

k-means法で問題になるのは分割するクラスタ数の設定。
これはハイパーパラメータとなっていて、よく分割できるクラスタ数をどうにか調べて設定する必要あり。

kの設定

今回参考にしたのは[Python機械学習プログラミング第2版][2]。
ここではkの設定としてエルボー法とシルエット分析を挙げている。
中でもシルエット分析を使ったkの設定を整理。
注意：自分の解釈が多分に含まれている。

(エルボー法は横軸にk、縦軸にクラスタ内誤差平方和をとり、グラフを書く方法で、急激にグラフが落ちる点でkを取るというもの。しかし、実際問題グラフが急激に落ちるなんでことはあまりなく、曲線が描かれるだけなのでこの中で「適切なk」を調べることになる。)

シルエット分析

シルエット分析ではクラスタ内のサンプルがどの程度密になっているか（凝集度）の目安となるグラフからkを設定する方法。

手順；大体は参考文献[2]を引用
①クラスタ内部のサンプルの凝集度$a^{(i)}$を計算。
N個のサンプルを持つクラスタＡのサンプル{$x^{(i)}|i \in A$}と同一クラスタの別のサンプル{$x^{(j)}|j \neq i,and,j \in A$}との平均距離として凝集度を計算する。
$a^{(i)}=\sum_{j=1}^{N}\frac{|x^{(i)}-x^{(j)}|}{N}$

②クラスタ同士の乖離度$b^{(i)}$を計算。
N個のサンプルを持つクラスタAのサンプル{$x^{(i)}|i \in A$}とM個のサンプルを持つクラスタBのサンプル{$x^{(m)}|i \in B$}との平均距離として乖離度を計算する。
$b^{(i)}=\sum_{m=1}^{M}\frac{|x^{(i)}-x^{(m)}|}{M}$

③クラスタの凝集度と乖離度の差を、それらの内大きい法で割り、シルエット係数を得る。
$s^{(i)}=\frac{b^{(i)}-a^{(i)}}{max[b^{(i)},a^{(i)}]}$

シルエット分析の実装というか引用

sklearnのsilhouette_samplesを使って実装すると次のようなコードになる。

#データセットの生成
from sklearn.datasets import make_blobs
X,y = make_blobs(n_samples=500, 
                 n_features=3,
                 centers=5,
                 cluster_std=0.5,
                 shuffle=True,
                 random_state=1
                )

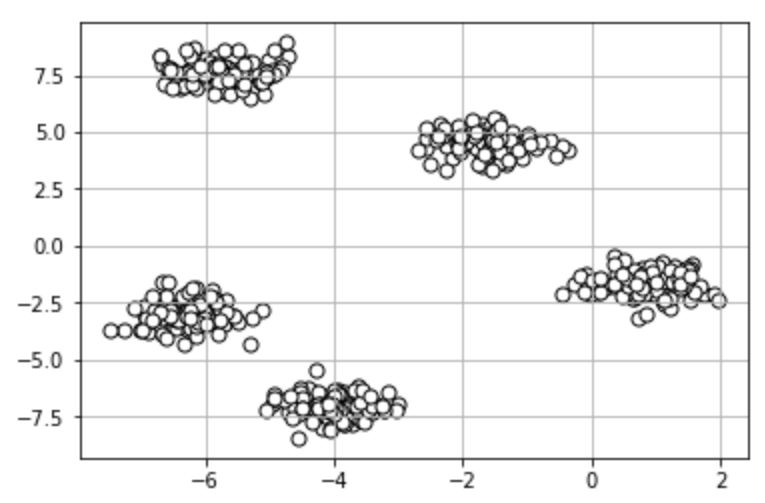
#データセットの可視化
import matplotlib.pyplot as plt
plt.scatter(X[:,0],X[:,1],c="w",marker="o",edgecolor="black",s=50)
plt.grid()
plt.show()

#k-means法
km=KMeans(n_clusters=5,
         init="k-means++",
         n_init=10,
         max_iter=300,
         random_state=0)
y_km=km.fit_predict(X)

import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples

cluster_labels=np.unique(y_km)
n_clusters=cluster_labels.shape[0]

#シルエット係数を計算
silhouette_vals=silhouette_samples(X,y_km,metric='euclidean')#ユークリッド距離
y_ax_lower,y_ax_upper=0,0
yticks=[]

for i,c in enumerate(cluster_labels):
  c_silhouette_vals=silhouette_vals[y_km==c]
  print(len(c_silhouette_vals))
  c_silhouette_vals.sort()
  y_ax_upper +=len(c_silhouette_vals)
  color=cm.jet(float(i)/n_clusters)
  plt.barh(range(y_ax_lower,y_ax_upper),
           c_silhouette_vals,
           height=1.0,
           edgecolor='none',
           color=color
          )
  yticks.append((y_ax_lower+y_ax_upper)/2.)
  y_ax_lower += len(c_silhouette_vals)
   
#シルエット係数が1であれば　良くクラスタリングできてる 
#またシルエットの幅がクラスタ数で平均して等しいとき、全体のデータを等分割できていることを示す
#この分割幅=シルエットバーの幅が等しくなり、かつ、シルエット係数が1に近づくようにkを最適化することが設定手法として考えられる.

#平均の位置に線を引く
silhouette_avg=np.mean(silhouette_vals)
plt.axvline(silhouette_avg,color="red",linestyle="--")
plt.ylabel("Cluster")
plt.xlabel("Silhouette coefficient")

結果
作成データ

シルエット図

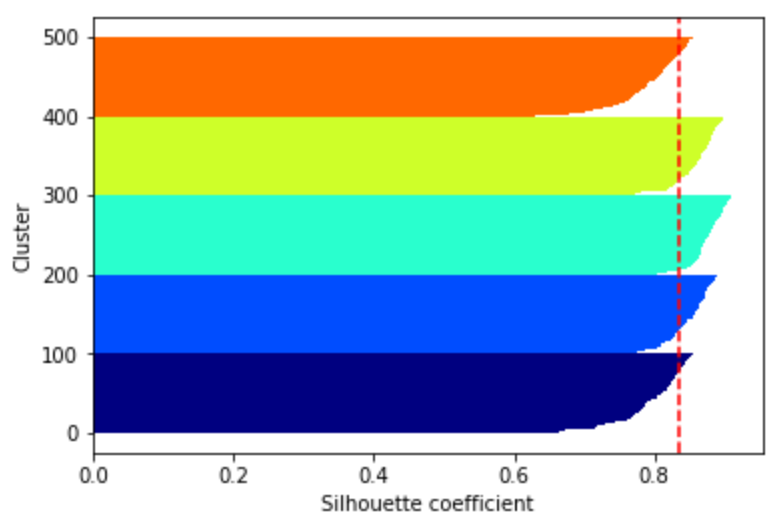
シルエット図は各バーの縦幅がクラスタ内のサンプル数、横軸自体がシルエット係数を表す。
シルエット係数が平均以上であるサンプルが多く、また各バーの縦幅が等しければ、同数の分割ができていることを表す。

つまり、kを変化させながら、シルエット図の各バーの縦幅が同じくらいになっているかどうかを確認し、同じくらいになっていれば均等に分割ができていることが分かる。

シルエット分析を回しながらkを探す

シルエット図の各バーの縦幅はクラスタ内のサンプル数であった。そこでkを変化させながら、k-means法によって分割されたクラスタのサンプル数を比較し、ある程度均等に分けられたときのkが最適なkであると判断するとしよう。

#シルエット分析をもとに最適なkを設定する
#データセットの生成
from sklearn.datasets import make_blobs
X,y = make_blobs(n_samples=500, 
                 n_features=3,
                 centers=5,
                 cluster_std=0.5,
                 shuffle=True,
                 random_state=1
                )

#データセットの可視化
import matplotlib.pyplot as plt
plt.scatter(X[:,0],X[:,1],c="w",marker="o",edgecolor="black",s=50)
plt.grid()
plt.show()

#クラスタリングの性能評価:シルエット分析
import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples

#kmeans関数
def kmeans(n_clust):
  km=KMeans(n_clusters=n_clust,
            init="k-means++",
            n_init=10,
            max_iter=300,
            random_state=0)
  y_km=km.fit_predict(X)
  return y_km

def n_label(y_km):
  cluster_labels=np.unique(y_km)
  n_clusters=cluster_labels.shape[0]
  return [cluster_labels,n_clusters]

#kを2～10まで探索
for i in range(2,10):
  y_km=kmeans(i)
  nn_l=n_label(y_km)
  cluster_labels=nn_l[0]
  n_clusters=nn_l[1]

  #シルエット係数を計算
  silhouette_vals=silhouette_samples(X,y_km,metric='euclidean')#ユークリッド距離

  sil=[]#クラスタ内のサンプル数を格納する配列
  for i,c in enumerate(cluster_labels):
    c_silhouette_vals=silhouette_vals[y_km==c]
    sil.append(len(c_silhouette_vals))
    
  #クラスタのサンプル数の差が10以下であればある程度分割できたとみなす
  if max(sil)-min(sil) < 10:
    print("    best of k:%d"%int(i+1),sil)
  else:
    print("not best of k:%d"%int(i+1),sil)

結果
作成データ

出力データ

このことから最も均等に分割できるk=5であることが分かった。
k=5と設定したときのシルエット図は前節のシルエット分析の紹介時に示したシルエット図である。

参考文献

[k近傍法とk平均法の違いと詳細][1]
[1]:https://qiita.com/NoriakiOshita/items/698056cb74819624461f#k%E5%B9%B3%E5%9D%87%E6%B3%95%E3%81%A8%E3%81%AF
[Python機械学習プログラミング第2版][2]
[2]:https://www.amazon.co.jp/Python-%E6%A9%9F%E6%A2%B0%E5%AD%A6%E7%BF%92%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%9F%E3%83%B3%E3%82%B0-%E9%81%94%E4%BA%BA%E3%83%87%E3%83%BC%E3%82%BF%E3%82%B5%E3%82%A4%E3%82%A8%E3%83%B3%E3%83%86%E3%82%A3%E3%82%B9%E3%83%88%E3%81%AB%E3%82%88%E3%82%8B%E7%90%86%E8%AB%96%E3%81%A8%E5%AE%9F%E8%B7%B5-impress-gear/dp/4295003379