この記事はFUJITSU Advent Calendar 2021の17日目です。
みんな大好きCOBOLの強みに十進演算があります。しかし、最近の言語には十進演算のための型(.NETのdecimalやJavaのjava.math.BigDecimalやその他)があるので、COBOL要らないんじゃない?みたいな話を聞いたりするわけです。それについて、COBOL処理系に関わっている身として思うところを述べたいと思います。「まあ、decimalやBigDecimalとかでできるっちゃできるんだけど…」の「だけど…」の部分を説明してみたい。
内容はざっと以下の通り。
- 二進浮動小数点で金計算をすると何がまずいかのおさらい。
- 十進浮動小数点の説明。
-
decimalやBigDecimalとCOBOL十進型の違い(BCDの説明)。 - で?
きっかけは、今年9月にとある記事のおかげでCOBOLがtwitterのトレンドに入った時のことです。その際に色々なtweetを目にして、十進演算が結構誤解されてるなあと感じました。十進演算がCOBOL固有のものだと思われていたり、十進とはBCDのことだと思われていたり。で、このあたりの説明を書きたいなあとぼんやり思ってたんですけど、せっかくなのでアドベントカレンダーに書くことにしました。
それにしても、ここしばらく、年に一回くらいなんやかんやでCOBOLがトレンドに入ってます。みなさんCOBOL大好きじゃないですか。
「浮動小数点型」変数に0.1を代入してみる
まず、「浮動小数点型」で金計算をすると何がまずいかをおさらいしましょう。
「浮動小数点型」変数が0.1というシンプルな小数値をちゃんと保持できるのか見てみます。ここで言う「浮動小数点型」は.NETやJavaなどでのfloat型やdouble型のことです。
手っ取り早くPowerShell Coreで試してみましょう。PowerShell Coreの中身は.NETなので、PowerShell Coreを通して.NETの動きを見てみます。
以下のサンプルを試す場合は、Windowsに元々インストールされている「Windows PowerShell」ではなく、PowerShell Coreを使ってください。Windows PowerShell(.NET Framework)では浮動小数点を文字列化する際の精度に制限があるようで、この後の説明の通りになりません。
- Microsoft Storeからインストールする場合: PowerShell
- コンテナを使う場合(Linuxイメージもあります): PowerShell
docker pull mcr.microsoft.com/powershellでイメージ取れます。
PowerShell Coreのコンソールを開いて、以下を実行してみます。
PS C:\> [double]$x = 0.1
変数xに0.1を代入してみました。[double]をつけることで、変数の型がdouble型(倍精度浮動小数点型)であることを明示しています。
xの値は何でしょうか?そりゃ0.1でしょう。だって、ほら。
PS C:\> $x
0.1
いや、それは罠です。doubleの仕様では、値を文字列化する場合16桁以降を丸めてしまうのがデフォルトなのです。20桁くらい表示させるようにしてみましょう。
PS C:\> $x.ToString("F20")
0.10000000000000000555
何かついてる。何もしてないのに誤差が出た!
というふうに、「浮動小数点型」は0.1というシンプルな小数ですら正確に保持できません。「浮動小数点を金計算に使ってはいけない」と言われる理由です。
なぜこんなことになるのか。
二進浮動小数点について
色々な言語でfloatやdoubleといった名前で用意されているデータ型は二進の浮動小数点です。浮動小数点には後で述べる十進とか他のもあるんだけど、「浮動小数点」といえばたいてい二進浮動小数点を指していますね。
二進浮動小数点型のデータは、「二進表記された小数」を保持していると考えるとよいでしょう。
十進表記の少数は、小数点以下1/10の位、1/100の位、...、1/10nの位、と続く数です。同様に、二進表記の少数は、小数点以下1/2の位、1/4の位、...、1/2nの位、と続く数です。例えば、二進表記で1.1は十進表記では1.5(1 + 1/2)ですし、二進表記の10.11は十進表記で2.75(2 + 0 + 1/2 + 1/4)です。
式で表すと、二進浮動小数点は、仮数sと指数eという二つの整数によって以下の形で表される数です。
s * 2-e
あるいは、分数で表現すれば以下のようになります。この記事では、以降こちらの形の表記を用います。
s / 2e
二進表記の1.1は (11)2 / 21だし、10.11は (1011)2 / 22です。ここで、(n)2はnが二進表記の数字であることを表しています。
実際の実装では、IEEE 754という規格に準拠しているものが多いです。例えば、.NETやJavaのdoubleはIEEE 754の倍精度(binary64)に準拠しています。この形式では、仮数部分から符号を独立させ、符号部、指数部、仮数部を以下のように64ビット中に割り当てています。
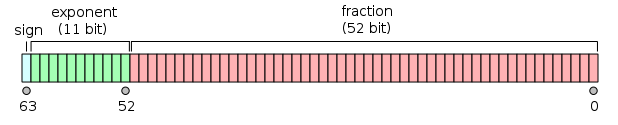
(出典: IEEE 754 Double Floating Point Format.svg)
この形式では、仮数部53ビット、指数部11ビットの範囲の値を表現することができます。上の割り当て図だと仮数部52ビット分しかないのになぜ53ビット表現できるかとか、指数部は特別な意味の値があるとか、正規化についてとか、詳細が気になる方はIEEE 754を見てみてください。
何が問題?
さて。二進浮動小数点型のデータは二進表記の小数を(仮数と指数が有効な範囲内であれば)正確に保持・計算することができます。例えば、二進表記で0.11(十進表記で0.75)という数をdouble型変数に代入してみましょう。
PS C:\> [double]$x = 0.75
PS C:\> $x.ToString("F40")
0.7500000000000000000000000000000000000000
40桁程出してみましたが、十進表記の0.1の時と異なり誤差は出ません。
一方、十進表記ではシンプルな表記となるのに、二進表記だと無限小数になってしまう数があります。というか、ほとんどの十進小数がそうです。0.1もその例です。
十進記法だと0.1というシンプルな値も、二進記法で表現すると無限小数になり、有限な桁数に収めようとすると丸めを行う必要があります。つまり、誤差が出てしまいます。
ところで、我々はもっぱら十進記法を使って生活しています。お金の帳簿も大昔から十進表記で記入したり計算したりしています。古代には十二進法とかで生活していた人もいたかもしれませんが、現在はほとんどの場面で十進記法を使いますね。
ということで、わしらが日常的に用いている十進記法の小数を計算機が得意な二進記法に変換しようとすると、ほぼ毎回誤差が発生するという困った状況になります。
これが金計算とかで二進浮動小数点を用いる場合の問題点です。「浮動小数点で十進計算すると誤差が出る」みたいにざっくりした言われ方されることがありますが、二進浮動小数点の加減乗算で(仮数と指数が有効な範囲内であれば)誤差は発生しません。除算や累乗根で丸めが必要になることはありますが、これは二進法に限ったことではありません(丸めの結果は進法によって異なりますが)。ここで問題になっている誤差は十進小数を二進小数に変換する際に発生しています。
なお、逆方向の二進小数から十進小数へは誤差なく変換することができます。都合のいいことに10は2を因数に持っているからです(二進小数 s / 2e は 十進小数 s * 5e / 10e に等しい)。0.1の例で見てみましょう。0.1をdouble型変数に代入すると、二進の無限小数が丸められて53ビット仮数として保持されます。その値を十進表記で見てみます。上の式からすると、53桁前後で表現できそうに思えます。正規化の都合上、正確に53桁になるとは限りませんが...
PS C:\> [double]$x = 0.1
PS C:\> $x.ToString("F70")
0.1000000000000000055511151231257827021181583404541015625000000000000000
70桁表示させてみると、小数点以下55桁より後は0が続いています。ちなみに、上の変換式から分かるように、二進小数を十進小数に変換した場合、小数点以下の(0でない)最後の桁は必ず5になります。
十進数が広く使われているのは、人間の両手の指が10本だからだと言われています。指が片手8本両手16本となるように人類が進化して、十六進小数を使って帳簿をつけるようになっていたら、計算機と非常に相性が良かったでしょうが、まあ、仕方ないね。
十進浮動小数点について
わしらはもっぱら十進表記の小数で帳簿つけたりしているんだから、十進表記のまま計算できればええんちゃうの?ということで、十進浮動小数点型です。いや、COBOLは昔からやってましたけど。
十進浮動小数点は、原理的には、仮数sと指数eという二つの整数を用いて、以下の形の数を扱います。
s / 10e
(比較)二進浮動小数点: s / 2e
例えば、123.45 は 12345 / 102 という形で扱います。十進浮動小数点型データは、十進表記された小数を(仮数と指数が有効な範囲内であれば)正確に保持・計算することができます。
.NETだとdecimal型、Javaだとjava.math.BigDecimalクラスがこれに相当します。
前述の0.1を変数に格納する例をdecimal型を使ってやってみましょう。
PS C:\> [decimal]$x = 0.1
PS C:\> $x.ToString("F40")
0.1000000000000000000000000000000000000000
40桁出してみても、誤差は出ませんね。
やったー。じゃあ、二進浮動小数点やめて全部十進浮動小数点にすればいいんじゃね?
いや、さすがにそれは。計算機にとっては二進浮動小数点の方が扱いやすくて計算が速いので、誤差をコントロールしつつがしがし計算するには二進浮動小数点だと思います。
なお、上記の規格IEEE 754には、2008年版以降、十進浮動小数点に関する規格も追加されています。十進浮動小数点の扱いも今後IEEE 754準拠のものが増えていくんじゃないでしょうか。
BCDについて
十進浮動小数点はCOBOLでも多用されます。COBOLのそれらとdecimalやBigDecimalは数を表す原理は一緒です。しかし、内部表現に重要な違いがあります。
十進浮動小数点は、以下の形の数でした。
s / 10e
decimalやBigDecimalでは、ここのsという整数(仮数)を内部では二進形式で保持しています。つまり、
12345 / 102 (= 123.45)
という数の場合、12345という整数値は11000000111001という形(十六進で3039)で保持されています。
実際には、decimalは仮数部をlongとintの組み合わせで96-bit整数として実装していますし、BigDecimalは仮数部としてBigIntegerを用いています。が、論理上は仮数は二進形式で保持されていると考えてよいでしょう。
一方、COBOLの十進形式では、仮数部はBCD(二進化十進)と呼ばれる形式で表現されています。
上の 12345 / 102 の例だと、仮数部(12345)を表現するには(最低)5バイト必要であり、各バイトの中身は十六進表記で例えば以下のようになります。
31, 32, 33, 34, 35
ちなみに、これをASCII文字列とみなせば、"12345"となります。
これがBCD「ゾーン形式」と呼ばれる表現形式です。1バイトで十進数字の1桁を表現します。正確には、「ゾーンビット(各バイトの上位4ビット)」の種類や、符号をどう表現するかでいくつかの流儀がありますが、基本的な考え方は上の通り。
5桁の数値を表すのに5バイト消費するのはかなりぜいたくです。なので、「パック形式」と呼ばれるもう少し効率的な形式もあります。この形式だと、12345を表現するために(最低)3バイト必要で、各バイトの中身は十六進表記で以下のようになります。
12, 34, 5C
4ビットで十進数字の1桁を表現します。最後の4ビットは符号を表す特別な「桁」になります。
(2012年2月19日追記)
すいません、上の例の符号を表す「桁」部分について、FからCに修正しています。
符号なしの場合のFとなるのですが、この流れでは符号付の値とみなすのが自然なので、Cの方が適切でした。
(追記ここまで)
BCDの利点は?
今となってはBCD表現の利点はほとんどないように見えます。メモリ効率悪いし、計算遅そうだし。メインフレームではBCDの計算にハードウェア支援があったと聞きますが、今時のCPUではソフトウェア的に頑張る必要があります。実を言うとx86にもBCD支援命令があるにはあるんですが、あまり便利なものではありません。ほとんど使われていないんじゃないかな。少なくとも富士通のNetCOBOLでは使っていない。ということで、コンパイラが頑張ってコード生成しています。
じゃあ、BCDはまったくいいところなしなのかと言えば、そういうわけでもなく、二進表現よりも有利な点があるにはあります。
桁揃えが速い
浮動小数点どうしを加減算する場合、桁をそろえる必要があります。
例えば、123.45 + 6.789は十進浮動小数点としては以下のように桁をそろえて(指数部分を揃えて)計算することになります。
12345 / 102 + 6789 / 103
= (12345 * 10) / 103 + 6789 / 103
= (123450 + 6789) / 103
加算という単純な計算のはずなのに、「仮数を10倍する」という乗算が発生しています。(二行目)
仮数が二進表現の場合、実際に乗算しなければならず、コストのかかる計算になります。一方、仮数がBCDだとデータを8ビットまたは4ビットシフトする比較的単純な操作になります。
丸めが速い
例えば、「小数点第三位を四捨五入して小数点第二位までに丸める」という操作を考えます。
小数点第三位の桁の数字を得るためには、仮数が二進表現の場合、10n で割ったり剰余を取ったりして計算する必要があります。コストのかかる計算です。一方、仮数がBCDの場合、小数点位置から3桁目に相当する「箱」の中身を取り出すだけで済みます。
で?
どっちがいいの?
decimalでもBigIntegerでもBCDでも、(仮数と指数が有効な範囲内であれば)十進表記された数を正確に保持・計算することができます。速さについては、今時のCPUではBCDが不利でしょう。丸めが速いと言っても全体的には計算に手がかかる。ただ、COBOLが扱うようなタスクだと、計算処理よりIOとかの方がはるかに重いので、BCDかどうかの差が顕在化するようなことはあまり無いとは思いますが。
ということで、どっちも大丈夫。どちらでも問題なく十進計算できます。
心配事は全然別の点にあります。「このCOBOLの処理をJavaで書き直して。完全互換で」みたいな話がたくさん出てくるんじゃないか。BigInteger使えばできるんでしょ?まあ、できるっちゃできるんだけど…
例えば。COBOLは十進浮動小数点の考え方で十進演算を行いますが、実際のCOBOLのデータは浮動小数点ではなく固定小数点です。つまり、変数の定義に「小数点以下2桁まで」とかの宣言が入ってます。従って、変数に値を格納する際には丸めが発生します。
そのため、COBOLの計算処理には、いたるところに暗黙の丸めが発生しています。
以下の単純なCOBOLプログラムを考えます。十進小数に掛け算と足し算をするだけのものです。計算の入力は小数点3桁ですが、結果は2桁に切り捨てています。
PROGRAM-ID. MAIN.
DATA DIVISION.
WORKING-STORAGE SECTION.
77 WK-VAL1 PACKED-DECIMAL PIC 99V999 VALUE 9.009.
77 WK-VAL2 PACKED-DECIMAL PIC 99V999 VALUE 0.999.
77 WK-VAL3 PACKED-DECIMAL PIC 99V999 VALUE 0.001.
77 WK-RESULT PACKED-DECIMAL PIC 99V99.
77 WK-FORMAT PIC Z9.99.
PROCEDURE DIVISION.
* 計算を行う
MULTIPLY WK-VAL1 BY WK-VAL2 GIVING WK-RESULT.
ADD WK-VAL3 TO WK-RESULT.
* 結果を表示する
* 8.99が表示されるはず
MOVE WK-RESULT TO WK-FORMAT.
DISPLAY WK-FORMAT.
END PROGRAM MAIN.
これを忠実にC#に移植すると以下のようになります。
class Sample {
static void Main(string[] args) {
// 元ソースと比較のため、入力データは変数として用意しておく
decimal val1 = 9.009m;
decimal val2 = 0.999m;
decimal val3 = 0.001m;
// 計算を行う
decimal temp = decimal.Round(val1 * val2, 2, MidpointRounding.ToZero);
decimal result = decimal.Round(temp + val3, 2, MidpointRounding.ToZero);
// 結果を表示する
// 8.99が表示されるはず(丸めが無かったら9.00になる)
Console.WriteLine(result);
}
}
表面上見えていなかった丸めをちゃんと入れています。Javaになるともっと複雑になります。
import java.math.*;
public class Sample {
public static void main(String[] args) {
// 元ソースと比較のため、入力データは変数として用意しておく
BigDecimal val1 = new BigDecimal("9.009");
BigDecimal val2 = new BigDecimal("0.999");
BigDecimal val3 = new BigDecimal("0.001");
// 計算を行う
MathContext mc;
// 繰り上がりが発生する場合があるので、
// val1.multiply(val2, mc)とはできない。
BigDecimal temp = val1.multiply(val2);
mc = new MathContext(temp.precision() - temp.scale() + 2, RoundingMode.DOWN);
temp = temp.round(mc);
temp = temp.add(val3);
mc = new MathContext(temp.precision() - temp.scale() + 2, RoundingMode.DOWN);
BigDecimal result = temp.round(mc);
// 結果を表示する
// 8.99が表示されるはず(丸めが無かったら9.00になる)
System.out.println(result);
}
}
Javaの場合、有効桁数的な考え方で丸めを行うので、「小数点以下2桁で切り捨て」のような処理は少し面倒になります。
(2022年1月6日追記)
すいません、BigDecimalにも「小数点以下2桁で切り捨て」のような処理を行うメソッド(setScale)がありました。丸め処理を書く必要はありますが、メソッド呼び出しひとつで書けます。詳細は @mazeneko さんの2022-01-06 01:29のコメントをご覧ください。
(追記ここまで)
これはきわめて単純な例ですが、COBOLプログラムを忠実に移植するとなると、COBOLの計算の癖を丁寧に拾って再現させていかなければなりません。読みづらいし、なぜこうしなければならないか説明しづらいソースになります。仕様を当世風に合わせて再定義できればいいんですけど、「動きが変わると困る」とか言われてしまうと大変ですね。
でも、不可能ではないんだろう?
メモリ4GのPCを支給して「不可能ではないんだろう?」みたいなことをおっしゃいますね。『技術的には可能です』が、用途に適した道具を使った方が楽なんじゃないでしょうか。
ということで、「今時の言語で十分に十進プログラミングはできます。ただ、今COBOLで動いているプログラムを仕様そのままに実装するなら、COBOLで書いた方が素直な記述になることが多いですよ」というのがわたくしの思うところでございます。
おわりに
今後ともCOBOLをよろしくお願い申し上げます。