目的
JAGURSという津波シミュレーションを行うためのデータ作り。
内閣府中央防災会議が謎の緯度経度座標系を使ってくれて扱いにすごく悩んだのでここに記します。
誰かの役に立てばいいね!
そして、僕が約15年前に作った座標変換プログラムのメモ帳です。
(正確には、今はなき緯度経度変換ページのJavaScriptをfortran化させたものです)
データの入手等はぼくが前に書いた記事を見てください。
UTM座標系
UTMとは、wikipedia先生の ユニバーサル横メルカトル図法を見てください。
ひらたく言うと、地球は丸いけど、二次元平面に投影しますよ、というやつです。
日本近海の津波のシミュレーションをやる場合は直交座標系で十分です(たぶん
日本の緯度経度座標系
旧測地系と呼ばれるものと、世界測地系と呼ばれるものが混在してるので気をつけましょう。
特に日本では旧測地系と呼ばれるものが、未だに大活躍しています。
中央防災会議が使った謎の測地系
ちなみにG空間情報センターからダウンロードできる津波計算用のデータで、南海トラフはUTM53なので一般的に公開されているソフトやライブラリで対応できますが、東北用が謎です。
公式ドキュメントのスクショを以下に示します。

僕には「データの作成にあたっては、中心軽度を143度とするUTM座標系を投影法として使用した。東西方向の原点の値は500,000mとした。」という日本語が僕にとってはまじで意味不明でした。
緯度経度 UTM 相互変換プログラム
ちなみに測地系の違いについて、僕は全く理解していません。
このプログラムの正しさについては、いろんな変換サイトで同じ結果が出ることを確認しただけですので、動作を保証するものではありません。
現代では、これを実現するライブラリがPythonなどでは公開されているのでそちらを利用することを強くお勧めします。
使い方 wgs2utm53(y,x,id,kd) y:南北 x:東西 id:緯度 kd:軽度 (なぜかUTMの世界ではxは南北方向らしいので注意)
!**************************************
subroutine tokyo2wgs(bw,lw,bt,lt)
implicit none
real(kind=8) bt,lt
real(kind=8) bw,lw
real(kind=8) ht,hw
real(kind=8) aw,fw,e2w
real(kind=8) at,ft,e2t
real(kind=8) dx,dy,dz
real(kind=8) x,y,z
ht =0.d0
aw = 6378137.d0
fw = 1 / 298.257223d0
e2w = 2d0*fw - fw*fw
at = 6377397.155d0
ft = 1.d0 / 299.152813d0
e2t = 2.d0*ft - ft*ft
dx = -148.d0
dy = 507.d0
dz = 681.d0
call llh2xyz(x,y,z,bt,lt,ht,at,e2t)
call xyz2llh(bw,lw,hw,x+dx,y+dy,z+dz,aw,e2w)
return
end
!***********************************************
!***********************************************
subroutine tokyo2utm(x,y,b,l)
implicit none
real(kind=8) b,l
real(kind=8) x,y
real(kind=8) rd
integer zn
real(kind=8) l0
real(kind=8) a,f,e2
rd =3.14159265358979323846264338327950288419716939937d0/180.d0
a = 6377397.155d0
f = 1d0 / 299.152813d0
e2=2.0d0*f-f*f
zn = mod(int((l+180.d0)/6.d0),60)+1
l0=dble(zn)*6.d0-183.d0 !原点だそうだ。
!write(*,*) '中央罫線:東経',l0
call ll2xy(x,y,b*rd,(l-l0)*rd,a,f,e2)
x = x*0.9996d0
y = y*0.9996d0
y = y+500000.d0
return
end
!***********************************************
!***********************************************
subroutine wgs2utm(x,y,b,l)
implicit none
real(kind=8) b,l
real(kind=8) x,y
real(kind=8) rd
integer zn
real(kind=8) l0
real(kind=8) a,f,e2
rd =3.14159265358979323846264338327950288419716939937d0/180.d0
a=6378137.d0
f=1.0d0/298.257223d0
e2=2.0d0*f-f*f
zn = mod(int((l+180.d0)/6.d0),60)+1
l0=dble(zn)*6.d0-183.d0 !原点だそうだ。
!write(*,*) '中央罫線:東経',l0
call ll2xy(x,y,b*rd,(l-l0)*rd,a,f,e2)
x = x*0.9996d0
y = y*0.9996d0
y = y+500000.d0
return
end
!***********************************************
!***********************************************
subroutine wgs2utm53(x,y,b,l)
implicit none
real(kind=8) b,l
real(kind=8) x,y
real(kind=8) rd
integer zn
real(kind=8) l0
real(kind=8) a,f,e2
rd =3.14159265358979323846264338327950288419716939937d0/180.d0
a=6378137.d0
f=1.0d0/298.257223d0
e2=2.0d0*f-f*f
zn = 53 !mod(int((l+180.d0)/6.d0),60)+1
l0=dble(zn)*6.d0-183.d0 !原点だそうだ。
!write(*,*) '中央罫線:東経',l0
call ll2xy(x,y,b*rd,(l-l0)*rd,a,f,e2)
x = x*0.9996d0
y = y*0.9996d0
y = y+500000.d0
return
end
!***********************************************
!**************************************************
subroutine utm2wgs(b,l,x,y,zn)
implicit none
real(kind=8),intent(out):: b,l
real(kind=8),intent(in)::x,y
integer,intent(in) :: zn
real(kind=8) :: a,f,e2,ed2,e4,e6,e8
real(kind=8) :: cad,cbd,ccd,cdd,ced
real(kind=8) :: l0,eps,m0,cb,eta2,rn
real(kind=8) :: xd,yd,tx,ty
real(kind=8) :: db,dl
real(kind=8) :: rd
rd =3.14159265358979323846264338327950288419716939937d0/180.d0
a = 6378137.d0! # 赤道半径 (WGS 84)
f = 1.d0 / 298.257223d0 ! # 扁平率 (WGS 84)
e2 = 2.d0*f - f*f !; # 第1離心率
ed2 = e2 / (1.d0-e2)!; # 第2離心率
e4 = e2 * e2
e6 = e4 * e2
e8 = e6 * e2
cad=a*(1.d0-e2)*(1.d0+3.d0/4.d0*e2+45.d0/64.d0*e4
& +175.d0/256.d0*e6+11025.d0/16384.d0*e8)
cbd=a*(1.d0-e2)*( 3.d0/4.d0*e2+15.d0/16.d0*e4
& +525.d0/512.d0*e6+ 2205.d0/2048.d0*e8)
ccd=a*(1.d0-e2)*( 15.d0/64.d0*e4
& +105.d0/256.d0*e6+ 2205.d0/4096.d0*e8)
cdd=a*(1.d0-e2)*(
& 35.d0/512.d0*e6+ 315.d0/2048.d0*e8)
ced=a*(1.d0-e2)*(
& 315.d0/16384.d0*e8)
l0 = dble(zn)*6.d0-183.d0
eps = 0.0000001d0/3600.d0*rd
m0 = 0.9996d0
ty = y-500000.d0
tx = x/m0
ty = ty/m0
db = 1.d0
dl = 1.d0
b = tx/cad
cb = dcos(b)
eta2 = ed2*cb*cb
rn = a/(1.d0-f)/dsqrt(1.d0+eta2)
l=ty/rn/cb
do while(db>eps .or. dl>eps)
call ll2xy(xd,yd,b,l,a,f,e2)
db = (tx-xd)/cad
cb = dcos(b)
eta2=ed2*cb*cb
rn = a/(1.d0-f)/dsqrt(1.d0+eta2)
dl = (ty-yd)/rn/cb
b = b+db
l = l+dl
end do
b = b/rd
l = l/rd+l0
end subroutine utm2wgs
!****************************************************
!**************************************************
subroutine utm2tokyo(b,l,x,y,zn)
implicit none
real(kind=8),intent(out):: b,l
real(kind=8),intent(in)::x,y
integer,intent(in) :: zn
real(kind=8) :: a,f,e2,ed2,e4,e6,e8
real(kind=8) :: cad,cbd,ccd,cdd,ced
real(kind=8) :: l0,eps,m0,cb,eta2,rn
real(kind=8) :: xd,yd,tx,ty
real(kind=8) :: db,dl
real(kind=8) :: rd
rd =3.14159265358979323846264338327950288419716939937d0/180.d0
!a = 6378137.d0! # 赤道半径 (WGS 84)
!f = 1.d0 / 298.257223d0 ! # 扁平率 (WGS 84)
a = 6377397.155d0 !; # 赤道半径 (Tokyo)
f = 1.d0 / 299.152813d0 !; # 扁平率 (Tokyo)
e2 = 2.d0*f - f*f !; # 第1離心率
ed2 = e2 / (1.d0-e2)!; # 第2離心率
e4 = e2 * e2
e6 = e4 * e2
e8 = e6 * e2
cad=a*(1.d0-e2)*(1.d0+3.d0/4.d0*e2+45.d0/64.d0*e4
& +175.d0/256.d0*e6+11025.d0/16384.d0*e8)
cbd=a*(1.d0-e2)*( 3.d0/4.d0*e2+15.d0/16.d0*e4
& +525.d0/512.d0*e6+ 2205.d0/2048.d0*e8)
ccd=a*(1.d0-e2)*( 15.d0/64.d0*e4
& +105.d0/256.d0*e6+ 2205.d0/4096.d0*e8)
cdd=a*(1.d0-e2)*(
& 35.d0/512.d0*e6+ 315.d0/2048.d0*e8)
ced=a*(1.d0-e2)*(
& 315.d0/16384.d0*e8)
l0 = dble(zn)*6.d0-183.d0
eps = 0.0001d0/3600.d0*rd
m0 = 0.9996d0
ty = y-500000.d0
tx = x/m0
ty = ty/m0
db = 1.d0
dl = 1.d0
b = tx/cad
cb = dcos(b)
eta2 = ed2*cb*cb
rn = a/(1.d0-f)/dsqrt(1.d0+eta2)
l=ty/rn/cb
do while(db>eps .or. dl>eps)
call ll2xy(xd,yd,b,l,a,f,e2)
db = (tx-xd)/cad
cb = dcos(b)
eta2=ed2*cb*cb
rn = a/(1.d0-f)/dsqrt(1.d0+eta2)
dl = (ty-yd)/rn/cb
b = b+db
l = l+dl
end do
b = b/rd
l = l/rd+l0
end subroutine utm2tokyo
!****************************************************
!***********************************************
subroutine ll2xy(x,y,b,dl,a,f,e2)
implicit none
real(kind=8) x,y
real(kind=8) b,dl
real(kind=8) a,f,e2
real(kind=8) dl2,dl4
real(kind=8) sb,cb,cb3,cb5,tb2,tb4,ed2,eta2,rn
real(kind=8) lom
x=0.d0
y=0.d0
dl2=dl**2
dl4=dl**4
sb=dsin(b)
cb=dcos(b)
cb3 = cb*cb*cb
cb5 = cb3*cb*cb
tb2 = sb*sb/cb/cb
tb4 = tb2*tb2
ed2=e2/(1.d0-e2)
eta2 = ed2*cb*cb
rn=a/(1.d0-f)/dsqrt(1.d0+eta2)
x=lom(b,a,f,e2)
!write(*,*) '赤道からの距離:',nint(x)/1000.d0
x =x+ rn/2.d0*sb*cb*dl2
x =x+ rn/24.d0*sb*cb3*(5.d0-tb2+9.d0*eta2+4.d0*eta2*eta2)*dl4
x =x+ rn/720.d0*sb*cb5*(61.d0-58.d0*tb2+tb4)*dl4*dl2
y = rn*cb*dl
y =y+ rn/6.d0*cb3*(1.d0-tb2+eta2)*dl*dl2
y =y+ rn/120.d0*cb5*(5.d0-18.d0*tb2+tb4)*dl*dl4
return
end
!*****************************************************
!*****************************************************
function lom(b,a,f,e2)
implicit none
real(kind=8) lom
real(kind=8) b,a,f,e2
real(kind=8) e4,e6,e8
real(kind=8) cad,cbd,ccd,cdd,ced
e4=e2*e2
e6=e4*e2
e8=e6*e2
cad=a*(1.d0-e2)*(1.d0+3.d0/4.d0*e2+45.d0/64.d0*e4
& +175.d0/256.d0*e6+11025.d0/16384.d0*e8)
cbd=a*(1.d0-e2)*( 3.d0/4.d0*e2+15.d0/16.d0*e4
& +525.d0/512.d0*e6+ 2205.d0/2048.d0*e8)
ccd=a*(1.d0-e2)*( 15.d0/64.d0*e4
& +105.d0/256.d0*e6+ 2205.d0/4096.d0*e8)
cdd=a*(1.d0-e2)*(
& 35.d0/512.d0*e6+ 315.d0/2048.d0*e8)
ced=a*(1.d0-e2)*(
& 315.d0/16384.d0*e8)
lom= cad*b-cbd/2.d0*dsin(2.d0*b)+ccd/4.d0*dsin(4.d0*b)
& -cdd/6.d0*dsin(6.d0*b)+ced/8.d0*dsin(8.d0*b)
return
end
!***************************************************
!*****************************************************
subroutine llh2xyz(x,y,z,b,l,h,a,e2)
implicit none
real(kind=8) x,y,z
real(kind=8) b,l,h,a,e2
real(kind=8) br,lr,sb,cb,rn
real(kind=8) rd
rd =3.14159265358979323846264338327950288419716939937d0/180.d0
br = b*rd
lr = l*rd
sb = dsin(br)
cb = dcos(br)
rn = a/dsqrt(1.d0-e2*sb*sb)
x = (rn+h) * cb * dcos(lr)
y = (rn+h) * cb * dsin(lr)
z = (rn*(1.d0-e2)+h) * sb
!write(*,*)e2
end
!***************************************************
!*************************************************
subroutine xyz2llh(b,l,h,x,y,z,a,e2)
implicit none
real(kind=8) x,y,z,a,e2
real(kind=8) b,l,h
real(kind=8) bda,p,t,st,ct,sb,rn
real(kind=8) rd
rd =3.14159265358979323846264338327950288419716939937d0/180.d0
bda = dsqrt(1.d0-e2)
p = dsqrt(x**2+y**2)
t = datan2(z, p*bda)
st = dsin(t)
ct = dcos(t)
b = datan2(z+e2*a/bda*st**3, p-e2*a*ct**3)
l = datan2(y, x)
sb = dsin(b)
rn = a / dsqrt(1.d0-e2*sb*sb)
h = p/dcos(b) - rn
b = b/rd
l = l/rd
end
!******************************************************
なぞの座標系への対応
「データの作成にあたっては、中心軽度を143度とするUTM座標系を投影法として使用した。東西方向の原点の値は500,000mとした。」
とのころなので、プログラム中のl0を143にして出てきた東西方向の値から500000引いたらいいんやろなぁと思いました。
ので以下のサブルーチンを作りました。
!**************************************************
subroutine utm2wgs_nazo(b,l,x,y,zn)
implicit none
real(kind=8),intent(out):: b,l
real(kind=8),intent(in)::x,y
integer,intent(in) :: zn
real(kind=8) :: a,f,e2,ed2,e4,e6,e8
real(kind=8) :: cad,cbd,ccd,cdd,ced
real(kind=8) :: l0,eps,m0,cb,eta2,rn
real(kind=8) :: xd,yd,tx,ty
real(kind=8) :: db,dl
real(kind=8) :: rd
rd =3.14159265358979323846264338327950288419716939937d0/180.d0
a = 6378137.d0! # 赤道半径 (WGS 84)
f = 1.d0 / 298.257223d0 ! # 扁平率 (WGS 84)
e2 = 2.d0*f - f*f !; # 第1離心率
ed2 = e2 / (1.d0-e2)!; # 第2離心率
e4 = e2 * e2
e6 = e4 * e2
e8 = e6 * e2
cad=a*(1.d0-e2)*(1.d0+3.d0/4.d0*e2+45.d0/64.d0*e4
& +175.d0/256.d0*e6+11025.d0/16384.d0*e8)
cbd=a*(1.d0-e2)*( 3.d0/4.d0*e2+15.d0/16.d0*e4
& +525.d0/512.d0*e6+ 2205.d0/2048.d0*e8)
ccd=a*(1.d0-e2)*( 15.d0/64.d0*e4
& +105.d0/256.d0*e6+ 2205.d0/4096.d0*e8)
cdd=a*(1.d0-e2)*(
& 35.d0/512.d0*e6+ 315.d0/2048.d0*e8)
ced=a*(1.d0-e2)*(
& 315.d0/16384.d0*e8)
l0 =143.d0 !dble(zn)*6.d0-183.d0
eps = 0.0000001d0/3600.d0*rd
m0 = 0.9996d0
ty = y -500000.d0
tx = x/m0
ty = ty/m0
db = 1.d0
dl = 1.d0
b = tx/cad
cb = dcos(b)
eta2 = ed2*cb*cb
rn = a/(1.d0-f)/dsqrt(1.d0+eta2)
l=ty/rn/cb
do while(db>eps .or. dl>eps)
call ll2xy(xd,yd,b,l,a,f,e2)
db = (tx-xd)/cad
cb = dcos(b)
eta2=ed2*cb*cb
rn = a/(1.d0-f)/dsqrt(1.d0+eta2)
dl = (ty-yd)/rn/cb
b = b+db
l = l+dl
end do
b = b/rd
l = l/rd+l0
end subroutine utm2wgs_nazo
!****************************************************
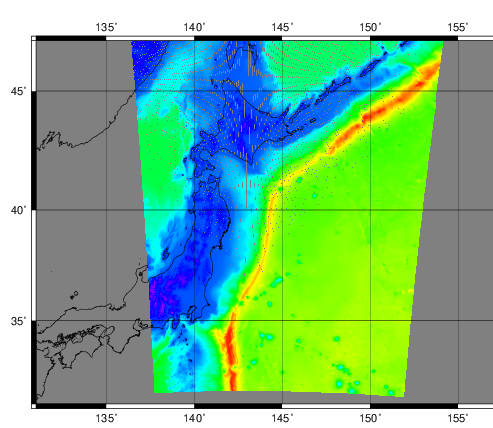
作ったプログラムがどれくらい正確か、海岸線を描いて見たいと思います。
# !/bin/bash
region=131/161/31/47
gmt makecpt -T-1000/4000/200 -Crainbow > color1.cpt
gmt xyz2grd depth_1350-01_idkd.dat -Gdepth_1350-01_idkd.grd -V -R${region} -I0.015
gmt grdimage depth_1350-01_idkd.grd -R${region} -JM20 -P -Bag -K -V > cccc.ps
gmt pscoast -R${region} -JM20 -Df -W1/0/0/0 -O -V >> cccc.ps
だいたいいい感じで他データから持ってきた海岸線データと一致してるのでたぶんOK
というわけで、僕が太古の昔に作ったプログラムの l0=143.d0 にしたらいいみたいです。もしくは、他のプログラムでUTMのZONEを指定できるなら、53.33333333でもいけるっぽいです。
(普通は整数以外を入れると計算できないけれども)
直交座標とメルカトルってやっぱこんなに違うのね。(この画像に至るまで自分が書いたプログラムのバグを含めて半日かかったorz)
変換プログラムによると、このデータの左上は( 136.30697 47.86043)なのだそうです。
まとめ
なんでこんなマニアックなことを書いたかと言うと、津波のシミュレーションのために、いろんな方が提案している断層モデルを入力する必要があるんですが、それらのモデルは緯度経度(旧測地だったりWGSだったり)するので、謎の緯度経度系を理解してないと変換できないんです!
だいたい、ドキュメントに左上の緯度経度が示されてないってどーゆーこと?
前にも書きましたが、南海トラフのデータはUTM53なので、ライブラリ等を利用することが可能です。