はじめに
「関数アート」と呼ばれるアートをご存知でしょうか。

こんなふうに猫を数式で表現してみたり$^{[1]}$、時には
こんなふうに音楽のPVそのものを数式で表してしまったりする、数学好きならではの職人芸です。
ところでこの関数アート、自動生成してしまえそうではないでしょうか。
ブラウザ上で動作する「関数アートジェネレーター」を制作したので、このツールが自動的に関数アートを生成している仕組みについて解説します。 技育展2022に出展しました。開発期間は正味1週間ほどです。
作ったもの

お手持ちの画像から、関数アートを自動的に生成することができます。
検出精度は現状まずまずの水準$^{[2]}$で、単純なイラストならいい感じに関数アートを生成してくれます。




写真でもそこそこの検出精度です。
ブラウザ上で動作するため、インストールやダウンロード不要で誰でもすぐに利用することができます。
なお、現時点で生成される関数の種類は「線分」「円弧」「多項式」の3種類です。
画像認識のライブラリや、機械学習のライブラリなどは用いず、ゼロからフルスクラッチで開発しています。
フーリエ変換などを用いれば非自明な形の関数アートが生成できそうですが、できる限り人間が理解しやすい関数アートを生成するため、今回はフーリエ変換を用いない仕様となっています。
現時点では、座標平面はx,yがそれぞれ-1〜1の範囲で固定です。
また、生成された関数アートの式を修正することはできません。
これらの機能は、そのうち追加実装するかもしれません。
概観
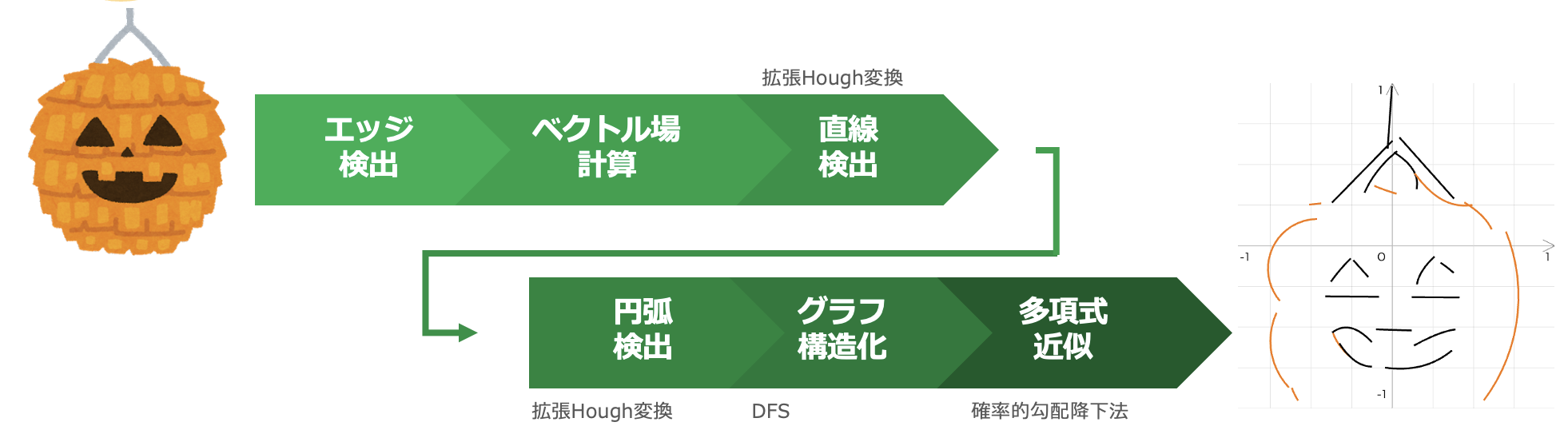
今回製作した関数アートジェネレーターは、以下の6つのステップで関数アートを生成します。
1. エッジの検出 画像のエッジを検出します。
2. 勾配の計算 画像中の各点について、局所的な傾きを算出します。
3. 線分の検出 画像に含まれる線分を検出します。
4. 円弧の検出 画像に含まれる円弧を検出します。
5. グラフ構造化 ここまでで近似できなかった点を、グラフ構造化します。
6. 多項式で近似 グラフ構造化した各連結成分を、多項式で近似します。
ここから、各ステップの動作について解説します。
なお、実装にはJavaScriptと、Canvas要素を用いています。
ステップ1 エッジ検出


ステップ1では、エッジを検出して画像を関数表現しやすくします。
突貫工事の開発だったこともあり、このステップはかなりプリミティブなエッジ検出を実装しています。
1. 画像を1ピクセルずつ走査する
2. 右隣のピクセルが存在するとき、そのピクセルとの「差」が閾値以上であれば、該当する点を中心に一定の半径の円を描く
3. 終端に到達したら終了
ここで、$2$ピクセル$\mathrm{P_1}(r_1,g_1,b_1),\ \mathrm{P_2}(r_2,g_2,b_2)$間の差とは、
$$d=\sqrt{(r_1-r_2)^2+(g_1-g_2)^2+(b_1-b_2)^2}$$
で定義しています。実際のプログラムでは、平方根の計算は省略しています。
この部分を、輝度を与える式を用いて
$$d=|0.3(r_1-r_2)+0.6(g_1-g_2)+0.1(b_1-b_2)|$$
などと改良すれば、より望ましい結果が得られるかもしれません。また、垂直方向の差分も考慮したり、キャニー法を用いるように改良したりすれば、よりよい結果が得られます。
とはいえ、関数アートジェネレーターの上では十分望ましい結果が得られているため、今回はこれでよしとします。
ステップ2 勾配の計算
エッジを検出できたら、次は検出されたエッジ上のピクセルそれぞれについて、付近の局所的な傾きを算出します。傾きを算出することで、次の処理である「線分の検出」と「円弧の検出」の正確性を高めることができます。
なおこの処理はやや負荷が高いため、適当にエッジ上のピクセルを間引いて処理を行なっています。
以下の図において、局所的な傾きを計算したい点が赤い点、サンプリングする点が青枠の点と青い点、灰色の部分が検出されたエッジを表します。また、赤い点を$\mathrm{P}$、サンプリングする直線の角度を$\alpha$、サンプリングする各点を図に示した要領で$\mathrm{P_{-n},P_{-(n-1)},\cdots,P_{n-1},P_n}$とします。
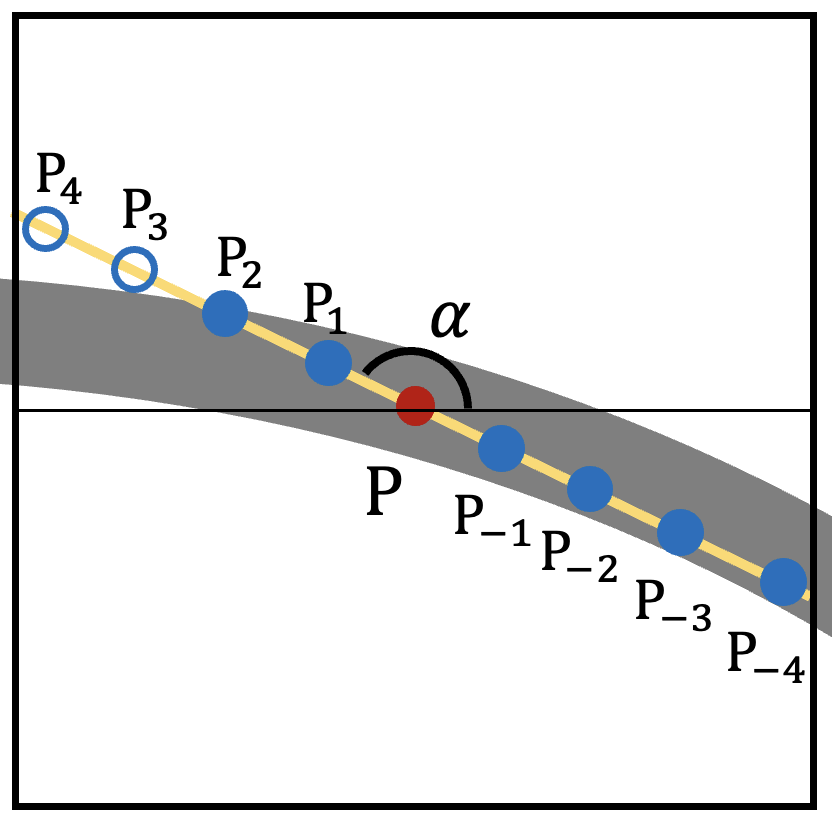
このとき、局所的な傾きは以下のステップで算出します。
1. エッジ上の各点を順番に走査する
2. $\alpha:0\leq\alpha<\pi$を一つとる。
3. $\mathrm{P}$を通る傾き$\tan\alpha$の直線上の点を一定間隔でサンプリングする。
4. サンプリングした各点のうち、エッジ上にあった点の割合$r_\alpha$を求める。
5. $r$の最大値を与える$\alpha$を$\alpha_{max}$とする。
6. $r_{\alpha_{max}}$と$r$の平均$\overline{r}$の差$d_{\mathrm{P}}$を求め、これが閾値以上だったら$\alpha_{max}$を点$\mathrm{P}$の傾きとして採用する。
この処理を行った結果得られた局所的な傾きを図示したのが以下の図です。
※処理を分かりやすくするため、検出された勾配の一部のみを描画しています。

ここからさらに、二次元配列を用意して、得られた各点の傾きを二次元配列上のデータに移し替えます$^{[3]}$。
この二次元配列を可視化したものが、本項目の冒頭で示した右側の図であり、これがステップ2のゴールです。
処理時間が気になりますが、例で示しているキノコの画像の場合、主要なデータは以下の通りです。
- ピクセル数: $540\times540$
- 傾きを調査したピクセルの個数: $1165$ (縦横4ピクセル間隔で調査)
- サンプリングの角度に対する分割数: $90$(2度ずつ直線をずらす)
- サンプリングの半径に対する分割数: $30$(片方の方向あたり)
- $s_\mathrm{P}$の閾値: $0.25$
- 閾値を超えた傾きの検知数: $1070$
これより、計算した回数の概算は以下の通りです。
- 各点あたりの傾きの計算:$90\times(30\times2)\simeq5400$
- 全ての点の傾きの計算:$5400\times1165\simeq6.3\times10^6$
極端な話、仮に全ての点がエッジだったとしても縦横$4$ピクセルずつ間引いて傾きを算出していけば、概算計算量は$10^8$を超えないので、任意の画像について現実的な時間で処理できます。
ステップ3 線分の検出


まずは直線を検出し、あとからその直線の上にある線分を抽出するという流れです。
はじめに、拡張されたHough変換を用いて直線を検出します。
拡張されたHough変換の解説については、別途記事を書きました。
Hough変換について知りたい方は、以下の記事をご覧ください。
その後、直線の補正を行います。直線の補正は以下のステップで行います。
$N_l$本の直線が検出されたとき、検出された直線を$l_n\ (0\leq n< N_l)$とし、その式が$$l_n:\ (\sin\alpha)x-(\cos\alpha)y+\beta=0$$で与えられるとします。
1. 検出された直線$l_k$を一つ選ぶ
2. $\alpha+i\delta_\alpha,\ \beta_k+j\delta_\beta$をパラメータに持つ直線$l_{ij}$について、$l_{ij}$上にあるエッジ部分の割合$r_{ij}$を調査する。なお、$i,\ j$は適当な範囲内の整数であり、$\delta_\alpha,\ \delta_\beta$は正の適当な実数である。
3. $r_{ij}$が最も大きかった$i,\ j$の組を$i_{max},\ j_{max}$とし、$l_k$のパラメータをそれぞれ$\alpha_{i_{max}},\ \beta_{j_{max}}$で置き換える。
4. $\delta_\alpha,\ \delta_\beta$を既に調査した範囲と被りが出ないよう定数倍して、同様の処理を繰り返す。
ここまでが、直線検出のステップです。
その後、検出された各直線$l_k$上の点をサンプリングし、エッジ上にあるかどうかを調査します。
$2$つ以上連続してエッジ上にある点の組を検出し、該当する範囲を「線分あり」と判定します。
ステップ4 円弧の検出


線分の時と同様に、まずは円を検出し、あとからその円の上にある円弧を抽出します。
こちらも、拡張されたHough変換を用いてまずは円の中心を抽出します。
ステップ2の段階で各点の局所的な特徴を一次式で取り出しているため、ここでは円の半径の情報はわからないことに注意が必要です。
その後、円の半径を決定します。
円の半径は、次のような流れで決定します。
$N_C$個の円の中心が検出されたとき、その中心を$\mathrm{P_n}\ (0\leq n<N_C)$と表します。
以下の図において、灰色は画像のエッジ、赤い点は$\mathrm{P}_n$を表します。

- 検出された円の中心$\mathrm{P}_k$を一つ選ぶ。
- $r=i\delta$を一定間隔で一つとる。ここで$i$は$0<i\leq i_R$を満たす自然数であり、$i_R$は適当な自然数、$\delta$は適当な正の実数である。
- $\mathrm{P}_k$を中心とする半径$r$の円上から、一定間隔で点をサンプリングする。
- サンプリングした各点のうち、エッジ上にあった点の割合$s_i$を求める。
- $t_1=s_2-s_1,\ t_2=s_3-s_2,\ \cdots, t_{i_R-1}=s_{i_R}-s_{i_R-1}$を求める。
- $t_1,\ t_2,\ \cdots t_{i_R-1}$のうち、$t_{n-1}t_{n}<0$となる$n$を見つける(※)。
- 半径$n\delta$の円を検出する。
※ $t_1,\ t_2,\ \cdots t_{i_R-1}$と順にみていったとき、正負が逆転する点を探しています。
$t$が連続関数の場合の微分に相当すると考えると分かりやすいです。
ここまでが、円検出のステップです。
その後、線分検出の場合と同様、検出された各円上の点をサンプリングし、エッジ上にあるかどうかを調査します。
$2$つ以上連続してエッジ上にある点の組を検出して「円弧あり」と判定します。
この際、$x$軸と交差するような円弧を別物と認識してしまわないように注意が必要です。
今回の実装では、エッジ上にない円弧上の点をまず見つけ、そこから一周して調査しています。
ステップ5 グラフ構造化
このステップでは、多項式で近似するための準備を行います。
まず、ステップ3とステップ4で検出された部分に相当するベクトル場の大きさを強制的に$0$とします。
その後、ベクトル場の値が0となっていない点をエッジ通りに結ぶグラフを以下の要領で作成します。

1. ステップ2で傾きが検出されていた点で、なおかつまだその付近のベクトル場の大きさが$0$ではないものを一つ選ぶ。
2. その場の傾き方向の周辺で、半径$r_0+i\delta$の円周上の点に、エッジ上の点がないかどうかを調べる。ここで、$r_0,\ \delta$は適当な正の実数、$i$は$0$から適当な整数の閾値未満の整数である。
3. エッジ上の点が見つかったらそこを新たな頂点とし、$2$点間に連結を生成したあとで同様の探索を行う。
4. エッジ上の点が見つからなかったら、$i$をインクリメントして同様の探索を行う。
5. $i$が閾値を超えたら探索を終了し、その頂点はグラフの端点とする。
上部の図のピンク色の円弧が2.で探索をおこなったラインです。ピンク色の円弧の間隔が狭いところはグラフの連結成分が生成されています。
この探索を行うと、線分や円弧で取りきれなかったエッジ上の点を滑らか$^{[4]}$に結ぶ連続成分をいくつかもったグラフ構造が得られます。
ステップ5の冒頭に示した右図をよく見ると、線分と円弧で取り去れなかったベクトル場の付近に、連結成分ごとに色分けされたグラフがあるのがわかるかと思います。
ステップ6 多項式で近似
最後のステップで、連続成分をそれぞれ多項式で近似します。
$x$と$y$の間の式を得る手順は、以下の通りです。
1. 連結成分を一つ選ぶ。
2. 確率的勾配降下法を用いて、連結成分に含まれる各点の$y$座標に対して、各点の$x$座標の累乗による重回帰を行う。
3. 2.と同様に、各点の$x$座標に対して、各点の$y$座標の累乗による重回帰を行う。
4. 2.と3.で得られた近似式のうち、残差の二乗和がより小さい方をその連結成分の近似式として採用する。
1.と2.においては、今回は正則化は行わずに残差の二乗和の最小化を行なっています。重回帰の次数は、「事前に設定した閾値」と、「連結成分に含まれる点の個数」のうち小さい方です。
なお、次数として後者が採用される場合はわざわざ確率的勾配降下法を用いずとも、LU分解を用いて連立一次方程式を解けばよいです。
しかし、極端なパラメータを持つ式が生成されることは関数アート的には望ましくないので、今回は確率的勾配降下法に統一しています。
1.と2.で得られた回帰式における残差の二乗和がいずれも閾値を上回る場合は、連結成分を強制的に中央付近で分割して再び重回帰を行います。
どちらも望ましくない場合に$x$と$y$それぞれを連結成分内の通し番号$t$で重回帰するようにすれば、パラメータ表示による近似曲線が得られそうです。
おわりに
関数アートを生成するにあたり、最終的に採用しなかったいくつかのアプローチも考えていましたが、なかなかうまくいかないものも多かったです。
また今回は時間の制約上、実装を諦めたアイディアもかなりあります。
技育展2022でのフィードバックも活かしつつ、さらにパワーアップしたものをいつかリリースしたい所存です。
最後までお読みくださってありがとうございました。
注釈
[1] 表示されている数式は猫のかかと部分(緑色の部分)の数式です。
[2] かなり曖昧ですが、見た目が不自然ではない、ということです。
[3] 傾きが検出された点それぞれについて、その近くに相当する部分の$2$次元配列の要素にその傾きを影響させる処理を実装しました。
[4] 数学的な意味ではなく、日常生活での意味における「滑らか」です。




