はじめに
画像から直線や円を検出する手法として最もポピュラーなものの一つにHough変換があります。「ハフ変換」と読むそうです。
Hough変換は最もシンプルで理解しやすい図形検出の手法であり、現在に至るまでさまざまな改良が施されています。
初学者向けに、Hough変換の流れと、局所的な傾きを用いたHough変換の拡張について解説します。
Hough変換の流れ
概要
簡単のため、ここからはまずHough変換によって直線を検出する手法について解説します。
画像は以下のようにエッジ化されているものとします。


例えば上記の右側ような画像から直線を検出することがゴールです。
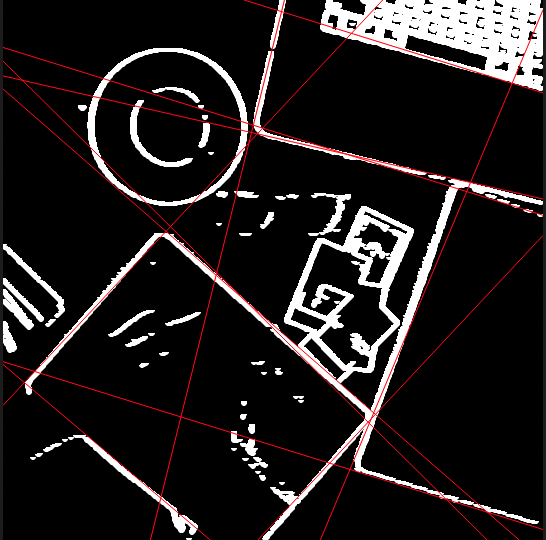
上の画像では、ノートの端とパソコンの端、タブレットの端がそれぞれ正常に検出されていることが確認できます。
下準備する
まずは、直線を扱いやすくするために画像を座標平面上に載せます。
$x,\ y$の範囲は、ここではどちらも$-1$から$1$までとしています。

投票をとる
次に、画像のピクセルを一つ一つ見ていきます。
エッジ上にないピクセルはスルーします。
あるピクセル$\mathrm{P}_0$がエッジ上にあるのを検出したとしましょう。
以下の図の第一象限にある黄色い点が$\mathrm{P}_0$です。

ピクセル$\mathrm{P}_0$に相当する座標を$(x_0,\ y_0)$とします。
ここで、検出する直線の式を
$$x\cos\theta+y\sin\theta=r\tag{1}$$
とおきます。$y$軸に平行な直線も統一的に処理するための表し方です。$\tan\theta\neq0$のもとでこれを$y$について解くと
$$y=\frac{1}{\tan\theta}x+\frac{r}{\sin\theta}$$
となるので、$\tan\theta=0$も含めれば$(1)$で任意の直線の式を網羅できていることがわかるかと思います。
さて、今エッジ上の点$\mathrm{P}_0$を見つけ、そこに相当する座標が$(x_0,\ y_0)$で与えられたのでした。
このエッジ上の点を通る直線$l$の存在を仮定すると、$l$が$\mathrm{P}_0$を通ることから、$l$の式は
$$l:\ x_0\cos\theta+y_0\sin\theta=r\tag{2}$$
と表すことができます。これは、$\theta$と$r$に関する関係式と見ることができます。
ここで、以下のような「投票箱」を用意します。
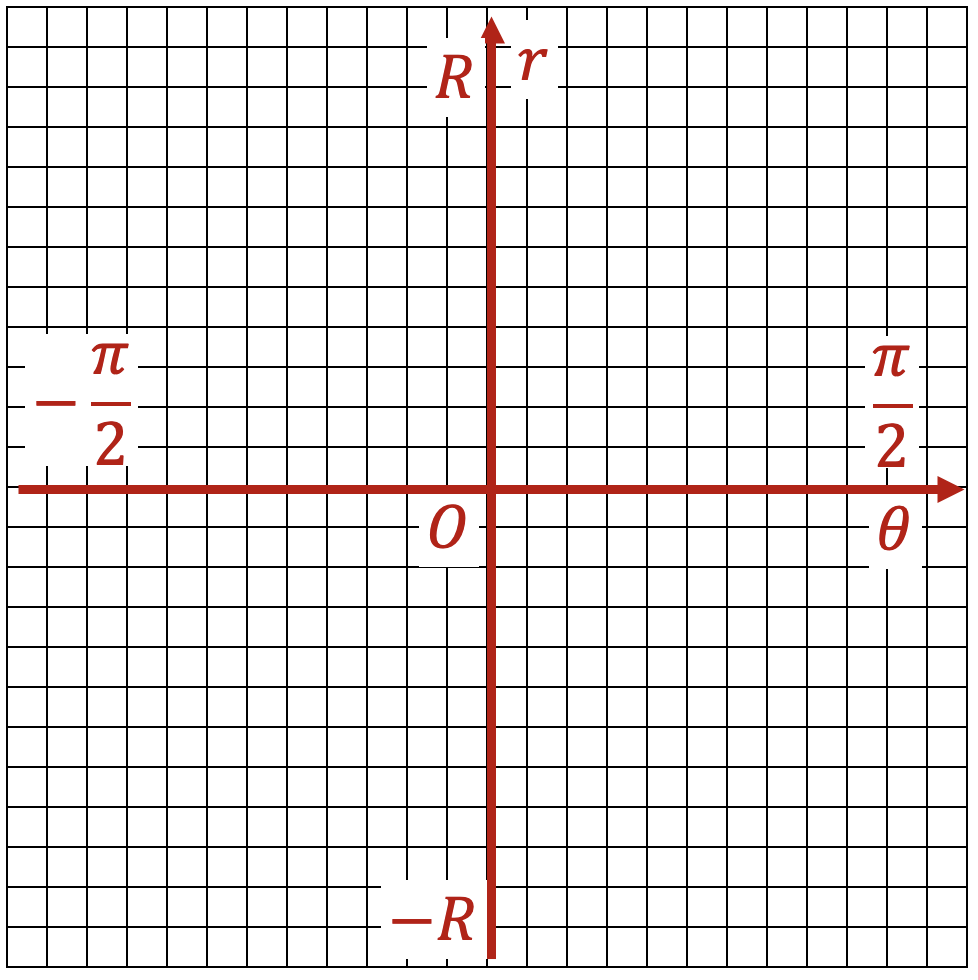
$R$は、設定した座標平面にあわせて適当に設定する正の実数です。検出された直線が座標平面内に収まるという条件から、三角不等式を用いて定めることができます。今回の場合の値は$2\sqrt{2}$です。
そして、関係式(2)の条件を満たす位置に存在する「投票箱」に票を入れていきます$^{[1]}$。
なおこのとき、三角関数の合成を用いれば(2)式は$\theta r$平面上で正弦波を表すことがわかります。

$\mathrm{P}_0$に相当する座標$(x_0,\ y_0)$を通る直線は、下図の黄色い直線のように、無数に存在します。ここでの投票は、これら無数の直線のパラメータについて投票したことに相当します。
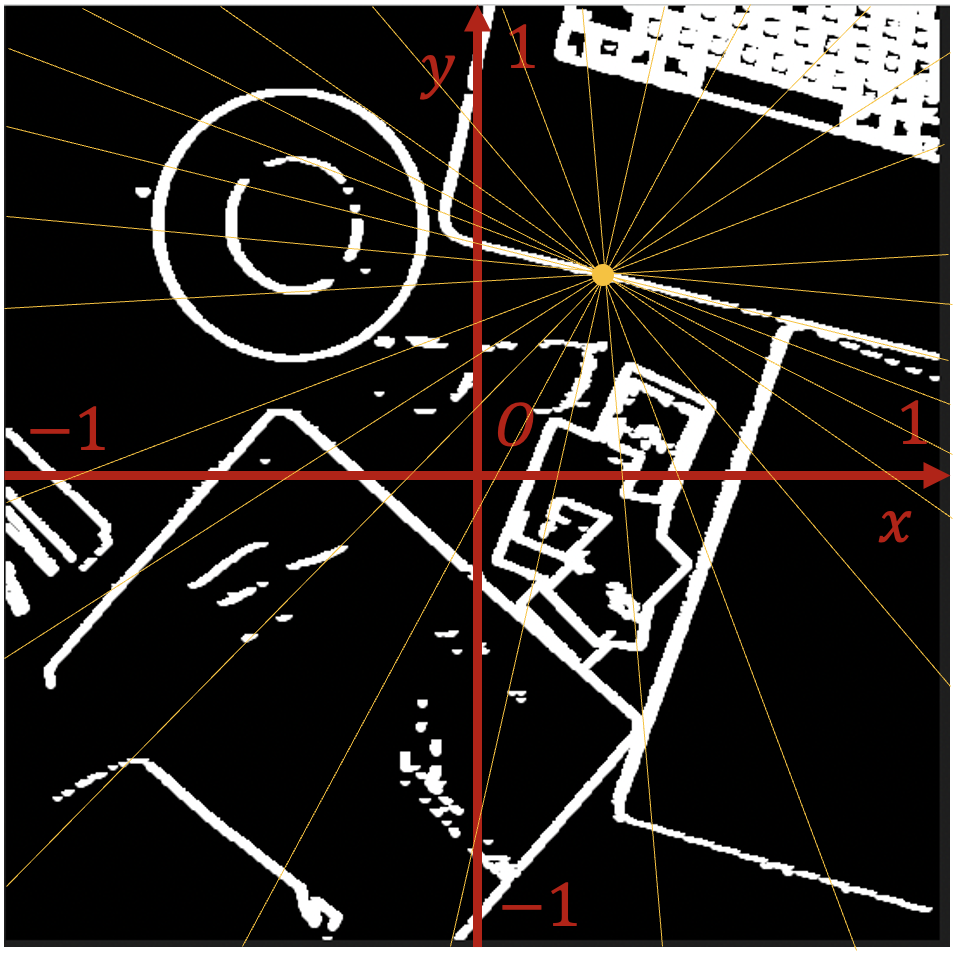
そして、ここまで紹介した処理を、エッジ上の各点について繰り返していきます。


そうすると、真のパラメータ付近の点に票が集まります(右上図)$^{[2]}$。
真のパラメータ付近からずれた点にも票が集まりますが、それは周囲の方向に分散します。
そのため、票が集まっている点に着目すれば、直線の真のパラメータ$\theta,\ r$が正しく求められるというわけです。
円検出への応用
直線検出の場合と同様に、Hough変換を用いて円を検出することもできます。
直線の場合と同様に、エッジ上の点$\mathrm{P}_0$が検出され、それに相当する座標が$(x_0,\ y_0)$であるとしましょう。
検出する円の式を
$$(x-a)^2+(y-b)^2=c^2$$
とすれば、このエッジ上の点を通る円$C$の式は
$$C:\ (x_0-a)^2+(y_0-b)^2=c^2$$
すなわち
$$C:\ (a-x_0)^2+(b-y_0)^2-c^2=0\tag{3}$$
となります。今度は$3$次元配列を用意して、(3)式を満たす点$(a,\ b,\ c)$について直線の場合と同様に投票を取っていけば、真のパラメータ付近に票が集中し、円を検出することができます。
なお、この場合パラメータ空間$(a,b,c)$内で(3)式は円錐面を表します。
$3$次元に限った話ではありませんが、このパラメータ空間のことを「Hough空間」と呼ぶそうです。
問題点
Hough変換は汎用性の高い手法ですが、いくつかの問題点も存在します。
計算量が多い
Hough変換は通常重い処理です。ピクセルごとに全て投票を取っていると計算量が膨大になってしまうため、通常は投票をとるピクセルを一定間隔で間引くなど何らかの方法で工夫を施します。最近では、投票をとるピクセルを確率的に選ぶという手法も盛んに研究されています。
隣接する直線の検出におけるジレンマ
画像によっては、画像のノイズや隣接して存在する直線などによって、複数の投票の山が生成されることがあります。近くの山同士を強制的に併合するようにすれば「同じ直線の上に、パラメータがわずかに異なる複数の直線が生成される」という状況を防ぐことができます。しかし同時に「実際には異なる直線上にあるのに、同じ直線として検出されてしまう」という問題が発生します。なお、投票後の直線の併合には、クラスタリングの手法を活かすことができます。
次元数が増えると精度が急激に低下する
Hough変換の致命的な欠点として、パラメータ数が多い場合には急激に精度が低下するという点があります。実際の画像にはノイズも多く含まれるため、パラメータ付近の広い範囲に点が分散するようになり、実用上使い物にならなくなってしまうのです。そのための解決策として、次章で紹介する局所的な傾きを用いる方法があります。
局所的な傾きを用いたHough変換の拡張
ここからは、主に円を検出するためにHough変換を拡張した手法の解説です。
独自に考えた手法をベースに解説しますが、古くから類似の手法が提案されているようです$^{[3]}$。
直線の場合はそれほど恩恵がありませんが、わかりやすさのためまずは直線の場合について解説します。
下準備する
従来のHough変換の際と同様に、まずは画像に座標平面を設定します。
その次に、エッジ上の各ピクセルに対し、その付近の局所的な傾きを求めます。
局所的な傾きはエッジ検出の過程で副次的に求められることも多いですし、愚直な実装でも現実的な時間で求まります。
今回の画像の場合、局所的な傾きを図示すると以下のようになります$^{[4]}$。

投票をとる
エッジ上の点$\mathrm{P}_0$が検出され、相当する座標が$(x_0,\ y_0)$であったとします。また、その場所の局所的な傾きを表す角度が$\theta_0$であったとします(下図)。

(ただし、$\theta_0$は$-\pi/2<\theta_0\leq\pi/2$の範囲で、$x$軸から反時計回りの向きに取ります。すなわち上図の場合$\theta_0<0$です)
ここで、投票箱を用意します。
$\mathrm{P}_0$を通る直線$l$の存在を仮定すると、$l$の式は
$$l:\ x_0\cos\theta+y_0\sin\theta=r\tag{4}$$
と表すことができます。これは$\theta$と$r$に関する関係式と見ることができますが、$\theta_0$が既知であることに注意すると、これは$(\theta,\ r)$平面上におけるある一点$(\theta_0,\ x_0\cos\theta_0+y_0\sin\theta_0)$を表すことがわかります。
したがって、$P_0$に関する投票を実施したあとの投票箱は以下のようになります。

この投票をエッジ上の全ての点について実施すると、投票実施後の投票箱は以下のようになります。

先に局所的な情報を調べておくことで、無駄な投票を削減し、精度を向上させることができます。
円検出への応用
同様に、円検出へ応用することも可能です。
エッジ上の点$\mathrm{P}_0$が検出され、相当する座標が$(x_0,\ y_0)$、局所的な傾きを表す角度が$\theta_0$であったとします。
このとき、$\mathrm{P}_0$を通り、$x$軸となす角度が$\theta$で表される直線の方程式は
$$(\sin\theta_0)x-(\cos\theta_0)y+y_0\cos\theta_0-x_0\sin\theta_0=0\tag{5}$$
と表されます。
一方、円の方程式を
$$C:\ (x-a)^2+(y-b)^2=c^2$$
と表すと、$C$上の点$(x_0,\ y_0)$における接線の方程式は
$$(x-a)(x_0-a)+(y-b)(y_0-b)=c^2$$
すなわち
$$(x_0-a)x+(y_0-b)y+a^2+b^2-c^2-ax_0-by_0=0\tag{6}$$
と表されます。(5)と(6)の係数を比較して
\begin{cases}
\sin\theta_0(y_0-b)&=-\cos\theta_0(x_0-a)\\
(a^2+b^2-c^2-ax_0-by_0)\sin\theta_0&=(x_0-a)(y_0\cos\theta_0-x_0\sin\theta_0)
\end{cases}
を満たす$3$次元空間内の点$(a,\ b,\ c)$に投票すればよいです。ゴツそうな見た目をしていますが、第二式の右辺にある$(y_0\cos\theta_0-x_0\sin\theta_0)$などは単なる数値なので、実際はそれほどややこしくありません。
なお、$3$次元空間内に投票するのはコストがかかるため、次で紹介するような改良も可能です。
円検出における改良
円の半径と中心の座標を同時に発見するのは大変なので、困難を分割します。すなわち、先に円の中心を求め、後からその円の半径を求めるという戦略をとります。
円の中心の座標を求めます。
エッジ上の点$\mathrm{P}_0$における局所的な傾きと直交する傾きを持ち、点$\mathrm{P}_0$を通る直線$m$の式は
$$m:\ (\cos\theta_0)x+(\sin\theta_0)y-x_0\cos\theta_0-y_0\sin\theta_0=0$$
と表されます。
ここで、円の中心を求めるための$2$次元の投票箱を用意し、$m$上にある投票箱に投票していきます。
円上の点から、その点における傾きと直交する向きに引かれた直線は必ず円の中心を通るので、円上の点からの投票を重ねると投票箱は以下のようになります。

ここで投票が重なった点が、円の中心です。
その後、検出された中心とエッジ間の距離を計算します。ここでは$1$次元の投票が実施され、多く投票が集まっているところがその円の半径となります。もちろん、同じ点を中心に持ち半径が異なる複数の円が検出される可能性もあります。
おわりに
画像検出っておもしろいですね。パラメータが多い場合は、上手くHough空間を定めることでHough変換したあとのパラメータをさらにHough変換する、なんてこともできるんでしょうか。Hough変換は応用や改良の余地が大きく、工夫しがいがありました。
脚注
[1] ここでは説明のために投票箱を大雑把に区切っています。
[2] 実際はここまで綺麗になりません。また、図においては、黄色い点たちが乗る直線上以外の点からの投票は省略しています。
[3] D.H. Ballard, "Generalizing the Hough Transform to
Detect Arbitrary Shapes", PR, 13-2, 111/122 (1981)
[4] 図ではエッジの周りにも細かい流れがありますが、本来これは除去した方が良い結果が得られます。
