はじめに
強化学習について学んだので、備忘録も兼ねて内容をまとめます。
第1回である本稿では、強化学習とはなにかを紹介します。その後、マルコフ決定過程を始めとした種々のマルコフ過程について概観します。なお、強化学習にはSutton & Bartoによるバイブル的な参考書"Reinforcement Learning: An Introduction"があり、この記事もここに書かれている内容を元に作成しています。すべて英語ですが、参考にしてください。
次回 ▶ 第2回「【強化学習】第2回 - ベルマン方程式と方策反復法(PI)、価値反復法(VI)について解説」
強化学習とは?

強化学習とは、ある環境内におけるエージェントが取るべき行動を決定することを目的とする、機械学習の一種です。2015年にプロ棋士に勝利したことで大きな話題を呼んだAlphaGoでも、機械学習の技術が応用されています。SNSや通販サイトにおけるリコメンド機能や、自動運転なども強化学習が活用されている一例です。
「エージェント」「環境」といった、強化学習におけるキーワードについてくわしく見ていきましょう。例として、ここでは以下のような火星探索ロボットを考えてみます。

まずエージェントとは、この火星探索ロボットのことです。環境はこの場合、火星を指します。
機械学習においてエージェントは、「状態」を保持しています。また、「行動」を実施することによって「報酬」を得ることができます。
例えばこの火星探索ロボットが①〜⑤の範囲を移動することができ、現在は真ん中である③の地点にいるとしましょう。このとき、火星探索ロボットの状態は③です。

火星探索ロボットは、①〜⑤をはみ出ない範囲で「左に移動」か「右に移動」のどちらかを選択できるものとします。「左に移動」「右に移動」がそれぞれ行動です。
さらに、状態①のときに報酬1を、状態⑤のときに報酬5をそれぞれ獲得できるとします。①と⑤以外の状態の時には報酬を獲得できません。このとき、火星探索ロボットはどのようなルールに沿って行動すれば報酬を最大化できるでしょうか。
この問題を考えるのが強化学習です。なお、エージェントが従う行動のルールのことを「方策」といいます。言い換えると、「報酬をできる限り大きくするような方策を見つける」ことが強化学習のゴールです。
種々のマルコフ過程
ここからは少々理論的な話に入っていきます。数式が多く登場しますので、ゆっくり読んでください。
まずは強化学習を取り扱うために必要なマルコフ過程について解説します。まずはマルコフ過程について扱います。その後、強化学習で頻繁に登場するマルコフ決定過程やマルコフ報酬過程へと拡張していきましょう。
マルコフ性
時刻 $t$ における状態 $s$ を $s_t$、時刻 $t$ における行動 $a$ を $a_t$、時刻 $t$ で得た報酬を $r_t$ でそれぞれ表します。また、時刻 $t$ までの状態や行動、報酬の情報をまとめて $h_t=(a_1,\,s_1,\,r_1,\cdots,\,a_t,\,s_t,\,r_t)$で表します。
このとき状態 $s_t$ がマルコフ性を持つとは、
$$
\begin{align*}
p(s_{t+1}\,|\,s_t,\,a_t)=p(s_{t+1}\,|\,h_t,\,a_t)
\end{align*}
$$
が満たされることをいいます。初見ではなかなか意味のわかりにくい等式ですが、これは時刻 $t+1$ における状態が、時刻 $t$ における状態と行動のみに依存する、ということを表しています。別の言葉でいうと、時刻 $t-1$ 以前の状態や行動、時刻 $t$ 以前に獲得した報酬は時刻 $t+1$ の状態に影響を与えない、ということです。
マルコフ過程
$S$ を、とり得る状態を要素に持つ集合であるとします。また $P$ を、遷移を表すモデルとし、 $p(s_{t+1}=s',|,s_t=s)$ で、「時刻 $t$ における状態が$s$であるときに、時刻 $t+1$ における状態が $s'$ になる条件付き確率」を表すものとします。
このとき、タプル $M=(S,,P)$ のことをマルコフ過程といいます。すなわち、マルコフ過程とは「状態」と「 $t$ から $t+1$ への遷移確率」という2つの情報を持ったモデルのことです。
$\quad S:\,$とり得る状態を要素に持つ集合
$\quad P:\,p\,(s_{t+1}=s'\,|\,s_{t}=s)$ を与える遷移モデル
$S$ が有限のとき、状態間の遷移を表す $P$ は行列として表現することができます。例えば先程取り上げた火星探査ロボットが、向かって右側に60%の確率で、向かって左側に40%の確率で移動するとしましょう。ただし、状態①や⑤で端にきていて片方にしか移動できない場合は、必ず移動できる方向へ移動するものとします。なお、ここでは一旦報酬と行動は忘れてください。

このとき、この火星探査ロボットの遷移を表す行列$P$は以下のようになります。
$$
P=
\begin{pmatrix}
0 & 1 & 0 & 0 & 0 \\
0.4 & 0 & 0.6 & 0 & 0\\
0 & 0.4 & 0 & 0.6 & 0 \\
0 & 0 & 0.4 & 0 & 0.6\\
0 & 0 & 0 & 1 & 0 \\
\end{pmatrix}
$$
例えば状態③から状態②に遷移する確率は40%です。これは $P_{32}=0.4$ であることに対応しています。また、状態③から状態④に遷移する確率は60%です。これは $P_{34}=0.6$ であることに対応しています。
このような確率の遷移を表した行列 $P$ のことを、確率行列、あるいは遷移行列と呼びます。ある状態から次の状態へ遷移する確率の和は $1$ になるので、確率行列の各行の和は必ず $1$ となります。
マルコフ過程は、Googleの検索システムや自然言語処理などで活用されている概念です。ここからはマルコフ過程を強化学習へ活用するため、今紹介したマルコフ過程を拡張していきます。
マルコフ報酬過程(MRP)
マルコフ報酬過程とは、マルコフ過程の概念を拡張したものです。以下の $4$ つの要素 $S,\,P,\,R,\,\gamma$ からなるタプル $M=(S,\,P,\,R,\,\gamma)$ として表現されます。なお、以下の $R$ に登場する $r_t$ は時刻 $t$ における報酬です。
$\quad S:\,$とり得る状態を要素に持つ集合
$\quad P:\, p\,(s_{t+1}=s'\,|\,s_{t}=s)$ を与える遷移モデル
$\quad R:\, R\,(s_t=s)=\mathbb{E}[r_t\,|\,s_t=s]$ で表現される報酬関数
$\quad \gamma:\, \gamma\in[0,\,1]$を満たす割引率
$S$ と $P$ はマルコフ過程のときと全く同じです。異なるのは報酬関数と割引率ですね。
報酬関数は、時刻 $t$ における状態が $s$ であるときの報酬 $r_t$ の期待値を与える関数です。割引率は $0$ から $1$ の範囲で、モデルに応じて適当に設定します。
火星探査ロボットで、再び状態①の報酬を $1$、状態⑤の報酬を $5$、その他の状態の報酬を $0$ と定めてみましょう。割引率 $\gamma$ は $0.5$ と定めます。これで火星探査ロボットを表すマルコフ報酬過程となりました。

状態価値関数
マルコフ報酬過程において、将来的に得られる報酬の見込みを考えてみます。
マルコフ過程に従う一連の状態遷移の列のことを、エピソードといいます。例えば火星探索ロボットが状態③から始まり、③→④→③→④→⑤と遷移していった場合、「③→④→③→④→⑤」がエピソードです。また、このエピソードに含まれる状態遷移の数をHorizonといいます。エピソード「③→④→③→④→⑤」におけるHorizonは $5$ です。
時刻 $t$ におけるReturn $G_t$ を以下の式で定義しましょう。各エピソードについて、Horizonの範囲内まで足し算していきます。
$$
\begin{align*}
G_t=r_t+\gamma r_{t+1}+\gamma^2 r_{t+2}+\gamma^3 r_{t+3}+\cdots
\end{align*}
$$
これを用いて、状態価値関数は以下のように定義されます。
$$
\begin{align*}
V(s)=\mathbb{E}[\,G_t\,|\,s_t=s\,]
\end{align*}
$$
つまり、$V(s)$ は時刻 $t$ における状態が $s$ のときの、将来的に得られる報酬の見込みを表します。大雑把に捉えれば、$V(s)$ は状態 $s$ に期待できる報酬そのものです。戦略を考える上では原則として、$V(s)$ の値が高ければ高いほど、その状態 $s$ を積極的に狙っていくべきだということになります。
例えば先程も取り上げたエピソード「③→④→③→④→⑤」のReturnである $G_1$ を考えます。各時刻における状態と報酬をまとめると次の表のようになりますね。
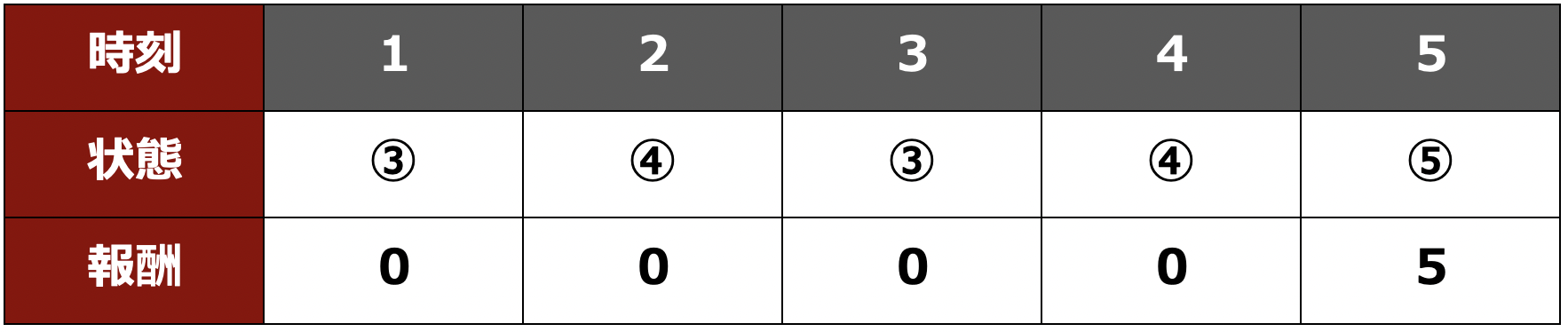
したがって、割引率 $\gamma=0.5=1\,/\,2$ のとき $G_1$ は
$$
\begin{align*}
G_1&=0\cdot1+0\cdot\frac{1}{2}+0\cdot\frac{1}{4}+0\cdot\frac{1}{8}+5\cdot\frac{1}{16}\\
&=0.3125
\end{align*}
$$
と計算することができます。
なお $\gamma$ についてはケースバイケースで適当な値を設定しますが、$G_t$ の式から容易にわかるように、以下の性質があります。
- $\gamma=0$ のとき、現在の報酬しか気にかけない
- $\gamma=1$ のとき、将来的な報酬も現在の報酬と同程度に重視する
マルコフ決定過程(MDP)
マルコフ決定過程とは、マルコフ報酬過程に行動の概念を追加したものです。
$S,\,A,\,P,\,R,\,\gamma$ からなるタプル $M=(S,\,A,\,P,\,R,\,\gamma)$ として表現されます。$S,\,P,\,R,\,\gamma$はマルコフ報酬過程の場合と全く同じです。
$\quad S:\,$とり得る状態を要素に持つ集合
$\quad A:\,$とり得る状態を要素荷物集合とり得る行動を要素に持つ集合
$\quad P:\,$ $p\,(s_{t+1}=s'\,|\,s_{t}=s,\,a_{t}=a)$ を与えるモデル
$\quad R:\,$ $R\,(s_t=s,\,a_t=a)=\mathbb{E}[r_t\,|\,s_t=s,\,a_t=a]$ で表現される報酬関数
$\quad \gamma:\,$ $\gamma\in[0,\,1]$を満たす割引率
なおマルコフ決定過程は以上の5つの要素に加え、以下の二つの要素も含むことがあります。
$\quad \rho_0:\,$ $\rho_0:S\to\mathbb{R}^+$ で表される初期状態の分布
$\quad T:\,$ $T\subset S$ である、終端となる状態の集合
マルコフ報酬過程から追加された要素は $A$ のみですが、$A$ が追加されたことによって $P$ と $R$ の式も変化します。$P$ の式が $p\,(s_{t+1}=s'\,|\,s_{t}=s)$ から $p\,(s_{t+1}=s'\,|\,s_{t}=s,\,a_{t}=a)$ に変化したのは、マルコフ決定過程の場合の状態遷移が「現在の状態」と「その時の行動」の2つによって決定されることを表しています。報酬についても同様です。なおマルコフ決定過程における報酬は、ある時刻における状態 $s$ のみによって決定されることもあれば、ある時刻における状態 $s$ とその時の行動 $a$、その後の状態 $s'$ の3要素 $(s,\,a,\,s')$ の3要素によって決定されることもあります。

例えば火星探索ロボットの場合、行動として「左に動こうとする」「右に動こうとする」の2つが考えられます。なぜ行動があるのに状態遷移が確率的なのかというと、実際の動作は必ずしも意図した通りにならないことがあるからです。

例えば上のように状態①と状態②の間に坂道があり、状態②から左に移動しようとしても30%の確率で右側の状態③にすべり落ちてしまうとします。それ以外は意図した通りに動いてくれるとしましょう。「左に動こうとする」と「右に動こうとする」という行動をそれぞれ $l,\,r$ で表すと、例えば
$$
p\,(s_{t+1}=1\,|\,s_t=2,\,a_t=l)=0.7\\
p\,(s_{t+1}=3\,|\,s_t=2,\,a_t=l)=0.3\\
p\,(s_{t+1}=3\,|\,s_t=2,\,a_t=r)=1.0\\
$$
となります。上から順番に
- 状態②で左に動こうとしたとき状態①に移動できる確率が70%
- 状態②で左に動こうとしたとき状態③に移動してしまう確率が30%
- 状態②で右に動こうとしたとき状態③に移動できる確率が100%
を表していますね。
マルコフ決定過程&方策
エージェントは現在の状態に応じて、一定の確率で次の行動を選択するとします。エージェントが行動を決定する際のルールを表すのが、方策 $\pi$ です。具体的には以下の式で表現されます。
$$
\pi\,(a\,|\,s)=P\,(a_t=a\,|\,s_t=s)
$$
時刻 $t$ における状態が $s$ のとき、行動 $a$ を実施する確率を与えるのが方策ということです。それでは、マルコフ決定過程に方策の概念を追加するとどうなるでしょうか。
実はマルコフ決定過程に方策を追加したものは、マルコフ報酬過程として取り扱うことができます。ある方策 $\pi$ に従って行動するマルコフ決定過程を考えましょう。このとき
$$
R^{\pi}(s)=\sum_{a\in A}\pi(a\,|\,s)R(s,a)\\
P^{\pi}(s'\,|\,s)=\sum_{a\in A}\pi(a\,|\,s)P(s'\,|\,s,\,a)
$$
と定めれば、$(S,\,R^{\pi},\,P^{\pi},\,\gamma)$ は方策 $\pi$ に従って行動するマルコフ決定過程と等価なマルコフ報酬過程になっています。
これだけではわかりにくいと思うので、具体的に考えてみます。マルコフ決定過程の説明の際に用いた、状態①と状態②の間に坂道がある状況を考えてみましょう。先ほどと同様に坂道を乗り越えられる確率は70%、滑り落ちてしまう確率は30%とします。さらに、火星探索ロボットが状態②にいるとき、確率60%で行動 $l$ を、確率40%で行動 $r$ を選択するという方策 $\pi$ を考えます。

図中の黄色い60%と40%はあくまでも「移動しようとする確率」であり、実際に移動できるかどうかは別であることに気をつけてください。
このとき、状態②から状態①へ移動する確率はどうなるでしょうか。60%で状態①への移動を試みた際に、それが成功する確率が70%ですから、左へ動こうとして状態①へ移動する確率は42%です。右へ動こうとした際は100%で状態③へ移動できるため、このとき状態①へ移動してしまうことはありません。

よって、方策 $\pi$ に従った際に状態②から状態①へ移動する確率は42%です。どの程度の確率で行動を選択するのかを表した方策という情報があれば、各状態間の遷移確率を具体的に求められるため、マルコフ報酬過程として扱えるということです。
おわりに
強化学習の基礎とマルコフ過程について扱いました。マルコフ過程の考え方は、これから強化学習を学んでいく上での重要な基盤となります。次回は今回導入した概念を用いて、期待できる報酬が最大化されるような方策を求めるアルゴリズムについて扱います。
訳出について
専門用語は、以下のように訳出しています。機械学習分野はしっかりとした和訳が確立されていないものも多いので、そのようなものは英語のままにしました。
| 日本語 | 英語 |
|---|---|
| 方策 | policy |
| 割引率 | discount factor |
| マルコフ決定過程 | Markov Decision Process |
| マルコフ報酬過程 | Markov Reward Process |
参考文献
- Sutton & Barto, "Reinforcement Learning: An Introduction", http://incompleteideas.net/book/the-book.html (最終閲覧: 2022/11/03)
- icoxfog417, "ゼロからDeepまで学ぶ強化学習", https://qiita.com/icoxfog417/items/242439ecd1a477ece312 (最終閲覧: 2022/11/03)
- (画像素材) Unsplash, https://unsplash.com/ (最終閲覧: 2022/11/03)
