Statsmodelsによる自己回帰モデル入門

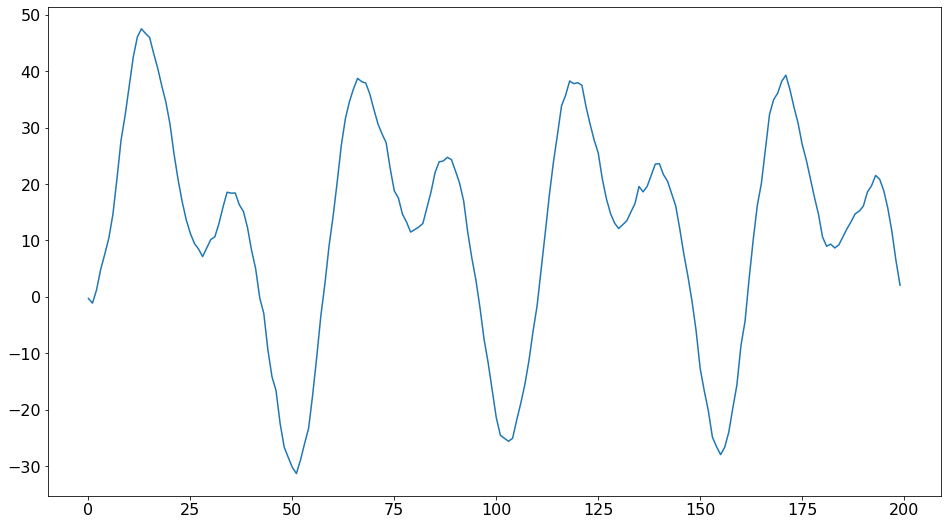
時系列データは時間の経過とともに観測されるデータのことです。期間$t=1,2,\cdots,T$で観測されるデータを$Y_1,Y_2\cdots,Y_T$、または{$Y_t$}$_{t=1}^{T}$と書きます。統計学ではこの観測値と確率変数を用いて、観測値の性質を調べていきます。観測値は確率変数の一部であるとしてモデル化できるかどうかを検討しながら、その特徴を捉えていきます。

観測値が得られるとその観測値の平均や分散を求めることができます。また、そのデータの異なる時点の共分散を求めることができ、それを自己共分散と呼びます。時点$t$におけるラグ、または時間差$h$の自己共分散を$h$次の自己共分散といいます。自己共分散を基準化したものが自己相関です。

確率変数の同時分布や基本統計量が時間の経過によって変化しないときその確率過程を定常過程といいます。多くの場合、期待値と共分散が時間の経過に対して定常であることを仮定して、弱定常性と呼びます。同時分布が時間のどの時点においても同じであれば強定常といいます。時系列データの平均が観測時点$t$に依存せず有限で、自己共分散も観測時点$t$に依存せずに時間差$h$のみに依存する場合、その系列は共分散定常時系列といいます。

共分散定常仮定のうち、平均がゼロ、$h\ne 0$のすべての自己共分散がゼロであるものをホワイトノイズといいます。

自己回帰移動平均モデルは

{\displaystyle Y_{t}=\varepsilon _{t}+\sum _{i=1}^{p}\varphi _{i}Y_{t-i}+\sum _{i=1}^{q}\theta _{i}\varepsilon _{t-i}.\,}

と表せます。$\varphi$は自己回帰係数、$\theta$は移動平均係数です。

 X_t = c + \sum_{i=1}^p \varphi_i Y_{t-i}+ \varepsilon_t .\,

は自己回帰モデルでARモデルとも呼ばれます。

１変量ARモデルの推定法としては
（１）Yule-Walker法
（２）最尤法
（３）最⼩⼆乗法（Householder法）
（４）PARCOR法
があります。それぞれの特徴はつぎのようにまとめることができます。

出所：http://www.mi.u-tokyo.ac.jp/mds-oudan/lecture_document_2019_math7/時系列解析（６）_2019.pdf　北川源四郎

StatsmodelsはPythonというプログラミング言語上で動く統計解析ソフトです。statsmodelsのサンプルを動かすにはPCにPythonがインストールされている必要があります。まだインストールされていない方はJupyter notebookのインストールを参照してください。Jupyter notebookはstatsmodelsを動かすのに大変便利です。

また、線形回帰に興味のある方はstatsmodelsによる線形回帰 入門も参考にしてみてください。

自己回帰

本記事は

https://www.statsmodels.org/stable/examples/notebooks/generated/autoregressions.html
をChatGPTを用いて翻訳し、加筆、適時修正したものです。

Autoregressive AR-X(p) model (Autoreg model)

自己回帰モデルは次のようなダイナミクスによって特徴づけられます。

$$y_t=\delta+\phi_1 y_{t-1}+\cdots+\phi_py_{t-p}+\epsilon_t$$

完全な仕様は

$$y_t=\delta_0+\delta_1t+\phi_1 y_{t-1}+\cdots+\phi_py_{t-p}+\epsilon_t+\sum_{i=1}^{s-1}\gamma_id_i+\sum_{j=1}^m \kappa_jx_{t,j}+\epsilon_t$$

ここで

• $d_i$ は，mod(t,period)=i の場合に 1 となる季節ダミーである．モデルが定数（c）を含む場合，期間 0 は除外される． mod(t, period) は、数学的な「モジュロ」演算（剰余演算）を指します。具体的には、mod(t, period) は、時点 t を周期 period で割ったときの余りを表します。たとえば、period = 4 とし、季節性が季節ごとに異なる場合を考えます。このとき、t=1, 5, 9, ... などの時点で d_1 = 1 となり、t=2, 6, 10, ... の時点で d_2 = 1 となる、というように季節ごとのダミー変数が設定されます。モデルが定数項を含む場合、周期の初め（period = 0 の場合）は通常除外されます。これは、定数項が既に平均的な影響をモデル化しているため、その周期の初めの影響を別途モデル化する必要がないためです。その結果、残りの周期（1, 2, ..., s-1）だけが季節ダミー変数として用いられます。

• $t$ は，最初の観測で 1 から始まる時間トレンド(1,2,...)である。

• $x_{t,j}$ は外生的回帰変数である．モデルを定義する際には、これらは左側の変数に時間的に配置されていることに注意。

• $\epsilon_t$ はホワイトノイズ過程であると仮定。

ーAutoRegの主な特徴と機能ー

statsmodelsのAutoReg クラスは、Pythonで自己回帰（AR）モデルを分析するための強力なツールです。

1. 自己回帰モデリング:
   AutoReg は、時系列データの自己回帰（AR）モデルをフィッティングするために使用されます。これは、時系列の現在の値が過去の一定数の値に基づいて予測されるモデルです。

2. ラグの選択:
   ユーザーは、モデルに含めるラグ（遅延）の数を指定できます。ラグの数はモデルの複雑さとフィッティング精度に影響を与えます。

3. 季節性と外生変数のサポート:
   AutoReg は、季節性成分や外生変数（AR-Xモデル）をモデルに組み込むオプションを提供します。これにより、モデルは追加の情報源からの影響を考慮できるようになります。

4. 統計的推定:
   最小二乗法（OLS）を用いてパラメータ推定を行います。モデルの適合度を評価するための統計的検定と診断も提供されます。

5. 予測:
   モデルを使用して、未来の値を予測することができます。これは、時系列データの将来的な傾向やパターンを把握するのに役立ちます。

AutoRegの引数は：

• 決定論的項(trend）

  n: 決定論的な項無し

  c: 定数(デフォルト)

  ct. 定数と時間トレンド

  t: 時間トレンドのみ

• 季節性のダミー変数(seasonal)

  Trueはs-1ダミーを含み、sは時系列の期間（例えば、月次の場合は12）である。

• オーダーメイドの決定論的な項（deterministic)

  DeterministicProcessを受け入れる

• 外生変数 (exog)

  DataFrameまたは配列の外生変数をモデルに含める

• 選択されたラグ（lags）の省略

  lagsが整数の反復可能なものであれば、これらのものだけがモデルに含まれる。

つぎの最初のセルは、標準パッケージをインポートし、インラインで表示されるように設定します。

%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import pandas_datareader as pdr
import seaborn as sns
from statsmodels.tsa.ar_model import AutoReg, ar_select_order
from statsmodels.tsa.api import acf, pacf, graphics

つぎのセルは、プロットスタイルを設定し、matplotlib用のpandasの日付変換器を登録し、デフォルトの図形サイズを設定します。

sns.set_style('darkgrid')
pd.plotting.register_matplotlib_converters()
# Default figure size
sns.mpl.rc('figure',figsize=(16, 6))

最初の例では、季節調整されていない米国の住宅着工件数の前月比成長率を使用しています。季節性は、ピークとトラフの規則的なパターンから明らかです。AutoRegを使用する際の警告を避けるために、時系列の頻度を "MS" (month-start)に設定しました。

data = pdr.get_data_fred('HOUSTNSA', '1959-01-01', '2024-01-01')
housing = data.HOUSTNSA.pct_change().dropna()
# Scale by 100 to get percentages
housing = 100 * housing.asfreq('MS')
fig, ax = plt.subplots()
ax = housing.plot(ax=ax)

まずはAR(3)から始めましょう。これはこのデータを表現する良いモデルではありませんが、APIの基本的な使い方を示すために用います。

mod = AutoReg(housing, 3, old_names=False)
res = mod.fit()
print(res.summary())

＊基本情報＊

• 依存変数（Dep. Variable）: HOUSTNSA。このモデルが予測する時系列データ。

• 観測数（No. Observations）: 778。このモデルが使用するデータポイントの数。

• モデル（Model）: AutoReg(3)。自己回帰モデルで、3つのラグ（遅れ）を使用しています。

• 方法（Method）: Conditional MLE（条件付き最尤推定法）。

• 標準偏差（S.D. of innovations）: 15.009。モデルの誤差項（イノベーション）の標準偏差。

• 日付と時間（Date, Time）: モデルが実行された日付と時間。

• AIC, BIC, HQIC: これらはモデルの適合度を測る情報基準です。一般に、これらの値が小さいほどモデルの適合度が高いとされます。

  AIC(赤池情報量基準)
  BIC(ベイズ情報量基準)
  HQIC(Hannan-Quinn情報量基準)

＊係数（Coef）とその統計＊

• const: 定数項の係数。このモデルでは 1.0998。
• HOUSTNSA.L1, L2, L3: それぞれ1期前、2期前、3期前のHOUSTNSAの係数。例えば、HOUSTNSA.L1 の係数は 0.1835 で、前期の値が現在の値に与える影響を示しています。
• std err: 係数の標準誤差。
• z: Zスコア。係数が統計的に有意かどうかを評価するためのスコア。
• P>|z|: 係数が統計的にゼロと異なる確率。通常、0.05以下であれば統計的に有意。
• [0.025 0.975]: 係数の95%信頼区間。

＊モデルの根（Roots）＊

1. 実数（Real）と虚数（Imaginary）:
   ARモデルの解析では、モデルの特性根（characteristic roots）が計算されます。これらは、モデルの安定性や振る舞いを理解するために重要です。実数と虚数の部分は、これらの特性根の構成要素です。実数部分がモデルの振幅を、虚数部分が振動の性質を反映します。

2. モデュラス（Modulus）:
   モデュラスは特性根の大きさ（絶対値）を示し、モデルの安定性を評価するために使用されます。一般に、モデルが安定であるためには、すべての特性根のモデュラスが1未満でなければなりません。

3. 周期（Frequency）:
   周期は、特性根が示す時系列データの循環的な振る舞いの長さを示します。これは、時系列データに含まれる周期的なパターンや波の長さを理解するのに役立ちます。

これらの値は、ARモデルの振る舞いを理解し、モデルがデータのどのような特性を捉えているかを分析するために重要です。特に、時系列データの動的な特性や周期性を評価する際に役立ちます。また、モデルの安定性や予測の信頼性を判断する際にも重要な指標となります。

モデルの「根」は、モデルの動的特性を示します。ここにリストされているのは複素数の根で、モデルが安定しているかどうか、どのような振る舞いを示すかを示します。これらの根が単位円の外側にある場合、モデルは安定とみなされます。

モデルの根が単位円の外側にあるかどうかを判断するには、それらの根の絶対値（modulus）を考慮します。単位円は複素平面上の円で、中心が原点（0,0）で半径が1の円です。モデルの根がこの単位円の外側にある場合、モデルは安定していると考えられます。複素数の根（例：a + bi）の絶対値は、次の式で計算されます：

$$ \text{Modulus} = \sqrt{a^2 + b^2} $$

この絶対値が1より大きい場合、その根は単位円の外側にあります。自己回帰モデルにおいて、全ての根の絶対値が1より大きい場合、そのモデルは安定しているとみなされます。これは、時間が経過するにつれて、モデルの影響が減衰し、時系列が定常状態に収束することを意味します。一方で、1つでも根の絶対値が1以下である場合、モデルは不安定とされ、予測値が発散する可能性があります。すべての絶対値は１より大きいので安定していると言えます。

AutoRegは、OLSと同じ共分散推定器をサポートしています。以下では、Whiteの共分散推定量であるcov_type="HC0 "を使用します。パラメータ推定値は同じですが、標準誤差に依存する量はすべて変化します。

res = mod.fit(cov_type="HC0")
print(res.summary())

実際に標準誤差(std err)、z、p値、信頼区間に変化が見られますが、結論を変えるほどではありません。

次のセルのar_select_order 関数と sel.ar_lags 属性について解説します。

ar_select_order は、自己回帰（AR）モデルにおいて、どのラグ（遅れ）の数が最適であるかを選択するための関数です。これは、時系列データの以前の値が将来の値にどの程度影響を与えるかを分析する際に使用されます。この関数は以下のパラメータを取ります：

• data: 時系列データ
• maxlag: 考慮される最大のラグ数
• old_names: 旧バージョンの出力名を使用するかどうか

例えば、ar_select_order(housing, 13, old_names=False) というコードは、housing データセットに対して最大13のラグを考慮して、最適なラグ数を選択します。old_names=False は、新しい出力名を使用することを意味します。

sel.ar_lags は、ar_select_order によって返されるオブジェクトの属性で、選択された最適なラグのリストを提供します。この属性は、最適と判断された特定のラグ数を示し、そのラグが自己回帰モデルでどのように使用されるかを決定します。

sel = ar_select_order(housing, 13, old_names=False)
sel.ar_lags

sel.ar_lagsが[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]` を返しているので、これは時系列データにおいて1期前から13期前までのデータが現在の値を予測するのに最適であることを意味しています。この情報をもとに、自己回帰モデルはこれらのラグを使用して時系列データの将来の値を予測します。

res = sel.model.fit()
print(res.summary())

＊最初のモデル（AutoReg(3)）＊

1. 依存変数: HOUSTNSA。

2. 観測数: 778。

3. モデル: AutoReg(3)。3つのラグを使用。

4. AIC, BIC, HQIC: これらの値はモデルの適合度を示します。数値が小さいほど良い。

5. 係数:

   • const: 1.0998（定数項）。
   • HOUSTNSA.L1: 0.1835。
   • HOUSTNSA.L2: 0.0080。
   • HOUSTNSA.L3: -0.1950。

6. ルーツ: すべてのルーツの絶対値が1以上で、モデルは安定しています。

＊第二のモデル（AutoReg(13)）＊

1. 依存変数: HOUSTNSA。
2. 観測数: 778。
3. モデル: AutoReg(13)。13つのラグを使用。
4. AIC, BIC, HQIC: 最初のモデルより数値が小さいため、このモデルの方が適合度が高いと考えられます。
5. 係数: 13個のラグに対する係数があり、それぞれの影響力が示されています。
6. ルーツ: こちらのモデルもすべてのルーツの絶対値が1以上で、安定しています。

＊総合的な解釈＊

• 第二のモデル（AutoReg(13)）は、より多くのラグを使用しており、AIC, BIC, HQICの値が低いため、最初のモデル（AutoReg(3)）よりも適合度が高いと考えられます。
• 両モデルとも安定していますが、第二のモデルがより複雑な時系列のダイナミクスを捉えている可能性があります。
• 係数の値やその統計的有意性（P>|z|の値）を見ると、特定のラグが時系列にどのような影響を与えているかがわかります。例えば、AutoReg(13)モデルでは、HOUSTNSA.L12の係数が大きく、また統計的にも有意です。これは、12期前の値が現在の値に大きな影響を与えていることを示しています。

plot_predictは予測を可視化します。ここでは、モデルによって捕捉された文字列の季節性を示す多数の予測を生成しています。

AutoRegResults.plot_predict(start=None, end=None, dynamic=False, exog=None, exog_oos=None, alpha=0.05, in_sample=True, fig=None, figsize=None)[source]¶

fig = res.plot_predict(len(housing)-5, len(housing)-5+120)

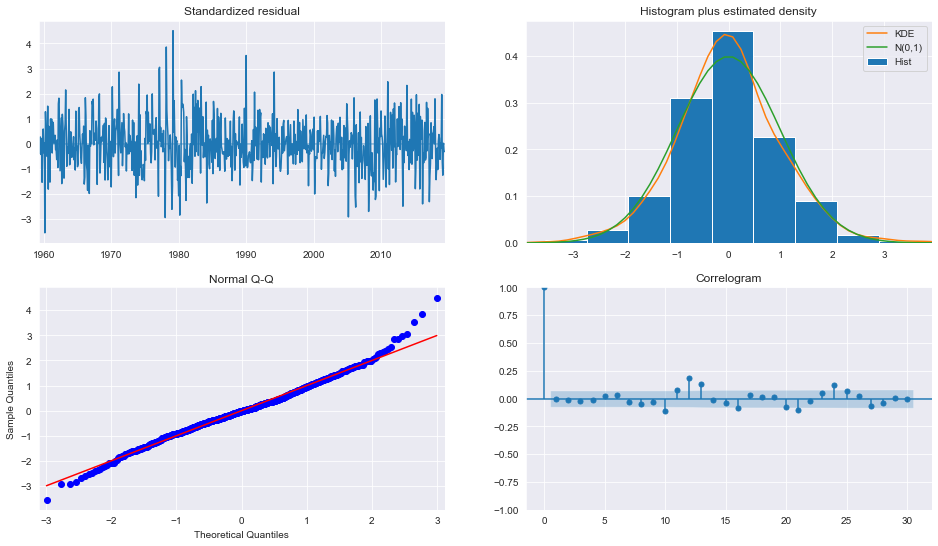
plot_diagnositcsは、モデルがデータの主要な特徴を捉えていることを示します。

fig = plt.figure(figsize=(16,9))
fig = res.plot_diagnostics(fig=fig, lags=30)

＊季節ダミー＊

AutoRegは季節ダミーもサポートしており、これは季節性をモデル化する別の方法です。ダミーを含めると、ダイナミクスがAR(2)に短縮されます。

sel = ar_select_order(housing, 13, seasonal=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())

季節ダミーは、特定の時期（通常は月や四半期）の周期的なパターンを捉えるために使用される変数です。これらの変数は、時系列データが示す季節性の影響をモデル化するために用いられます。たとえば、月次データの場合、各月に対応する12個の季節ダミー変数があり、その月が該当する場合は1、そうでない場合は0の値を取ります。

自己回帰モデルのラグ数を13に指定しましたが、季節ダミーを含めることで、モデルのダイナミクスが変わり、必要なラグの数が減少しました。この場合の「Seas. AutoReg(2)」モデルでは、季節ダミーを含めることにより、最適なラグの数が2つに減少しています。これは、季節ダミーが一部の季節性の影響を捉えるため、それ以外の自己回帰のラグの数を減らすことができるからです。

このモデルでは、季節ダミーが季節性の影響を担い、自己回帰の2つのラグが時系列の他のダイナミクスを捉える役割を果たしています。

＊基本情報＊

• 依存変数（Dep. Variable）: HOUSTNSA。分析対象の時系列データ。
• 観測数（No. Observations）: 778。データの観測点の数。
• モデル（Model）: Seas. AutoReg(2)。季節性を考慮した自己回帰モデルで、2つのラグ（遅れ）を使用。
• 方法（Method）: Conditional MLE（条件付き最尤推定法）。
• 標準偏差（S.D. of innovations）: 9.487。モデルの誤差項の標準偏差。
• AIC, BIC, HQIC: モデルの適合度を示す情報基準。数値が小さいほど良い。

＊係数とその統計＊

• const: 定数項の係数（1.2726）。
• s(2,12), s(3,12), ..., s(12,12): これらは季節ダミー変数の係数で、それぞれ異なる月に対応します（例：s(2,12)は2月、s(3,12)は3月）。これらの係数は季節性の影響を示しており、時系列データに特定の月がどのように影響するかを表します。
• HOUSTNSA.L1, HOUSTNSA.L2: 1期前と2期前のHOUSTNSAの係数。これらは自己回帰の部分で、過去の値が現在の値にどのように影響するかを示します。

＊根(Roots)＊

• モデルの「根」は、その動的特性を示します。この場合、2つの複素数の根があり、両方とも単位円の外側にあるため、モデルは安定しています。

＊総合的な解釈＊

このモデルは、HOUSTNSAデータにおける季節性の影響を明確に捉えています。季節ダミー変数の係数は、特定の月がデータに与える影響の大きさと方向を示しており、これらの係数が統計的に有意であるかどうかは、P>|z|の値で確認できます。また、自己回帰部分（HOUSTNSA.L1とL2）も時系列データの過去の値が現在の値に与える影響を示しており、こちらも統計的に有意な係数となっています。全体として、このモデルは季節性と過去のデータポイントの影響を同時に考慮して、HOUSTNSAの動向を分析しています。

つぎに、季節ダミーは予測において有効なので、今後10年間のすべての期間において季節成分として取り入れます。

fig = res.plot_predict(len(housing)-5, len(housing)-5+120)

fig = plt.figure(figsize=(16,9))
fig = res.plot_diagnostics(lags=30, fig=fig)

＊季節ダイナミクス＊

AutoRegはOLS（最小二乗法）を使用してパラメータを推定するため、直接的に季節成分をサポートしていませんが、季節ARの制約を課さない過剰パラメータ化された季節ARを使用することで、季節ダイナミクスを捉えることが可能です。

過剰パラメータ化された季節自己回帰（Seasonal AR）モデルとは、通常の季節自己回帰モデルにおける一般的な制約を設けずに、多数のパラメータを用いて季節性のダイナミクスをモデル化するアプローチです。ここでの「制約を課さない」というのは、モデルが季節的な変動を捉えるために通常適用される特定の数学的な制約や仮定を用いず、より多くのパラメータを使用することを意味します。

季節ARモデルでは通常、特定の周期（例えば、月次データの12ヶ月周期）に基づいてラグを選択し、それらのラグの係数を推定します。このモデルは、季節性が特定の周期で繰り返されるという仮定に基づいています。

過剰パラメータ化された季節ARモデルでは、より多くのラグを使用し、季節性をより柔軟に捉えます。このアプローチでは、通常の季節ARモデルよりも多くのラグを用いて季節性の各側面を詳細にモデル化し、季節性のより微細な変動を捉えることができます。

この方法は、特に季節パターンが単純な年次周期に収まらない複雑な時系列データに有効です。しかし、過剰パラメータ化によってモデルが過学習（過剰適合）を起こすリスクも高まるため、注意深いモデル選択とパラメータの評価が必要です。

yoy_housing = data.HOUSTNSA.pct_change(12).resample("MS").last().dropna()

上述の、data.HOUSTNSA.pct_change(12) は data.HOUSTNSA 時系列データの各点で、その12ヶ月前の値と比較してどれだけ変化したか（パーセンテージで）を計算します。これにより、年次ベースでの成長率や減少率などを分析することができます。

resample("MS").last() はデータを月初（"MS" = month start）に再サンプリングし、各月の最後の観測値を使用することを意味します。そして、dropna() により欠損値が除去されます。

このコードは、HOUSTNSA データセットの年間パーセンテージ変化を月次でプロットするためのものです。

yoy_housing = data.HOUSTNSA.pct_change(12).resample("MS").last().dropna()
_, ax = plt.subplots()
ax = yoy_housing.plot(ax=ax)

最大ラグを選択するだけのシンプルな方法を用いてモデルの選択を始めます。全ての低いラグが自動的に含まれます。最大ラグは13に設定されており、これによりモデルは短期のAR(1)成分と季節性AR(1)成分の両方を持つ季節性ARを考慮することができます。すなわち、

$$ (1-\phi_sL^{12})(1-\phi_1L)y_t=\epsilon_t$$

これは展開すると

$$y_t=\phi_1y_{t-1}+\phi_{s}Y_{t-12}-\phi_{s}Y_{t-13}+\epsilon_t$$

となります。(大文字は最終的に選択されたラグ) AutoRegはこの構造を強制しませんが、入れ子型のモデル

$$y_t=\phi_1y_{t-1}+\phi_{12}Y_{t-12}-\phi_{13}Y_{t-13}+\epsilon_t$$

を推定することができます。

ここでは全13のラグが選択されていることが分かります。

sel = ar_select_order(yoy_housing, 13, old_names=False)
sel.ar_lags
#
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13])

すべての13のラグが必要とは思えません。最大13のラグを含む全ての $2^{13}$ モデルを検索するために、glob=Trueを設定することができます。

ここで、最初の3つが選択され、そして最終的に12番目と13番目が選択されていることが分かります。これは上述の構造と表面的には似ています。

モデルを適用した後、データのダイナミクスを捉えるためにこの仕様が適切であることを示す診断プロットを見てみましょう。

sel = ar_select_order(yoy_housing, 13, glob=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())

#

提供されたAutoRegモデルのサマリーレポートは、13次の制約付き自己回帰（AutoRegressive）モデルの結果を示しています。このモデルでは、13のラグ（遅延）が考慮されており、それらの中で特定のラグ（L1, L2, L3, L12, L13）に対する係数が有意であると判断されています。

モデルのサマリーに含まれる「Roots」セクションは、モデルの特性方程式の根（ルーツ）を示しています。これらの根はモデルの安定性や振る舞いを理解するのに重要です。ARモデルでは、これらの根はモデルのラグ多項式の根として計算されます。

ARモデルの13次までの「モジュラス」が表示されている理由は、モデルが13次の自己回帰成分を持つためです。モデルに含まれるすべてのラグに対応する根（ルーツ）が計算され、それらの根のモジュラス（絶対値）が表示されます。

係数が有意なラグ（L1, L2, L3, L12, L13）がモデルにおいて重要な役割を果たしていることを示していますが、モデルの安定性や振る舞いを理解するためには、すべてのラグに対応する根を考慮することが重要です。これらの根は、モデルがどのように時系列データの過去の値に依存するか、また時間とともにどのように挙動するかを示します。

したがって、特定のラグの係数が有意であっても、モデルの全体的な挙動を理解するためには、すべてのラグに対応する根を検討する必要があります。

fig = plt.figure(figsize=(16,9))
fig = res.plot_diagnostics(fig=fig, lags=30)

季節的なダミーも含めることができます。モデルは前年比変化を使用しているので、これらはすべて有意ではありません。

sel = ar_select_order(yoy_housing, 13, glob=True, seasonal=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())

import numpy as np

start = yoy_housing.index[-6]
forecast_index = pd.date_range(start, freq=yoy_housing.index.freq, periods=12)
cols = ["-".join(str(val) for val in (idx.year, idx.month)) for idx in forecast_index]
forecasts = pd.DataFrame(index=forecast_index, columns=cols)
for i in range(1, 6):
    fcast = res.predict(
        start=forecast_index[i], end=forecast_index[i + 6], dynamic=True
    )
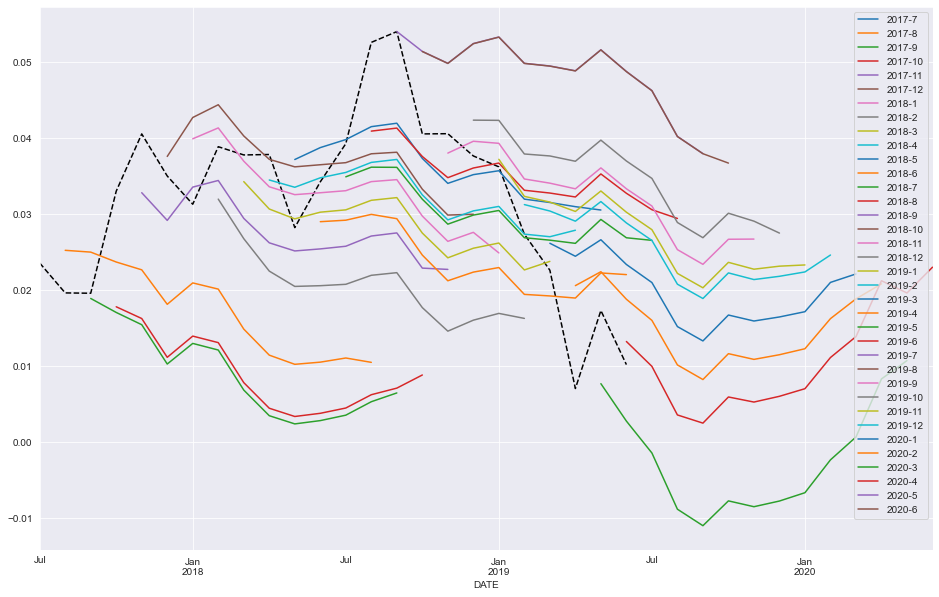
    forecasts.loc[fcast.index, cols[i]] = fcast
_, ax = plt.subplots(figsize=(8, 4))
#yoy_housing.iloc[-6:].plot(ax=ax, color="black", linestyle="--")
ax = forecasts.plot(ax=ax)

工業生産

工業生産指数データを用いて予測を検討します。

data = pdr.get_data_fred('INDPRO', '1959-01-01', '2019-06-01')
ind_prod = data.INDPRO.pct_change(12).dropna().asfreq('MS')
_, ax = plt.subplots(figsize=(16,9))
ind_prod.plot(ax=ax)

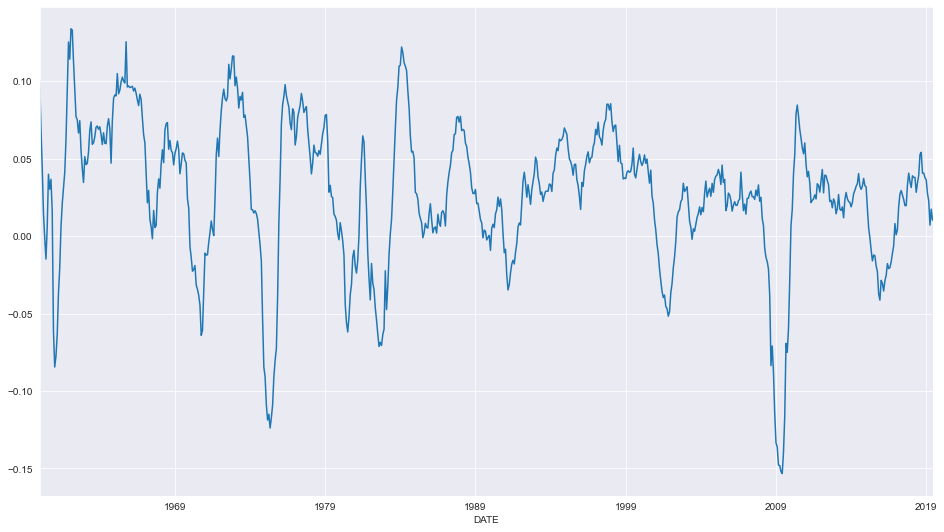
最大12のラグを使用するモデルを選択することから始めます。AR(13) は、多くの係数が取るに足らないものであっても、BIC 基準を最小化します。

sel = ar_select_order(ind_prod, 13, 'bic', old_names=False)
res = sel.model.fit()
print(res.summary())
"
AutoReg Model Results                             
==============================================================================
Dep. Variable:                 INDPRO   No. Observations:                  714
Model:                    AutoReg(13)   Log Likelihood                2318.848
Method:               Conditional MLE   S.D. of innovations              0.009
Date:                Tue, 23 Feb 2021   AIC                             -9.411
Time:                        14:08:08   BIC                             -9.313
Sample:                    02-01-1961   HQIC                            -9.373
                         - 06-01-2019                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.0012      0.000      2.896      0.004       0.000       0.002
INDPRO.L1      1.1504      0.035     32.940      0.000       1.082       1.219
INDPRO.L2     -0.0747      0.053     -1.407      0.159      -0.179       0.029
INDPRO.L3      0.0043      0.053      0.081      0.935      -0.099       0.107
INDPRO.L4      0.0027      0.053      0.052      0.959      -0.100       0.106
INDPRO.L5     -0.1383      0.052     -2.642      0.008      -0.241      -0.036
INDPRO.L6      0.0085      0.052      0.163      0.871      -0.094       0.111
INDPRO.L7      0.0375      0.052      0.720      0.471      -0.065       0.139
INDPRO.L8     -0.0235      0.052     -0.453      0.651      -0.125       0.078
INDPRO.L9      0.0945      0.052      1.824      0.068      -0.007       0.196
INDPRO.L10    -0.0844      0.052     -1.627      0.104      -0.186       0.017
INDPRO.L11     0.0024      0.052      0.047      0.962      -0.099       0.104
INDPRO.L12    -0.3809      0.052     -7.367      0.000      -0.482      -0.280
INDPRO.L13     0.3589      0.033     10.916      0.000       0.294       0.423
                                    Roots                                     
==============================================================================
                   Real          Imaginary           Modulus         Frequency
------------------------------------------------------------------------------
AR.1            -1.0411           -0.2889j            1.0804           -0.4569
AR.2            -1.0411           +0.2889j            1.0804            0.4569
AR.3            -0.7774           -0.8064j            1.1201           -0.3721
AR.4            -0.7774           +0.8064j            1.1201            0.3721
AR.5            -0.2760           -1.0530j            1.0886           -0.2908
AR.6            -0.2760           +1.0530j            1.0886            0.2908
AR.7             0.2719           -1.0515j            1.0861           -0.2097
AR.8             0.2719           +1.0515j            1.0861            0.2097
AR.9             0.8019           -0.7297j            1.0842           -0.1175
AR.10            0.8019           +0.7297j            1.0842            0.1175
AR.11            1.0224           -0.2214j            1.0461           -0.0339
AR.12            1.0224           +0.2214j            1.0461            0.0339
AR.13            1.0578           -0.0000j            1.0578           -0.0000
------------------------------------------------------------------------------

また、短いラグを必要とせずに、必要に応じてより長いラグを入力できるグローバル検索を使用することもできます。ここでは、多くのラグが削除されているのがわかります。このモデルは、データに季節性があるかもしれないことを示しています。

sel = ar_select_order(ind_prod, 13, 'bic', glob=True, old_names=False)
sel.ar_lags
res_glob = sel.model.fit()
print(res.summary())
#
 AutoReg Model Results                             
==============================================================================
Dep. Variable:                 INDPRO   No. Observations:                  714
Model:                    AutoReg(13)   Log Likelihood                2318.848
Method:               Conditional MLE   S.D. of innovations              0.009
Date:                Tue, 23 Feb 2021   AIC                             -9.411
Time:                        14:08:26   BIC                             -9.313
Sample:                    02-01-1961   HQIC                            -9.373
                         - 06-01-2019                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.0012      0.000      2.896      0.004       0.000       0.002
INDPRO.L1      1.1504      0.035     32.940      0.000       1.082       1.219
INDPRO.L2     -0.0747      0.053     -1.407      0.159      -0.179       0.029
INDPRO.L3      0.0043      0.053      0.081      0.935      -0.099       0.107
INDPRO.L4      0.0027      0.053      0.052      0.959      -0.100       0.106
INDPRO.L5     -0.1383      0.052     -2.642      0.008      -0.241      -0.036
INDPRO.L6      0.0085      0.052      0.163      0.871      -0.094       0.111
INDPRO.L7      0.0375      0.052      0.720      0.471      -0.065       0.139
INDPRO.L8     -0.0235      0.052     -0.453      0.651      -0.125       0.078
INDPRO.L9      0.0945      0.052      1.824      0.068      -0.007       0.196
INDPRO.L10    -0.0844      0.052     -1.627      0.104      -0.186       0.017
INDPRO.L11     0.0024      0.052      0.047      0.962      -0.099       0.104
INDPRO.L12    -0.3809      0.052     -7.367      0.000      -0.482      -0.280
INDPRO.L13     0.3589      0.033     10.916      0.000       0.294       0.423
                                    Roots                                     
==============================================================================
                   Real          Imaginary           Modulus         Frequency
------------------------------------------------------------------------------
AR.1            -1.0411           -0.2889j            1.0804           -0.4569
AR.2            -1.0411           +0.2889j            1.0804            0.4569
AR.3            -0.7774           -0.8064j            1.1201           -0.3721
AR.4            -0.7774           +0.8064j            1.1201            0.3721
AR.5            -0.2760           -1.0530j            1.0886           -0.2908
AR.6            -0.2760           +1.0530j            1.0886            0.2908
AR.7             0.2719           -1.0515j            1.0861           -0.2097
AR.8             0.2719           +1.0515j            1.0861            0.2097
AR.9             0.8019           -0.7297j            1.0842           -0.1175
AR.10            0.8019           +0.7297j            1.0842            0.1175
AR.11            1.0224           -0.2214j            1.0461           -0.0339
AR.12            1.0224           +0.2214j            1.0461            0.0339
AR.13            1.0578           -0.0000j            1.0578           -0.0000
------------------------------------------------------------------------------

plot_predictは、信頼区間とともに予測プロットを作成します。ここでは、最後の観測から始まり、18ヶ月間の予測を作成しています。

ind_prod.shape
#
(714,)

fig = res_glob.plot_predict(start=714, end=732)

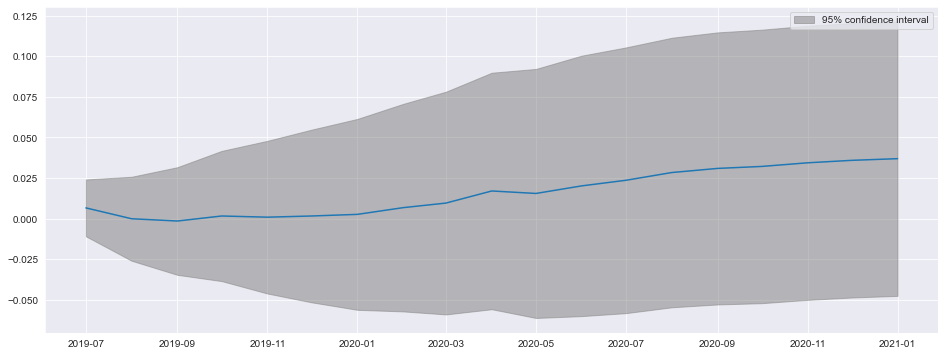
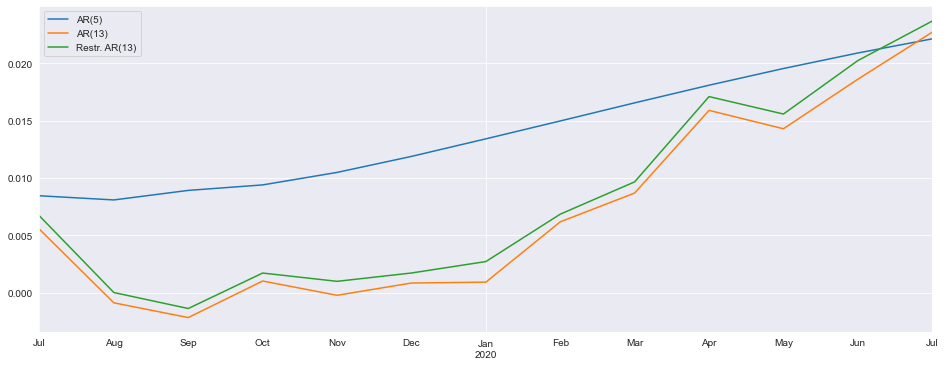
フルモデルと制限モデルからの予測は非常によく似ています。また、非常に異なるダイナミクスを持つAR(5)も含みます。

res_ar5 = AutoReg(ind_prod, 5, old_names=False).fit()
predictions = pd.DataFrame({"AR(5)": res_ar5.predict(start=714, end=726),
                            "AR(13)": res.predict(start=714, end=726),
                            "Restr. AR(13)": res_glob.predict(start=714, end=726)})
_, ax = plt.subplots()
ax = predictions.plot(ax=ax)

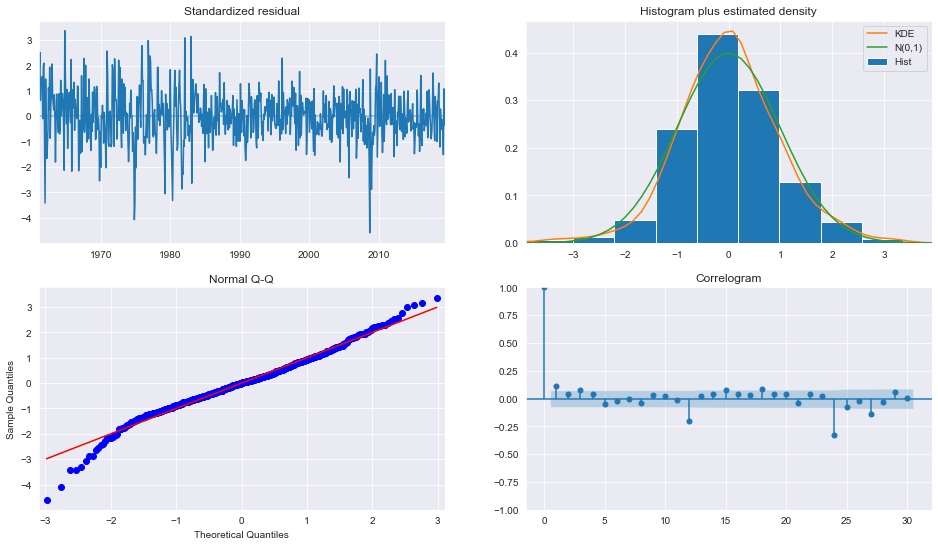
診断は、モデルがデータのダイナミクスの大部分を捉えていることを示しています。ACFは季節周波数でのパターンを示しているので、より完全な季節モデル(SARIMAX)が必要かもしれません。

fig = plt.figure(figsize=(16,9))
fig = res_glob.plot_diagnostics(fig=fig, lags=30)

予測

予測は、結果のインスタンスから predict メソッドを使用して生成されます。デフォルトでは、静的な予測が生成され、これはワンステップ予測です。マルチステップ予測を作成するには、dynamic=Trueを使用する必要があります。

この次のセルでは、サンプルの最後の24期間の12段階の予測を作成します。これにはループが必要です。

注意：これらは、我々が予測しているデータがパラメータを推定するために使用されたので、技術的にはインサンプルです。OOS予測を作成するには、2つのモデルが必要です。1つ目は、OOS期間を除外しなければなりません。2つ目は、OOS期間を除外した短いサンプル・モデルのパラメータを用いて、フル・サンプル・モデルからの予測法を使用します。

import numpy as np
start = ind_prod.index[-24]
forecast_index = pd.date_range(start, freq=ind_prod.index.freq, periods=36)
cols = ['-'.join(str(val) for val in (idx.year, idx.month)) for idx in forecast_index]
forecasts = pd.DataFrame(index=forecast_index,columns=cols)
for i in range(1, 24):
    fcast = res_glob.predict(start=forecast_index[i], end=forecast_index[i+12], dynamic=True)
    forecasts.loc[fcast.index, cols[i]] = fcast
_, ax = plt.subplots(figsize=(16, 10))
ind_prod.iloc[-24:].plot(ax=ax, color="black", linestyle="--")
ax = forecasts.plot(ax=ax)

SARIMAXとの比較

SARIMAXは、eXogenous regressorsモデルを用いた季節自己回帰統合移動平均の実装です。SARIMAXは以下をサポートしています。

• 季節的および非季節的なARおよびMA成分の指定

• 外生変数を含める

• カルマンフィルタを用いた完全最尤推定

このモデルはAutoRegよりも特徴が豊富です。SARIMAXとは異なり、AutoRegはOLSを用いてパラメータを推定します。これはより高速であり、問題は大域的に凸であるため、局所的なミニマの問題はありません。AR(P)モデルを比較する際に、閉形式推定器とその性能がSARIMAXに対するAutoRegの主な利点となります。AutoRegは季節ダミーもサポートしており、ユーザーが外生的回帰子としてそれらを含める場合、SARIMAXと一緒に使用することができます。

from statsmodels.tsa.api import SARIMAX

sarimax_mod = SARIMAX(ind_prod, order=((1,5,12,13),0, 0), trend='c')
sarimax_res = sarimax_mod.fit()
print(sarimax_res.summary())
#
SARIMAX Results                                     
=========================================================================================
Dep. Variable:                            INDPRO   No. Observations:                  714
Model:             SARIMAX([1, 5, 12, 13], 0, 0)   Log Likelihood                2302.146
Date:                           Tue, 23 Feb 2021   AIC                          -4592.293
Time:                                   14:10:42   BIC                          -4564.867
Sample:                               01-01-1960   HQIC                         -4581.701
                                    - 06-01-2019                                         
Covariance Type:                             opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
intercept      0.0011      0.000      2.627      0.009       0.000       0.002
ar.L1          1.0798      0.010    106.388      0.000       1.060       1.100
ar.L5         -0.0849      0.011     -7.467      0.000      -0.107      -0.063
ar.L12        -0.4392      0.026    -16.935      0.000      -0.490      -0.388
ar.L13         0.4032      0.025     15.831      0.000       0.353       0.453
sigma2      9.179e-05   3.13e-06     29.366      0.000    8.57e-05    9.79e-05
===================================================================================
Ljung-Box (L1) (Q):                  19.65   Jarque-Bera (JB):               928.85
Prob(Q):                              0.00   Prob(JB):                         0.00
Heteroskedasticity (H):               0.38   Skew:                            -0.63
Prob(H) (two-sided):                  0.00   Kurtosis:                         8.44
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

sarimax_params = sarimax_res.params.iloc[:-1].copy()
sarimax_params.index = res_glob.params.index
params = pd.concat([res_glob.params, sarimax_params], axis=1, sort=False)
params.columns = ["AutoReg", "SARIMAX"]
params
#
AutoReg	SARIMAX
const	0.001292	0.001140
INDPRO.L1	1.088215	1.079829
INDPRO.L5	-0.105668	-0.084904
INDPRO.L12	-0.385171	-0.439175
INDPRO.L13	0.358738	0.403241

カスタム決定論的プロセス

決定論的パラメータは、自由に決定論的プロセスを作成することを可能にします。これにより、より複雑な決定論的項を構築することができます。例えば、2つの期間を持つ季節成分を含むものや、次の例が示すように、季節ダミーではなくフーリエ級数を使用するものなどがあります。

from statsmodels.tsa.deterministic import DeterministicProcess
dp = DeterministicProcess(housing.index, constant=True, period=12, fourier=2)
mod = AutoReg(housing,2, trend="n",seasonal=False, deterministic=dp)
res = mod.fit()
print(res.summary())
#
 AutoReg Model Results                             
==============================================================================
Dep. Variable:               HOUSTNSA   No. Observations:                  725
Model:                     AutoReg(2)   Log Likelihood               -2716.505
Method:               Conditional MLE   S.D. of innovations             10.364
Date:                Tue, 23 Feb 2021   AIC                              4.699
Time:                        14:11:45   BIC                              4.750
Sample:                    04-01-1959   HQIC                             4.718
                         - 06-01-2019                                         
===============================================================================
                  coef    std err          z      P>|z|      [0.025      0.975]
-------------------------------------------------------------------------------
const           1.7550      0.391      4.485      0.000       0.988       2.522
sin(1,12)      16.7443      0.860     19.478      0.000      15.059      18.429
cos(1,12)       4.9409      0.588      8.409      0.000       3.789       6.093
sin(2,12)      12.9364      0.619     20.889      0.000      11.723      14.150
cos(2,12)      -0.4738      0.754     -0.628      0.530      -1.952       1.004
HOUSTNSA.L1    -0.3905      0.037    -10.664      0.000      -0.462      -0.319
HOUSTNSA.L2    -0.1746      0.037     -4.769      0.000      -0.246      -0.103
                                    Roots                                    
=============================================================================
                  Real          Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1           -1.1182           -2.1159j            2.3932           -0.3274
AR.2           -1.1182           +2.1159j            2.3932            0.3274
-----------------------------------------------------------------------------

fig = res.plot_predict(720, 840)
fig = res.plot_predict(720, 840)

確定的トレンド

基本的な使い方

基本的な構成は DeterministicProcess を通して直接構築することができます。これらは、定数、任意の順序の時間トレンド、季節成分またはフーリエ成分で構成されます。

プロセスは、フルサンプル（またはインサンプル）のインデックスを必要とします。

まず、定数、線形時間トレンド、5周期の季節項を持つ決定論的プロセスを初期化します。in_sampleメソッドは、インデックスに一致する値の完全集合を返します。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

plt.rc("figure", figsize=(16, 9))
plt.rc("font", size=16)

from statsmodels.tsa.deterministic import DeterministicProcess

index = pd.RangeIndex(0, 100)
det_proc = DeterministicProcess(
    index, constant=True, order=1, seasonal=True, period=5
)
det_proc.in_sample()
#
const	trend	s(2,5)	s(3,5)	s(4,5)	s(5,5)
0	1.0	1.0	0.0	0.0	0.0	0.0
1	1.0	2.0	1.0	0.0	0.0	0.0
2	1.0	3.0	0.0	1.0	0.0	0.0
3	1.0	4.0	0.0	0.0	1.0	0.0
4	1.0	5.0	0.0	0.0	0.0	1.0
...	...	...	...	...	...	...
95	1.0	96.0	0.0	0.0	0.0	0.0
96	1.0	97.0	1.0	0.0	0.0	0.0
97	1.0	98.0	0.0	1.0	0.0	0.0
98	1.0	99.0	0.0	0.0	1.0	0.0
99	1.0	100.0	0.0	0.0	0.0	1.0
100 rows × 6 columns

out_of_sample は、インサンプル終了後の次のステップの値を返します。

det_proc.out_of_sample(15)
#
const	trend	s(2,5)	s(3,5)	s(4,5)	s(5,5)
100	1.0	101.0	0.0	0.0	0.0	0.0
101	1.0	102.0	1.0	0.0	0.0	0.0
102	1.0	103.0	0.0	1.0	0.0	0.0
103	1.0	104.0	0.0	0.0	1.0	0.0
104	1.0	105.0	0.0	0.0	0.0	1.0
105	1.0	106.0	0.0	0.0	0.0	0.0
106	1.0	107.0	1.0	0.0	0.0	0.0
107	1.0	108.0	0.0	1.0	0.0	0.0
108	1.0	109.0	0.0	0.0	1.0	0.0
109	1.0	110.0	0.0	0.0	0.0	1.0
110	1.0	111.0	0.0	0.0	0.0	0.0
111	1.0	112.0	1.0	0.0	0.0	0.0
112	1.0	113.0	0.0	1.0	0.0	0.0
113	1.0	114.0	0.0	0.0	1.0	0.0
114	1.0	115.0	0.0	0.0	0.0	1.0

range(start, stop) は、サンプル内およびサンプル外を含む任意の範囲の決定論的項を生成するために使用できます。

注意事項

インデックスがpandas DatetimeIndexまたはPeriodIndexである場合、startとstopは日付的なもの(文字列、例えば "2020-06-01 "やTimestamp)でも整数でも構いません。

stopは常に範囲に含まれます。これはあまりPythonicなものではありませんが、statsmodelsとPandasの両方がデータライクなスライスを扱うときにstopを含むので必要です。

det_proc.range(190, 210)
#
const	trend	s(2,5)	s(3,5)	s(4,5)	s(5,5)
190	1.0	191.0	0.0	0.0	0.0	0.0
191	1.0	192.0	1.0	0.0	0.0	0.0
192	1.0	193.0	0.0	1.0	0.0	0.0
193	1.0	194.0	0.0	0.0	1.0	0.0
194	1.0	195.0	0.0	0.0	0.0	1.0
195	1.0	196.0	0.0	0.0	0.0	0.0
196	1.0	197.0	1.0	0.0	0.0	0.0
197	1.0	198.0	0.0	1.0	0.0	0.0
198	1.0	199.0	0.0	0.0	1.0	0.0
199	1.0	200.0	0.0	0.0	0.0	1.0
200	1.0	201.0	0.0	0.0	0.0	0.0
201	1.0	202.0	1.0	0.0	0.0	0.0
202	1.0	203.0	0.0	1.0	0.0	0.0
203	1.0	204.0	0.0	0.0	1.0	0.0
204	1.0	205.0	0.0	0.0	0.0	1.0
205	1.0	206.0	0.0	0.0	0.0	0.0
206	1.0	207.0	1.0	0.0	0.0	0.0
207	1.0	208.0	0.0	1.0	0.0	0.0
208	1.0	209.0	0.0	0.0	1.0	0.0
209	1.0	210.0	0.0	0.0	0.0	1.0
210	1.0	211.0	0.0	0.0	0.0	0.0

日付のインデックス

次に、PeriodIndexを使って同じ手順を示します。

index = pd.period_range("2020-03-01", freq="M", periods=60)
det_proc = DeterministicProcess(index, constant=True, fourier=2)
det_proc.in_sample().head(12)
#
const	sin(1,12)	cos(1,12)	sin(2,12)	cos(2,12)
2020-03	1.0	0.000000e+00	1.000000e+00	0.000000e+00	1.0
2020-04	1.0	5.000000e-01	8.660254e-01	8.660254e-01	0.5
2020-05	1.0	8.660254e-01	5.000000e-01	8.660254e-01	-0.5
2020-06	1.0	1.000000e+00	6.123234e-17	1.224647e-16	-1.0
2020-07	1.0	8.660254e-01	-5.000000e-01	-8.660254e-01	-0.5
2020-08	1.0	5.000000e-01	-8.660254e-01	-8.660254e-01	0.5
2020-09	1.0	1.224647e-16	-1.000000e+00	-2.449294e-16	1.0
2020-10	1.0	-5.000000e-01	-8.660254e-01	8.660254e-01	0.5
2020-11	1.0	-8.660254e-01	-5.000000e-01	8.660254e-01	-0.5
2020-12	1.0	-1.000000e+00	-1.836970e-16	3.673940e-16	-1.0
2021-01	1.0	-8.660254e-01	5.000000e-01	-8.660254e-01	-0.5
2021-02	1.0	-5.000000e-01	8.660254e-01	-8.660254e-01	0.5

det_proc.out_of_sample(12)
#
const	sin(1,12)	cos(1,12)	sin(2,12)	cos(2,12)
2025-03	1.0	-1.224647e-15	1.000000e+00	-2.449294e-15	1.0
2025-04	1.0	5.000000e-01	8.660254e-01	8.660254e-01	0.5
2025-05	1.0	8.660254e-01	5.000000e-01	8.660254e-01	-0.5
2025-06	1.0	1.000000e+00	-4.904777e-16	-9.809554e-16	-1.0
2025-07	1.0	8.660254e-01	-5.000000e-01	-8.660254e-01	-0.5
2025-08	1.0	5.000000e-01	-8.660254e-01	-8.660254e-01	0.5
2025-09	1.0	4.899825e-15	-1.000000e+00	-9.799650e-15	1.0
2025-10	1.0	-5.000000e-01	-8.660254e-01	8.660254e-01	0.5
2025-11	1.0	-8.660254e-01	-5.000000e-01	8.660254e-01	-0.5
2025-12	1.0	-1.000000e+00	-3.184701e-15	6.369401e-15	-1.0
2026-01	1.0	-8.660254e-01	5.000000e-01	-8.660254e-01	-0.5
2026-02	1.0	-5.000000e-01	8.660254e-01	-8.660254e-01	0.5

rangeは、通常は文字列として与えられる日付の引数を受け付けます。

det_proc.range("2025-01", "2026-01")
#
const	sin(1,12)	cos(1,12)	sin(2,12)	cos(2,12)
2025-01	1.0	-8.660254e-01	5.000000e-01	-8.660254e-01	-0.5
2025-02	1.0	-5.000000e-01	8.660254e-01	-8.660254e-01	0.5
2025-03	1.0	-1.224647e-15	1.000000e+00	-2.449294e-15	1.0
2025-04	1.0	5.000000e-01	8.660254e-01	8.660254e-01	0.5
2025-05	1.0	8.660254e-01	5.000000e-01	8.660254e-01	-0.5
2025-06	1.0	1.000000e+00	-4.904777e-16	-9.809554e-16	-1.0
2025-07	1.0	8.660254e-01	-5.000000e-01	-8.660254e-01	-0.5
2025-08	1.0	5.000000e-01	-8.660254e-01	-8.660254e-01	0.5
2025-09	1.0	4.899825e-15	-1.000000e+00	-9.799650e-15	1.0
2025-10	1.0	-5.000000e-01	-8.660254e-01	8.660254e-01	0.5
2025-11	1.0	-8.660254e-01	-5.000000e-01	8.660254e-01	-0.5
2025-12	1.0	-1.000000e+00	-3.184701e-15	6.369401e-15	-1.0
2026-01	1.0	-8.660254e-01	5.000000e-01	-8.660254e-01	-0.5

これは、整数値５８と整数値７０を使用してもできます。

det_proc.range(58, 70)
#
const	sin(1,12)	cos(1,12)	sin(2,12)	cos(2,12)
2025-01	1.0	-8.660254e-01	5.000000e-01	-8.660254e-01	-0.5
2025-02	1.0	-5.000000e-01	8.660254e-01	-8.660254e-01	0.5
2025-03	1.0	-1.224647e-15	1.000000e+00	-2.449294e-15	1.0
2025-04	1.0	5.000000e-01	8.660254e-01	8.660254e-01	0.5
2025-05	1.0	8.660254e-01	5.000000e-01	8.660254e-01	-0.5
2025-06	1.0	1.000000e+00	-4.904777e-16	-9.809554e-16	-1.0
2025-07	1.0	8.660254e-01	-5.000000e-01	-8.660254e-01	-0.5
2025-08	1.0	5.000000e-01	-8.660254e-01	-8.660254e-01	0.5
2025-09	1.0	4.899825e-15	-1.000000e+00	-9.799650e-15	1.0
2025-10	1.0	-5.000000e-01	-8.660254e-01	8.660254e-01	0.5
2025-11	1.0	-8.660254e-01	-5.000000e-01	8.660254e-01	-0.5
2025-12	1.0	-1.000000e+00	-3.184701e-15	6.369401e-15	-1.0
2026-01	1.0	-8.660254e-01	5.000000e-01	-8.660254e-01	-0.5

コントラクタの作成

コンストラクタで直接サポートされていない決定論的プロセスは、 additional_terms を用いて DetermisticTerm のリストを受け取ることで作成できます。ここでは、2つの季節成分を持つ決定論的プロセスを作成しています: 5日間の期間を持つ曜日と、365.25日の期間を持つフーリエ成分で捕捉された年次です。

from statsmodels.tsa.deterministic import Fourier, Seasonality, TimeTrend

index = pd.period_range("2020-03-01", freq="D", periods=2 * 365)
tt = TimeTrend(constant=True)
four = Fourier(period=365.25, order=2)
seas = Seasonality(period=7)
det_proc = DeterministicProcess(index, additional_terms=[tt, seas, four])
det_proc.in_sample().head(28)
#
const	s(2,7)	s(3,7)	s(4,7)	s(5,7)	s(6,7)	s(7,7)	sin(1,365.25)	cos(1,365.25)	sin(2,365.25)	cos(2,365.25)
2020-03-01	1.0	0.0	0.0	0.0	0.0	0.0	0.0	0.000000	1.000000	0.000000	1.000000
2020-03-02	1.0	1.0	0.0	0.0	0.0	0.0	0.0	0.017202	0.999852	0.034398	0.999408
2020-03-03	1.0	0.0	1.0	0.0	0.0	0.0	0.0	0.034398	0.999408	0.068755	0.997634
2020-03-04	1.0	0.0	0.0	1.0	0.0	0.0	0.0	0.051584	0.998669	0.103031	0.994678
2020-03-05	1.0	0.0	0.0	0.0	1.0	0.0	0.0	0.068755	0.997634	0.137185	0.990545
2020-03-06	1.0	0.0	0.0	0.0	0.0	1.0	0.0	0.085906	0.996303	0.171177	0.985240
2020-03-07	1.0	0.0	0.0	0.0	0.0	0.0	1.0	0.103031	0.994678	0.204966	0.978769
2020-03-08	1.0	0.0	0.0	0.0	0.0	0.0	0.0	0.120126	0.992759	0.238513	0.971139
2020-03-09	1.0	1.0	0.0	0.0	0.0	0.0	0.0	0.137185	0.990545	0.271777	0.962360
2020-03-10	1.0	0.0	1.0	0.0	0.0	0.0	0.0	0.154204	0.988039	0.304719	0.952442
2020-03-11	1.0	0.0	0.0	1.0	0.0	0.0	0.0	0.171177	0.985240	0.337301	0.941397
2020-03-12	1.0	0.0	0.0	0.0	1.0	0.0	0.0	0.188099	0.982150	0.369484	0.929237
2020-03-13	1.0	0.0	0.0	0.0	0.0	1.0	0.0	0.204966	0.978769	0.401229	0.915978
2020-03-14	1.0	0.0	0.0	0.0	0.0	0.0	1.0	0.221772	0.975099	0.432499	0.901634
2020-03-15	1.0	0.0	0.0	0.0	0.0	0.0	0.0	0.238513	0.971139	0.463258	0.886224
2020-03-16	1.0	1.0	0.0	0.0	0.0	0.0	0.0	0.255182	0.966893	0.493468	0.869764
2020-03-17	1.0	0.0	1.0	0.0	0.0	0.0	0.0	0.271777	0.962360	0.523094	0.852275
2020-03-18	1.0	0.0	0.0	1.0	0.0	0.0	0.0	0.288291	0.957543	0.552101	0.833777
2020-03-19	1.0	0.0	0.0	0.0	1.0	0.0	0.0	0.304719	0.952442	0.580455	0.814292
2020-03-20	1.0	0.0	0.0	0.0	0.0	1.0	0.0	0.321058	0.947060	0.608121	0.793844
2020-03-21	1.0	0.0	0.0	0.0	0.0	0.0	1.0	0.337301	0.941397	0.635068	0.772456
2020-03-22	1.0	0.0	0.0	0.0	0.0	0.0	0.0	0.353445	0.935455	0.661263	0.750154
2020-03-23	1.0	1.0	0.0	0.0	0.0	0.0	0.0	0.369484	0.929237	0.686676	0.726964
2020-03-24	1.0	0.0	1.0	0.0	0.0	0.0	0.0	0.385413	0.922744	0.711276	0.702913
2020-03-25	1.0	0.0	0.0	1.0	0.0	0.0	0.0	0.401229	0.915978	0.735034	0.678031
2020-03-26	1.0	0.0	0.0	0.0	1.0	0.0	0.0	0.416926	0.908940	0.757922	0.652346
2020-03-27	1.0	0.0	0.0	0.0	0.0	1.0	0.0	0.432499	0.901634	0.779913	0.625889
2020-03-28	1.0	0.0	0.0	0.0	0.0	0.0	1.0	0.447945	0.894061	0.800980	0.598691

決定論的プロセスの作成

DetermisticTerm 抽象基底クラスは、ユーザーが自由に決定論的な項を書くのを助けるためにサブクラス化されています。次に2つの例を示します。1つ目は、一定の期間の後にブレークするブレークタイムトレンドです。2つ目は、決定論的なプロセスではない外生データを、あたかも決定論的であるかのように扱うことを可能にする、"トリック "な決定論的項です。これにより、予測に必要な項の生成を単純化することができます。

これらは、カスタム用語の構築を可能にすることを意図し、入力の妥当性の確認の点で間違いなく良い方向にモデリングの過程を導きます。

from statsmodels.tsa.deterministic import DeterministicTerm


class BrokenTimeTrend(DeterministicTerm):
    def __init__(self, break_period: int):
        self._break_period = break_period

    def __str__(self):
        return "Broken Time Trend"

    def _eq_attr(self):
        return (self._break_period,)

    def in_sample(self, index: pd.Index):
        nobs = index.shape[0]
        terms = np.zeros((nobs, 2))
        terms[self._break_period :, 0] = 1
        terms[self._break_period :, 1] = np.arange(
            self._break_period + 1, nobs + 1
        )
        return pd.DataFrame(
            terms, columns=["const_break", "trend_break"], index=index
        )

    def out_of_sample(
        self, steps: int, index: pd.Index, forecast_index: pd.Index = None
    ):
        # Always call extend index first
        fcast_index = self._extend_index(index, steps, forecast_index)
        nobs = index.shape[0]
        terms = np.zeros((steps, 2))
        # Assume break period is in-sample
        terms[:, 0] = 1
        terms[:, 1] = np.arange(nobs + 1, nobs + steps + 1)
        return pd.DataFrame(
            terms, columns=["const_break", "trend_break"], index=fcast_index
        )

btt = BrokenTimeTrend(60)
tt = TimeTrend(constant=True, order=1)
index = pd.RangeIndex(100)
det_proc = DeterministicProcess(index, additional_terms=[tt, btt])
det_proc.range(55, 65)
#
const	trend	const_break	trend_break
55	1.0	56.0	0.0	0.0
56	1.0	57.0	0.0	0.0
57	1.0	58.0	0.0	0.0
58	1.0	59.0	0.0	0.0
59	1.0	60.0	0.0	0.0
60	1.0	61.0	1.0	61.0
61	1.0	62.0	1.0	62.0
62	1.0	63.0	1.0	63.0
63	1.0	64.0	1.0	64.0
64	1.0	65.0	1.0	65.0
65	1.0	66.0	1.0	66.0

次に、実際の外生的データのシンプルな「ラッパー」を書くことで、サンプル外の外生データを簡単に構築し、予測のために利用します。

class ExogenousProcess(DeterministicTerm):
    def __init__(self, data):
        self._data = data

    def __str__(self):
        return "Custom Exog Process"

    def _eq_attr(self):
        return (id(self._data),)

    def in_sample(self, index: pd.Index):
        return self._data.loc[index]

    def out_of_sample(
        self, steps: int, index: pd.Index, forecast_index: pd.Index = None
    ):
        forecast_index = self._extend_index(index, steps, forecast_index)
        return self._data.loc[forecast_index]

import numpy as np

gen = np.random.default_rng(98765432101234567890)
exog = pd.DataFrame(
    gen.integers(100, size=(300, 2)), columns=["exog1", "exog2"]
)
exog.head()
#
exog1	exog2
0	6	99
1	64	28
2	15	81
3	54	8
4	12	8

DeterministicProcessをサポートするモデル

DeterministicProcessを直接サポートしているモデルはAutoRegだけです。カスタムな項は、決定論的キーワード引数を使用して設定することができます。

注意: カスタムな項を使用するには、 trend="n "とseasonal=Falseが必要なので、すべての決定論的要素はカスタム決定論的項から来ていなければなりません。

いくつかのデータのシミュレーション

ここでは、フーリエ級数によって捕捉された週ごとの季節性を持つデータをシミュレーションしています。

gen = np.random.default_rng(98765432101234567890)
idx = pd.RangeIndex(200)
det_proc = DeterministicProcess(idx, constant=True, period=52, fourier=2)
det_terms = det_proc.in_sample().to_numpy()
params = np.array([1.0, 3, -1, 4, -2])
exog = det_terms @ params
y = np.empty(200)
y[0] = det_terms[0] @ params + gen.standard_normal()
for i in range(1, 200):
    y[i] = 0.9 * y[i - 1] + det_terms[i] @ params + gen.standard_normal()
y = pd.Series(y, index=idx)
ax = y.plot()

seasonalのデフォルトはFalseですが、deterministicのデフォルトは "c "なので、これを変更する必要があります。

from statsmodels.tsa.api import AutoReg

mod = AutoReg(y, 1, trend="n", deterministic=det_proc)
res = mod.fit()
print(res.summary())
#
AutoReg Model Results                             
==============================================================================
Dep. Variable:                      y   No. Observations:                  200
Model:                     AutoReg(1)   Log Likelihood                -270.964
Method:               Conditional MLE   S.D. of innovations              0.944
Date:                Tue, 23 Feb 2021   AIC                             -0.044
Time:                        13:06:33   BIC                              0.072
Sample:                             1   HQIC                             0.003
                                  200                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
const          0.8436      0.172      4.916      0.000       0.507       1.180
sin(1,52)      2.9738      0.160     18.587      0.000       2.660       3.287
cos(1,52)     -0.6771      0.284     -2.380      0.017      -1.235      -0.120
sin(2,52)      3.9951      0.099     40.336      0.000       3.801       4.189
cos(2,52)     -1.7206      0.264     -6.519      0.000      -2.238      -1.203
y.L1           0.9116      0.014     63.264      0.000       0.883       0.940
                                    Roots                                    
=============================================================================
                  Real          Imaginary           Modulus         Frequency
-----------------------------------------------------------------------------
AR.1            1.0970           +0.0000j            1.0970            0.0000
-----------------------------------------------------------------------------

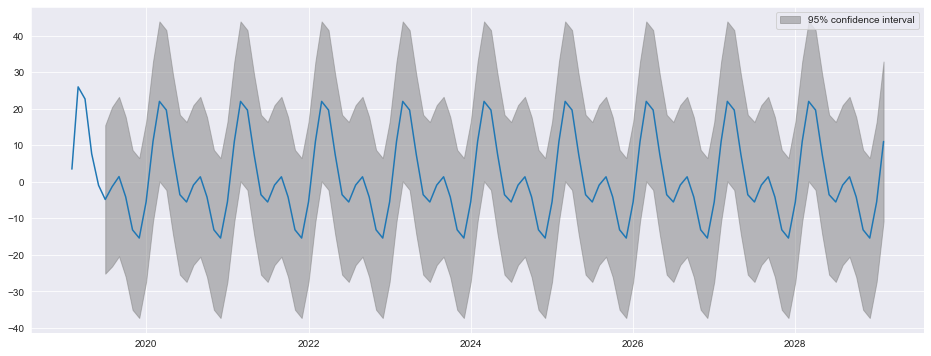
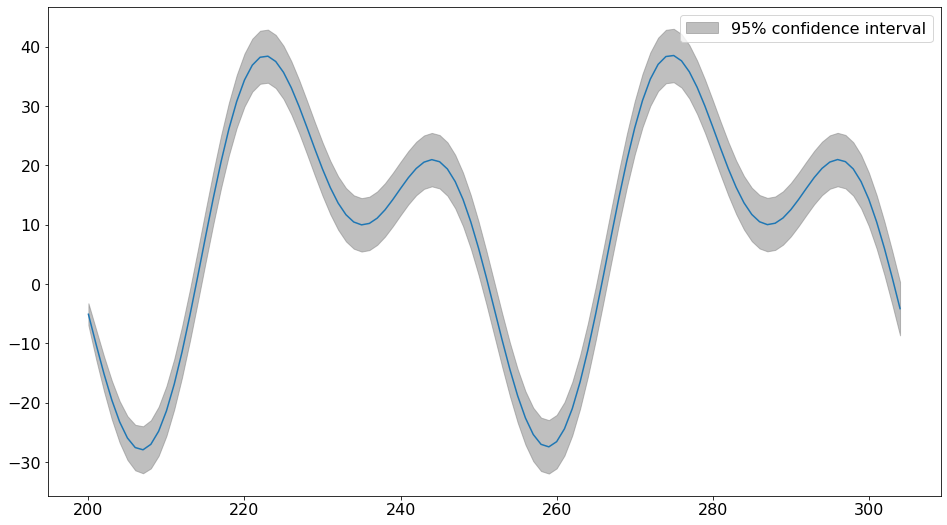
plot_predictを使用して、予測値とその予測間隔を表示することができます。サンプル外の決定論的な値は、AutoRegに渡された決定論的な処理によって自動的に生成されます。

fig = res.plot_predict(200, 200 + 2 * 52, True)

auto_reg_forecast = res.predict(200, 211)
auto_reg_forecast
#
200    -3.253482
201    -8.555660
202   -13.607557
203   -18.152622
204   -21.950370
205   -24.790116
206   -26.503171
207   -26.972781
208   -26.141244
209   -24.013773
210   -20.658891
211   -16.205310
dtype: float64

from statsmodels.tsa.api import SARIMAX

det_proc = DeterministicProcess(idx, period=52, fourier=2)
det_terms = det_proc.in_sample()
#
200    -3.253482
201    -8.555660
202   -13.607557
203   -18.152622
204   -21.950370
205   -24.790116
206   -26.503171
207   -26.972781
208   -26.141244
209   -24.013773
210   -20.658891
211   -16.205310
dtype: float64

他のモデルとの併用

他のモデルは、DeterministicProcessを直接サポートしていません。代わりに、外生変数をサポートするモデルに、任意の決定論的項をexogとして手渡すことができます。

外生変数を含むSARIMAXは、SARIMAエラーを含むOLSであることに注意してください。

決定論的項のパラメータは、式に従って進化する AutoReg と直接比較することはできません。

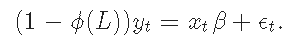
xt が決定論的項のみを含む場合、これら 2 つの表現は等価である (MA が存在しないように θ(L)=0 と仮定する)。

mod = SARIMAX(y, order=(1, 0, 0), trend="c", exog=det_terms)
res = mod.fit(disp=False)
print(res.summary())
#
 SARIMAX Results                                
==============================================================================
Dep. Variable:                      y   No. Observations:                  200
Model:               SARIMAX(1, 0, 0)   Log Likelihood                -293.381
Date:                Tue, 23 Feb 2021   AIC                            600.763
Time:                        13:07:33   BIC                            623.851
Sample:                             0   HQIC                           610.106
                                - 200                                         
Covariance Type:                  opg                                         
==============================================================================
                 coef    std err          z      P>|z|      [0.025      0.975]
------------------------------------------------------------------------------
intercept      0.0796      0.140      0.567      0.570      -0.196       0.355
sin(1,52)      9.1916      0.876     10.492      0.000       7.475      10.909
cos(1,52)    -17.4348      0.891    -19.576      0.000     -19.180     -15.689
sin(2,52)      1.2512      0.466      2.683      0.007       0.337       2.165
cos(2,52)    -17.1863      0.434    -39.583      0.000     -18.037     -16.335
ar.L1          0.9957      0.007    150.762      0.000       0.983       1.009
sigma2         1.0748      0.119      9.068      0.000       0.842       1.307
===================================================================================
Ljung-Box (L1) (Q):                   2.16   Jarque-Bera (JB):                 1.03
Prob(Q):                              0.14   Prob(JB):                         0.60
Heteroskedasticity (H):               0.71   Skew:                            -0.14
Prob(H) (two-sided):                  0.16   Kurtosis:                         2.78
===================================================================================

Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

予測は似ていますが、SARIMAXのパラメータがMLEを用いて推定されているのに対し、AutoRegはOLSを用いて推定されている点が異なります。

sarimax_forecast = res.forecast(12, exog=det_proc.out_of_sample(12))
df = pd.concat([auto_reg_forecast, sarimax_forecast], axis=1)
df.columns = columns = ["AutoReg", "SARIMAX"]
df
#
AutoReg	SARIMAX
200	-3.253482	-2.956562
201	-8.555660	-7.985589
202	-13.607557	-12.794073
203	-18.152622	-17.130964
204	-21.950370	-20.760474
205	-24.790116	-23.475512
206	-26.503171	-25.109630
207	-26.972781	-25.546790
208	-26.141244	-24.728386
209	-24.013773	-22.657095
210	-20.658891	-19.397353
211	-16.205310	-15.072386

Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。