Python3ではじめるシステムトレード：長期投資

本記事のjupyter notebook ファイル(yahoo_finance_LT.ipynb)はhttps://github.com/innovation1005/system_trade
からダウンロード可能です。

長期投資の基本

本記事では最も基本的なデータ分析の方法を長期投資を念頭に学びます。

• 手に入る長期間のデータで値動きの特徴を分析
• 市場規模の把握
• 見せかけのトレンドとランダムウォーク
• 破綻をさけるために

手に入る長期間のデータで値動きの特徴を分析

直近のそれなりのデータを使った方が、適切な分析ができるのではと思っていませんか？株式市場は生き物のようなもので、性質がちょくちょく変わるので短いデータで分析するべきだという話を時たま耳にします。しかし、それは間違いです。短いデータで分析をすると、自分が期待している結果がすぐに出るのだと誤解をしてしまいます。過去を分析するということは、自分の期待を裏切らない結果を選択するということになってしまいがちです。分析に使うデータは長いに越したことはありません。長すぎるということはありません。その方が、自分が期待する結果は出にくくなるのです。事実と対面することができるのです。時にはモンテカルロ法で疑似的にデータを作る必要もあるほどですから。

市場規模の把握

長期投資の基本は相手をよく知ること。それは他と比べることから始まります。投資をする際にはまずは正確にその市場規模を理解しておくことが重要です。

日本の株式市場の時価総額	USD 6.7 T	2020 wiki
米国の株式市場の時価総額	USD 44 T	2020 wiki
NY証券取引所の時価総額	USD 22 T	2023/1 wiki
米国ナスダックの時価総額	USD 18 T	2023/1 wiki
SP500 株価指数の時価総額	USD 33 T	2022/12 wiki
世界の株式市場の時価総額	USD 94 T	2020 wiki
米国債市場	USD 23 T	2022/6 wiki
日本の国債市場	USD 9.8 T	2022/12 wiki

SPY時価総額	USD 0.38T	yahoo finance 2023/5/26
アジアの株式ETF	USD 0.9T	wiki
米国の株式ETF	USD 5.4 T	wiki
米国の債券ETF	USD 1.4 T	wiki
米国のMutual Fund運用資産残高	USD 23.9T	2020/12 wiki
日本のMutual Fund運用資産残高	USD 2.1T	2020/12 wiki
ヘッジファンドの運用資産残高	USD 3.8 T	2021 wiki

大体の規模感がつかめたのではないでしょうか？少なくとも米国の金融市場は日本よりもバカでかい。かつ日本の国債市場は株式市場よりも大きい。しかし、米国の場合にはそうではありません。国民一人当たりのGDPが両国で同じであるとすると、どちらの株式市場が上昇しやすいでしょうか？日本の場合には多くの新しく生産されたサービスや付加価値の対価が金利の支払いに回されています。

他人のお金で経済活動をする

ここでの 債務 の意味は、特定の主体（政府、民間部門、または金融部門）が借り入れた資金を返済する義務を指します。それぞれのセクターごとに債務の性質が異なりますが、一般的には以下のように定義されます：

公的債務

意味 : 政府が発行する債券やその他の借り入れに基づく債務。通常、財政赤字の補填や公共事業の資金調達のために行われます。

• 内訳 : 国内債務（国民や国内金融機関からの借り入れ）と外債（外国からの借り入れ）。
• 返済元 : 将来の税収や財政収入。

民間部門の債務（Private Sector Debt）

意味 : 家計や非金融企業が銀行、金融市場、または他の貸し手から借り入れた負債。

• 家計債務 :

• 住宅ローン、クレジットカードローン、自動車ローンなどが含まれる。

• 消費者が日常生活や資産購入のために利用する資金。

• 非金融企業の債務 :

• 企業が設備投資や運転資金のために借り入れた資金。

• 社債や銀行融資が主要な形態。

金融部門の債務（Financial Sector Debt）

意味 : 銀行、保険会社、投資会社などの金融機関が他の金融機関や市場から調達した資金。

• 性質 : 主に短期のインターバンク借入、レポ取引、または金融機関が顧客資金を使って調達する形式。
• 役割 : 金融市場の流動性維持や仲介機能を支える。

株式時価総額との違い

• 債務は「返済義務のある資金調達」である一方、株式は「返済義務のない資本調達」。
• 株式の発行で得た資金は、出資者が企業の所有権を持つ代わりに返済不要。

主な国際的な資金調達手段：債務と資本

各国の公的債務、民間部門および金融部門の債務残高、ならびに株式時価総額について、以下に国別の概要を示します。

１． アメリカ合衆国

• 公的債務 : 2021年時点で、アメリカの連邦政府債務は約28兆ドルに達し、GDP比で約125%となっています。

• 民間部門の債務 : 非金融企業および家計の債務合計は約32兆ドルで、GDP比で約140%です。

• 金融部門の債務 : 金融機関の債務は約20兆ドルで、GDP比で約90%です。

• 株式時価総額 : 2024年10月末時点で、アメリカの株式時価総額は約60.8兆ドルで、世界全体の約49.1%を占めています。

２．ユーロ圏

• 公的債務 : ユーロ圏全体の政府債務は約12兆ユーロで、GDP比で約98%です。

• 民間部門の債務 : 非金融企業および家計の債務合計は約14兆ユーロで、GDP比で約115%です。

• 金融部門の債務 : 金融機関の債務は約10兆ユーロで、GDP比で約82%です。

• 株式時価総額 : ユーロ圏の株式時価総額は約8兆ユーロで、世界全体の約10%を占めています。

３． 日本

• 公的債務 : 2021年時点で、日本の政府債務は約1,200兆円で、GDP比で約240%に達しています。

• 民間部門の債務 : 非金融企業および家計の債務合計は約900兆円で、GDP比で約180%です。

• 金融部門の債務 : 金融機関の債務は約600兆円で、GDP比で約120%です。

• 株式時価総額 : 2024年10月末時点で、日本の株式時価総額は約6.4兆ドルで、世界全体の約5.2%を占めています。

４． 中国

• 公的債務 : 中国の政府債務は約45兆元で、GDP比で約70%です。

• 民間部門の債務 : 非金融企業および家計の債務合計は約160兆元で、GDP比で約250%です。

• 金融部門の債務 : 金融機関の債務は約100兆元で、GDP比で約150%です。

• 株式時価総額 : 2024年10月末時点で、中国の株式時価総額は約10.2兆ドルで、世界全体の約8.3%を占めています。

前提条件

GDP比率：政府債務、民間債務、金融機関の債務、および株式時価総額はすべてGDPに対する比率で表されます。
静的な視点：現在の状態のみを分析し、過去や将来の変動要因は考慮しません。

静的な視点において、政府債務、民間債務、金融機関の債務がGDP比で高い場合、これらの債務に関連する資金の配分が株式市場への資金供給を制約し、株式時価総額が抑制される傾向があります。逆に、債務比率が低い場合は、株式市場への資金流入が促進され、株式時価総額が増加する可能性があります。

しかし、この関係は単純な逆相関ではなく、他の経済指標や市場要因も同時に影響を与えるため、債務比率と株式時価総額の関係を評価する際には、これらの要素も考慮する必要があります。例えば、産業構造や市場の成熟度、規制環境などが関与することで、債務比率と株式時価総額の関係性に変動が生じることがあります。

したがって、現時点での債務比率と株式時価総額の関係を理解するためには、これらの要素を総合的に考慮することが重要です。

見せかけのトレンドとランダムウォーク

多くの経済時系列や株価はランダムウォークにしたがいます。ランダムウォークにしたがう時系列は時間の経過にともない平均や分散が変化してしまいます。ランダムウォークでは時間の経過とともに平均は確率的に変化し、分散は時間の経過の平方根に比例して増大します。したがって、その株価の将来は予測が不可能です。予測ができないということは売買するタイミングを図っても意味がありません。ランダムウォークが酔っ払いの千鳥足にたとえられるように将来どこに行くの分からないのです。かつ時間の経過とともにその幅は大きくなります。つまり、大きく上昇するかもしれませんが、下落もします。

株価データがランダムウォークにしたがうかどうかを知ることはつぎの2つの点から重要です。

1. 発生したトレンドが見せかけのトレンドか、トレンドはたまたま生じたものなのか、
2. ２つの時系列が相関を示したときにそれらは見せかけの相関か、たまたま発生したものではないのか、

という点です。ランダムウォークでは簡単にトレンドが発生します。それを見せかけのトレンドといいます。そして、そういうトレンドに対して相関を取ると、見せかけの相関が現れます。このような疑似的な統計的性質は役に立ちません。つまり、見せかけでないことを明確にする情報があったり、そうなる理由が明確で真のトレンドがあるのだという確信があるとき以外は投資できません。

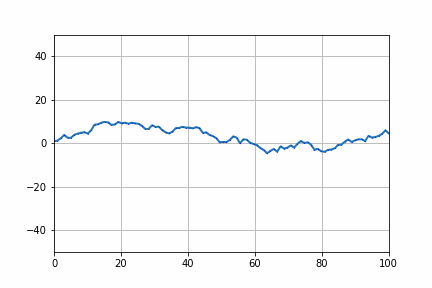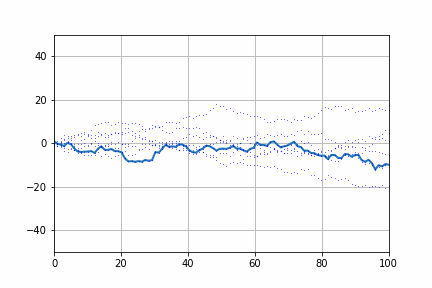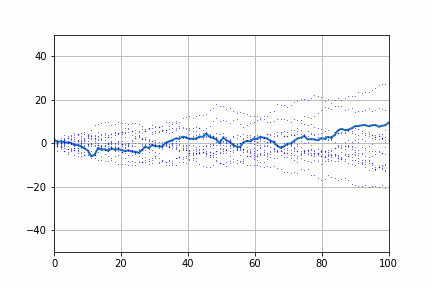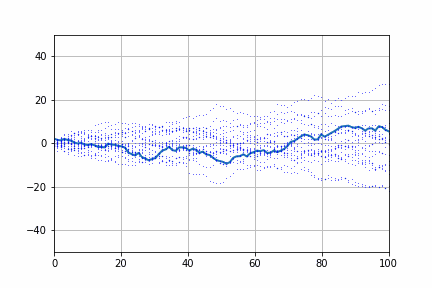
Pythonでランダムウォークをつくってみましょう。つぎの図は乱数が作った株価の動きです。様々な動きをしますが、上昇トレンドや下落トレンドを作ることがあります。大体20回に一度そのような相場が現れます。これは株価がランダムに動いたとしてもトレンドが発生することを示しています。

%matplotlib inline 
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as ss
from matplotlib.animation import FuncAnimation
import pandas_datareader.data as web #データのダウンロードライブラリ

fig, ax = plt.subplots()
ax.set_xlim(0, 100)
ax.set_ylim(-50, 50)
ax.grid(True)
line, = ax.plot([], [],linestyle='-', linewidth=2)     
locus, = ax.plot([], [], 'b.', linewidth=1,markersize=0.5)     
def animate(i):
    x = np.linspace(0, 100,100)
    y = np.cumsum(np.random.randn(100,))
    line.set_data(x, y)
    xlocus.append(x)
    ylocus.append(y)
    locus.set_data(xlocus, ylocus)
    return line,
xlocus, ylocus = [], []
anim = FuncAnimation(fig, animate, frames=np.arange(20), 
                     interval=1000, blit=False,repeat=False)
anim.save('randomwalk.gif', writer="pillow")
plt.show()

つぎに実際の株価を見てみましょう。株価がランダムウォークであるかどうかを判定する方法としてディッキーフラー検定があります。statsmodelsでは４つのタイプの検定を用意しています。

• ドリフト無しランダムウォーク(rw)
• ドリフト付きランダムウォーク(drw)
• 時間トレンド・ドリフト付きランダムショーク(tdrw)
• 加速度付き時間トレンド・ドリフト付きランダムウォーク(qtdrw)

これらの結果が0.1以下であれば、ランダムウォークでない可能性が高まります。

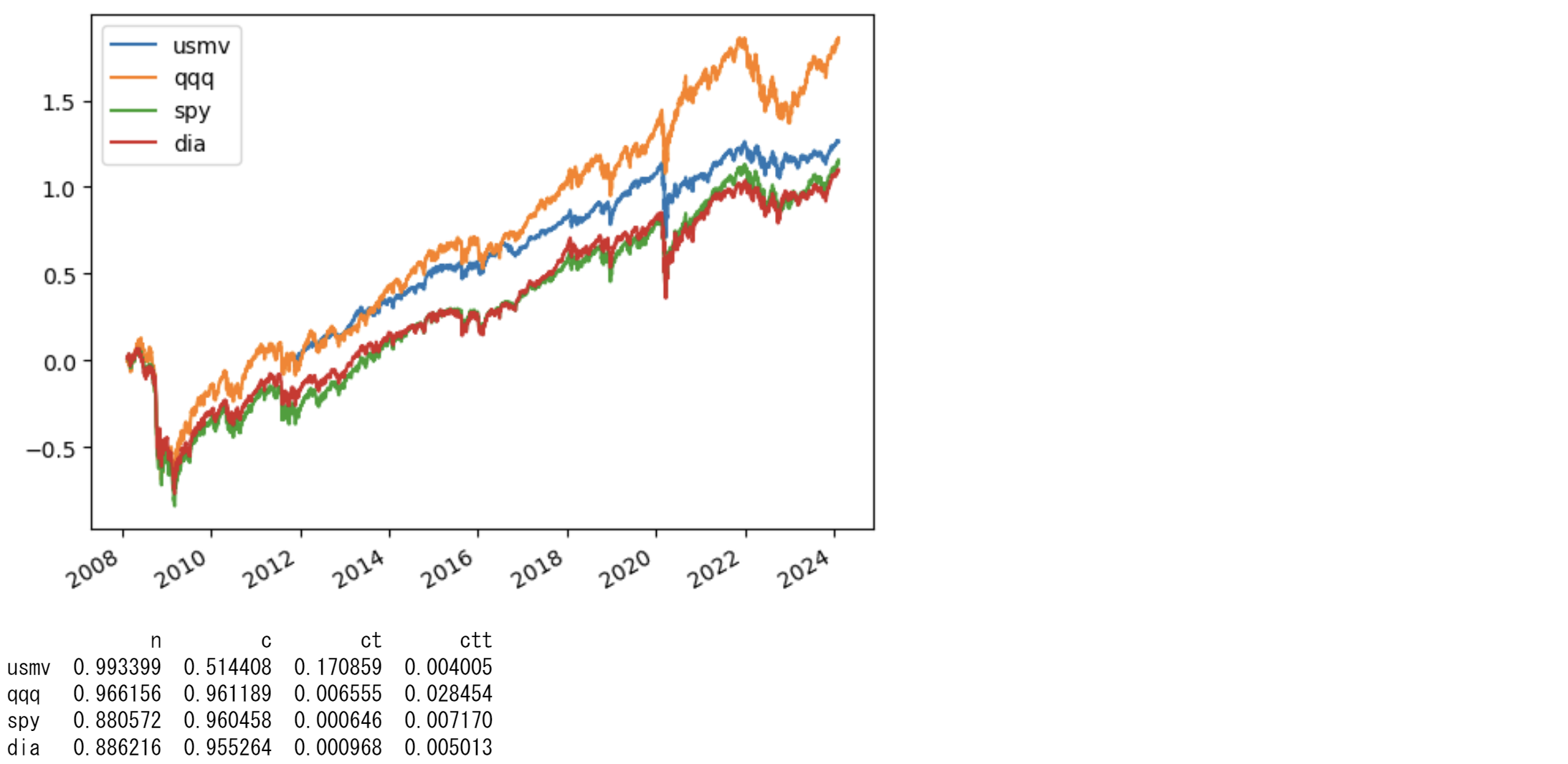
実際に、最小分散ポートフォリオ(usmv),ナスダック１００(qqq),S&P500(spy),ダウ平均(dia)についてみてみましょう。

from statsmodels.tsa.stattools import adfuller

BASIC=['usmv','qqq','spy','dia']

ror = web.DataReader("DGS1","fred","1980/1/4")#米国連邦準備委員会のホームページから米国金利をダウンロード
ror = ror/250/100#jpy

def LongtermInvest(PORT,ror):
    i=1
    adf=[]
    assets=[]
    for asset in PORT:
        tsd = yf.Ticker(asset).history(period="16y")
        dtsd=np.log(tsd.Close).diff().dropna()
        da=dtsd.index.date
        da=pd.to_datetime(da)
        dtsd=pd.DataFrame(dtsd.values,index=da)
        dtsd.columns=['Close']

        tmp=pd.concat([dtsd,ror],axis=1).dropna()
        tmp['adj']=(1+tmp.iloc[:,0]/(1+tmp.iloc[:,1]))
        tsda=tmp.iloc[:,2].cumprod()
        ts=np.log(tsda.dropna())
        ts.plot(label=str(asset))
        assets.append(asset)
        adf.append([adfuller((ts),regression='n')[1],
            adfuller((ts),regression='c')[1],
            adfuller((ts),regression='ct')[1],
            adfuller((ts),regression='ctt')[1]])
        if i==5:
            plt.legend()
            plt.show()
            i=0
        i+=1
    if i!=1:
        plt.legend()
        plt.show()    
    db=pd.DataFrame(adf,index=assets,columns=['n','c','ct','ctt'])
    print(db)
i=1
LongtermInvest(BASIC,ror)

結果は順に、ドリフト無しランダムウォーク(n)、ドリフト付きランダムウォーク(c)、時間トレンド・ドリフト付きランダムショーク(ct)、加速度付き時間トレンド・ドリフト付きランダムウォーク(ctt)です。usmvでは'ctt',qqqでは'ct'と'ctt'で,spyでは'ct'、'ctt'で,diaでは'ct'と'ctt'において単位根の帰無仮説を棄却しています。これらの検定では単位根であるなしの検定しかできませんが、ランダムウォークの有無の判定に使われます。この結果からはランダムウォークであるとは言い切れない程度のことしか統計学的には分かりません。つまり、短い期間のタイミングを見た売買で利益を上げるのは難しいのですが、時間を掛ければ投資する意義はありそうだということぐらいは分かります。
​

破綻を避けるために

4つの基本株式売買戦略のうち破綻する確率が低いのはどれでしょうか？

• リバランス：価格が動いたことにより、投資比率が目標値からずれたら元に戻す戦略
• 損切り：損が出たら、ポジションを閉じる
• オプション：保険のようにプレミアムを払ってリスクを回避
• 買い持ち(バイアンドホルド)：買いポジションを保有し続ける

この中で破綻する確率が低い戦略はリバランスと買い持ちだけです。

オプションはオプション料に見合う収益が得られなれば破綻します。

損切は、その損が収益よりも大きければ破綻します。

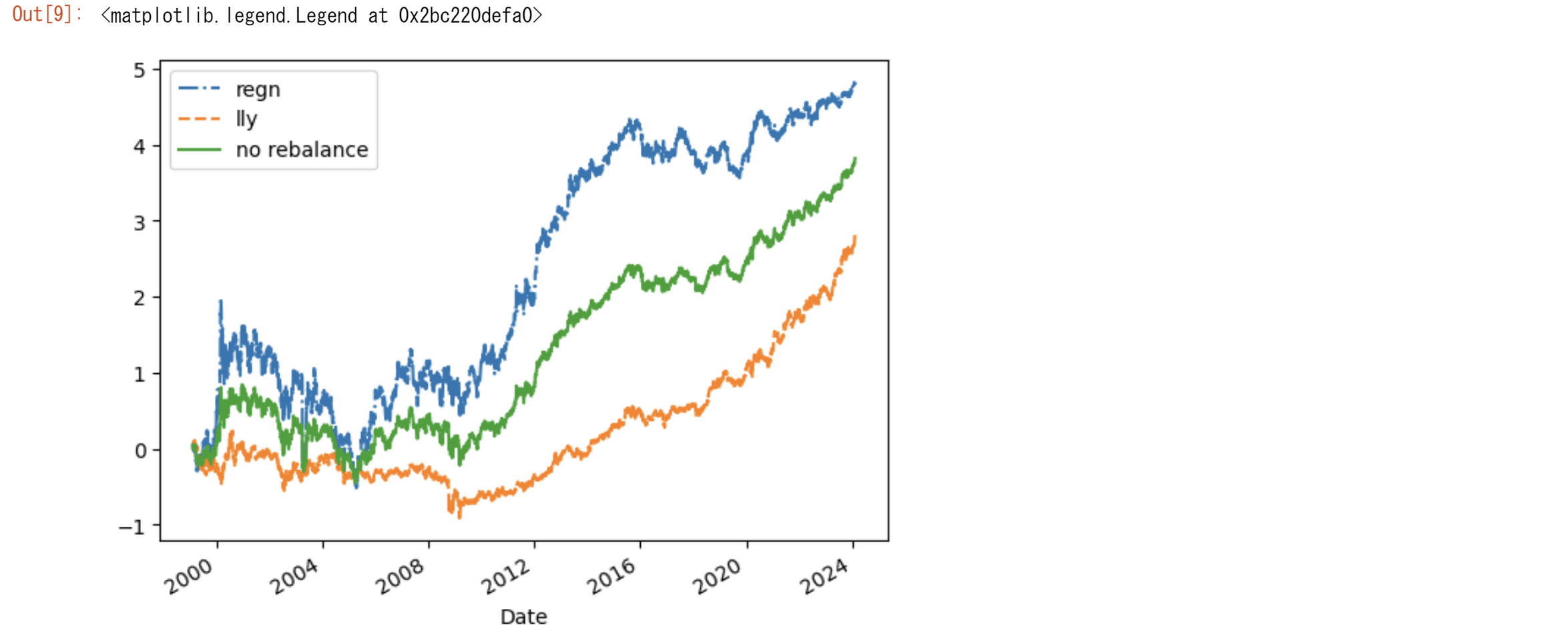
2つの銘柄をつかってシミュレーションをしてみましょう。つぎのプログラムは最初に半々で投資した後にポジションを動かさないでいた場合のシミュレーションです。この場合には投資の価値の比率は株価が上がったほうの株が高くなります。

ticker1="regn"
ticker2="lly"
asset1=yf.Ticker(ticker1).history(period="25y")
asset2=yf.Ticker(ticker2).history(period="25y")
asset1=asset1.Close.loc['1998/5/26':]
asset2=asset2.Close.loc['1998/5/26':]

asset1=asset1/asset1.iloc[0]#株価の指数化
lnasset1=np.log(asset1)
dlasset1=lnasset1.diff().dropna()
asset2=asset2/asset2.iloc[0]
lnasset2=np.log(asset2)
dlnasset2=lnasset2.diff().dropna()
lnasset1.plot(label=ticker1,style='-.')
lnasset2.plot(label=ticker2,linestyle='--')
lnport=0.5*lnasset1+0.5*lnasset2
lnport.plot(label='no rebalance')
plt.legend(loc='upper left')

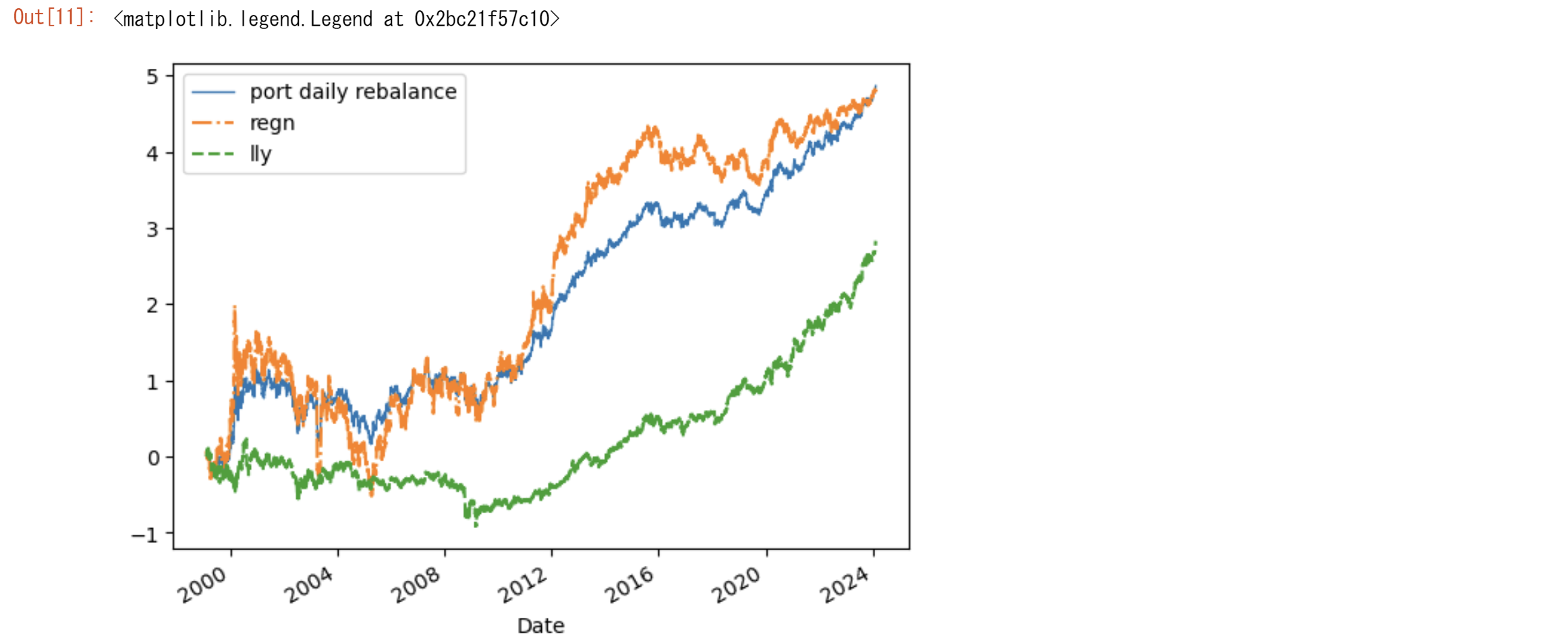
つぎのシミュレーションは毎日リバランスを行って、つねに投資の価値が50％50％の比率になるように調整するプログラムです。

def portfolio_rebalance(tsd1,tsd2):
    port=pd.concat([tsd1,tsd2],axis=1).dropna()
    port.columns=('p1','p2')
    port['a1']=0
    port['a2']=0
    port['v']=1
    n=len(port)
    p1=port['p1'].iloc[0]
    p2=port['p2'].iloc[0]
    v=port['v'].iloc[0]
    a1=float(v/2/p1)
    a2=float(v/2/p2)
    port.iloc[0,2]=a1
    port.iloc[0,3]=a2
    for i in range(1,len(port)):
        p1=port['p1'].iloc[i]#今日のasset1の株価
        p2=port['p2'].iloc[i]#今日のasset2の株価
        p1_0=port['p1'].iloc[i-1]#前日のasset1の株価
        p2_0=port['p2'].iloc[i-1]#前日のasset2の株価
        a1_0=port['a1'].iloc[i-1]#前日のasset1の保有株数
        a2_0=port['a2'].iloc[i-1]#前日のasset2の保有枚数
        v_0=port['v'].iloc[i-1]#前日のリバランスポートフォリオの価値
        #v=a1_0*(p1-p1_0)+a2_0*(p2-p2_0)+v_0#今日のリバランスポートフォリオの価値
        v=a1_0*p1+a2_0*p2#今日のリバランスポートフォリオの価値
        port.iloc[i,4]=v#リバランスポートフォリオの価値のアップデート
        a1=float(v/2/p1)#調整後のasset1の株数
        a2=float(v/2/p2)#調整後のasset2の株数
        port.iloc[i,2]=a1#asset1の株数のアップデート
        port.iloc[i,3]=a2#asset2の株数のアップデート
    port['v2']=0.5*port.p1+0.5*port.p2#リバランスの無いポートフォリオの価値
    return port

port=portfolio_rebalance(asset1,asset2)

lnport=np.log(port)
lnport.v.plot(label="port daily rebalance",linewidth=1.0)
lnasset1.plot(label=ticker1,style='-.')
lnasset2.plot(label=ticker2,linestyle='--')
plt.legend(loc="upper left")

リバランスの投資効率についてイメージがつかめたと思います。

さて、これで破綻を避けられますか？2銘柄の株を選んだとして、2つの会社が倒産してしまう確率はゼロではありません。株価指数に投資することでそのリスクを回避できます。初心者に株価指数への投資を進める理由はここにあります。

もうひとつ、ドルコスト平均法(積み立て投資)で破綻を避けることはできるでしょうか？破綻はさけられます。その投資効率は「買い持ち」戦略に近いものがあります。しかし、長い間、投資対象資産が下げ続けたらどうなるでしょうか？大きなこころのプレッシャーになると思いませんか？バブル崩壊後の日経平均、1990年代の金市場を考えてみてください。10年以上も続けて下げたならあなたはその資産に継続して投資できますか？それができるのであればドルコスト平均法は戦略の1つになります。

本記事そして本記事以外の分析の結果

• 株を購入したら利益が出るまで売らない
• 損切はしない
• 利益が出たらいつでも売っていいが、長く持った方が利益率は上がる

初心者は

• 分散投資された株価指数への投資を基本とするべきです

Pythonに不慣れな人に

Jupyter notebookのインストール
Yahoo Finance USから株価をダウンロードしてみた

ーーーーーーーーーーーーーーーーーーーーーーーー
Python3ではじめるシステムトレード【第2版】環境構築と売買戦略

「画像をクリックしていただくとpanrollingのホームページから書籍を購入していただけます。

Python3ではじめるシステムトレード改訂版　アマゾンから購入いただけます。

20240210090112610127167