タイトルそのままです.偏微分方程式をPythonで解きました.
問題
円柱座標系で,$z$軸に印加された磁場$B_z$中に静止した無限長の半径$a$,抵抗率$\eta$の円柱プラズマを考える.このプラズマに$z$軸方向の電流$I_z$を流す時,方位角方向の磁場$B_\theta$が発生する.プラズマに浸透する$B_\theta$と電流密度$J_z$の時空間発展を求める.
(金属に電流をいきなり流した時の過渡応答と同じになるっぽい.いわゆる表皮効果)
解きたい微分方程式
〜〜導出略〜〜
$$
\frac{\partial B_\theta}{\partial t} = \frac{\eta}{\mu_0}\frac{\partial}{\partial r}\left(\frac{1}{r} \frac{\partial (rB_\theta)}{\partial r}\right)
$$
$\mu_0$は真空の透磁率.また電流密度$J_z$は$\nabla \times B=\mu_0 J_z$より,
$$
J_z = \frac{1}{\mu_0r}\frac{\partial}{\partial r}(rB_\theta)
$$
$r>a$では$J_z=0$なので$B_\theta(r)=\mu_0I_z/2\pi r$.また,定常状態($\partial/\partial t=0$)で,左辺を解くと,$B_\theta(r)=(\mu_0I_z/2\pi a^2)r$になる($r=a$で$B_\theta(r)=\mu_0I_z/2\pi a$).$r$を$a$,$t$を$a^2\mu_0/\eta$,$B_\theta(r)$を$B_\theta(a)$,$J_\theta$を$I_z/\pi a^2$でそれぞれ規格化して整理すると,
\frac{\partial B_\theta}{\partial t} = \frac{\partial}{\partial r}\left(\frac{1}{r} \frac{\partial (rB_\theta)}{\partial r}\right)\\
= \left\{\frac{\partial^2}{\partial r^2} + \frac{1}{r} \frac{\partial}{\partial r} -\frac{1}{r^2} \right\}B_\theta
$$
J_z = \frac{1}{2}\frac{\partial}{\partial r}(rB_\theta)
$$
これを数値計算で解く.
離散化
以下,添字が煩雑なので$B_\theta$を$B$と書きます.時刻$t^j$,位置$r_i$における値を$B_i^j$,時間と距離の幅をそれぞれ$\Delta t$, $\Delta r$とする.
左辺について,
$$
(\text{左辺})=\frac{B_i^{j+1}-B_i^{j}}{\Delta t}
$$
右辺について
1階中心差分商と,
$$
\frac{\partial B}{\partial r} \approx \frac{B_{i+1}^j-B_{i+1}^j}{2\Delta r}
$$
2階中心差分商
$$
\frac{\partial B}{\partial r} \approx \frac{B_{i+1}^j-2B_{i}^j+B_{i-1}^j}{\Delta r^2}
$$
を使って書き下すと,
$$
(\text{右辺})=\frac{B_{i+1}^j-2B_{i}^j+B_{i-1}^j}{\Delta r^2}
+ \frac{1}{r_i}\frac{B_{i+1}^j
- B_{i+1}^j}{2\Delta r}-\frac{1}{r_i^2}B_i^j\
= \left(\frac{1}{\Delta r^2}-\frac{1}{2\Delta r}\right)B_{i-1}^j
- \left(-\frac{2}{\Delta r^2}+\frac{1}{r_i^2}\right)B_{i}^j
+ \left(\frac{1}{\Delta r^2}+\frac{1}{2\Delta r}\right)B_{i+1}^j\
=a_iB_{i-1}^j - b_iB_{i}^j + c_iB_{i+1}^j
$$
ここで$a_iB_{i-1}^j - b_iB_{i}^j + c_iB_{i+1}^j$を$\delta B_i^j$と定義する.
ここで,左辺と右辺の添字$j$の取り方で前進差分と後進差分がある.
前進差分
$j$を$\left(B_i^{j+1}-B_i^{j}\right)/\Delta t = \delta B_i^j$ととる方法で,時刻$j$の値から$j+1$を計算する(陽解法).$B_i^{j}$を移項すると漸化式になるので,計算が簡単.
しかし,$\Delta r$に対して$\Delta t$を細かくとらないと数値的に不安定になる.
後進差分
$j$を$\left(B_i^{j+1}-B_i^{j}\right)/\Delta t = \delta B_i^{j+1}$ととる方法.時刻$j$の値を満たすような$j+1$での値を計算する(陰解法).連立方程式を解く必要があり,ちょっとしんどい.
θ法
前進差分と後進差分のブレンド.
$$
\left(B_i^{j+1}-B_i^{j}\right)/\Delta t = (1-\theta)\delta B_i^j + \theta\delta B_i^{j+1}
$$
時間方向に2次精度になるらしい.参考
コード
差分方程式解く部分
import numpy as np
from tqdm import tqdm
def theta_method(n=10, m=100, theta=0.0, t_max=1.0):
n = int(n)
m = int(m)
r, h = np.linspace(0.0001, 1, n + 1, retstep=True)
t, tau = np.linspace(0, t_max, m + 1, retstep=True)
a = 1 / h ** 2 - 1 / (2 * r * h)
b = 2 / h ** 2 + 1 / r ** 2
c = 1 / h ** 2 + 1 / (2 * r * h)
B_theta = np.zeros((n + 1, m + 1))
w = np.zeros(n + 1)
A = np.zeros((n + 1, n + 1))
A[0, 0] = 1
A[n, n] = 1
for i in range(1, n):
A[i, i - 1] = -tau * theta * a[i]
A[i, i] = 1 + tau * theta * b[i]
A[i, i + 1] = -tau * theta * c[i]
B_theta[:, 0] = np.zeros_like(r)
for j in tqdm(range(m)):
w[0] = 0
w[n] = 1
w[1:n] = (1 - theta) * tau * a[1:n] * B_theta[:-2, j] \
+ (1 - (1 - theta) * tau * b[1:n]) * B_theta[1:n, j] \
+ (1 - theta) * tau * c[1:n] * B_theta[2:, j]
v = np.linalg.solve(A, w)
for i in range(n + 1):
B_theta[i, j + 1] = v[i]
return r, h, t, tau, B_theta, np.apply_along_axis(lambda B: calc_J_z(B, r), 0, B_theta)
def calc_J_z(B_theta, r):
return B_theta / r + np.gradient(B_theta, r)
描画
if __name__ == '__main__':
while True:
cmd = input("quit(q) or [enter]>>")
if cmd == "q":
break
else:
# t_list = np.array(list(map(float, input("t>>").split(","))))
t_list = np.array([0.0001, 0.001, 0.01, 0.1, 0.2, 0.5, 1])
n = int(input("n>>"))
m = int(input("m>>"))
theta = float(input("theta>>"))
cmd = input(f"lambda={n ** 2 * t_list.max() / m:.2} continue?(Y/n)>>")
if cmd == "n":
continue
r, h, t, tau, B_theta, J_z = theta_method(n=n, m=m, theta=theta, t_max=t_list.max())
ind = np.round(t_list / tau).astype(int)
B_theta_list = B_theta.T[ind]
J_z_list = J_z.T[ind]
B_theta_inf = r
J_z_inf = calc_J_z(r, r)
fig, axes = plt.subplots(1, 3, figsize=(12, 6), sharex=True)
fig.suptitle(rf"$n={n}$, $m={m}$, $\lambda={tau / h ** 2:.2}$, $\theta={theta:.2}$")
axes[0].set_title(r"$B_\theta$")
axes[0].set_ylabel(r"$B_\theta$")
axes[0].set_ylim(0.0, 1.1)
axes[1].set_title(r"$B_\theta$(steady)$-B_\theta$")
axes[1].set_ylabel(r"$B_\theta$")
axes[1].set_ylim(0.0, 1.1)
axes[2].set_title(r"$J_z$")
axes[2].set_ylabel(r"$J_z$")
axes[2].set_ylim(0., 5)
axes[0].set_xlim(0.0, 1.1)
axes[0].plot(r, B_theta_inf, ls="--", c="k", label="steady")
axes[1].plot(r, B_theta_inf, ls="--", c="k", label="steady")
axes[2].plot(r, J_z_inf, ls="--", c="k", label="steady")
for B, J, t_ in zip(B_theta_list, J_z_list, t_list):
axes[0].plot(r, B, label=f"t={t_:.2}")
axes[1].plot(r, B_theta_inf - B, label=f"t={t_:.2}")
axes[2].plot(r, J, label=f"t={t_:.2}")
for ax in axes:
ax.legend()
ax.set_xlabel(r"$r$")
ylim = ax.get_ylim()
ax.vlines(1, ylim[0], ylim[1], ls="-", colors="k", lw=1)
ax.set_ylim(0, ylim[1])
fig.tight_layout()
fig.savefig(f"B_theta_penetration_{n}_{m}_{theta}.png", bbox_inches="tight", pad_inches=0.05, dpi=200)
plt.show()
# animation
fig, axes = plt.subplots(1, 3, figsize=(12, 6), sharex=True)
# pick up 100 times from t_list in log scale
t_list_animation = np.unique(np.logspace(0, np.log10(m), MAX_FRAMES, dtype=int))
frame_number = len(t_list_animation)
skip = m // frame_number
def update(frame):
j = t_list_animation[frame]
axes[0].cla()
axes[1].cla()
axes[2].cla()
axes[0].set_title(rf"$B_\theta$ ($t={t[j]:.2}$)")
axes[0].set_ylabel(r"$B_\theta$")
axes[0].set_ylim(0.0, 1.1)
axes[1].set_title(rf"$B_\theta$(steady)$-B_\theta$ ($t={t[j]:.2}$)")
axes[1].set_ylabel(r"$B_\theta$")
axes[1].set_ylim(0.0, 1.1)
axes[2].set_title(rf"$J_z$ ($t={t[j]:.2}$)")
axes[2].set_ylabel(r"$J_z$")
axes[2].set_ylim(0., 5)
axes[0].plot(r, B_theta.T[j])
axes[1].plot(r, B_theta_inf - B_theta.T[j])
axes[2].plot(r, J_z.T[j])
axes[0].set_xlim(0.0, 1.1)
axes[0].plot(r, B_theta_inf, ls="--", c="k", label="steady")
axes[1].plot(r, B_theta_inf, ls="--", c="k", label="steady")
axes[2].plot(r, J_z_inf, ls="--", c="k", label="steady")
for ax in axes:
ax.legend()
ax.set_xlabel(r"$r$")
ylim = ax.get_ylim()
ax.vlines(1, ylim[0], ylim[1], ls="--", colors="k")
ax.set_ylim(0, ylim[1])
print("making animation...")
anim = FuncAnimation(fig, update, frames=range(frame_number), interval=200)
print("saving animation...")
anim.save(f"B_theta_penetration_{n}_{m}_{theta}.gif", writer="pillow", fps=10)
print("done.")
結果
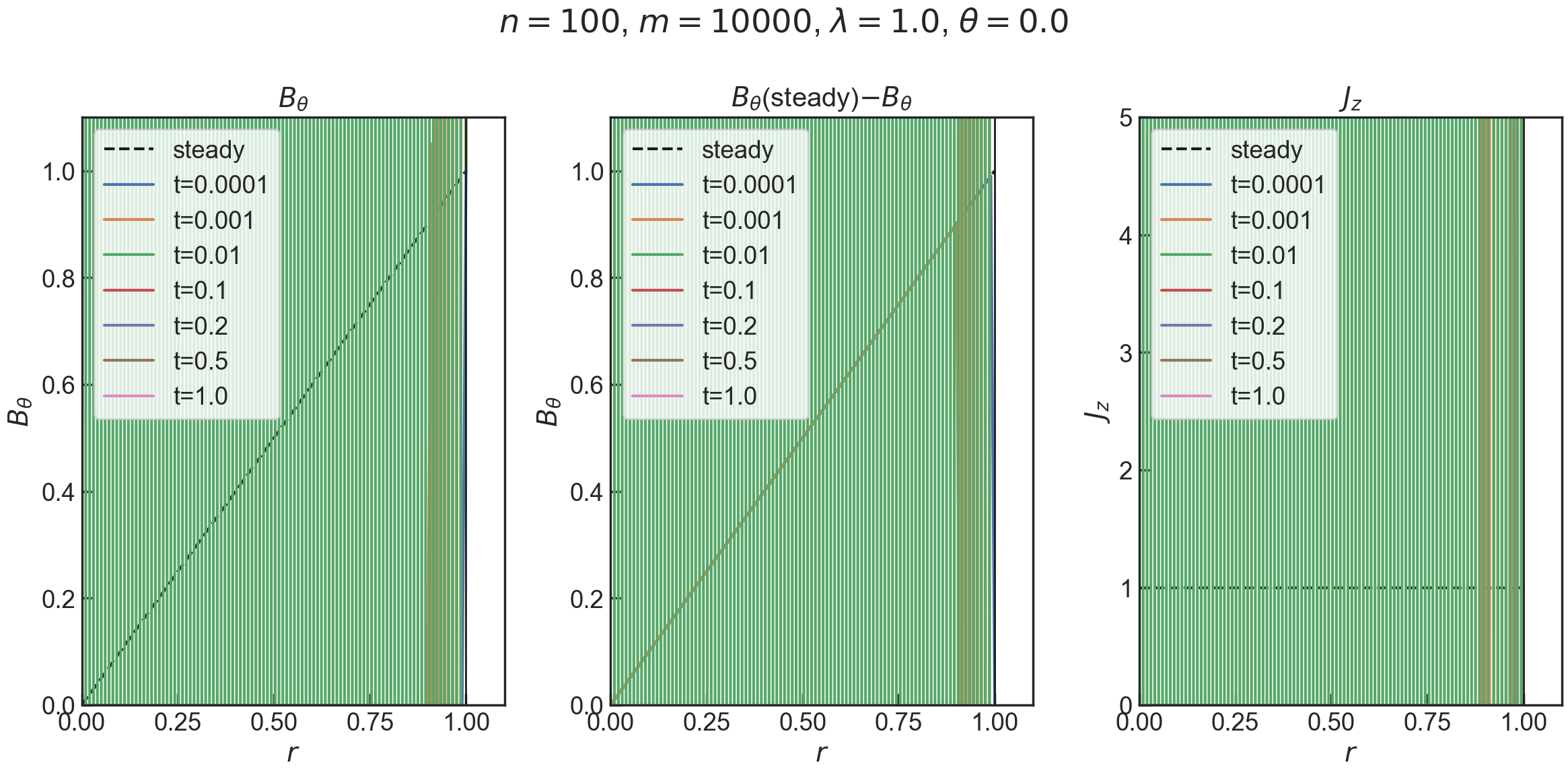
- $n=100$,$m=10000$,$\theta=0$(つまり前進差分)
解が不安定になっている.
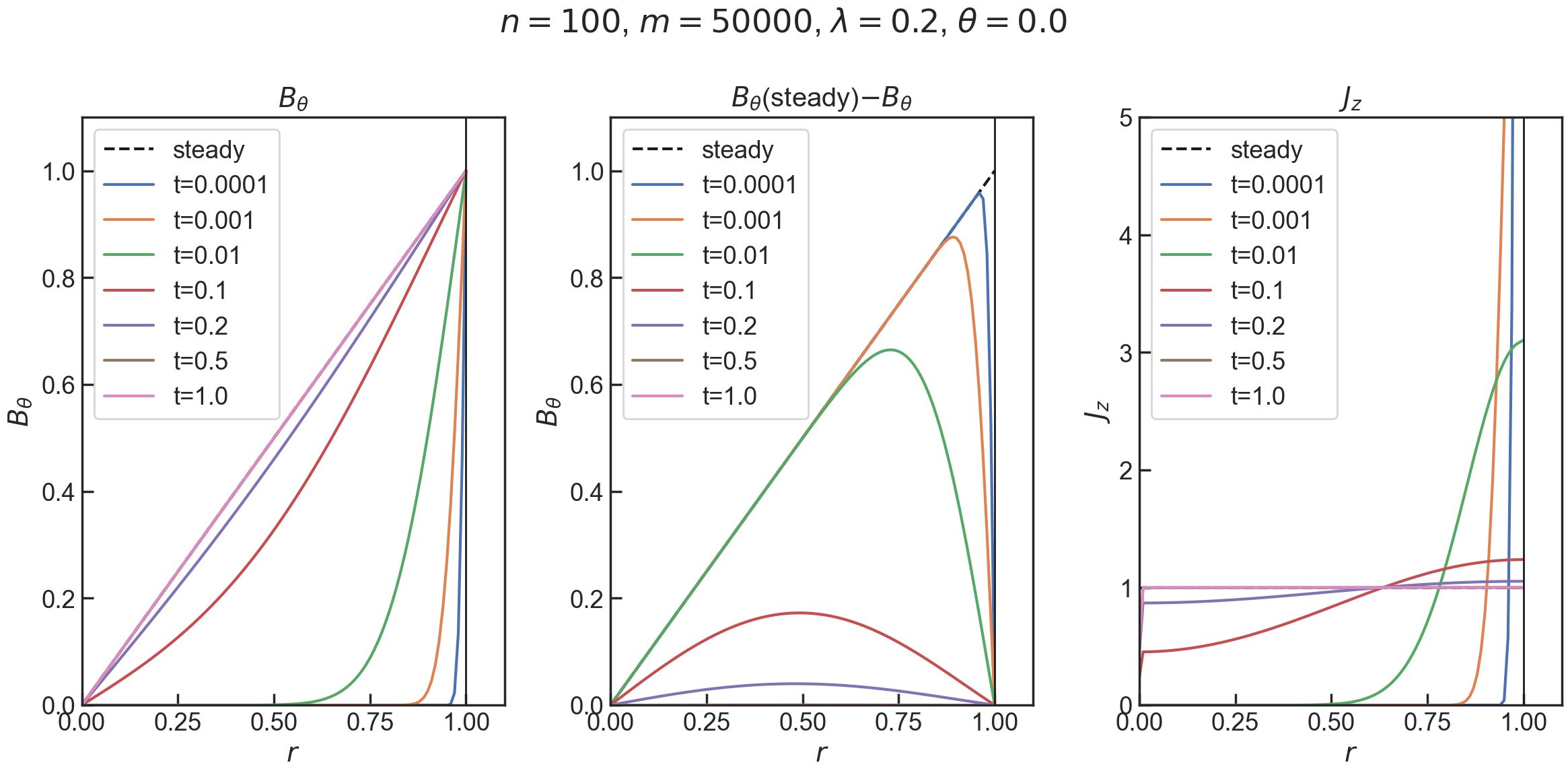
- $n=100$,$m=50000$,$\theta=0$(タイムステップを細かくした)
いい感じです.
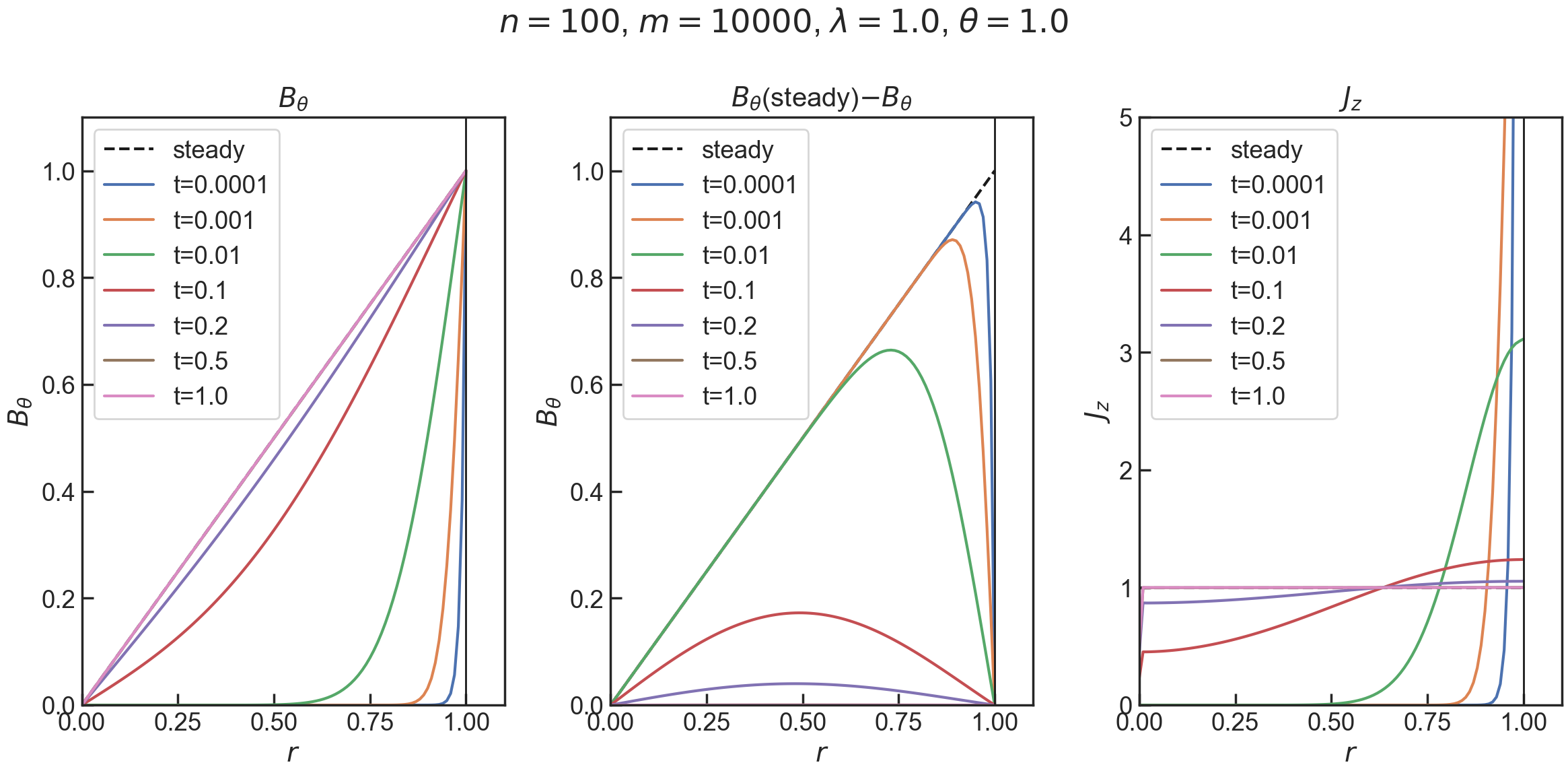
- $n=100$,$m=10000$,$\theta=1$(つまり後進差分)
前進差分では発散していたが,後進差分では安定している.
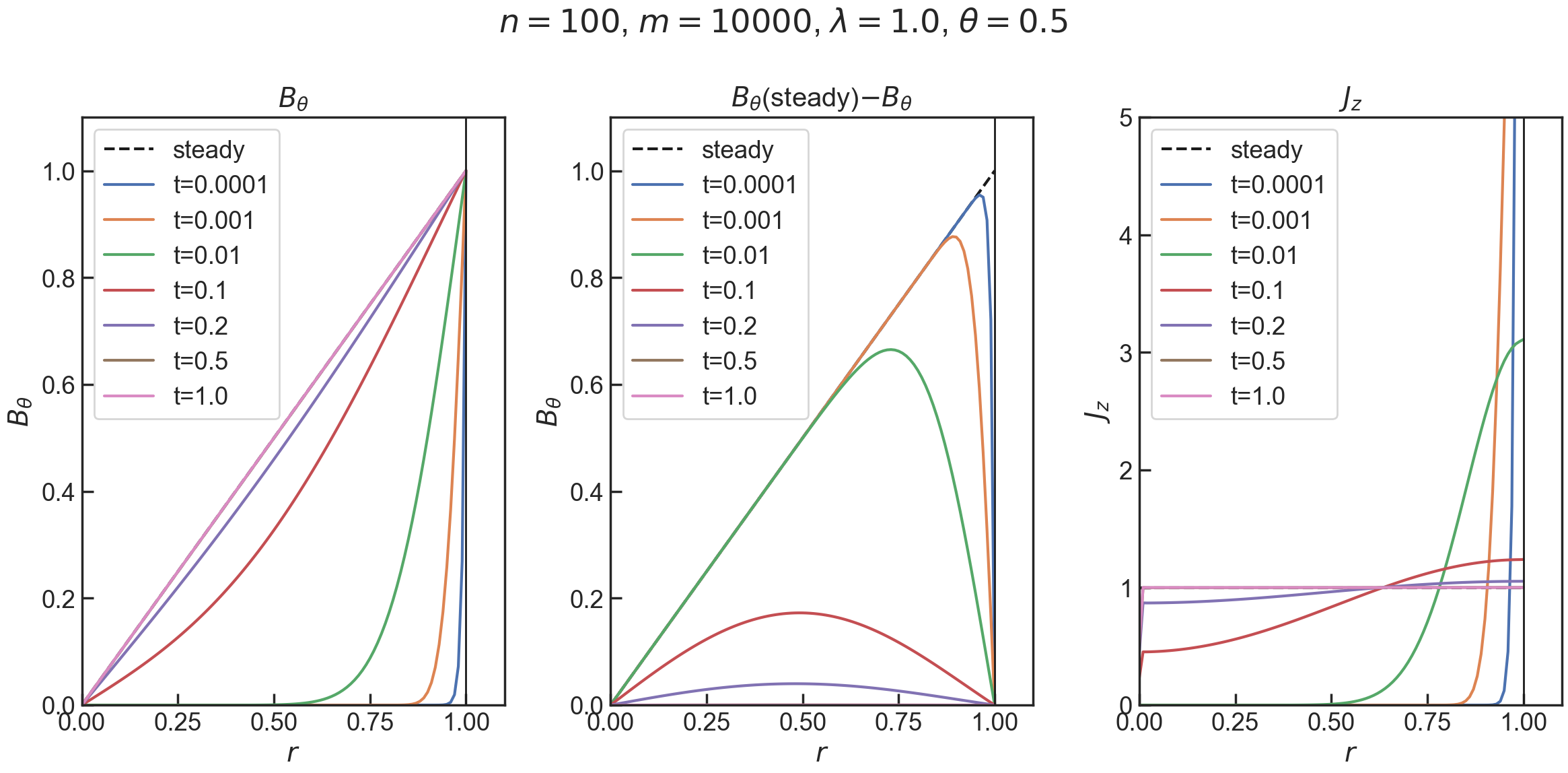
- $n=100$,$m=10000$,$\theta=0.5$
2, 3と同様の結果が得られた.精度はこれが一番いいらしい.
($t$に関する1次の誤差がキャンセルされるから?)