この記事は、先日の 2020年01月25日に慶応大学で開催されたシンポジウム「圏論的世界像からはじまる複合知の展望」の登壇資料を文字起こししたものです。
- Slide: 圏論とプログラミング / Category Theory and Programming - Speaker Deck
- Video: 圏論とプログラミング / 稲見泰宏 - YouTube
皆さん、こんにちは。稲見 泰宏と申します。
本日は、この圏論シンポジウムという貴重な場でお話しさせていただくことをとても光栄に思います。
私の方からは、圏論とプログラミングに絡めた話について発表します。
それでは、どうぞよろしくお願いします。
まず簡単に自己紹介します。稲見泰宏といいます。
現在は、フリーランスのiOSアプリ開発者として活動しております。
ここに書いてあるのは、私の過去10年間のプログラミング経歴ですが、
PHPとJavaScriptを使ったWeb開発に始まり、iOSエンジニアに転向してObjective-C、
途中寄り道もしながらJavaを学び、そして現在はよりモダンなSwift言語と、趣味でHaskellを少しだけ書いています。
特にここ2年ほどは、より深くプログラミングを理解するために「圏論」を学んでいます。
元々は大学で物理学を専攻していて、最近はコンピュータ・サイエンス全般に興味があります。
- 圏論とSwiftへの応用 / iOSDC Japan 2018 - Speaker Deck
- プログラマのためのモナド(圏論) / #cat4pg - Speaker Deck
- Swiftプログラミングと論理 〜そして帰ってきた圏論〜 / Swift and Logic, and Category Theory - Speaker Deck
ちなみに宣伝になりますが、ここにあるリンク集は、私がここ1〜2年で、 プログラミングと圏論をテーマに発表した資料です。
今日の発表はこれらの発展形になりますので、もしご興味があれば、これらの資料もぜひチェックしてみてください。
さて、今日のテーマは 「圏論とプログラミング」 なわけですが、
よく聞かれるのが、 「一般のプログラマーは圏論を学んだ方が良いのか?」 という質問です。
これに対して、私はこのように考えています。
このスライドにあるのは、1990年代から2010年代にかけてのプログラミング言語の変遷です。
ご存知の通り、1990年代といえばまさに インターネットが大普及する時代 で、
この頃に登場した Webプログラミング (Python, Ruby, Java, JS, PHP) は
比較的小規模のアプリケーション開発が中心で、軽量なインタープリタ言語が人気でした。
しかし2010年代にも入ると、スマートフォンが大躍進し、
サーバーだけでなく手元のクライアントアプリも複雑な機能性が求められるようになりました。
それに伴い、プログラミング言語も、型付きで堅牢な言語が好まれるようになりました。
Rust, Kotlin, TypeScript, Swift などがそれらの代表的なモダン言語です。
これらの新しい言語に共通している点としては、
静的型付けであり、型推論が備わっていること、ジェネリクスがあること、
パターンマッチングができること、モナドの技術が使われている、などなどです。
つまり、この20年という時代の流れを一言でまとめるなら、
「型付きプログラミング」の台頭、ひいては**「関数型プログラミング」の台頭**といえます。
ここで、モナドといえば思い出すのは Haskell です。
そう、2010年代になって、ようやく時代がHaskellに追いついてきたと言っても過言ではありません。
しかし、そんなHaskellもまた大きく影響を受けているのが、この圏論です。
いわゆる矢印の理論ですが、プログラミングの世界だけでなく、
ありとあらゆる学問分野で用いられているのが特徴です。
プログラマーが圏論を学ぶと嬉しいことは、ざっとこのようになります。
特に実務の上で、型計算、設計、抽象化のスキルが上がるというのは、
これからますます型の重要性が問われる時代において、大きなポイントだと言えます。
さて、そんな圏論とプログラミングの深い関係ですが、
ここからは実際に、圏論がプログラミングにどのように影響を与え、
応用へとつながっていくのかを見ていきたいと思います。
本日のアジェンダはご覧の通りです。
若干詰め込みすぎて、駆け足にはなると思いますが、全体像を俯瞰してもらえればと思います。
プログラミング言語は、Haskellを使います。
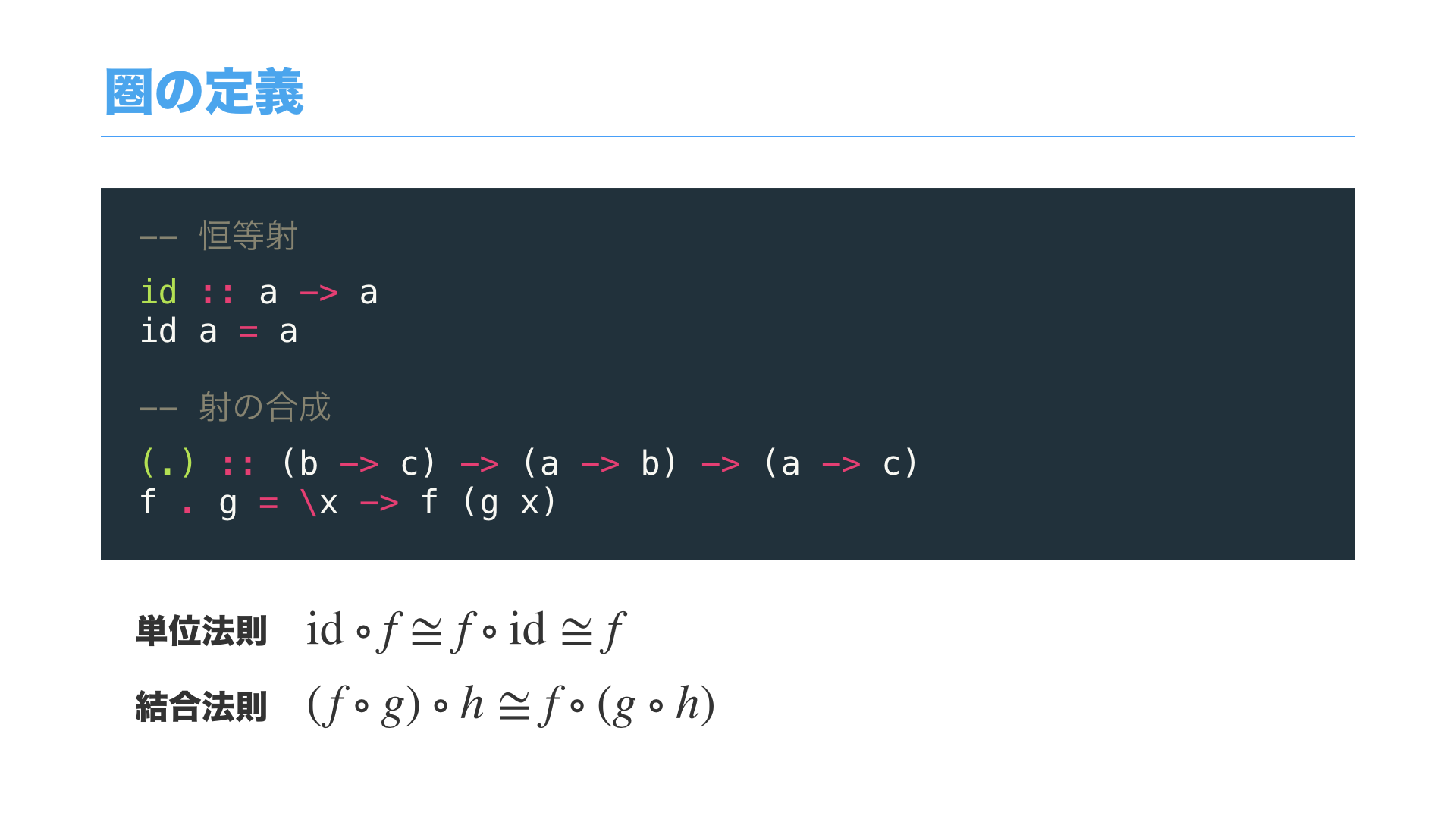
それでは、まずは圏の定義から見ていきましょう。
圏の定義は大まかに、恒等射idと 射の合成演算(.) (ドット) からなります。
これら2つをHaskellで書くとこのようなコードになります。
満たすべき性質としては、単位法則と結合法則が成り立つ必要があります。
ここで、Haskellには型クラスという便利な抽象化の機能があります。
他の言語でいうところの、「インターフェース」「トレイト」「プロトコル」と呼ばれるものです。
型クラスを使うと、まず class Category というものをこのように定義できます。
そして、この cat と書かれているところに「関数の矢印 ->」を代入すると、
先ほどの実装が、いわゆる型と関数の圏(Hask圏) のインスタンスとして再定義することができます。
このように型クラスを使う利点として、他にもさまざまな便利な圏を定義することができます。
例えば。。。
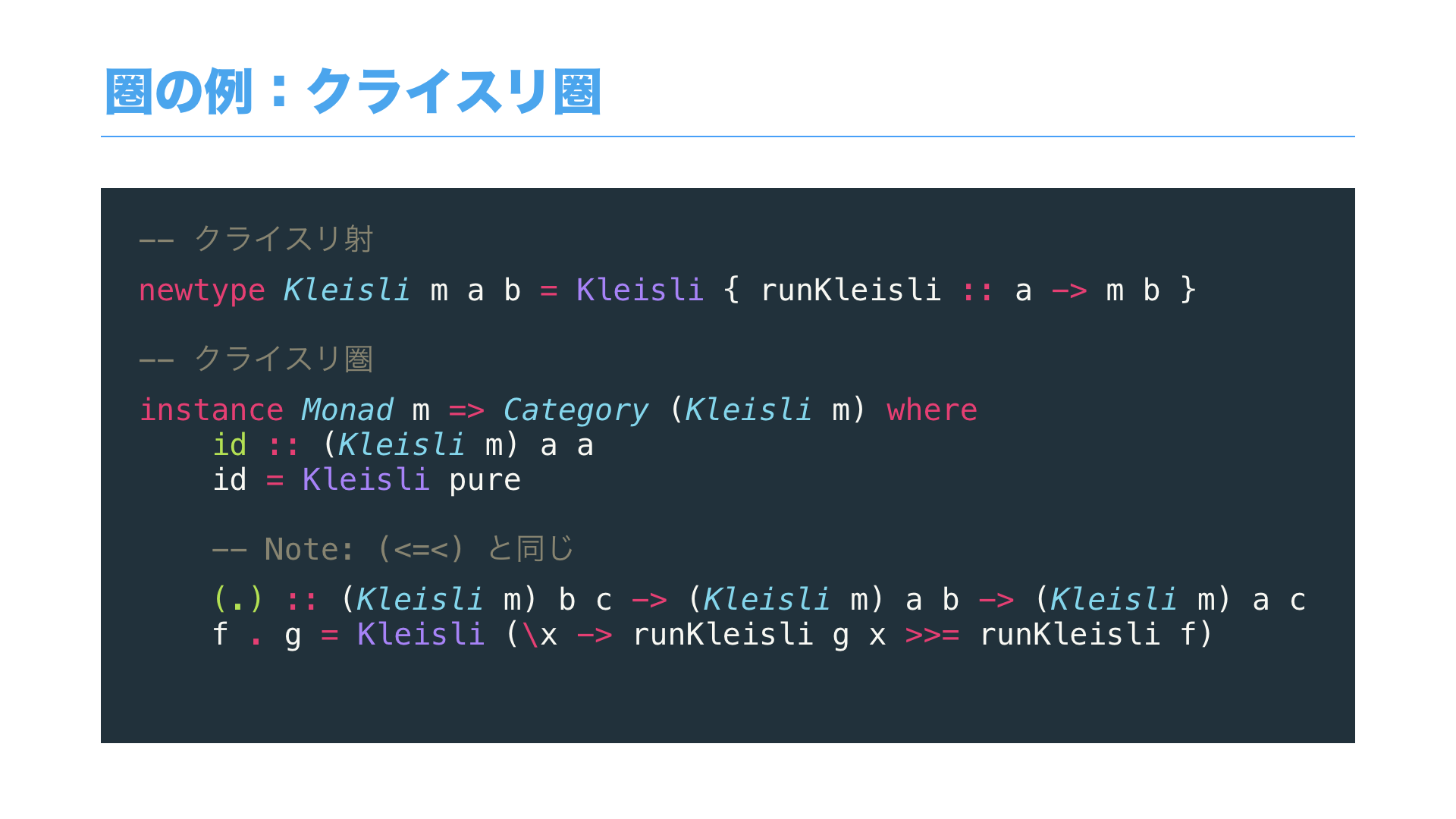
このスライドにあるクライスリ圏、いわゆる**「モナドに包まれた計算の射の世界」**というものを考えたり。。。
(参考:プログラマのためのモナド(圏論) / #cat4pg - Speaker Deck)
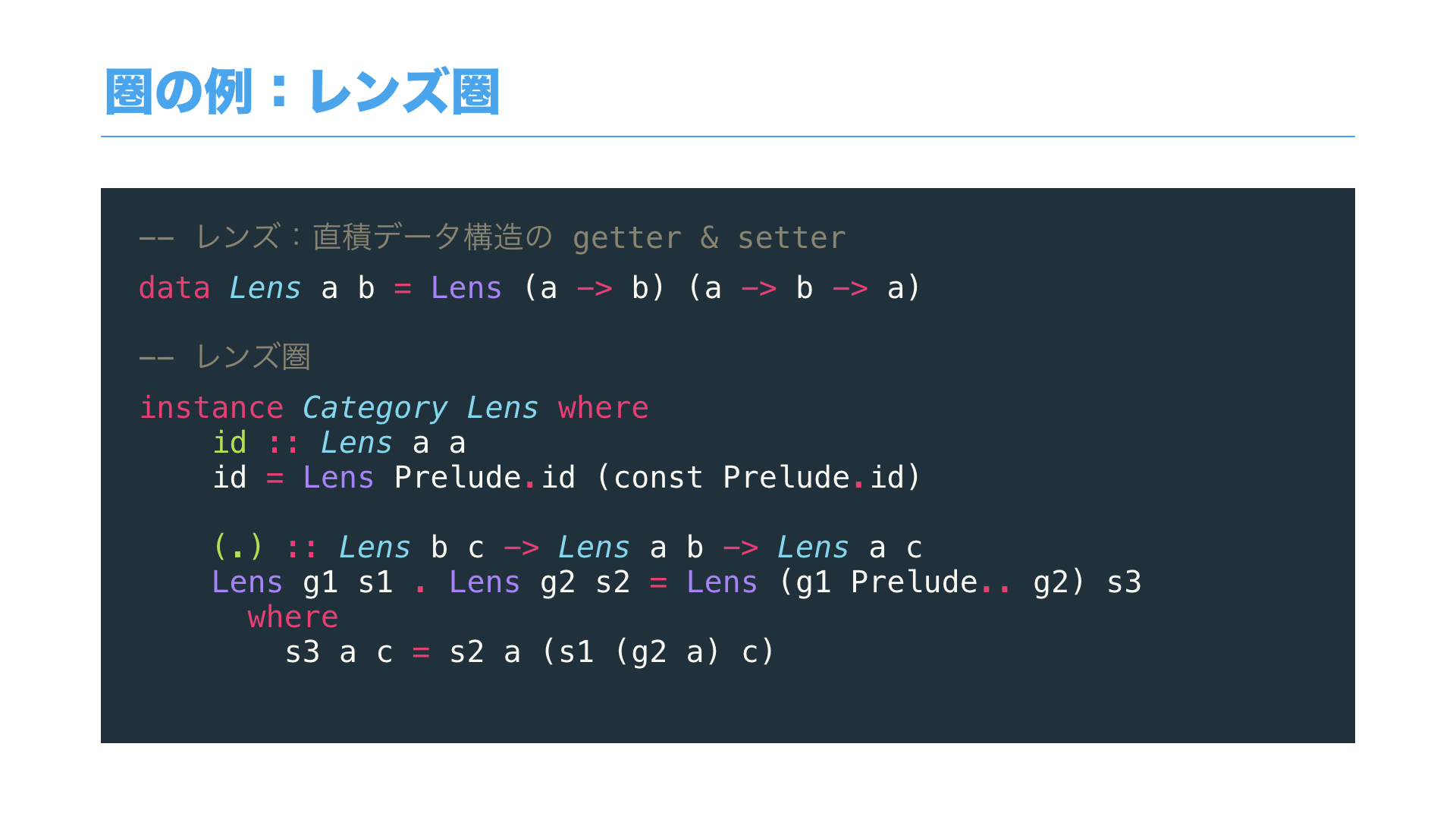
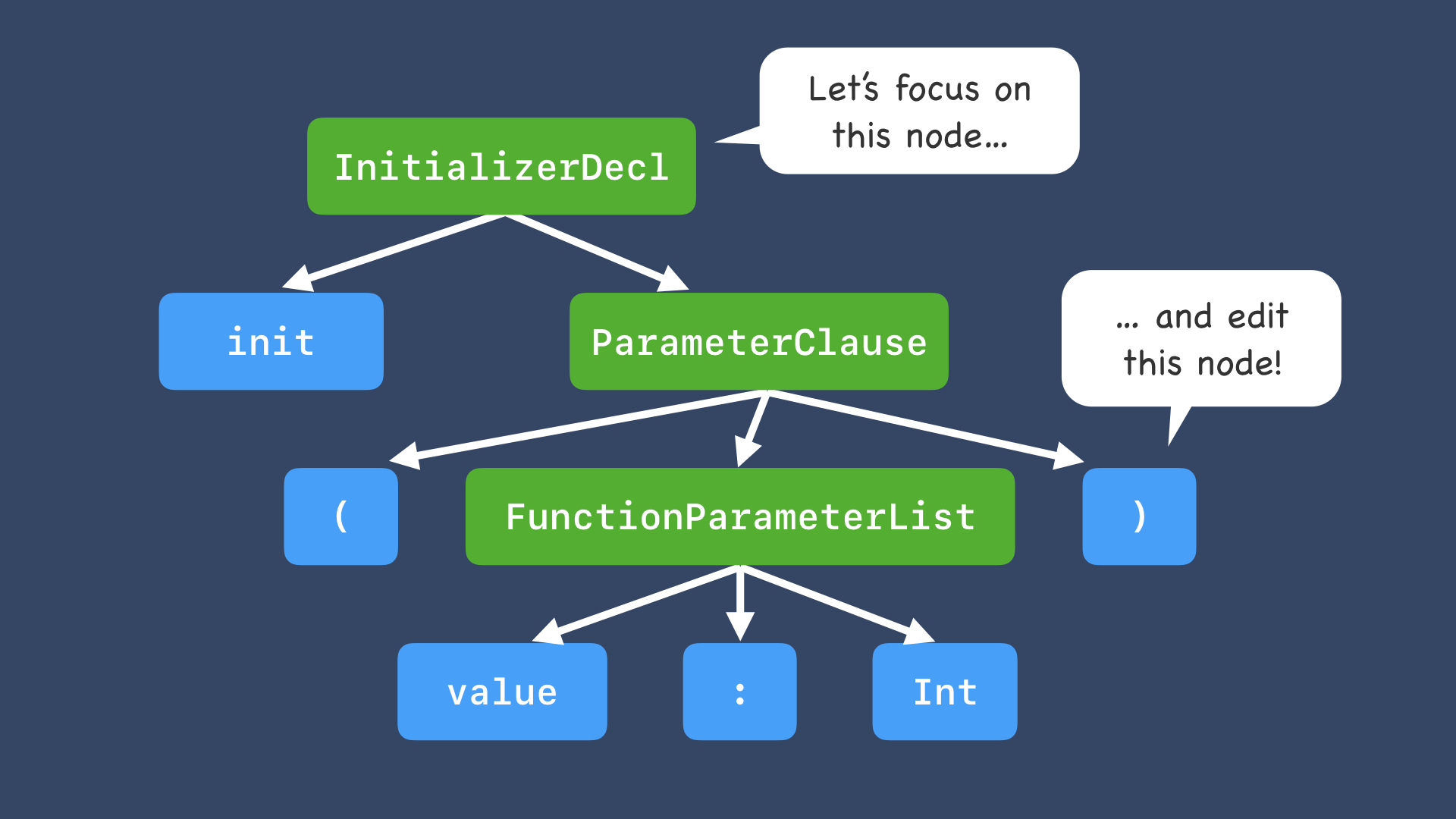
あるいはレンズという**「データ構造や内容にアクセスする機能の圏」**を作ることができます。
レンズについては、また後ほどご説明します。
以上が、圏の定義になります。
次に、関手を見ていきます。
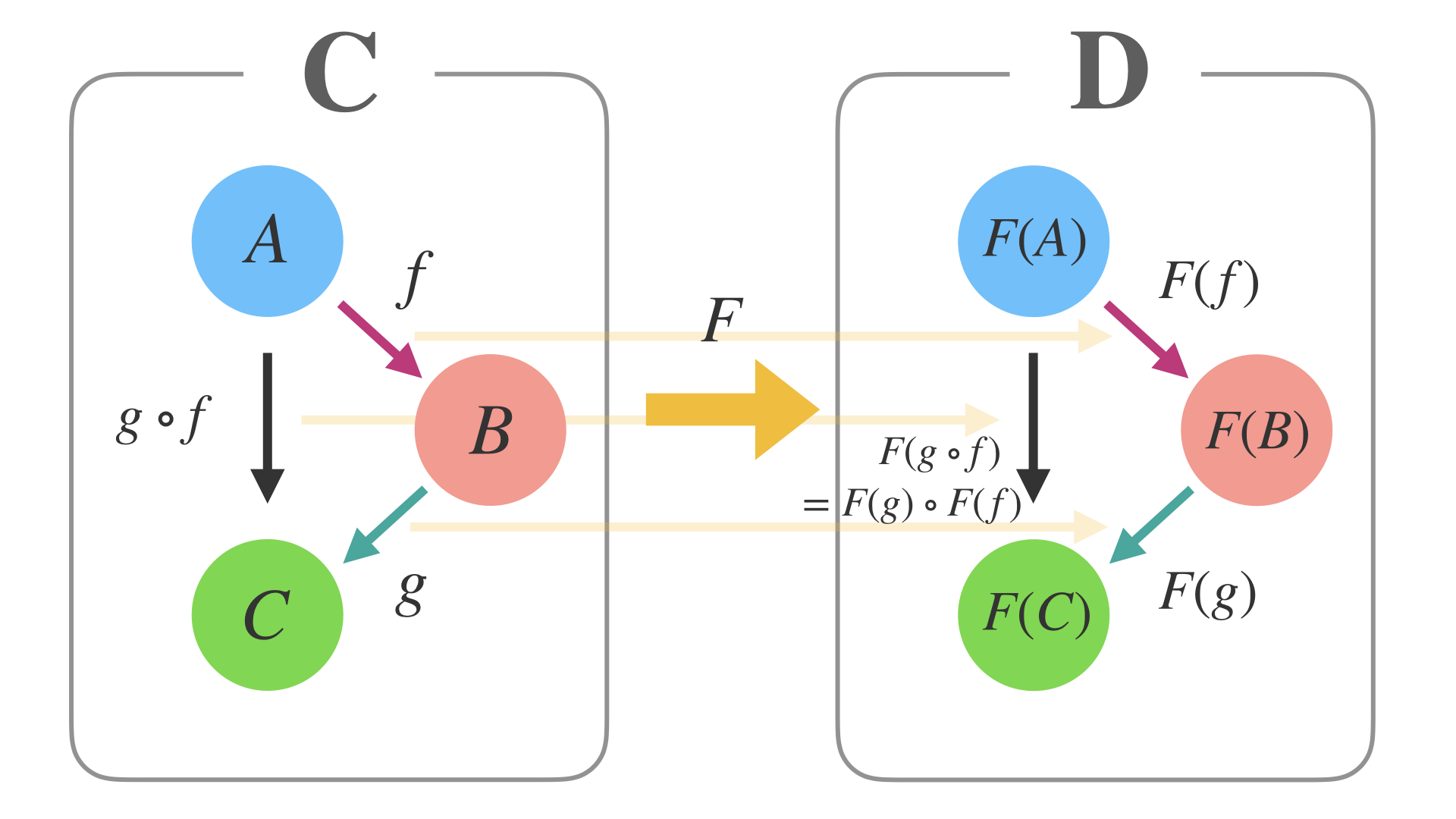
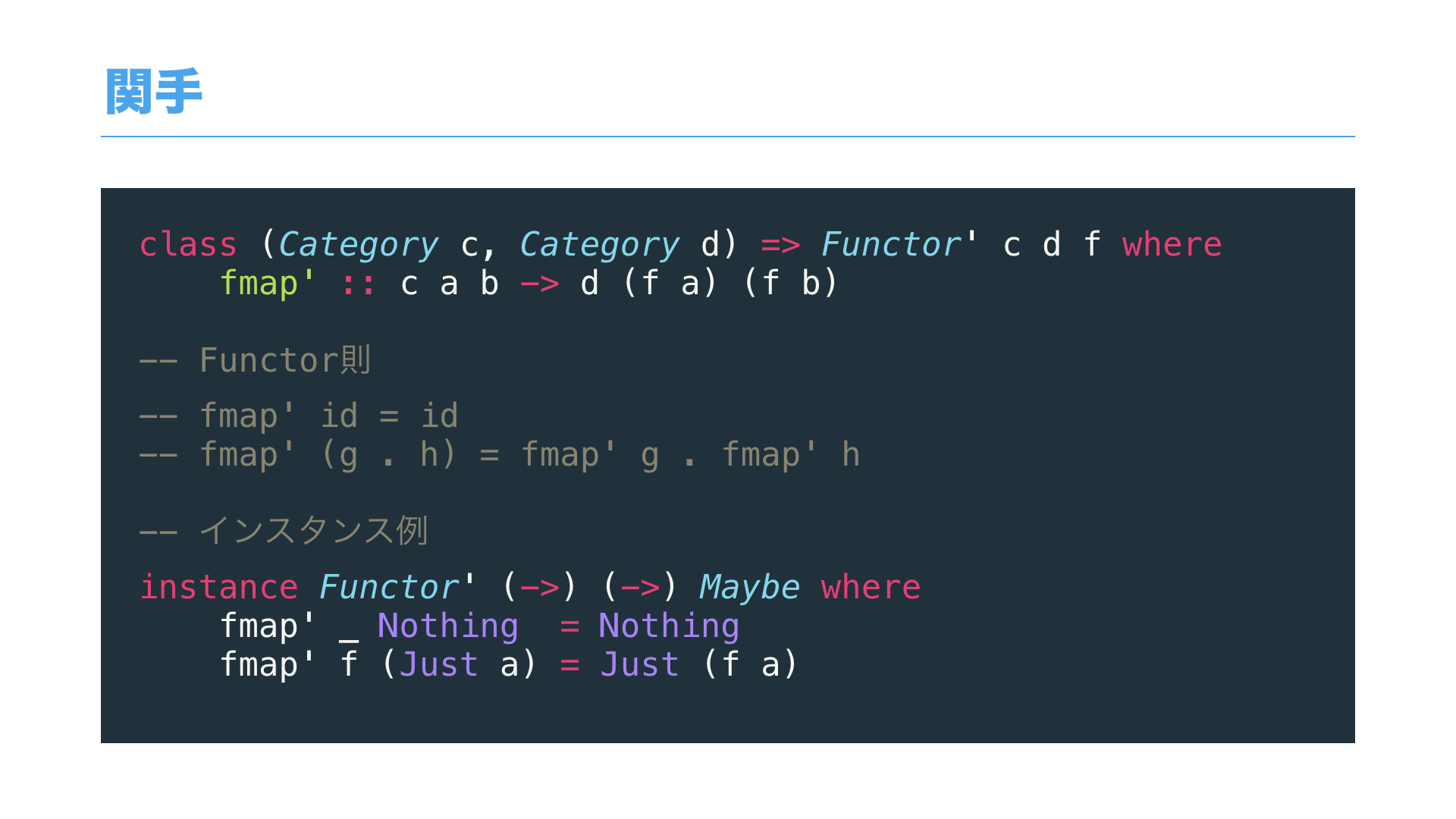
関手については、一言で言うなら、圏から圏へ、構造(形)を保つマッピングです。
これをHaskellで考えると、このようなコードになります。
読み方としては、まず圏CとDがある上で、関手Fについて考え、
圏CにおけるAからBへの射 c a b は、圏Dにおける f a から f b への射 d (f a) (f b) に写る、
それが fmap となります。
関手の例としては、2つの圏を同じHask圏として、Maybe型をこのように実装することができます。
ただ、通常のHaskellのコードでは、このFunctorはやや冗長で、実際のところは。。。
このように、Hask圏の自己関手の部分をまとめて Functor と呼ぶことがHaskellでは通例になっています。
つまり、HaskellにおけるFunctorは、圏論における自己関手のことです。
それでは続いて、関手圏と自然変換について見ていきます。
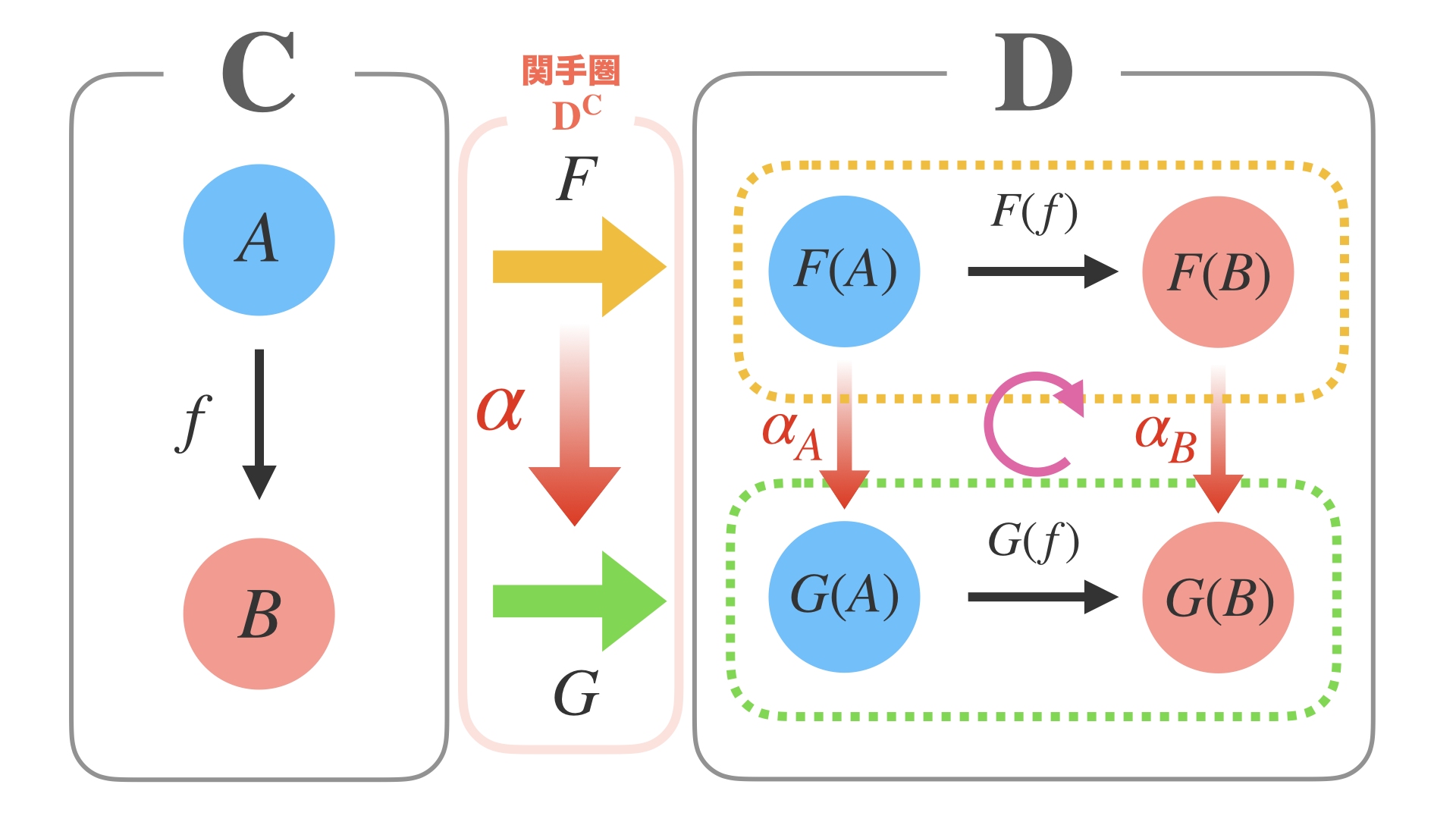
自然変換を一言で言うなら、2つの圏の間を流れる関手が2つあり、
さらにその間を流れる自然な射α、になります。
もしこの射が存在するならば、圏Dではいわゆる可換図式が成り立ちます。
自然変換は、プログラミングでいうところのジェネリクスに相当します。
すべての x についての、 f x から g x への射の族のことです。
このように自然変換を定義すると、自然変換もまた圏のインスタンスを構成することになります。
id は恒等自然変換、合成は自然変換の垂直合成になります。
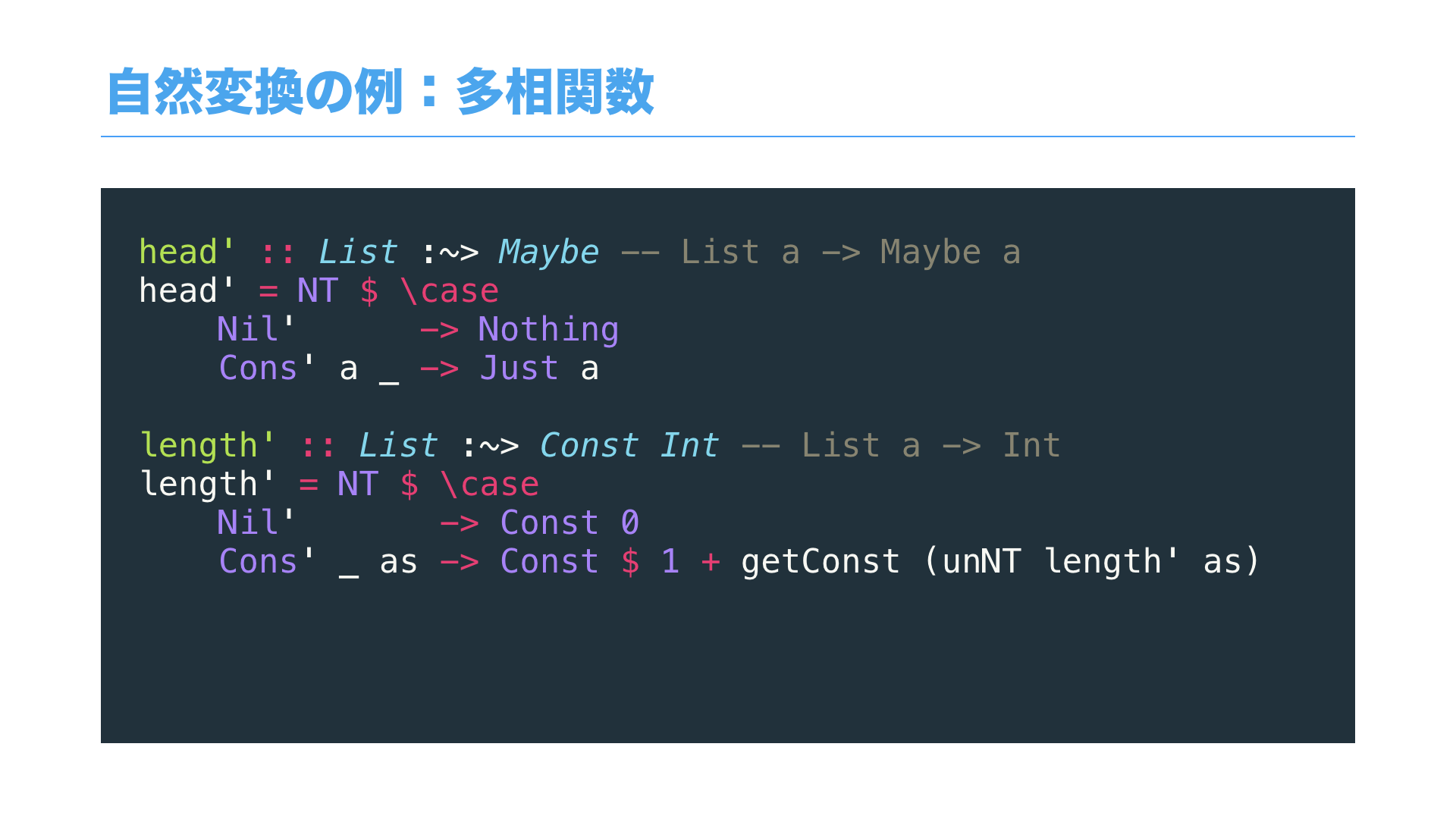
ここでは自然変換の例として、ジェネリック関数 head と length を考えてみましょう。
これらの関数は、「配列の最初の要素を取り出す」、ないし「全体の長さを計算する」ものです。
まず、head は List a から Maybe a への関数なので、a を無視して考えると、
List から Maybe への自然変換になります。
一方で、length は List a から Int の関数になりますが、これは一見すると、
返り値の型に関手が使われていないので、自然変換に見えないかもしれません。
しかし、ここで、Const という定数関手を使うアイディアがあります。
すると、実はこの関数もまた List から Const Int への自然変換で表せることが分かります。
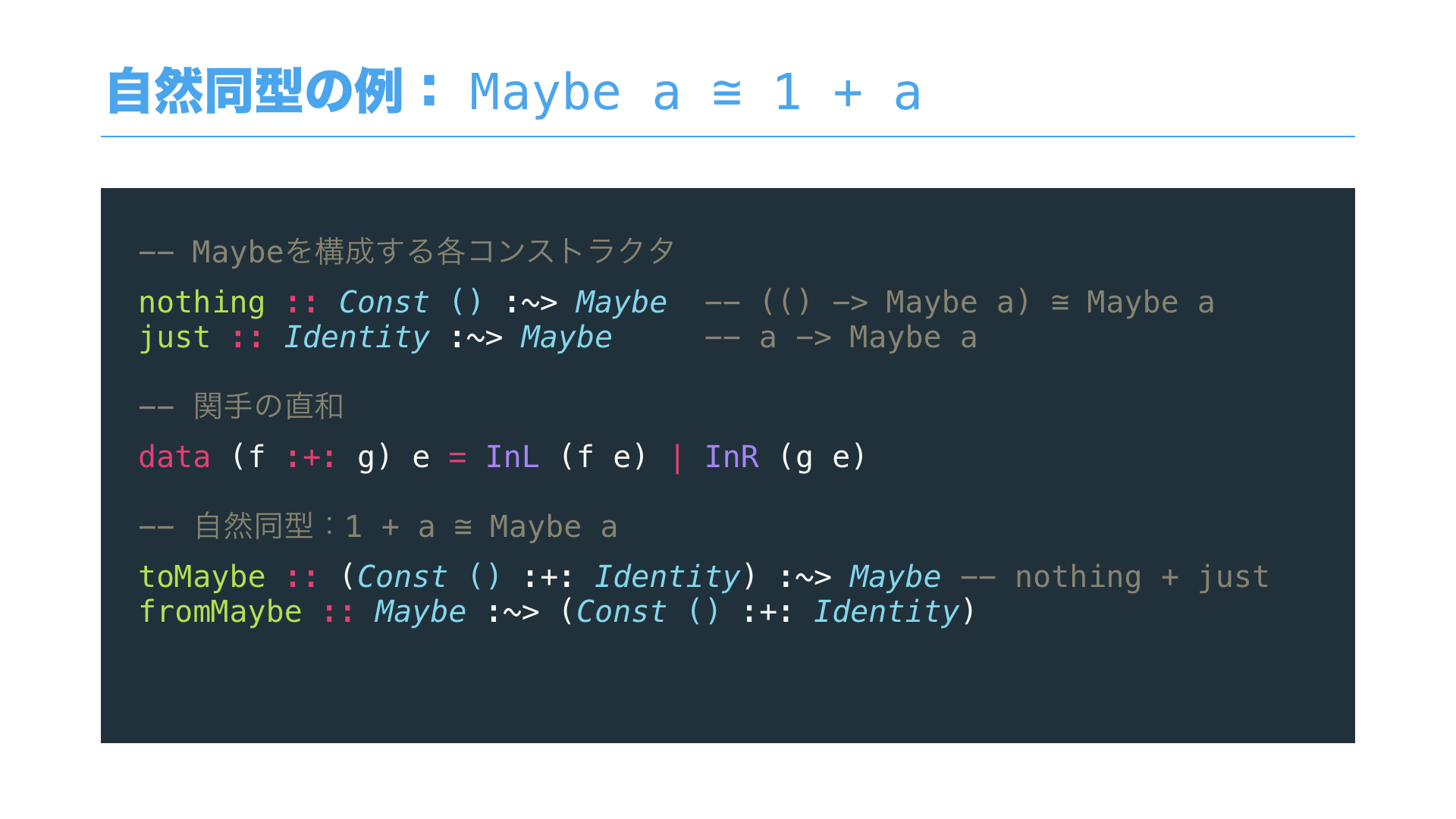
この定数関手を使った考えをさらに推し進めると、例えば、Maybe a は
nothing と just の2つのコンストラクタから構成されますが、
引数の型の関手はそれぞれ Const () と Identity で書け、
これらを関手の直和でつなげることで、Maybe と自然同型になります。
注目してもらいたいのは、この関手圏の世界ではもはや、プリミティブな型はほとんど登場せず、
関手とその射である自然変換が主役になっているのが分かります。
これはまさに圏論で最も重要な**「関手と自然変換」**が成し得る世界観ですね。
Haskellではこれが美しく書けます。
ちなみに、関手の直和を取る話は、モナドの計算効果を重ね合わせるための、
関手をベースとした足し算の話にもつながってきて、考え方としてとても重要になります。
それでは次に米田の補題を見ていきます。
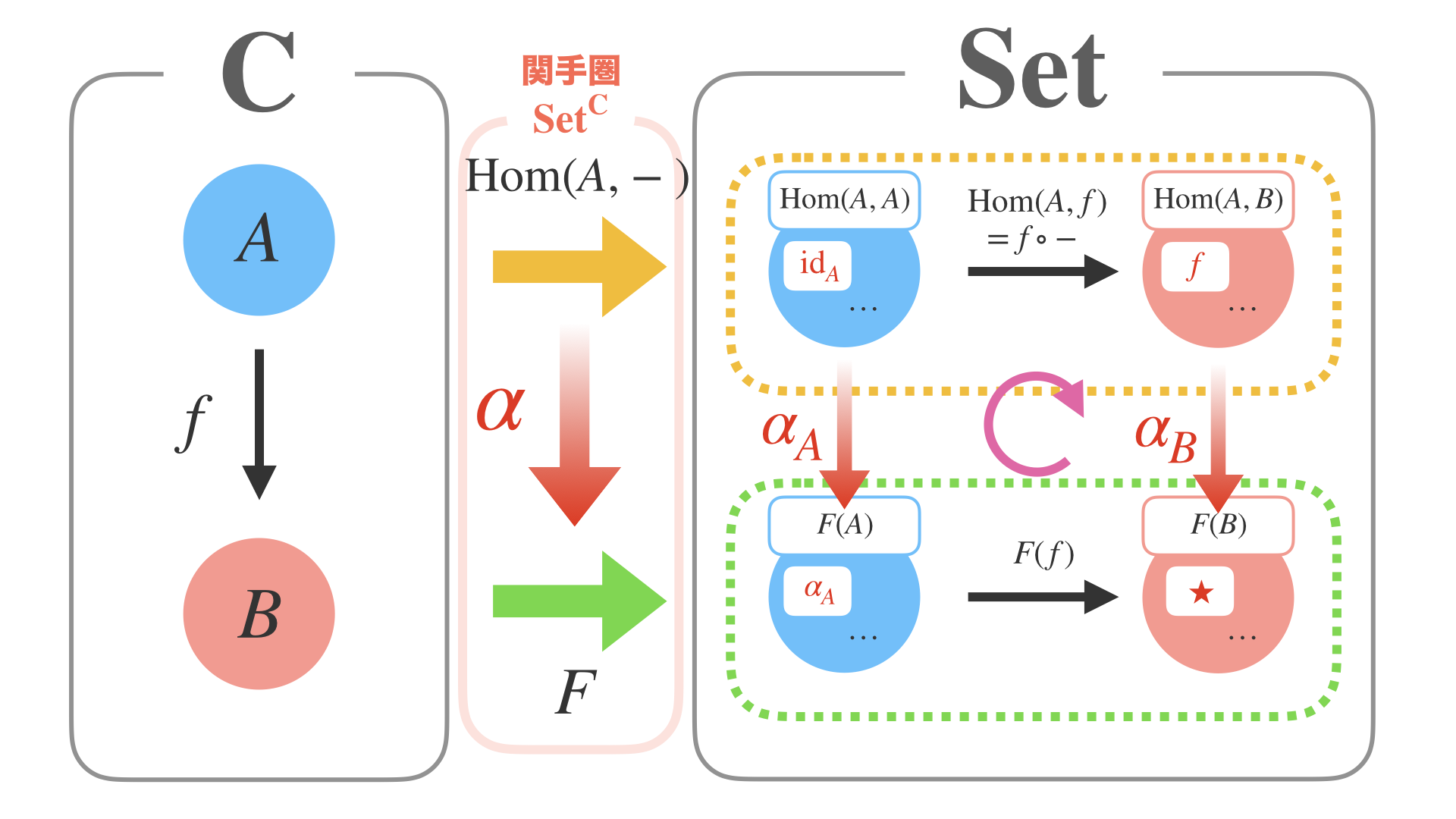
米田の補題は、先ほどの自然変換の図式で、右側の圏にSet圏を考え、
関手としてHom関手を使うと、自然変換αの集合とF(A)が1:1に対応するというものです。
それを圏論で表現するなら上の式のようになります。
米田の補題の有名な例としては、Fに恒等関手をおいたCPSと呼ばれる継続であったり、
さらには米田埋め込みがCPS変換に対応して、末尾再帰最適化などに使われています。
このスライドでは、newtype YonedaというものがHaskellに存在するので、
その中身を覗いてみると、実はそれが左辺と同じ形になるのが分かります。
ここで、米田埋め込みと米田の原理をおさらいすると、このようになります。
特に米田の原理は、型プログラミングの世界において、型計算の証明で役に立ちます。
例えば、$(A^B)^C$ (c -> b -> a) を型計算したときに
$A^{B×C}$ ((b, c) -> a) と同型であることが米田の原理から簡単に証明できます。
これは、単純な指数法則の1つではありますが、
型の世界でも全く同じように成り立つのはとても驚嘆に値します。
ちなみに、米田の補題から得られる別の形として、Coyonedaと呼ばれる双対の形が挙げられます。
Haskell で表すとこのような形になりますが、この積分記号は圏論でいうCoendというもので、論理学でいう存在量化子(∃)だと思って下さい。
先ほどのYonedaとの違いとしては、lift時(右辺から左辺への変換時)に、fが関手である必要がない、という点です。
lift 後のCoyonedaは関手なので、言い換えるなら、何もないところから関手ができるということになります。
これに加えて、いわゆるフリーモナドというものを組み合わせると、
何もないところからモナドができる、という面白いテクニック (Freer Monad) が使えます。
というわけで、このYoneda / Coyoneda をまとめると、共変・反変バージョンを含めて
合計4つの同型の式が得られますが、実はこれらもおいおい型計算で大いに役立ってくれます。
ぜひとも覚えていってもらいたい式です。
さて、どんどん先に進めます。次は随伴です。
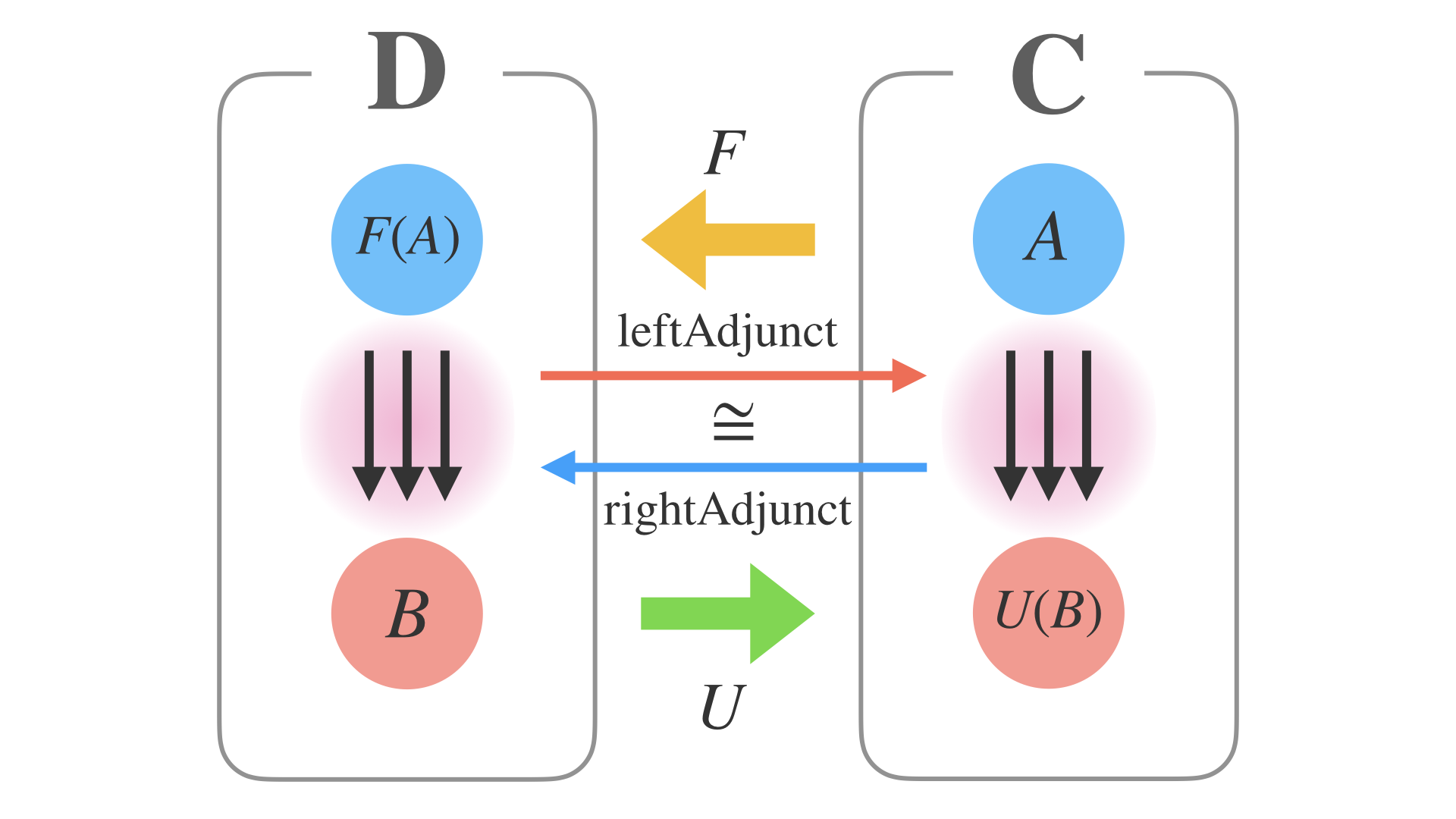
随伴は、2つの圏について双方向に伸びる2つの関手があって、
このスライドのピンクの部分の射集合が同型であることを定義とします。
この場合、左の射集合から右への leftAdjunct 関数、
ないし逆変換の rightAdjunct 関数を定義することが、随伴になります。
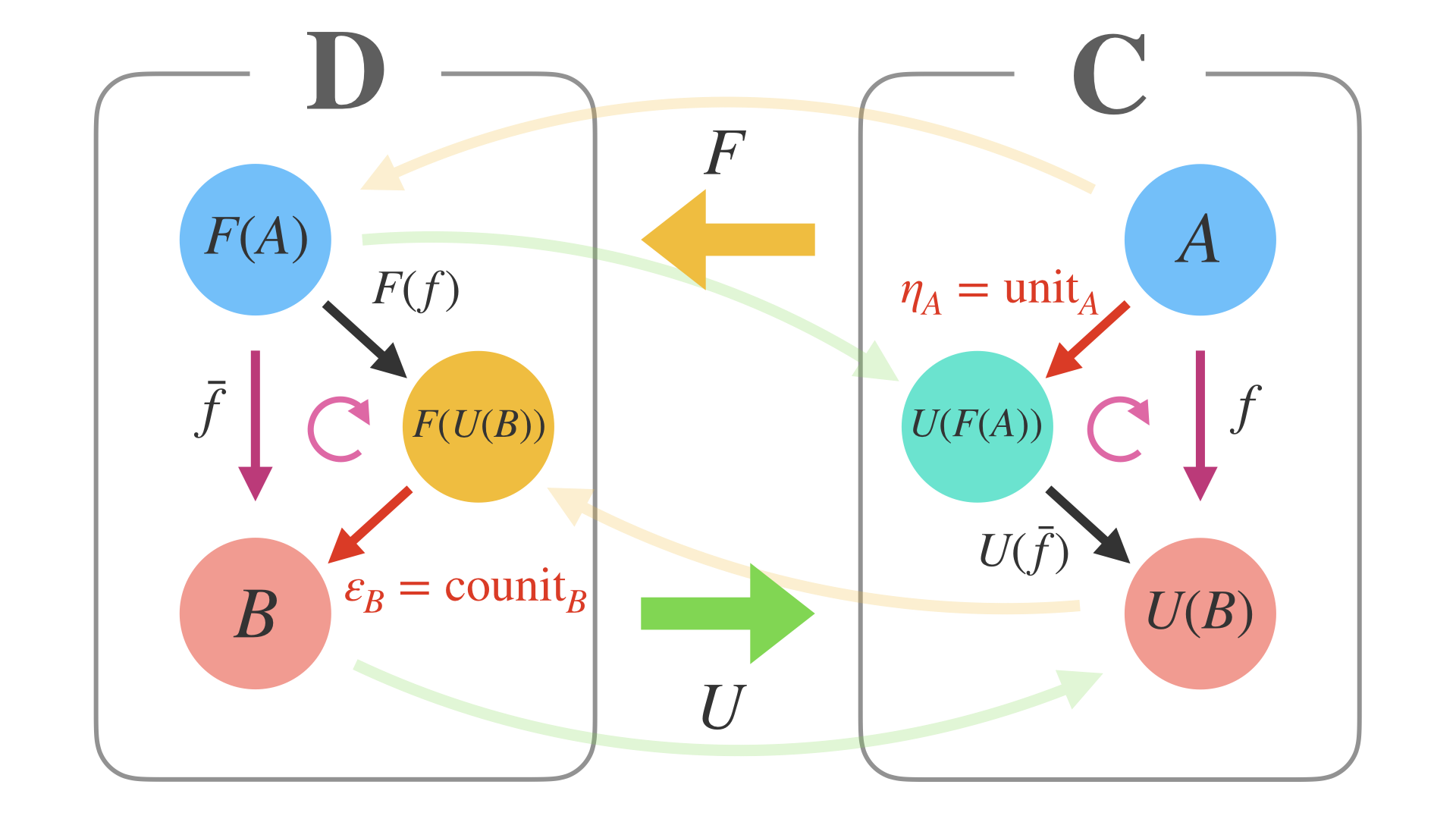
ちなみに、leftAdjunct / rightAdjunct の代わりに、
この図式のように**unit と counit**を定義しても随伴になります。
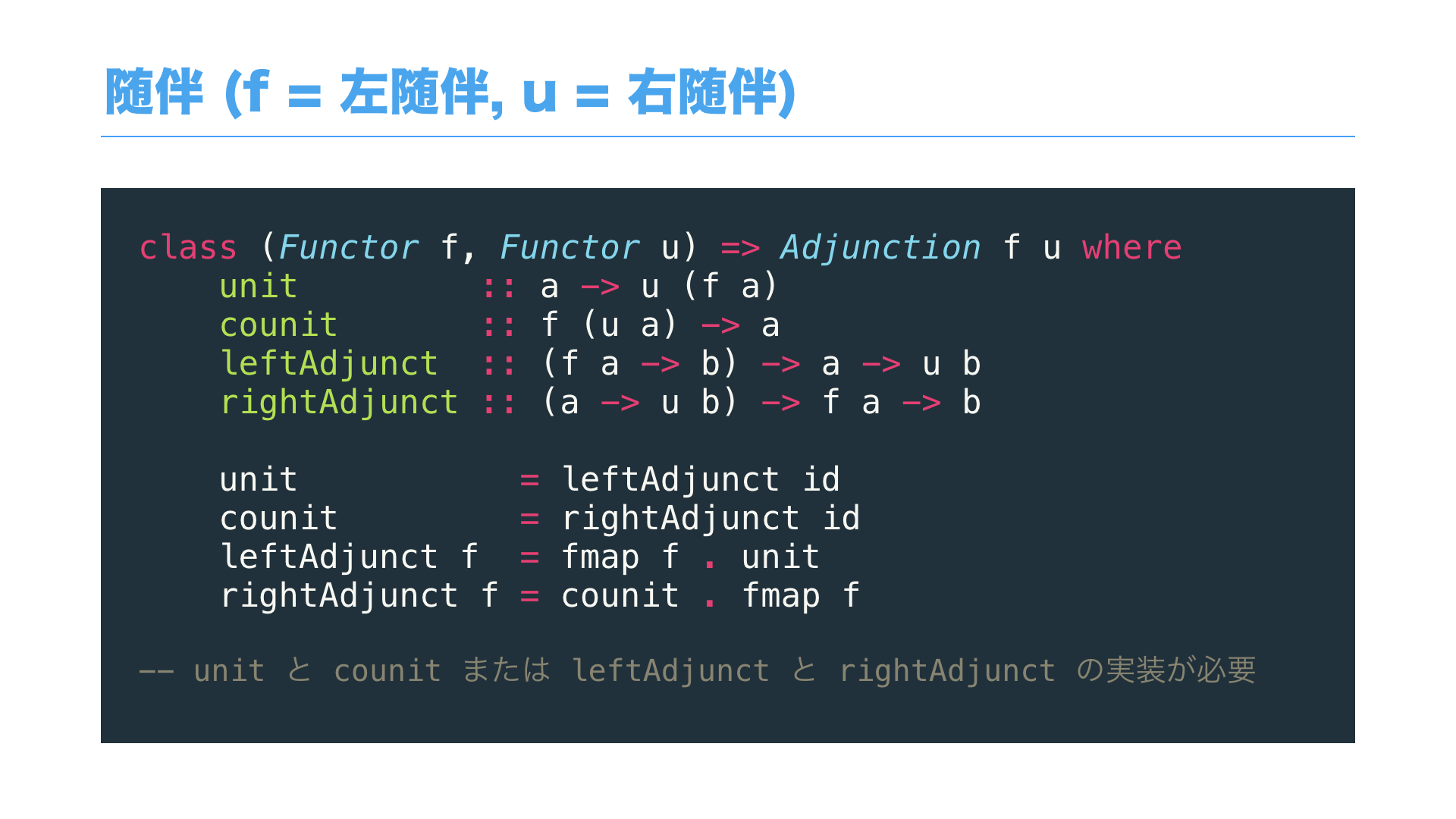
以上のことをHaskellで記述すると、このように書けます。
実はこのコード、なかなか驚くべきことで、並大抵のプログラミング言語ではこの実装がまずできません。
なので、この点においてもHaskellは強力で読みやすく、圏論と極めて親和性が高いといえます。
随伴の代表例としては、いわゆる直積と冪の随伴関係があります。
これをHaskellで書くと、このようになりますが、実装の中身は、いわゆる curry 化と uncurry 化に相当します。
curry 化は2引数関数を1変数の高階関数に変換するという点で、関数型プログラミングでは定番の機能です。
もうひとつ例としては、クライスリ圏への埋め込み関手と拡張関手というものがあります。
これは、少し複雑なバージョンのAdjunction型クラスを使うと、このように書くことができます。
他にも様々な随伴の例がありますので、こちらの記事を参考にしてみて下さい。
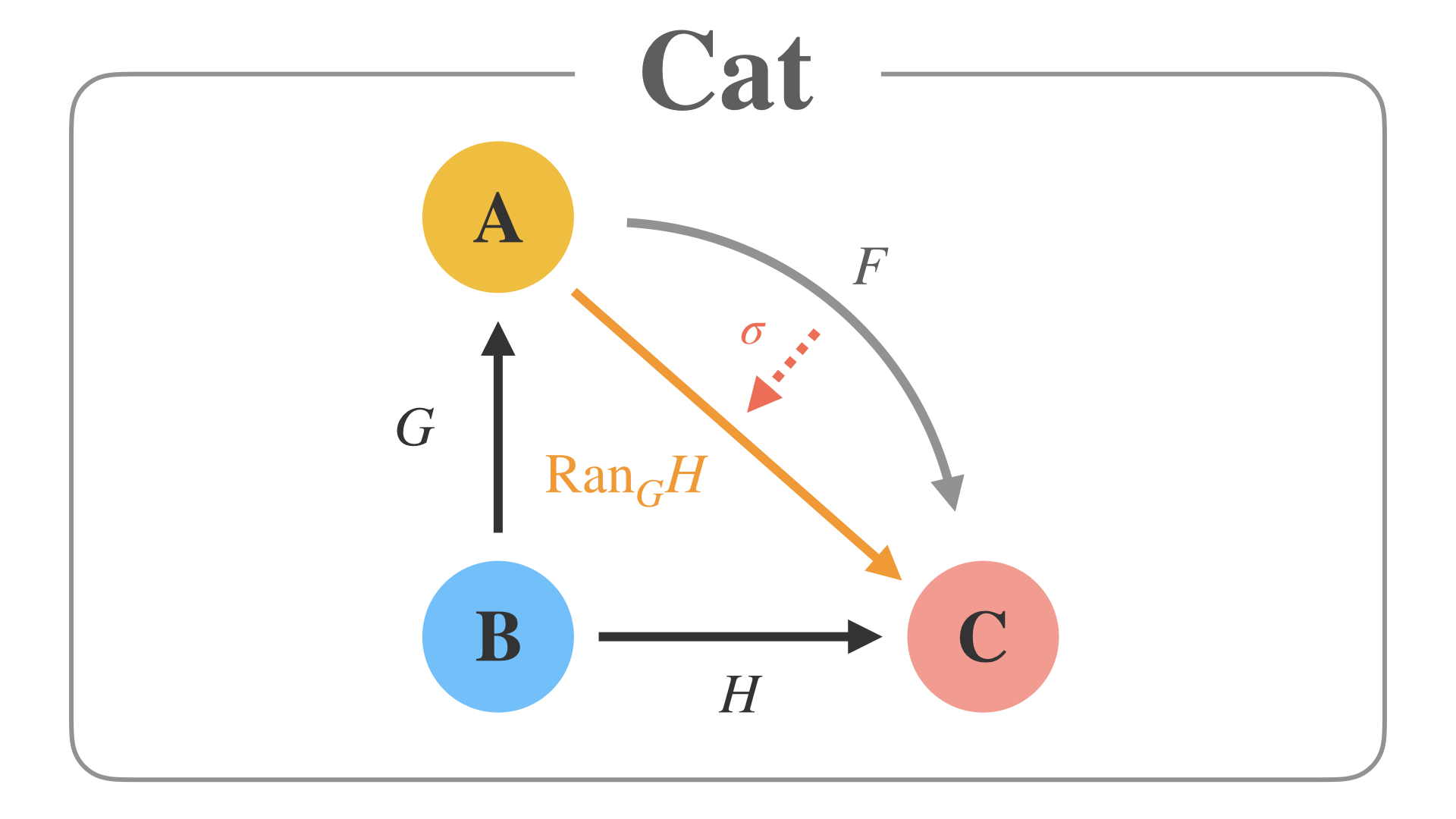
はい、そしていよいよ、全ての概念である Kan拡張 についてみていきます。
Kan拡張は、3つの圏A、B、Cと、2方向に伸びる関手G、Hがあるとき、
AからCに伸びるオレンジの射を考えるときに使います。
もしそのような普遍的な関手があると仮定したとき、他のどんなFを考えても、σの一意な自然変換が存在する。
この場合、オレンジの射のことを 右Kan拡張 といいます。
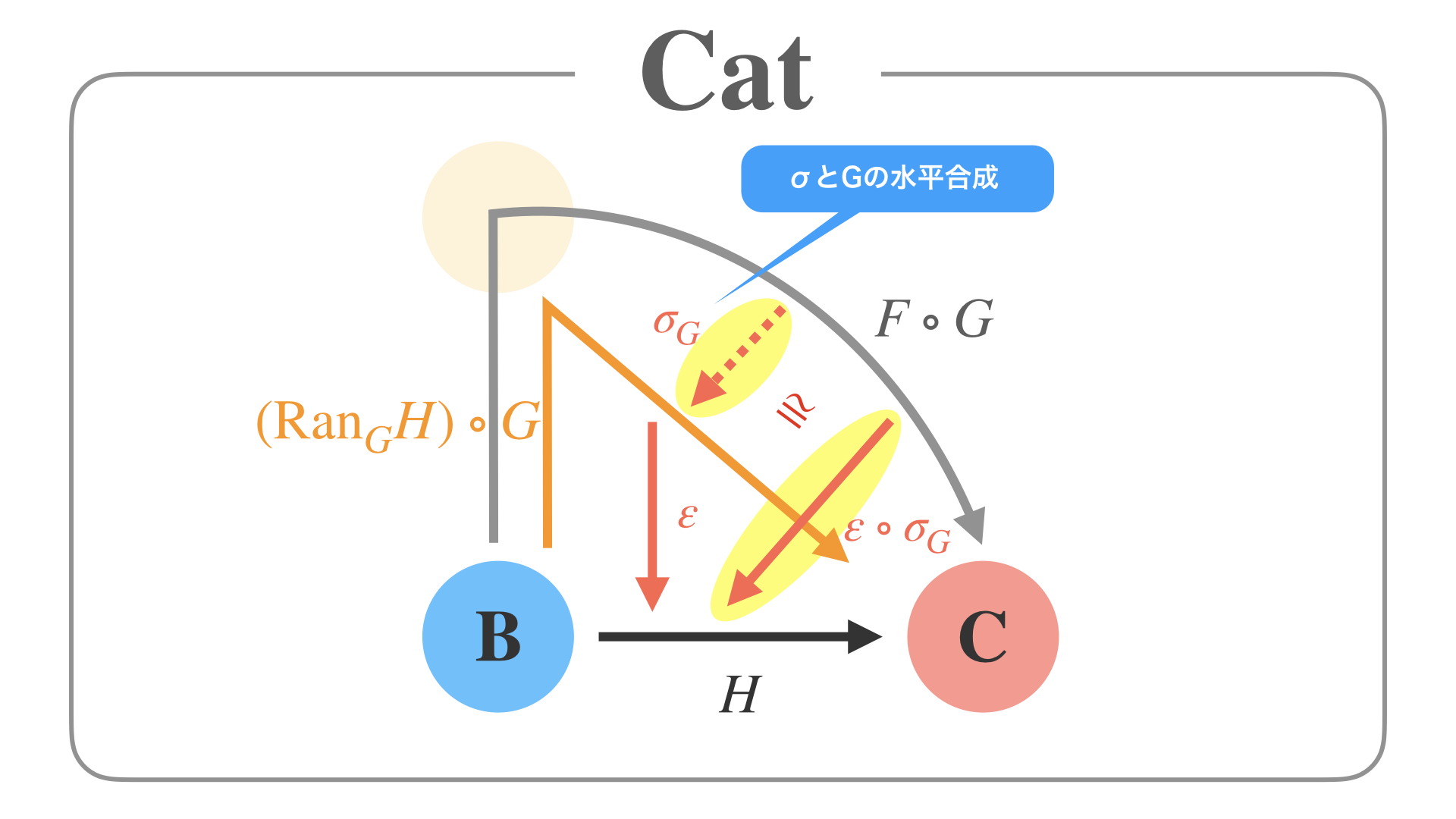
このとき、黄色で塗られた2つの射の集合を考えると、これらは同型になります。
ここに、ある種の随伴関係が見て取れます。
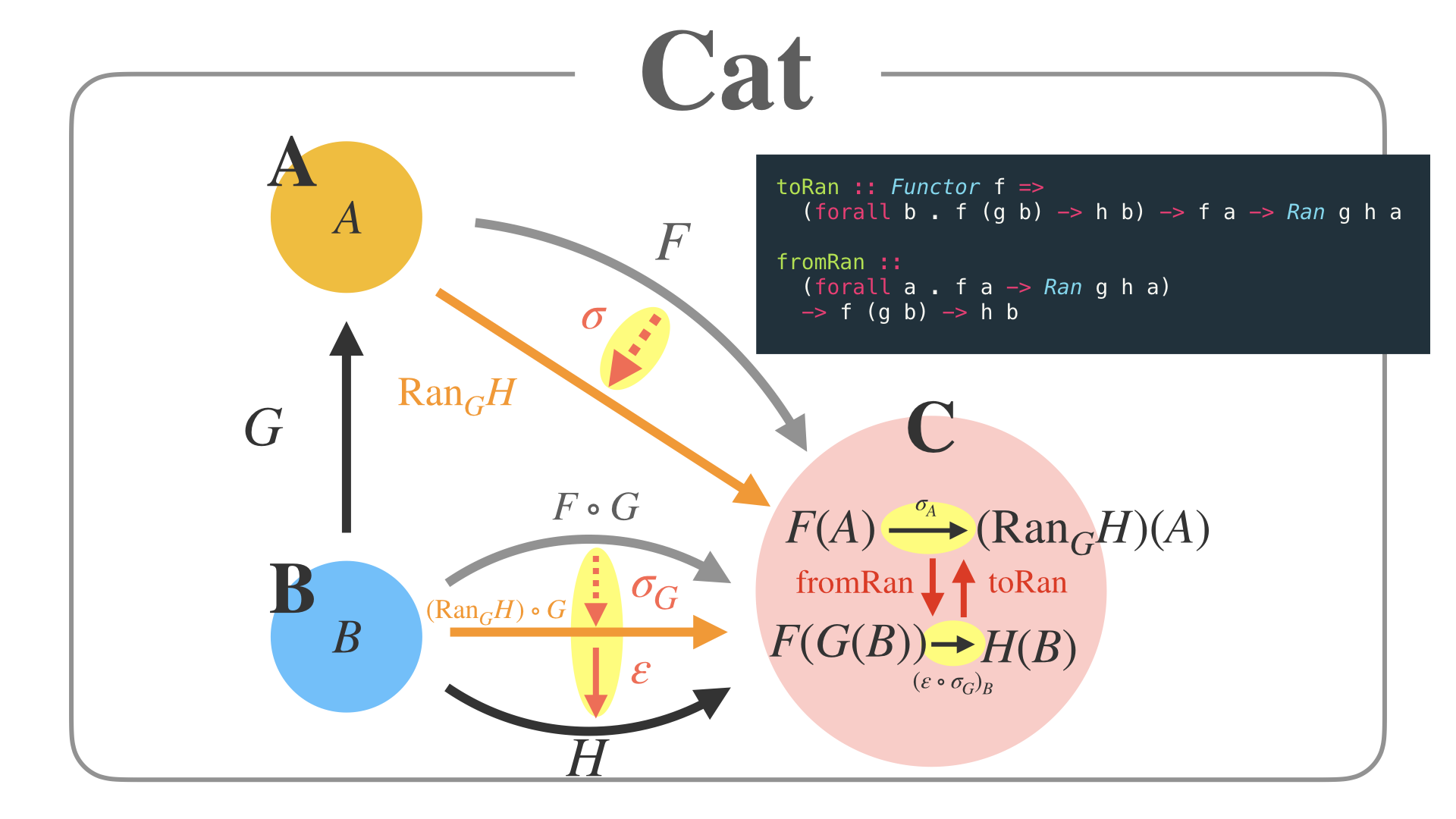
以上をまとめて、圏Cの中身を展開してみると、このような図が書けます。
そして、やはりCの内部の黄色い射集合も同型になります。
ここで、Haskellには、toRan / fromRan という関数があるのですが、
この圏Cの中にある双方向な射がまさに、それら2つの関数に対応しているのが分かります。
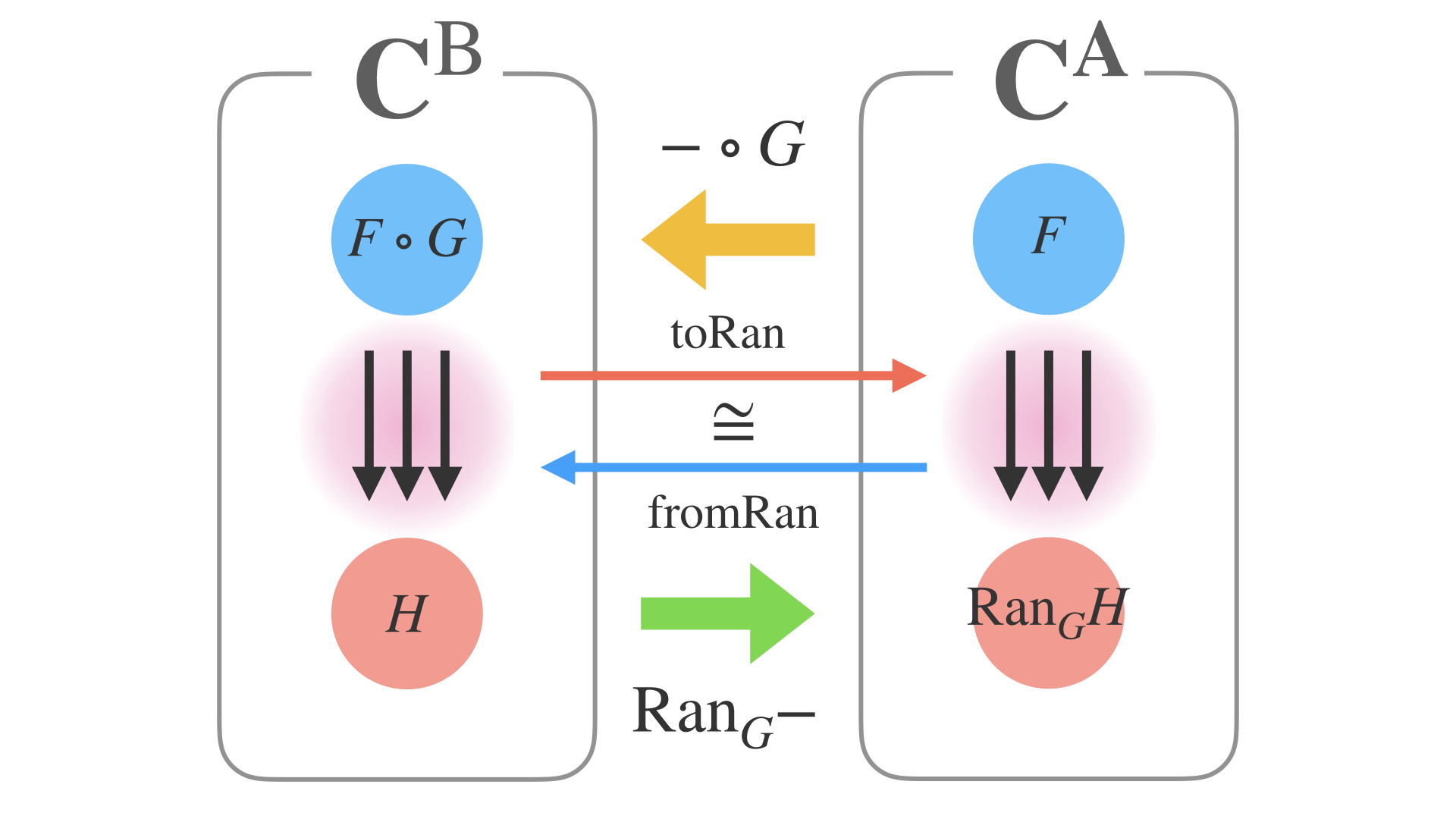
今の話を随伴部分だけ抜き出すと、このようにもう少し簡単に書けます。
スッキリ分かりやすくなったとも言えますし、逆に抽象度が上がりすぎて、初見殺しと言えるかもしれません。
これらの結果を Haskell (kan-extensionsパッケージ) で書くとこのようになります。
実は、右Kan拡張というのは、極限、右随伴、さらにはYonedaを内包した型になっており、
確かに変換する関数群が備わっているのが分かります。
それに対して、左Kan拡張というのは、右Kan拡張の双対、すなわち 余極限、左随伴、Coyoneda を内包しています。
ちなみに私はHaskellを学び始めたとき、このワンライナーのコードの意味がさっぱり分からず苦い思いをしましたが、
圏論を学ぶことでようやく読めるようになりました。
さて、ここまでが一応基本編ということで、
この先は実際のプログラミングへの応用編に移りたいと思います。
まずは、モナドとコモナドから。
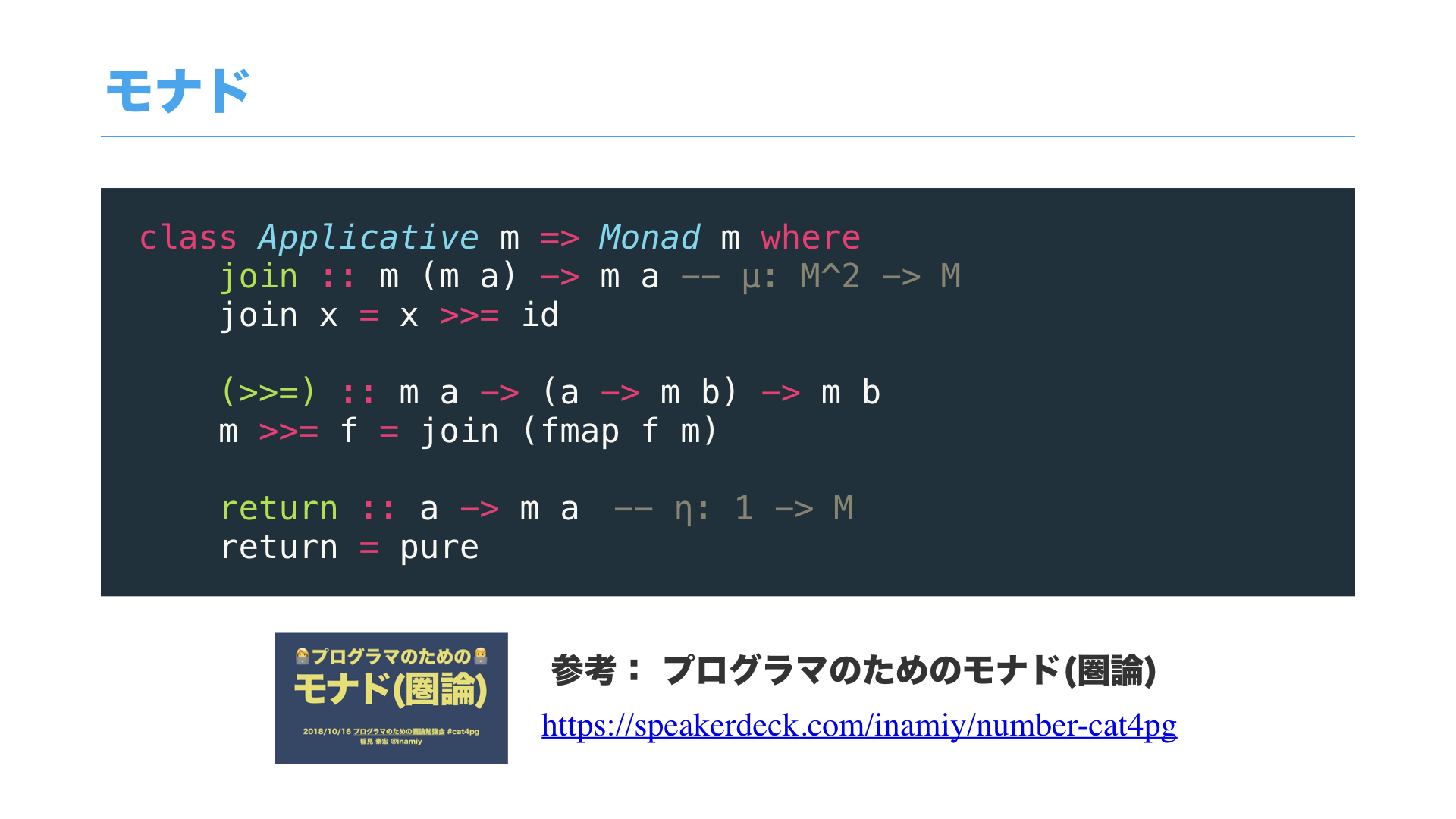
モナドについては、Haskellで書くとこのような型クラスで記述できます。
こちらに関しては、一昨年に、私が詳しく解説した別の登壇資料があるので、今回は説明を割愛したいと思います。
参考: プログラマのためのモナド(圏論) / #cat4pg - Speaker Deck
ただ1点だけ、随伴を使ったモナドの表現をお見せします。
このコードは、先ほどの**「直積と冪の随伴」からモナドを作った場合を示しています。
実はこの構成は、いわゆるStateモナド**というものに相当します。
やっていることとしては、左随伴→右随伴の往復を2セット行うと、
あっという間にモナドが出来上がるという仕組みです。
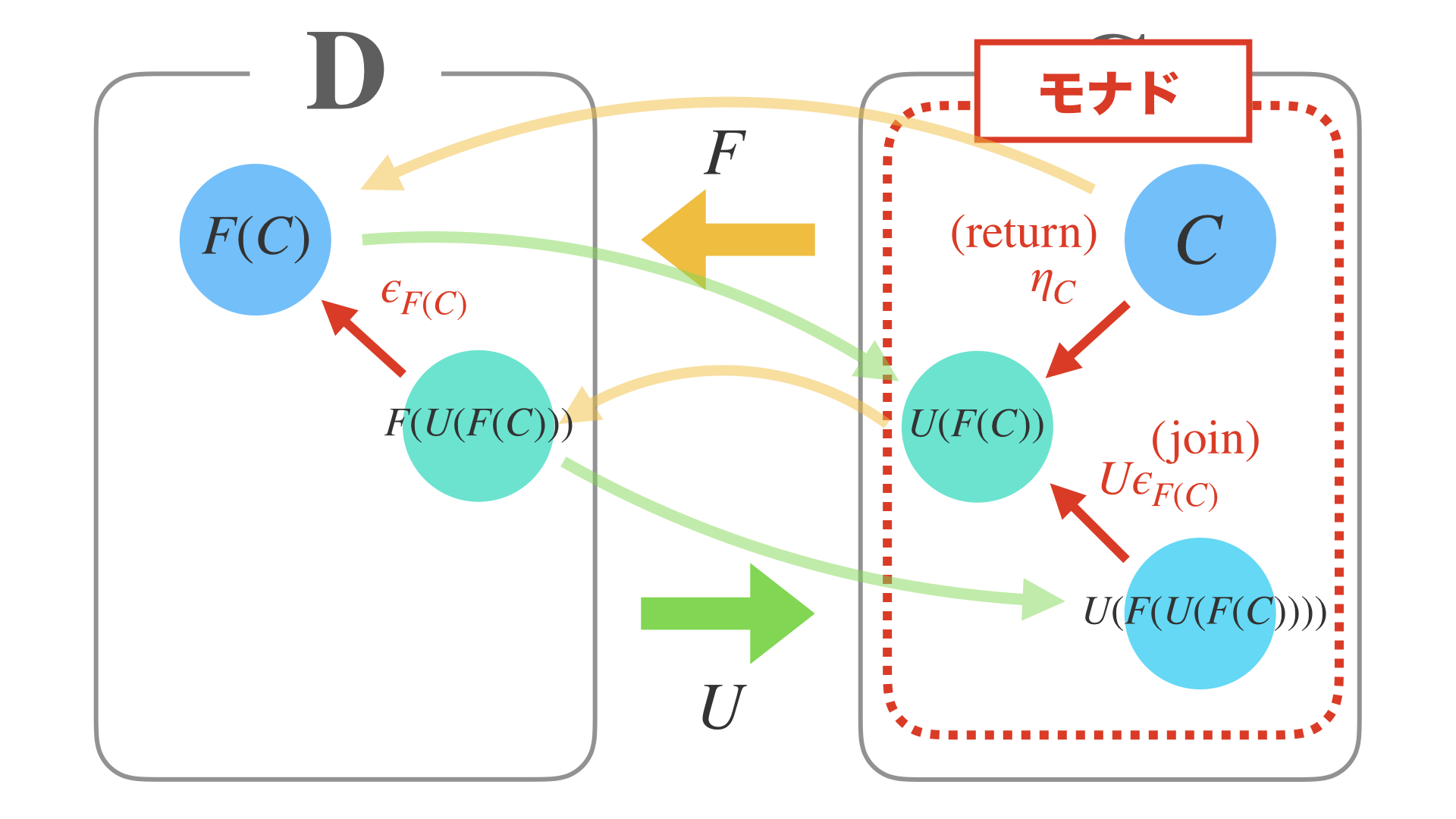
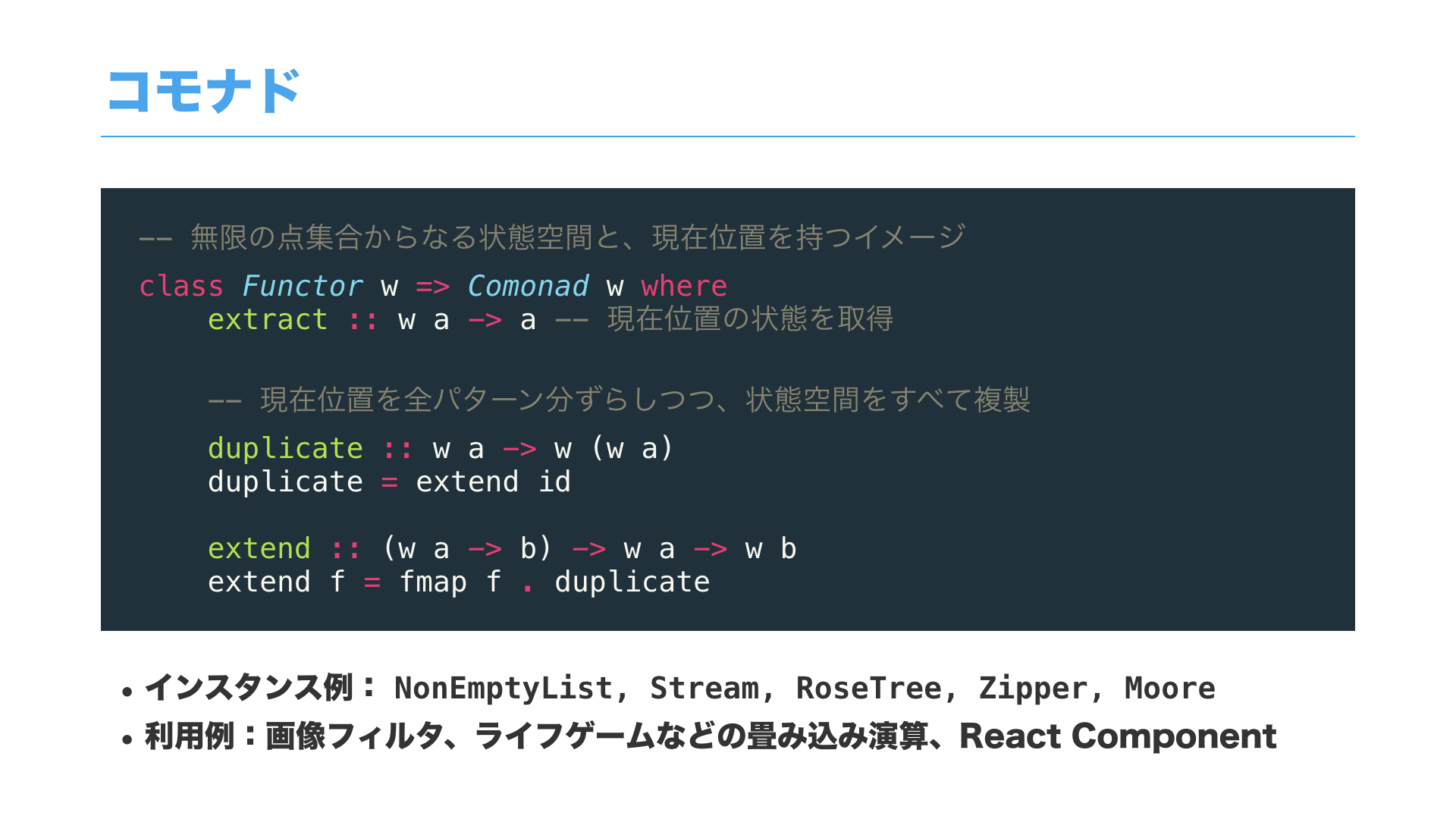
そして同様に、コモナドについても随伴から考えることが可能です。
ちなみに、このスライドのコードは、Haskellでよく見かけるComonad型クラスです。
利用例としては、画像処理やライフゲーム、あとWebフロントエンド開発で有名な React のComponentなどもコモナドになります。
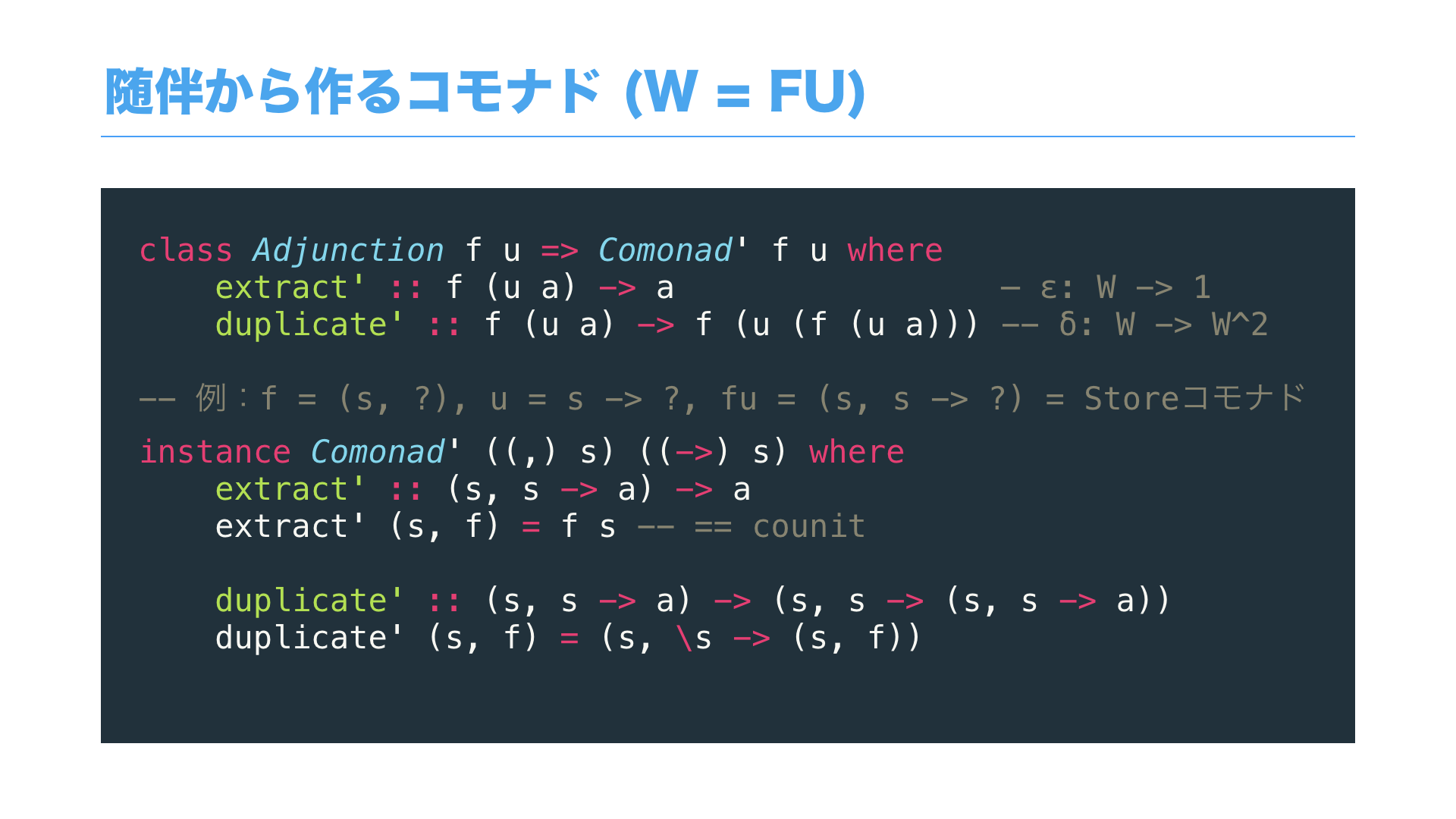
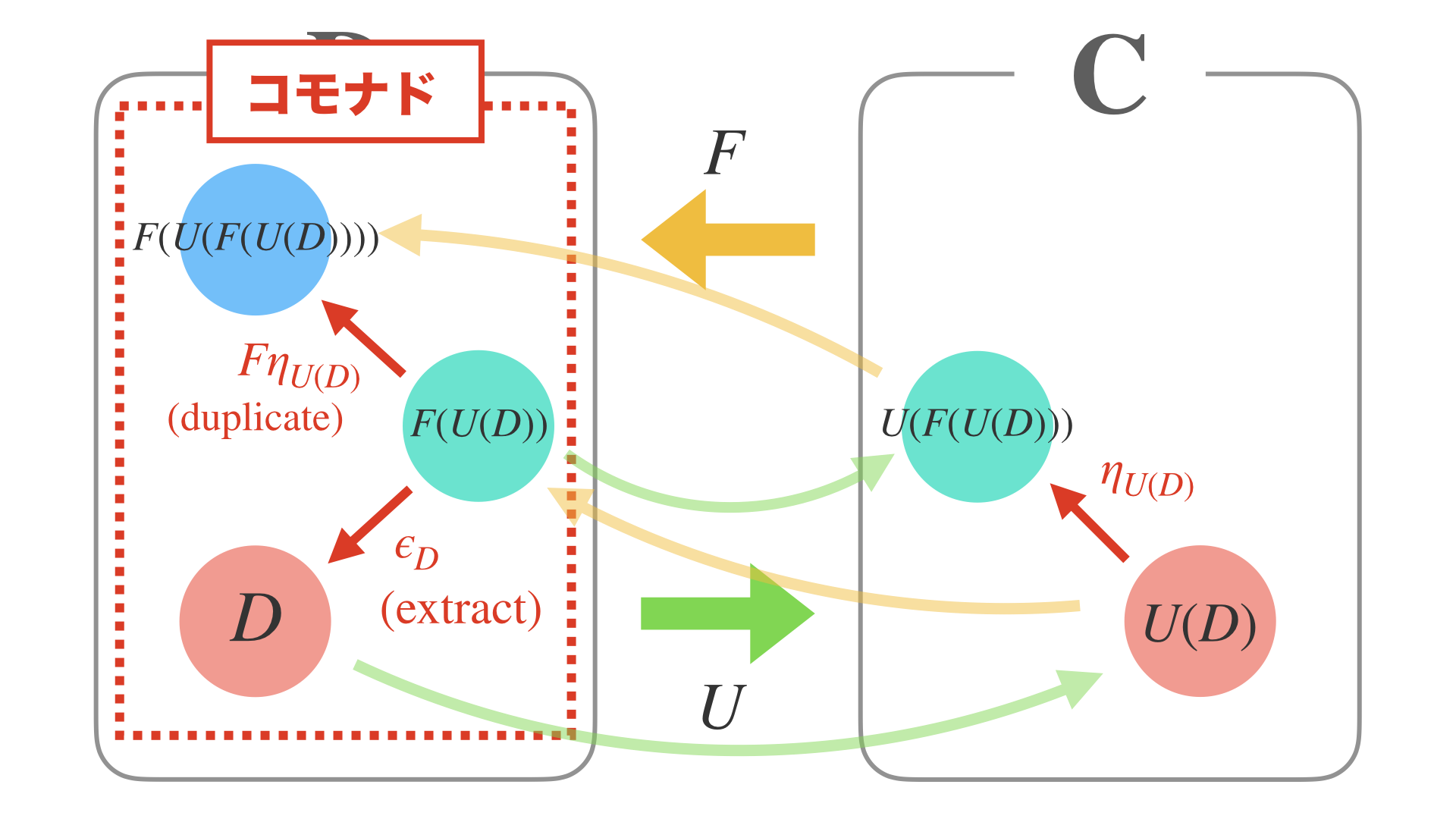
そして先ほどの「直積と冪の随伴」からコモナドを作ると、
いわゆる Storeコモナド が出来上がります。
コモナドの作り方はやはり先ほどと似ていて、今度はモナドの時とは向きが逆で、
右随伴→左随伴の往復を2セットすると出来上がります。
ちなみにコモナドを使った例としては、例えばライフゲームがあります。
ライフゲームというのは、簡単な生存ルールを用いたシミュレーションゲームで、
2次元平面上で、隣のセルの生死に応じて、自分のセルの生死が決まるものです。
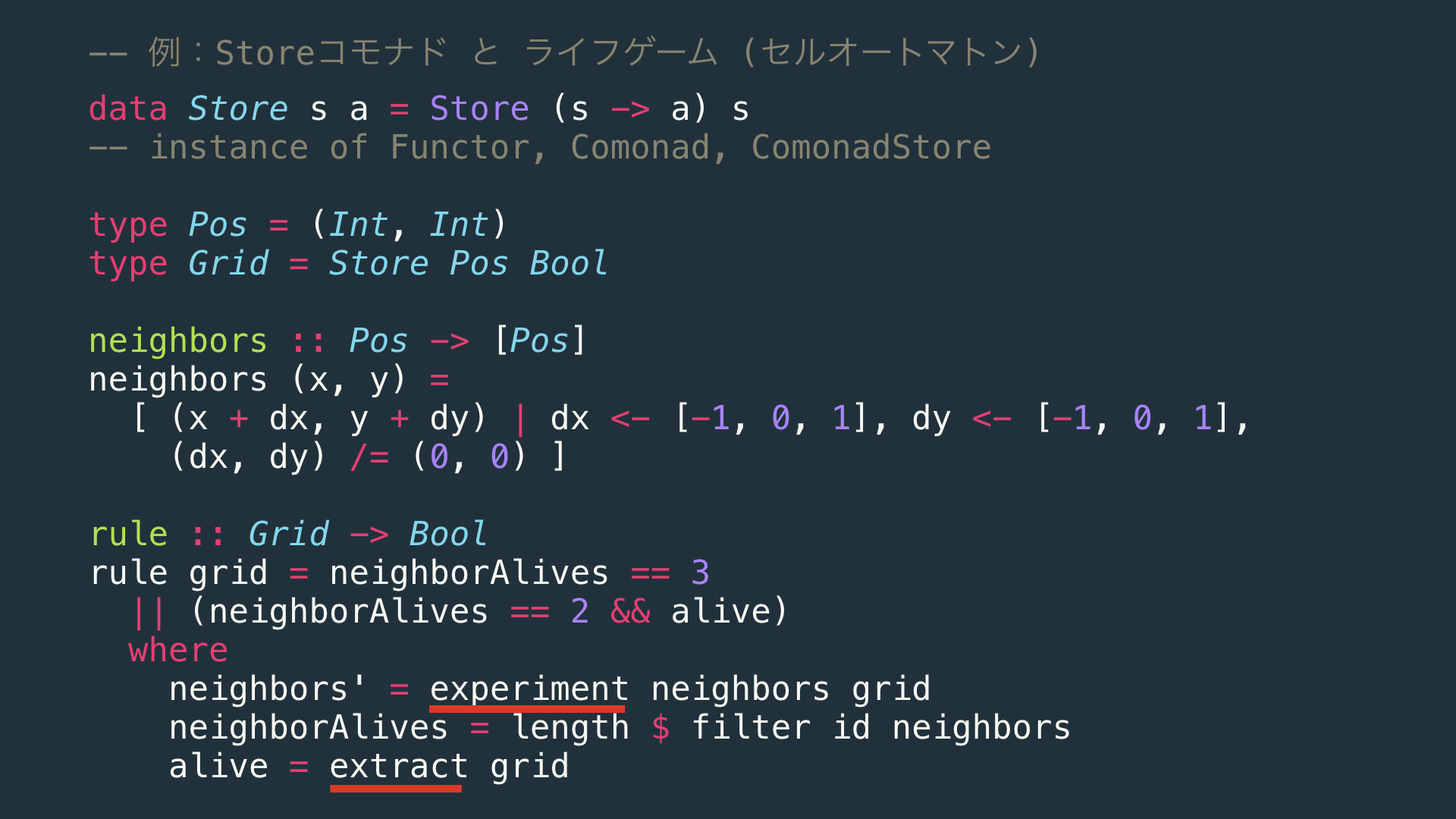
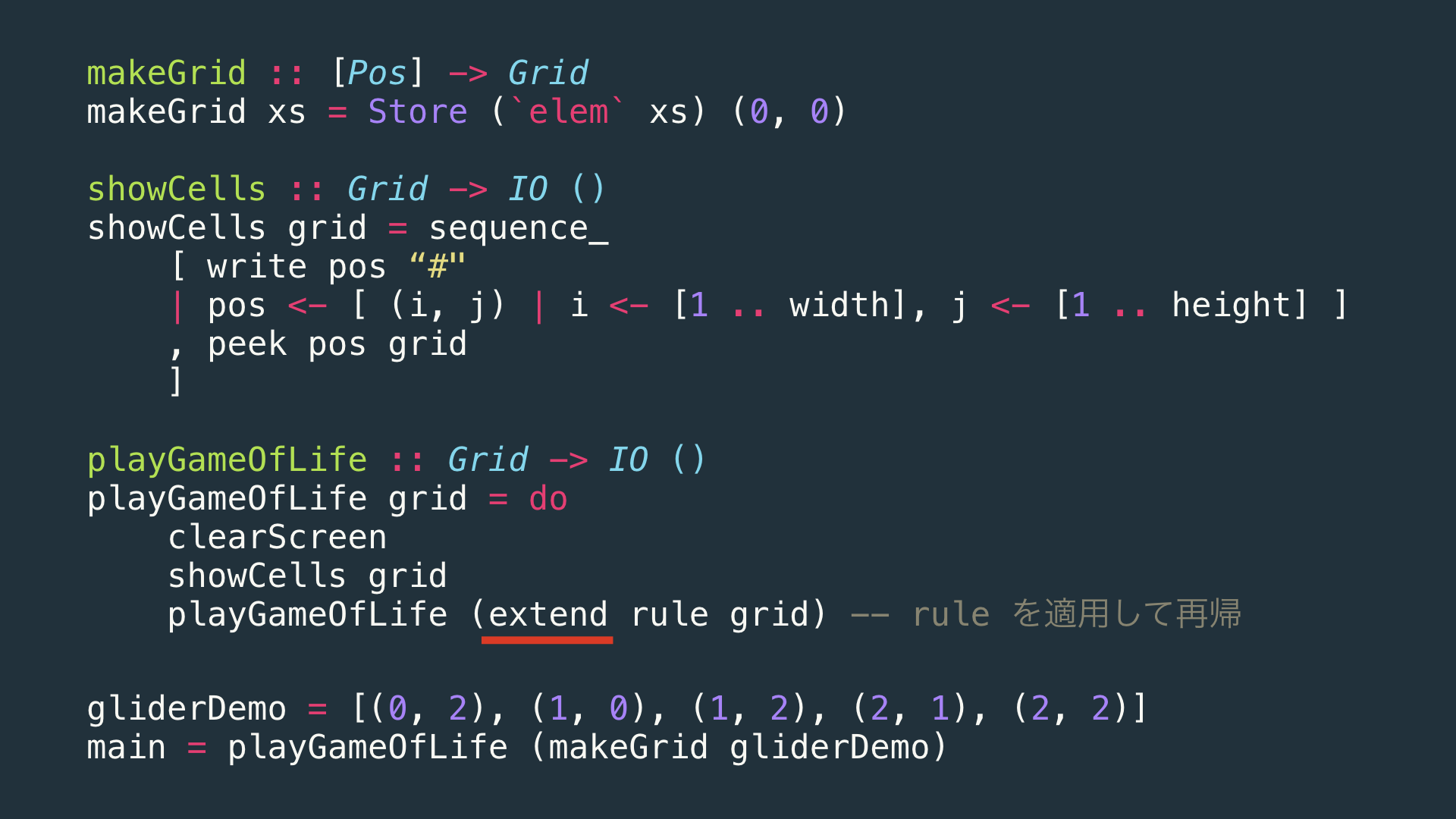
これをHaskellでサクッと実装すると、コモナドの力を使って。。。
たったこれだけのコード量で実装できます。
一応、赤線で引いた箇所がComonadのキモとなる部分です。
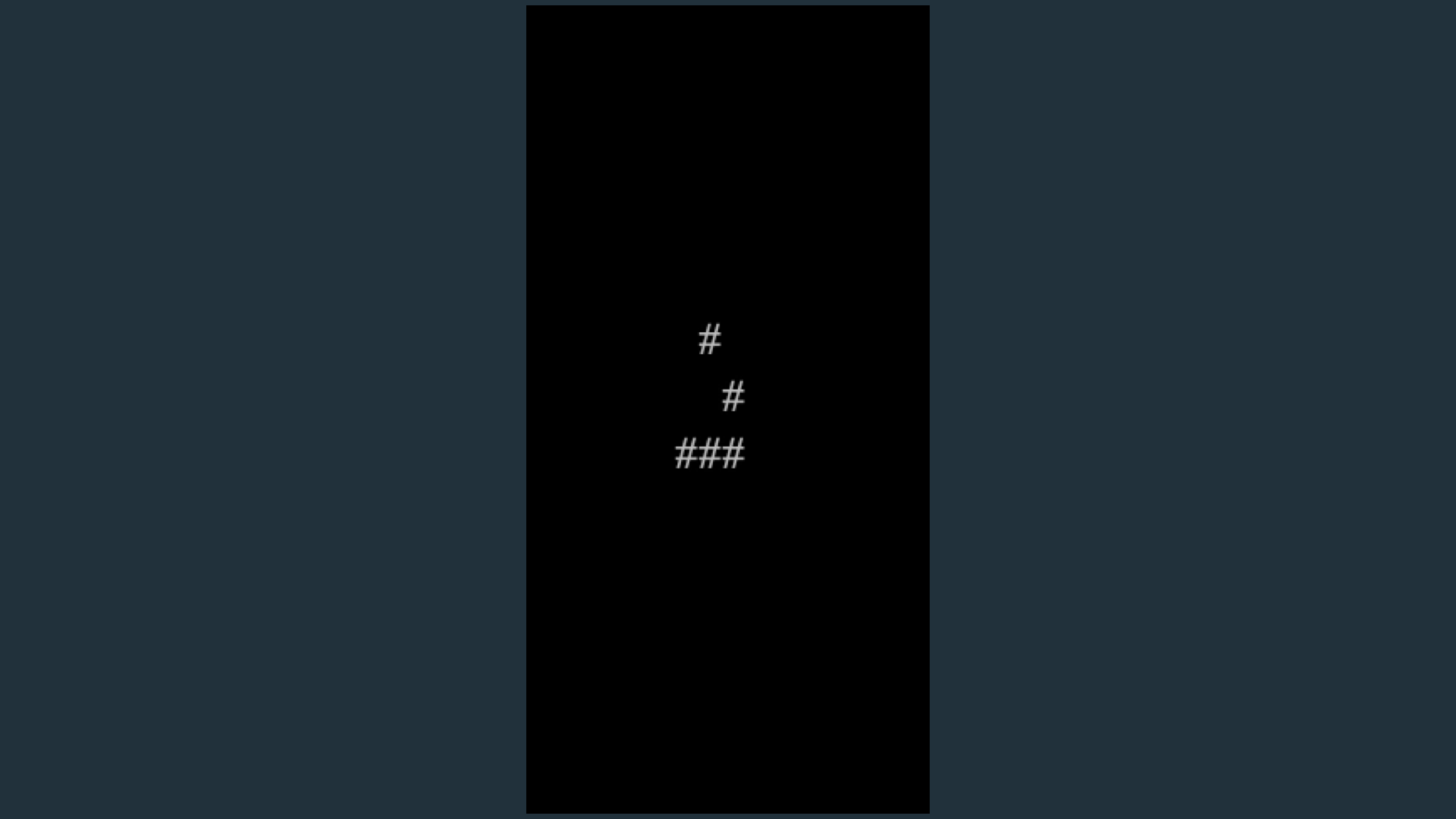
そうすると、例えば簡単なgliderと呼ばれるライフゲームの例がこのように斜めに進んで動きます。
(NOTE: メモ化のない関数を使ったStoreコモナドはパフォーマンスが悪いので注意。実際は、高速な Vector などを使います)
続きまして、アプリカティブ関手の話に移ります。
アプリカティブというのは、HaskellにおいてFunctorとMonadの中間に位置する重要な型クラスで、
例えば並列計算やより高速なパーサー処理などに使われますが、
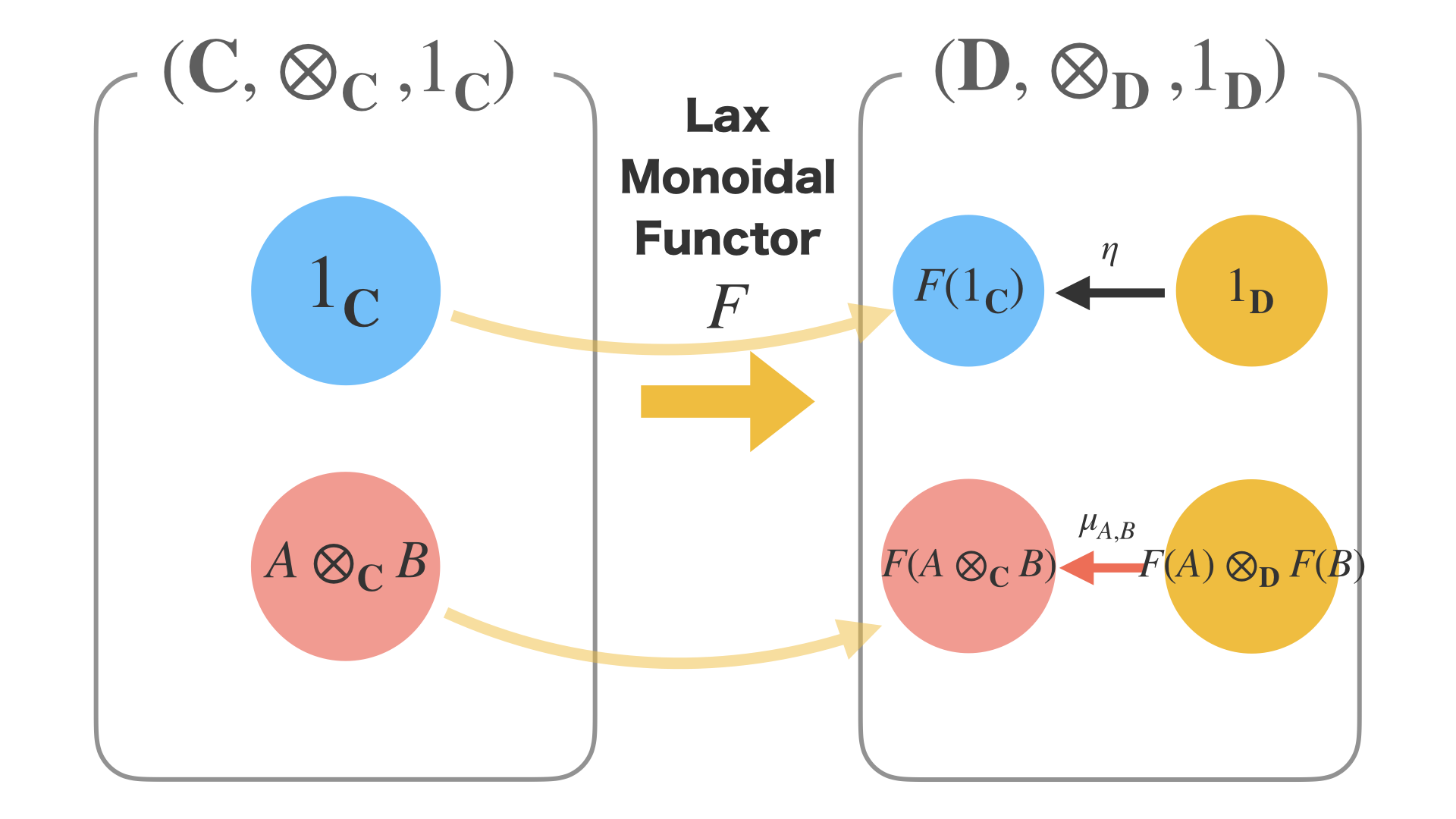
これは圏論でいうLax Monoidal関手というものを使って説明することができます。
Lax Monoidal関手というのは、2つのモノイダル圏の間をマップするFがあり、
さらに、単位対象とモノイド積について、右の圏にあるηという射とμという自然変換が備わっていることを指します。
この2つの矢印は、必ずしも同型射ではないというのがポイントで、**Lax Monoidal(緩いモノイダル関手)**と呼ばれる所以です。
そして、これらのLax Monoidalの性質に、strength というもう一つの自然変換が加わると、
Haskellにおける有名なApplicativeになります。
ここでは、ηとμに着目すると、Haskellでは unitとzipという関数を使って定義することができます。
ちなみに、実際のHaskellのApplicativeは、unit と zipではなく、
下にある pureとliftA2という関数を代わりに実装することを条件としています。
ちなみに unit から pure への変換は、米田の補題を使うと簡単に同じものであることが示せます。
ここで余談として、Day Convolution と呼ばれる「関手の積」があります。
これにもし F == G とおくと、まさにApplicativeと同じ構造が得られることになります。
実は、アプリカティブというのは、モナドと同じく
「自己関手の圏におけるモノイド対象(ただしモノイド積は、Day Convolution)」
であり、これが先ほどの Lax Monoidal関手と等しくなります。
続いて Profunctor/Arrow についてお話しします。
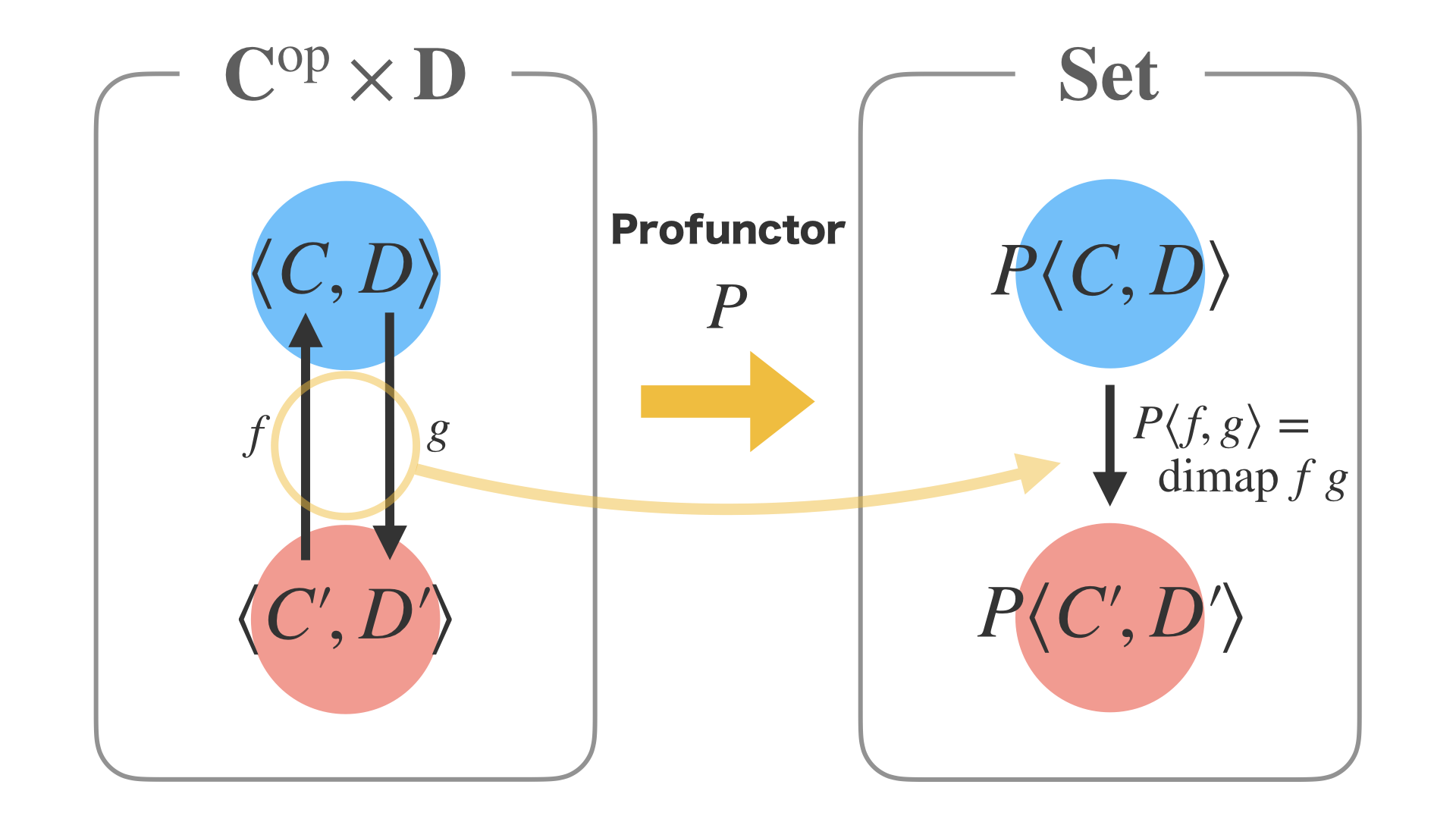
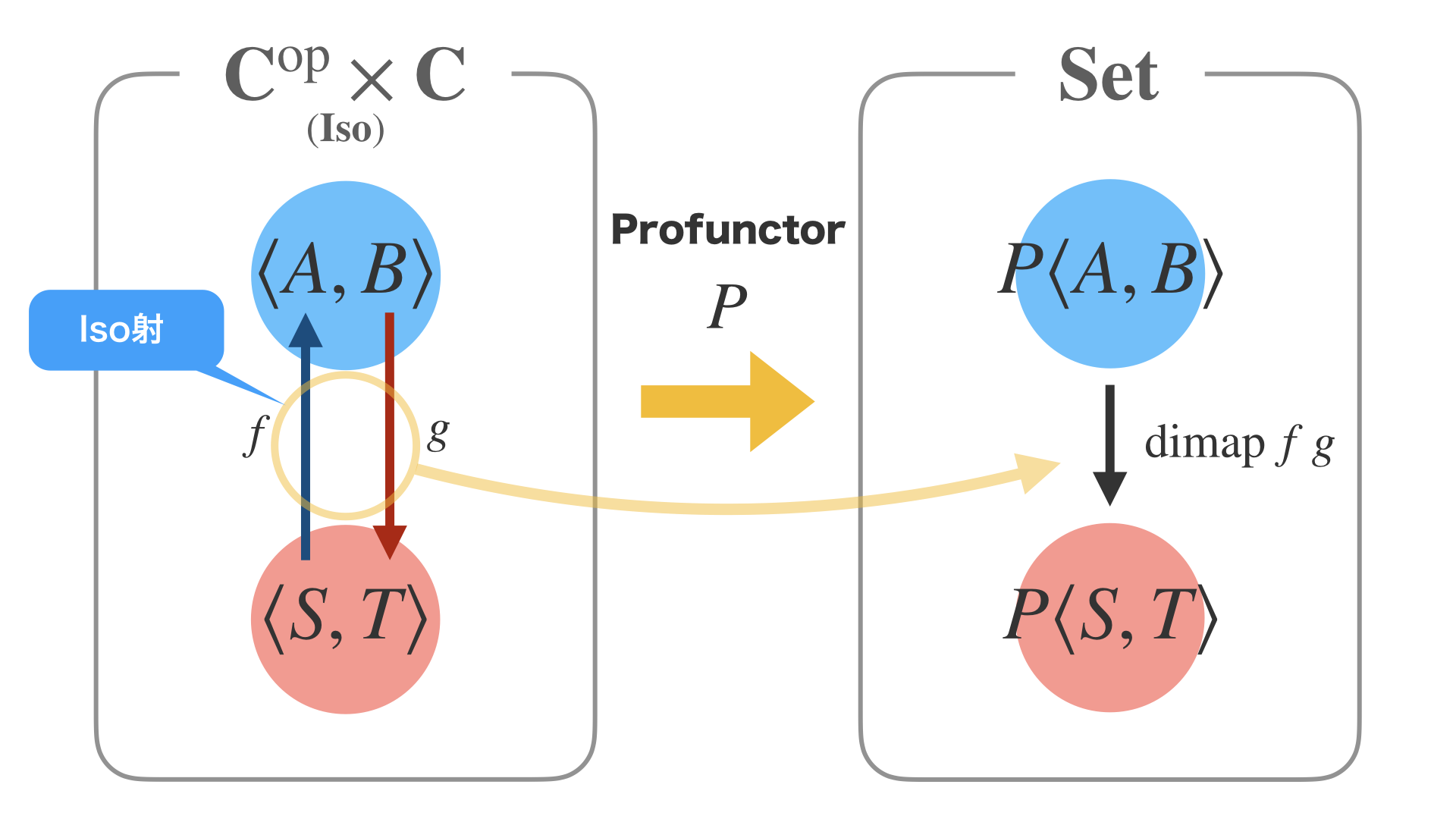
Profunctor というのは、2つの圏CとDに対して、左側のC^opとDの積の圏からSet圏への関手を意味します。
すると、左側で双方向に伸びる射 f と g が、Profunctorによって、dimap f g に写ります。
これをHaskellで書くとこのようなコードになります。
次に、このProfunctorにさらにstrengthという自然変換を追加します。
(NOTE: 先ほどのアプリカティブ関手に備わるstrength の profunctor版)
モノイド積に「直積」ないし「直和」を用いることで、
StrongProfunctor と ChoiceProfunctor をこのように定義できます。
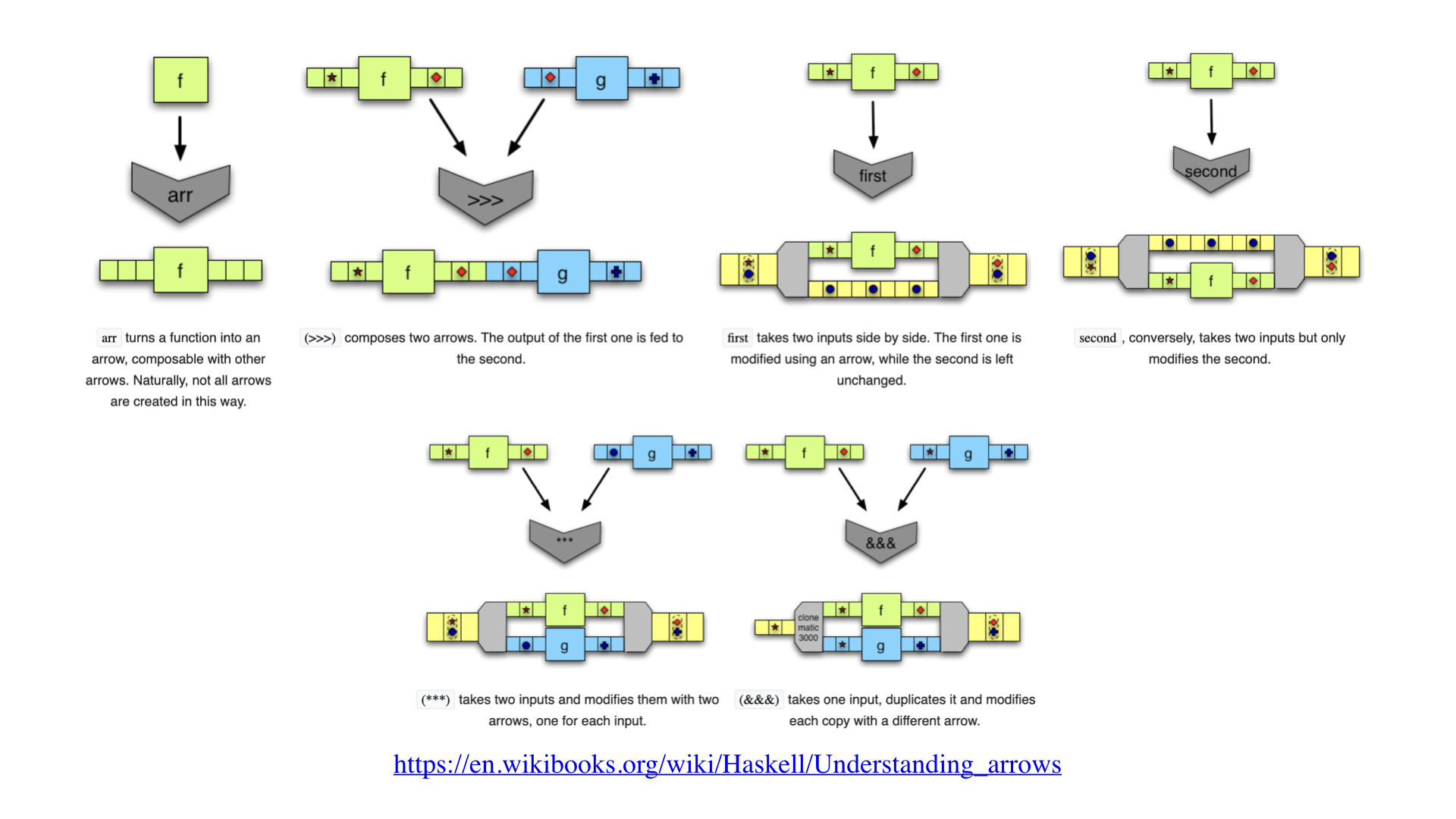
そして、これらにさらにモノイド対象を加えると、Arrow や ArrowChoice と呼ばれる構造になります。
この図は、Arrowの基本的な性質をまとめた図になります。
アプリカティブやモナドと同じく、並列や直列の計算効果を表せる一方で、
Arrowの場合は、入力を受け取って選択できるなど、より抽象度の高いクラスになります。
このArrowを使った例としては、Profunctorと合わせて考えると、
実は圏論でいうところの直積・直和の普遍性について説明することが可能です。
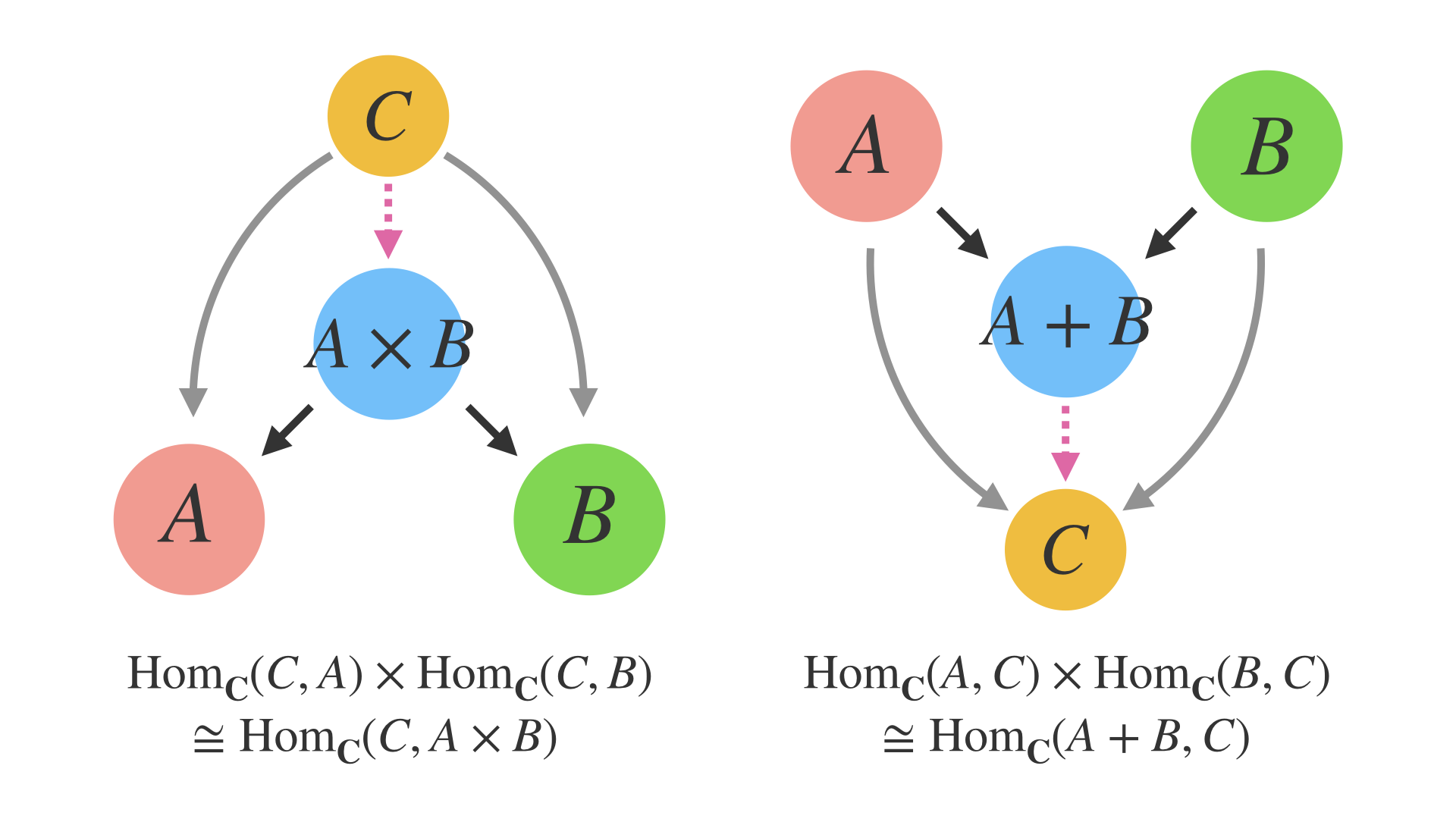
まず、Arrowの (&&&) と Profunctor の unzip から直積の普遍性が得られます。
また、ArrowChoice の (|||) と Profunctor の unzipEither から、直和の普遍性が導かれます。
直積と直和の普遍性を図に表すと、ご覧の通りです。
圏論では当たり前に見るこの図式ですが、プログラミングの世界でいえば
複数の関数を束ねたり、パターンマッチングで分岐したり、プログラミングの重要な側面について説明しています。
そしてそれらを抽象化する考え方がArrowといえます。
それではいよいよ Opticsと呼ばれるLensの一般化について見ていきます。
Lensというのは、複雑なデータ構造のアクセスを提供する型になります。
例えば、この図のようなツリー構造があったとして、その奥底にあるノードの情報を変更したいとします。
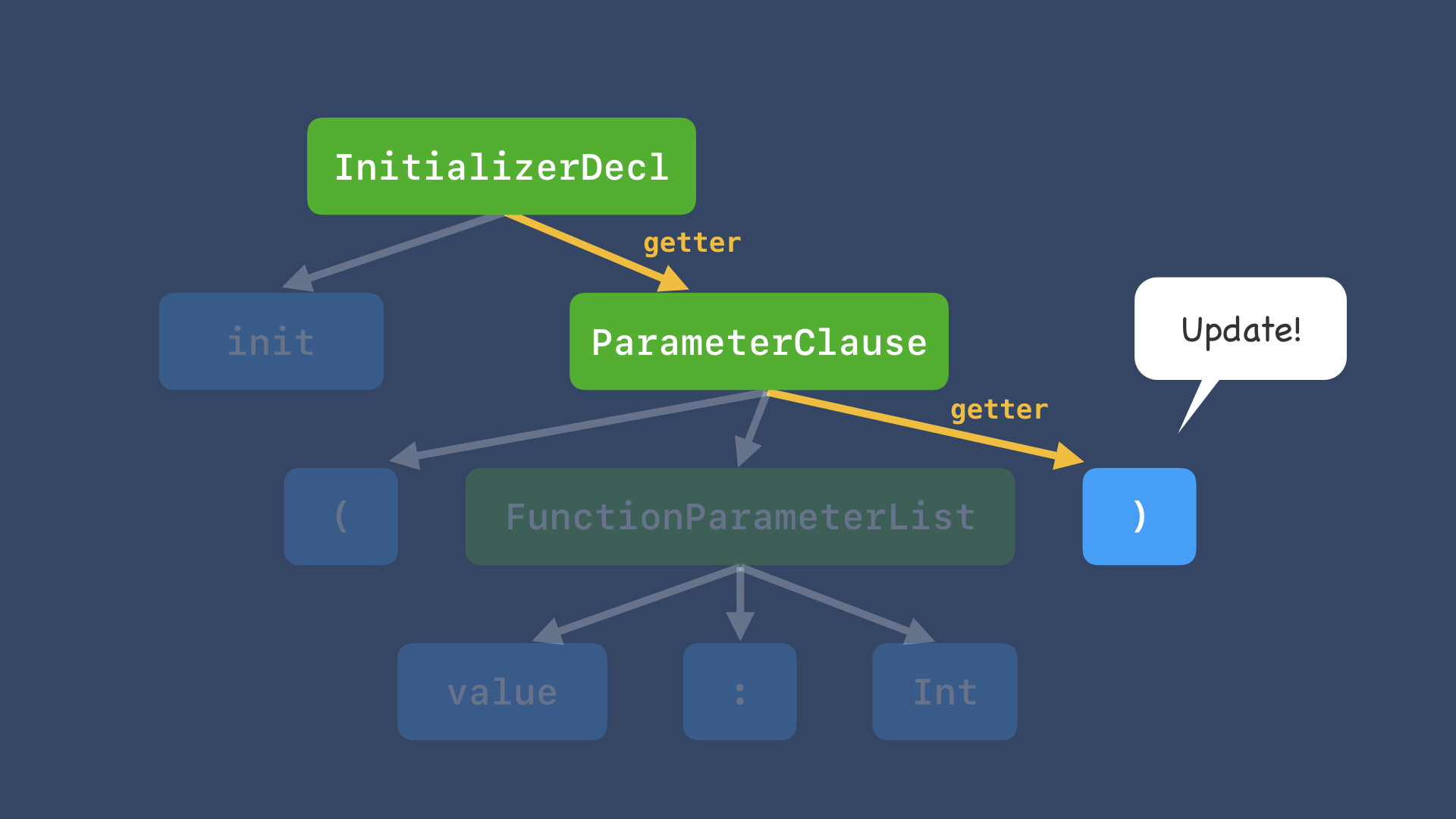
その際、必要なステップとしては、まずゲッターを使って下位のノードにアクセスして。。。
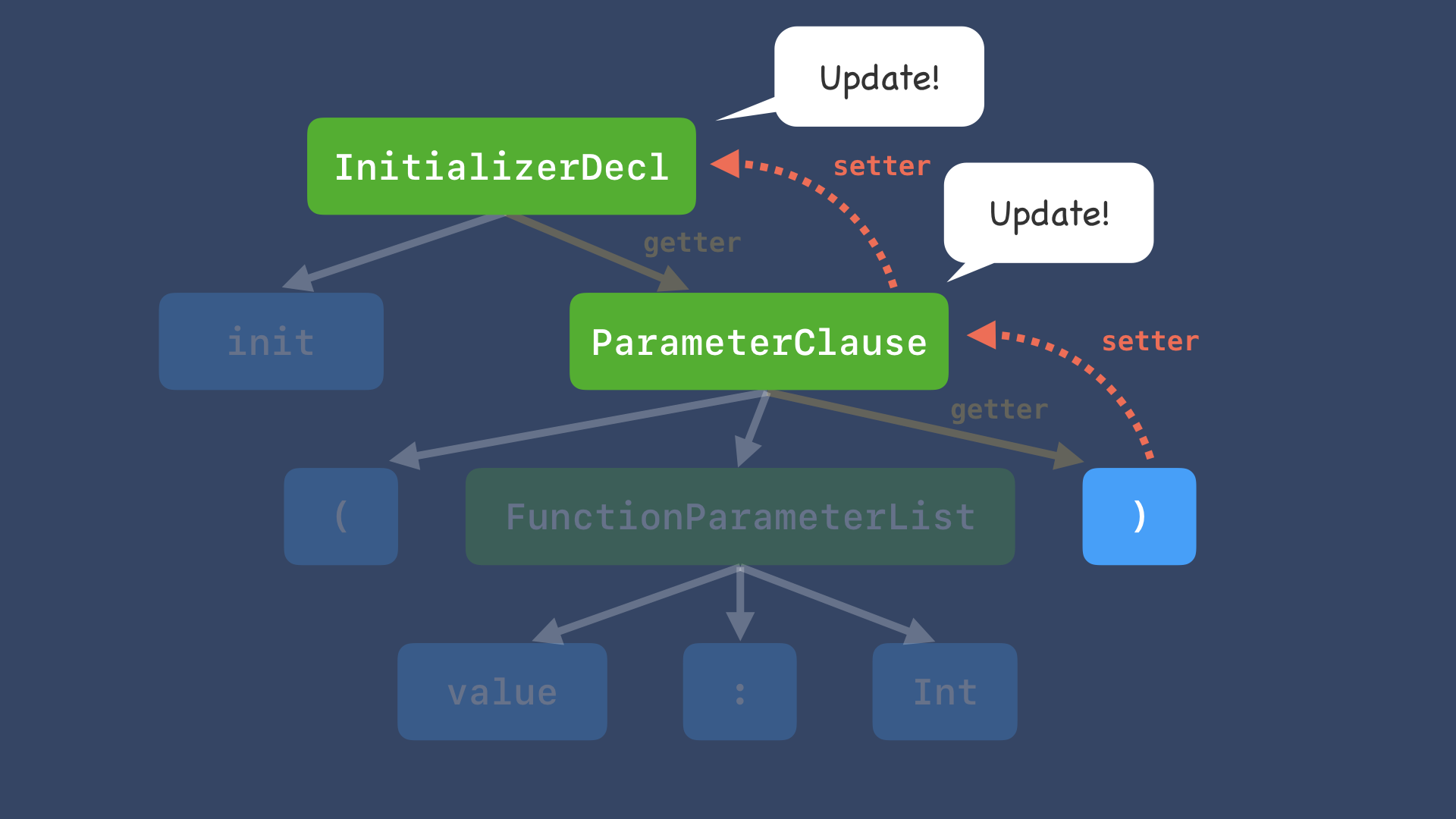
それを更新したら、親ノードを含めて次々にアップデートしていきます。
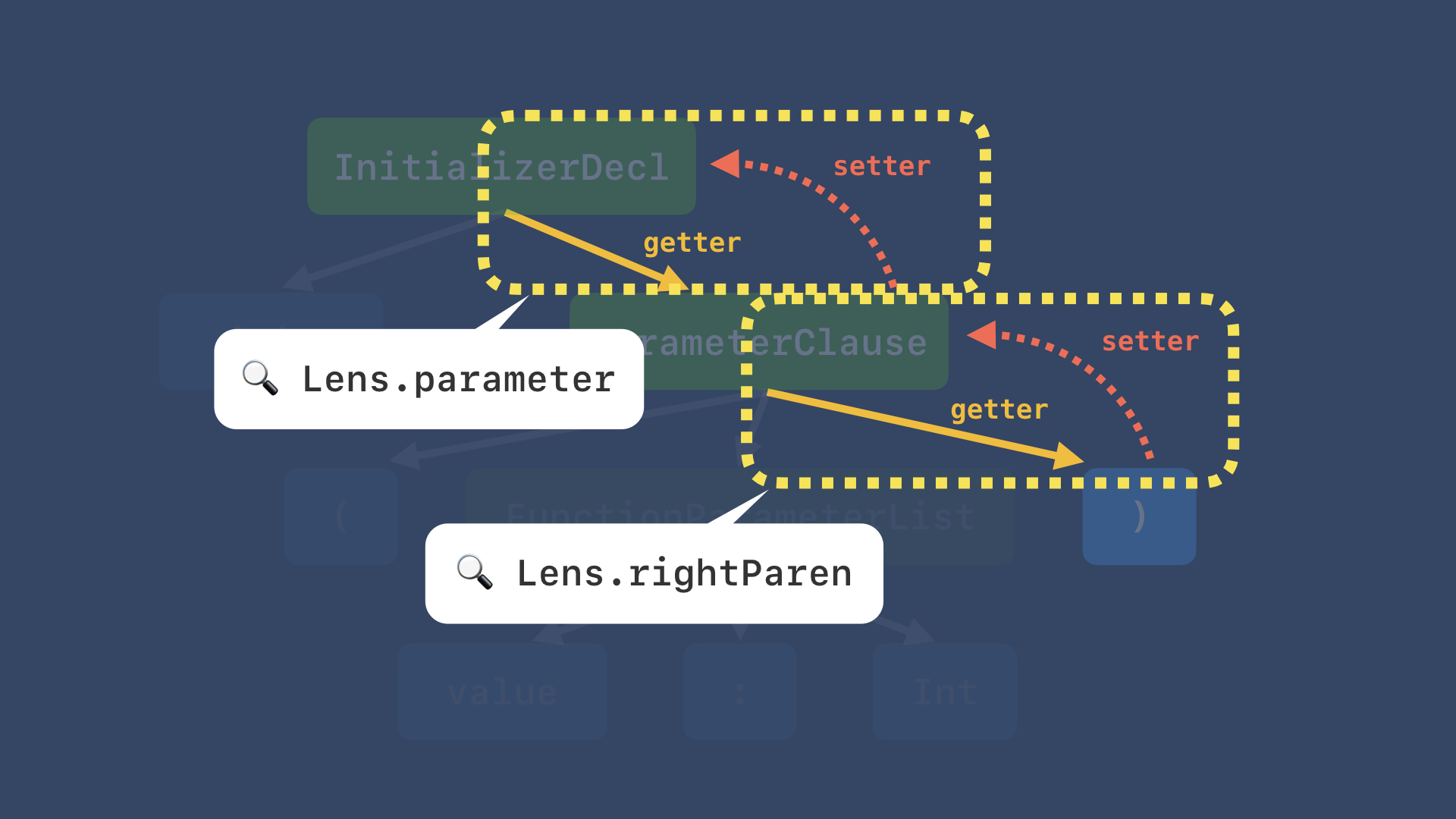
つまり、各階層でゲッターとセッターの両方が使用されて、このペアのことをLensといいます。
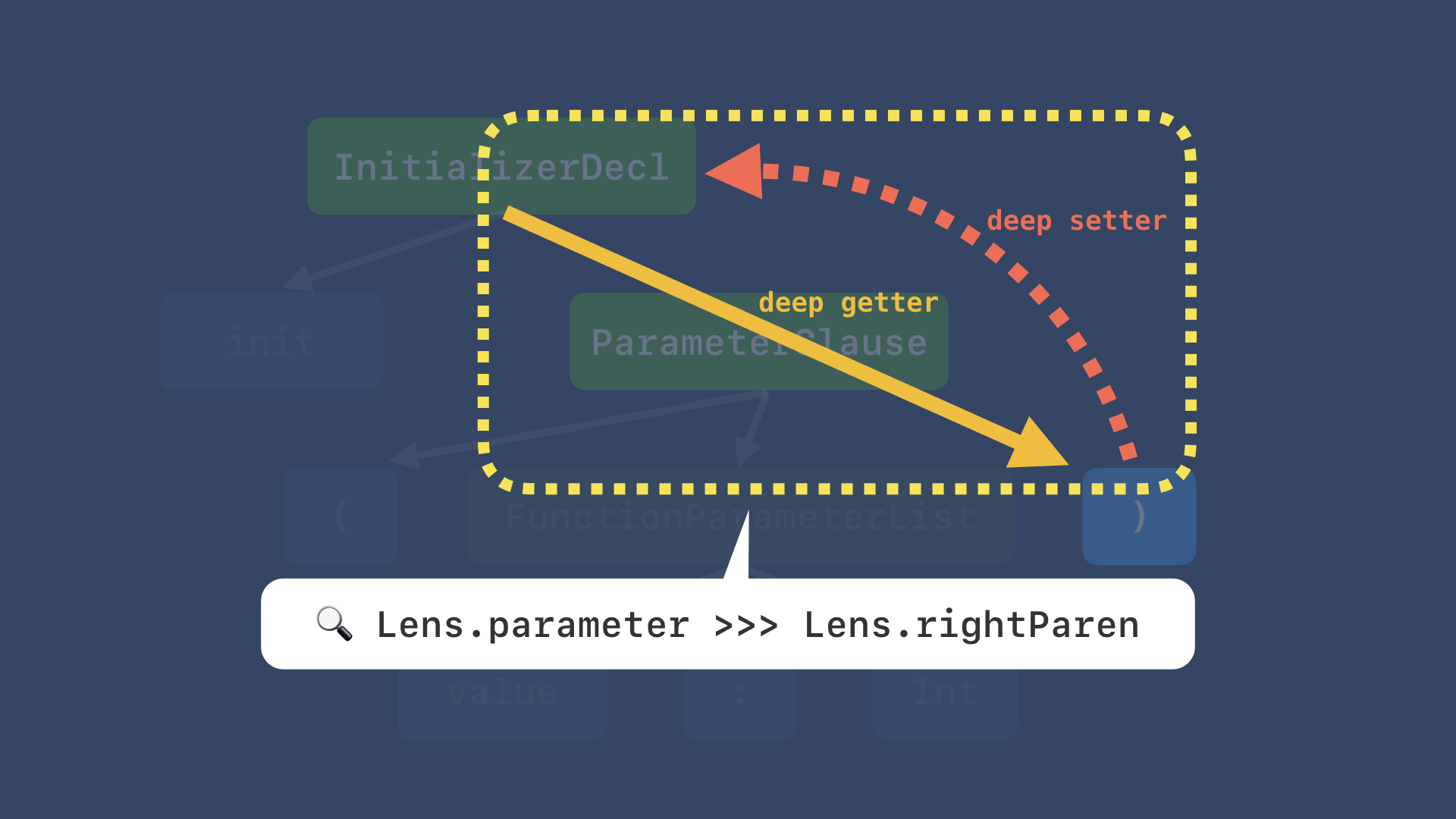
そうすると、最初の例にもあった通り、Lensは圏を構成するので、2つのLensを合成することが可能です。
この図のように、合成して deep な getter と setter のレンズを作ることができます。
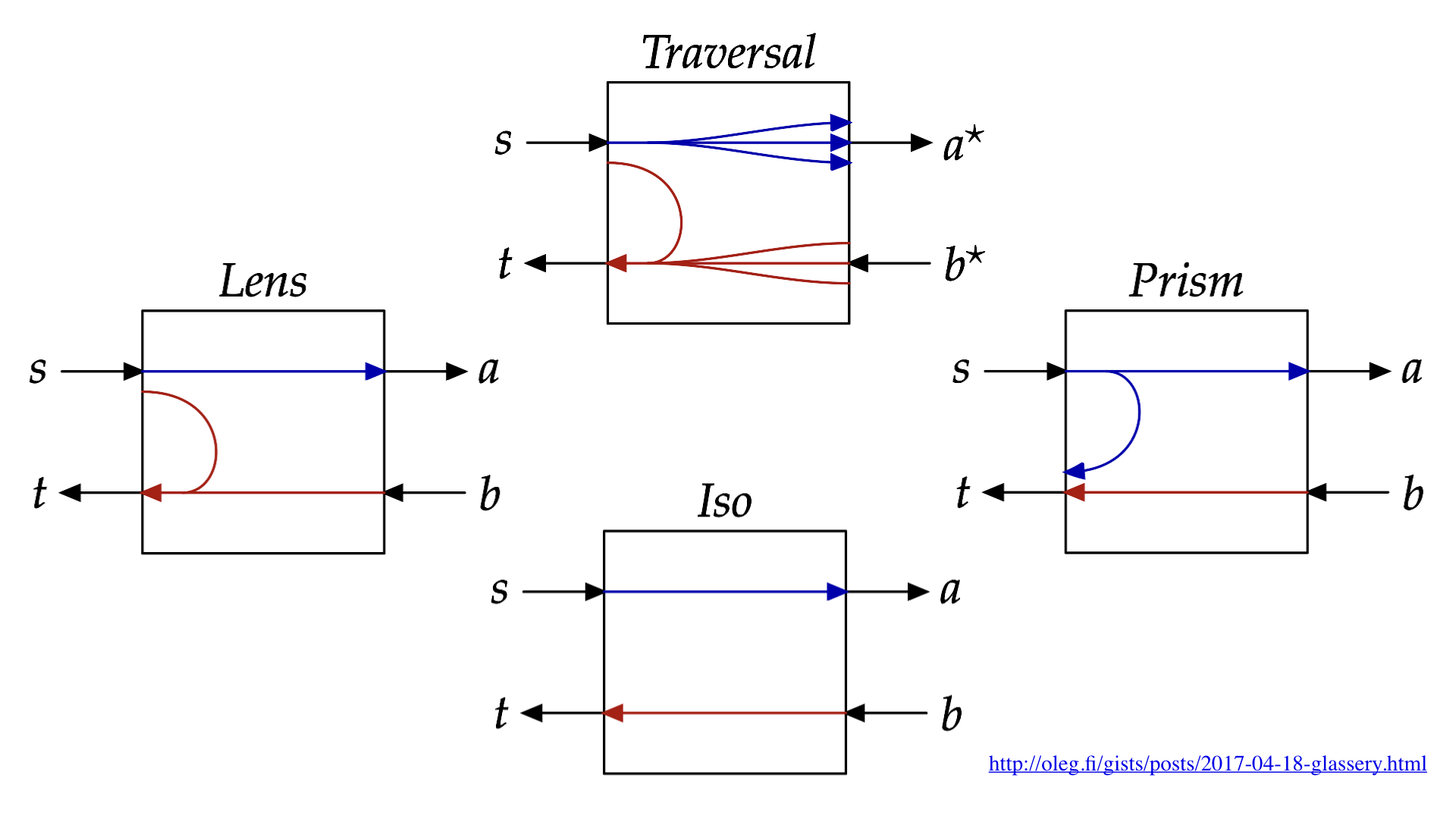
ちなみに、この図の矢印は少し簡略化した書き方をしていて、実際のところは次のスライドのようになります。
つまり左側のLensのように、実際の矢印は単純な双方向ではなく、グニャっとカーブした矢印も含まれているのが分かります。
他にも、PrismやTraversal、Isoなど、様々な形の双方向的な射のペアがあることが分かります。
これらをまとめて**Optics**といいます。
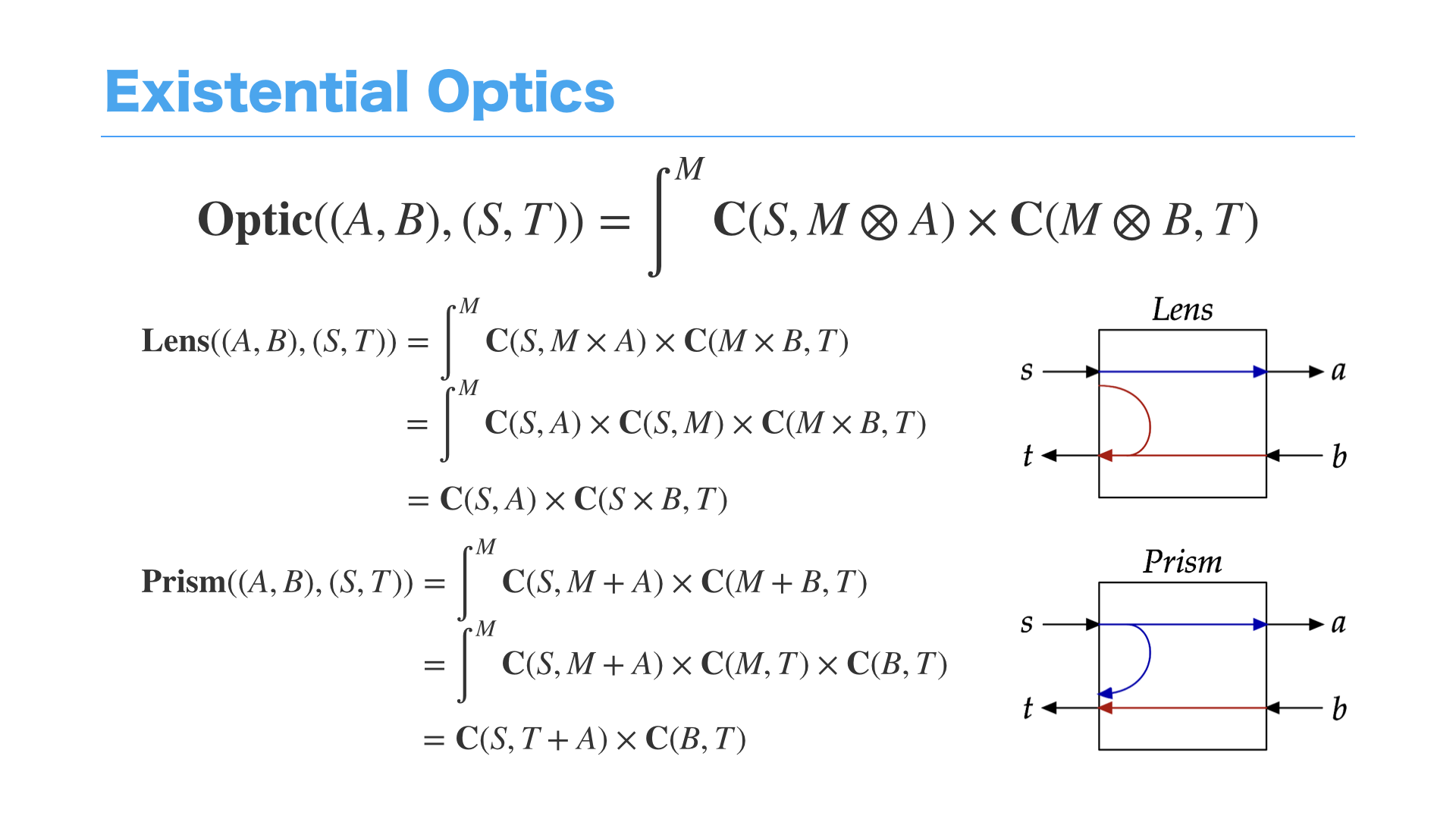
この一連のOpticsパターンを上手く抽象化する方法として、圏論のCoend (存在量化子)を使って上の式のように書くことができます。
そして、テンソル積 ⊗ に直積(タプル)や直和(Either)を代入すると、先ほどのLensやPrismが作れます。
さて、このOpticsパターンですが、もっと上手い書き方はないでしょうか?
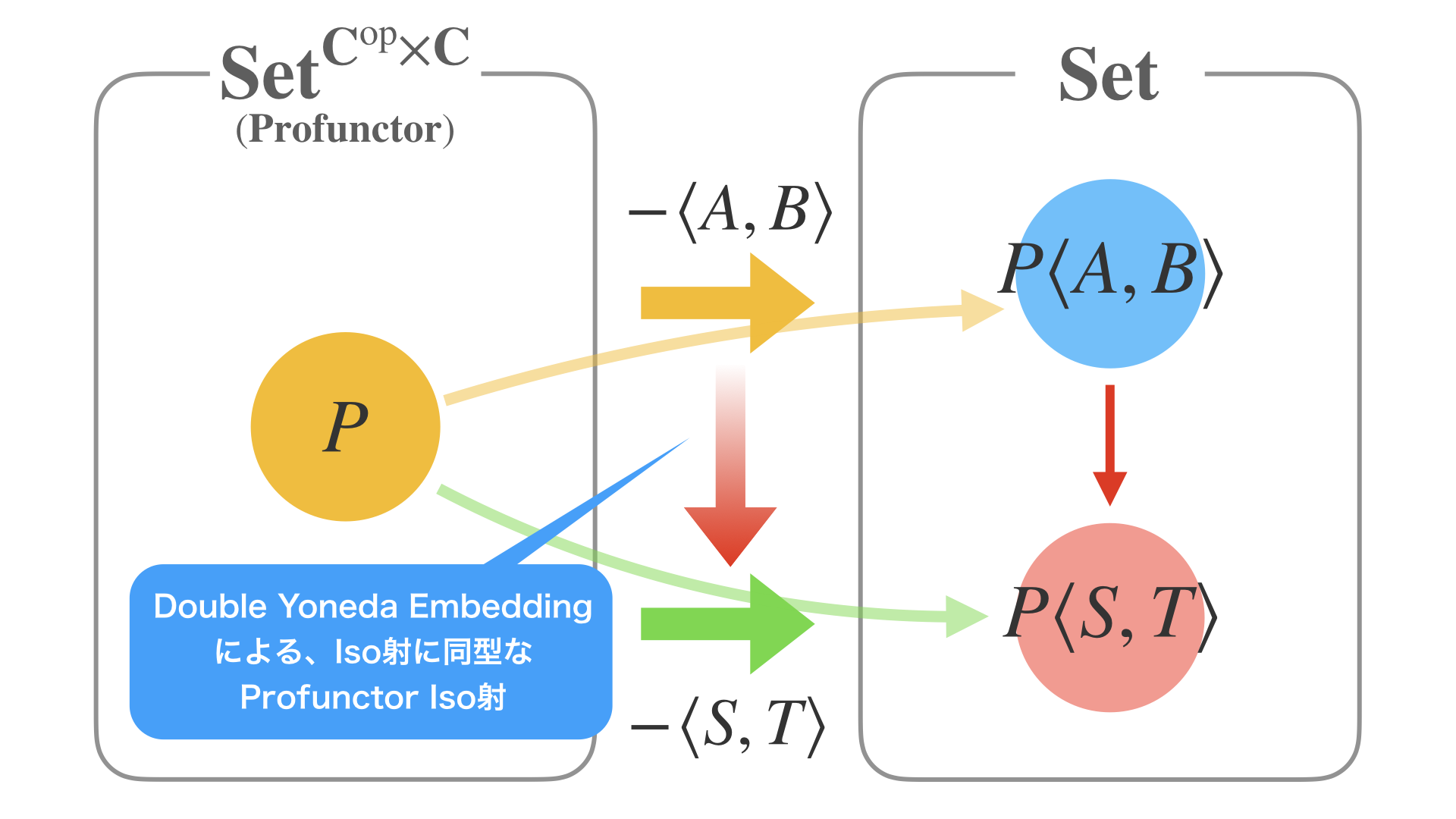
このスライドは、双方向だけからなるIsoの射がProfunctorを経てSet圏に写っている図式ですが、
これは見方を変えると、このようにも言えます。
それは、先ほど中央にあったProfunctorの圏を左側に移行して考えることです。
そうすると、左側にあったIsoの射は、中央の赤矢印の自然変換に対応することが分かります。
これを Profunctor Isoといいます。
この仕組みは簡単で、米田埋め込みを2回行うと、両者が同じものであることが証明できます。
ひとたび、Profunctor Isoが分かると、今度はより複雑なレンズの射を考えたときにも
同じテクニックが利用できて。。。
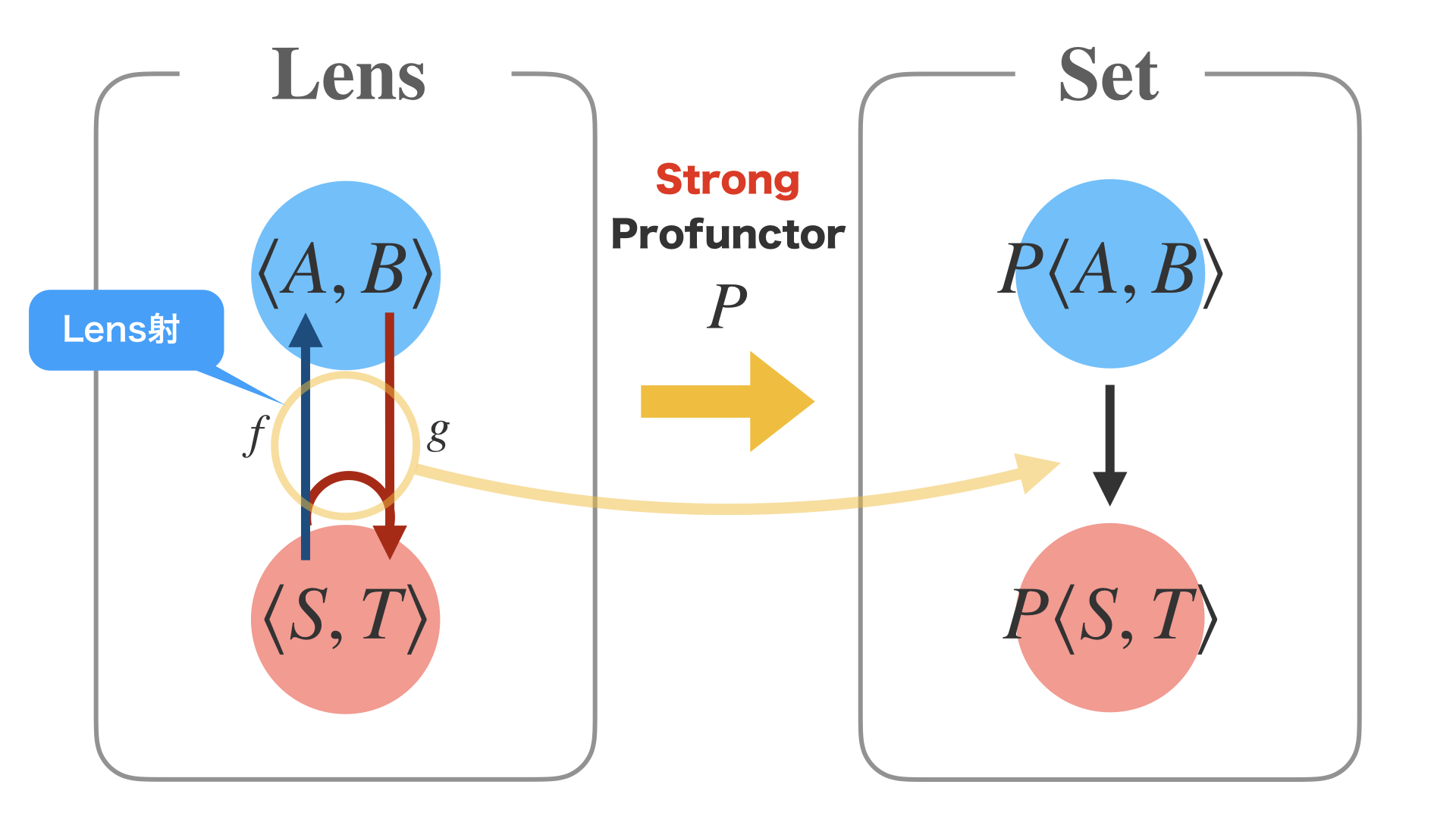
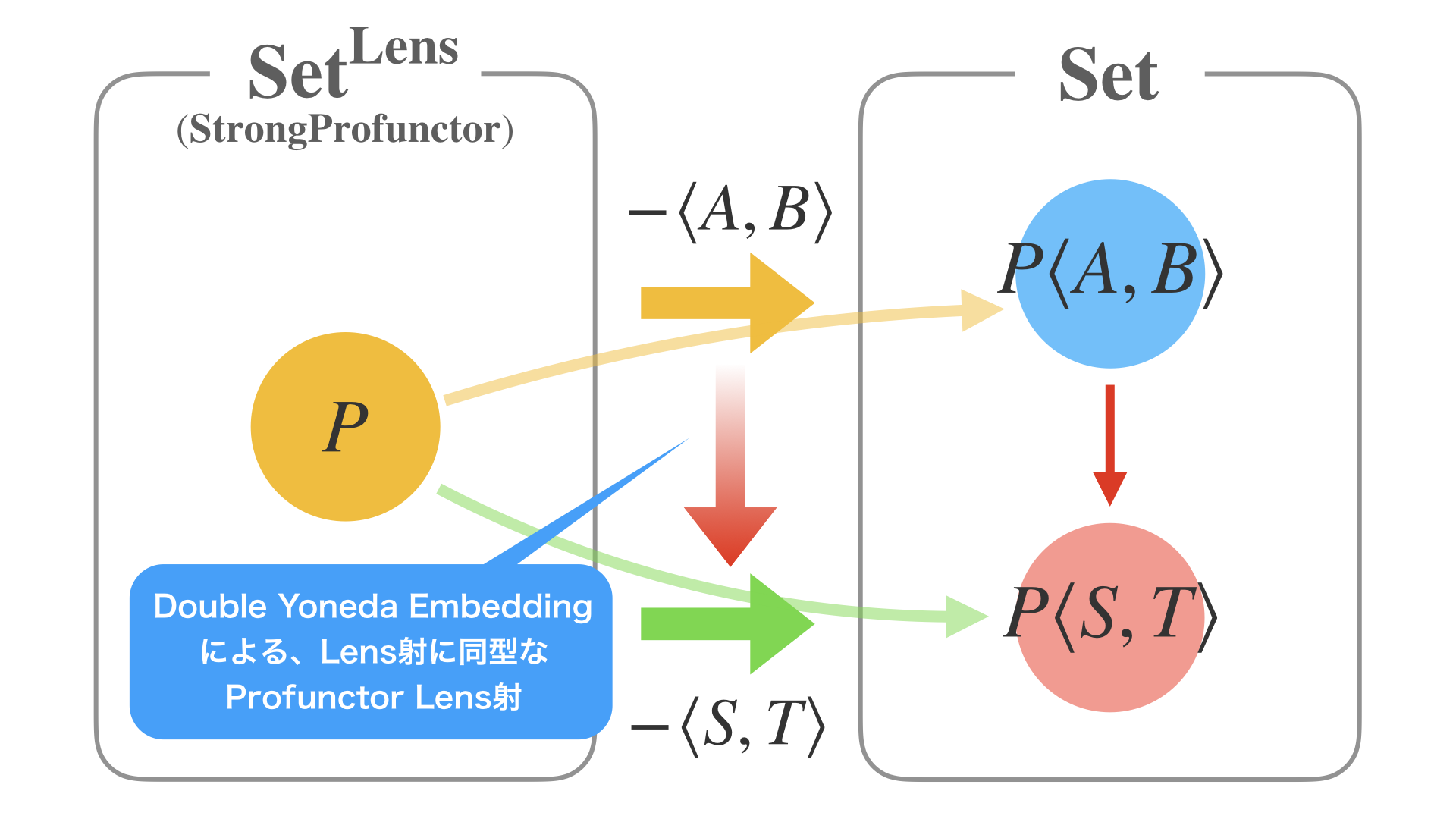
やはりLensも同様に、自然変換を使ったProfunctor Lensの射に置き換えることが可能です。
ちなみに違いとしては、先ほどのIsoではProfunctorを使っていましたが、
Lensの場合はさらに強力なStrongProfunctorを使います。
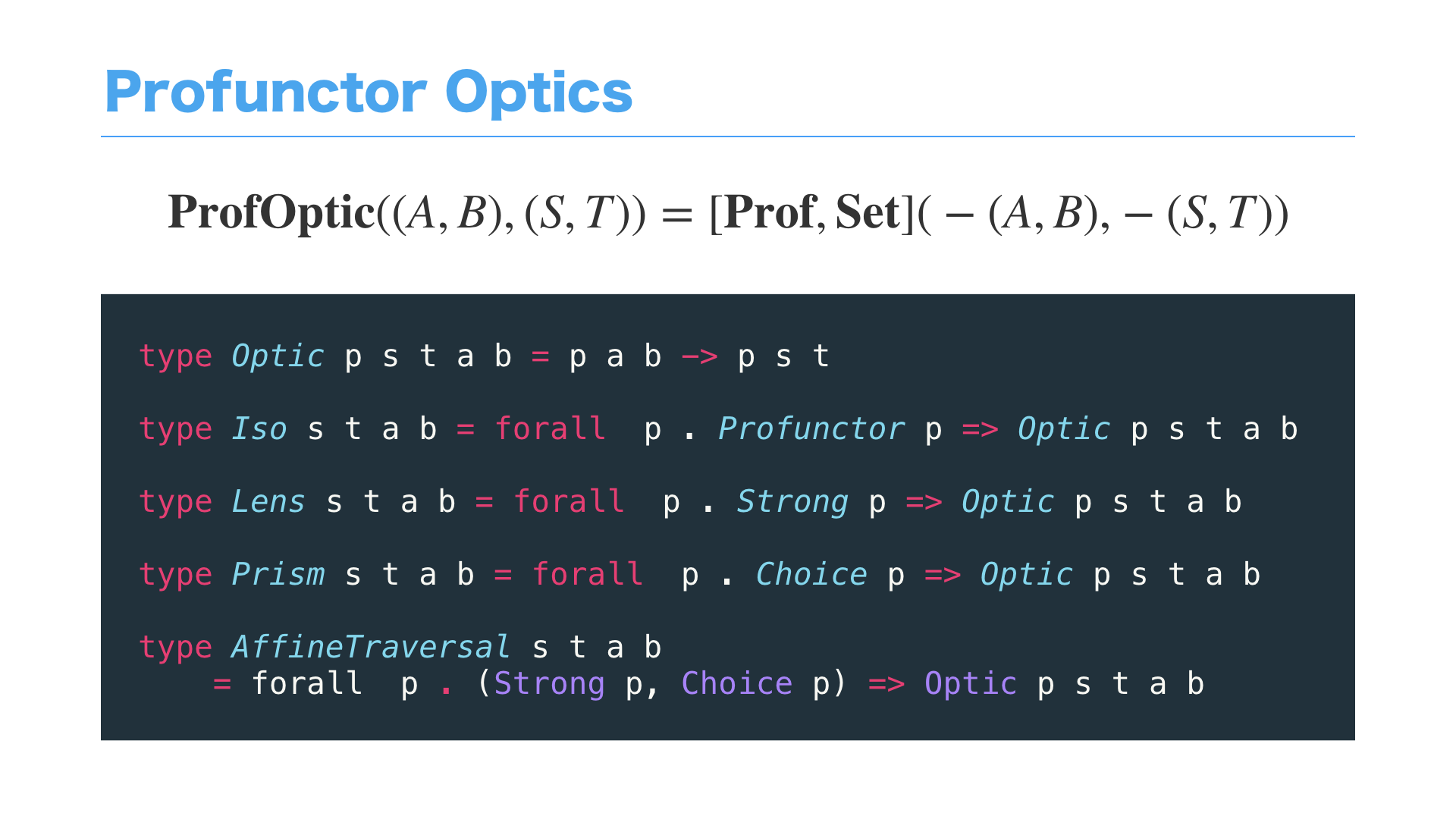
こうすると、Opticsの実装はさらに美しく書くことができて、
突き詰めると Profunctor から Profunctor への自然変換、になります。
ちなみに、Opticsの種類としては、ここにあるのは、あくまで一例で、、、
実際はこの図のように、たくさんのOpticsのパターンとその親子関係で構成されています。
状況に応じて、これらを組み合わせたりしながら、様々なデータ構造にアクセスすることが可能になります。
そして最後に駆け足で、Recursion Schemeについてお話します。
簡単にいうと、再帰的なデータ構造に関する計算全般のことを指します。
再帰的なデータとは、例えばListのような構造で、定義の中で再帰が発生している、つまり右辺の中に左辺が存在するものです。
これは、ListFというベース関手を用意して、その不動点を計算すると求まることが知られています。
Fixの定義から、Fix(F)とF(Fix(F))が同型になり、これを圏論的視点からいろいろ活用できます。
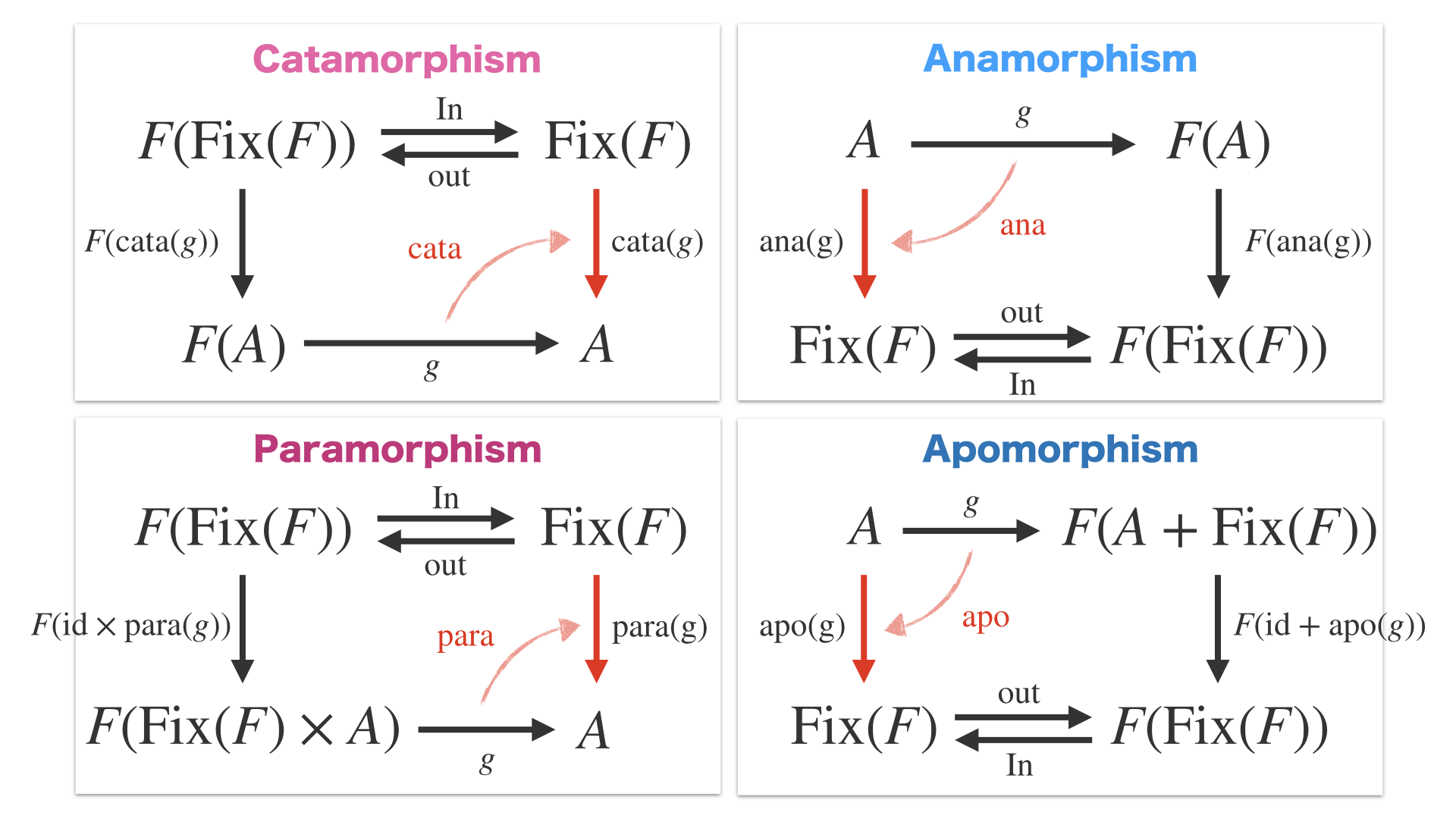
代表的なRecursion Schemeの例としては、
Fixの定義を F-始代数 (initial algebra) として見たときの、そこからの畳込みである Catamorphism であったり、
F-終余代数 (final coalgebra) へのデータ生成となる Anamorphism が挙げられます。
他にも、機能を追加した Paramorphism やその双対の Apomorphism があります。
これらをHaskellで書くとこのように書くことができ、様々な再帰処理の場面で活用することができます。
こちらは先ほどの説明の通りです。
Para-はいわゆる「原始再帰」とも言われます。
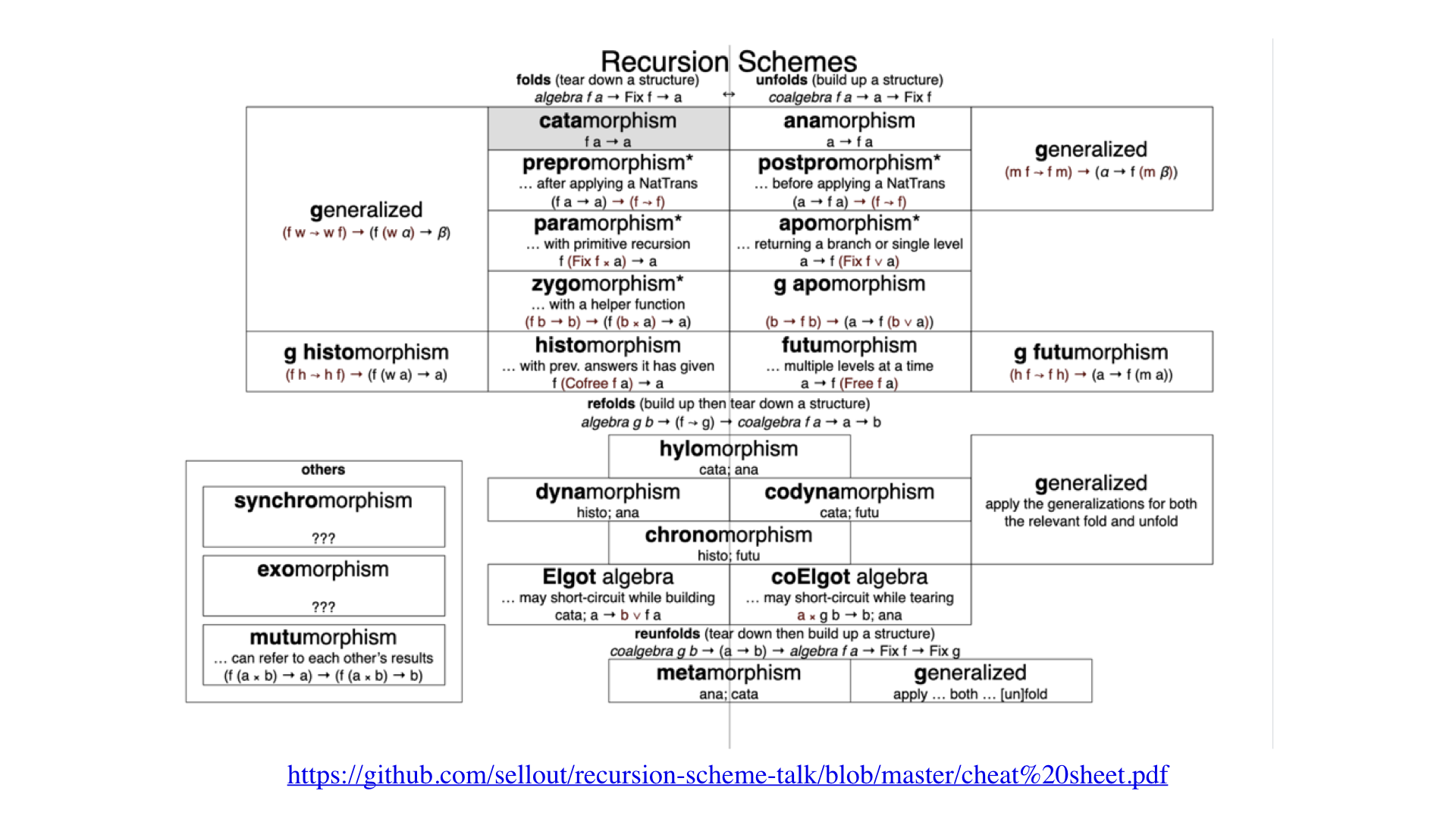
何とかモルフィズムというのは、他にも実にたくさんの種類があり、こちらの図が参考になります。
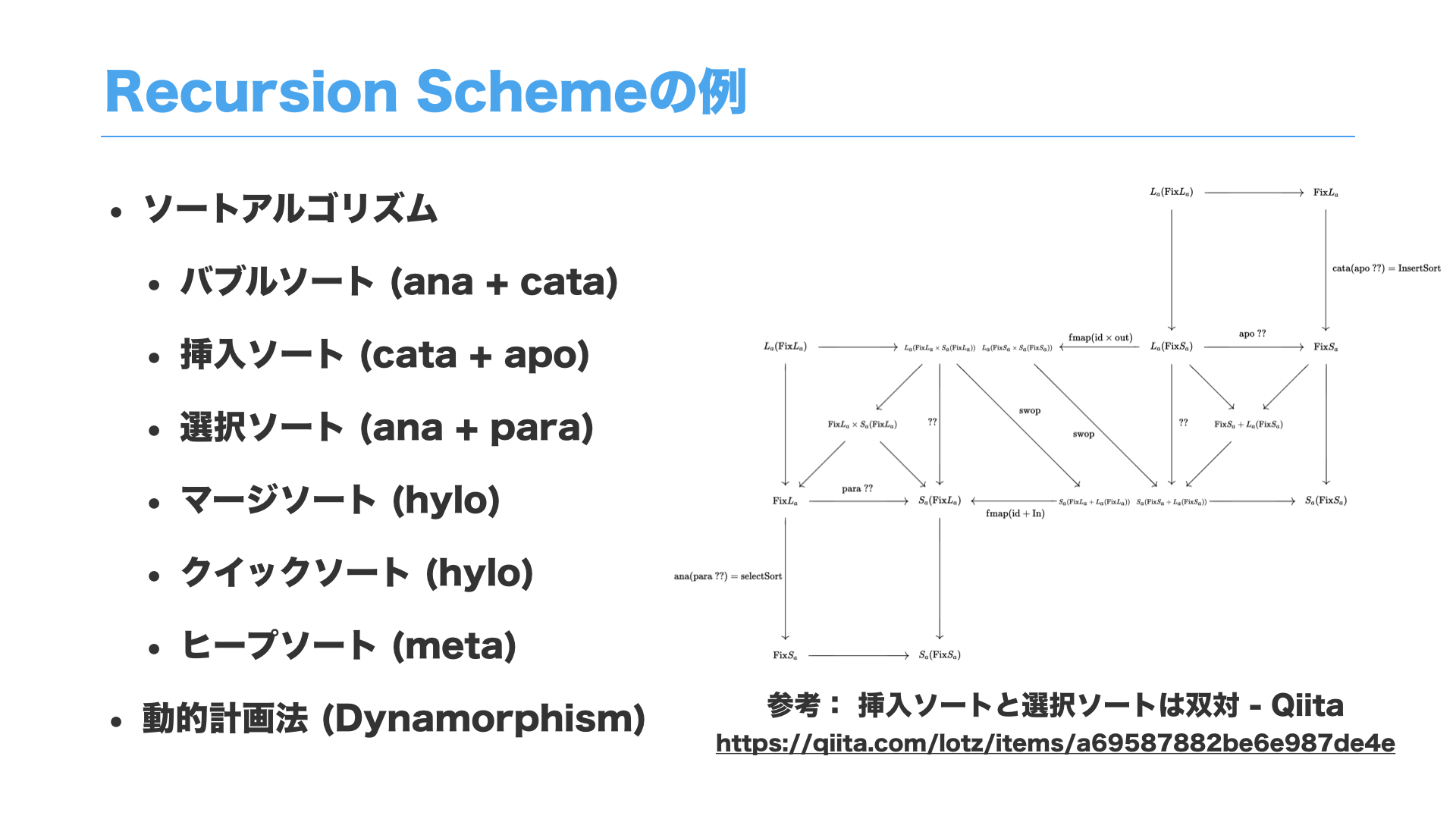
Recursion Schemeは再帰処理のあらゆる場面で活用できます。
例えばソートアルゴリズムや動的計画法などを圏論的視点から眺めると、より面白い結果が見えてきます。
というわけで、以上、駆け足になりましたが、まとめに入ります。
今回、実に様々な圏論の概念について、Haskellでどのように記述できるか、
また、それらがどのように応用されるのかを見てきました。
これらをまとめると、圏論には、プログラミング理論を学ぶためのエッセンスが随所に散りばめられていることが分かります。
個人的な意見としては、圏論は全てのプログラマーには必要ないかもしれませんが、
さらに深くプログラミングそのものを知るためには、Haskellの理解を含め、土台を支える圏論を学ぶことが欠かせないと思っています。
大変駆け足な発表になりましたが、今日の内容から何か皆様の中で得るものがありましたら幸いです。
参考文献:
- Category Theory for Programmers
- 圏論 | 壱大整域
- Monads Made Difficult
- Haskellと随伴 - Qiita
- kan-extensions
- Generalising Monads to Arrows
- Arrows: A General Interface to Computation
- Don't Fear the Profunctor Optics!
- What You Needa Know about Yoneda - Profunctor Optics and the Yoneda Lemma
- Profunctor Optics: Modular Data Accessors
- Categories of Optics
- Functional Programming with Bananas, Lenses, Envelopes and Barbed Wire
- Curse explicit recursion!
- Recursion Schemes - haskell-shoen
- A Duality of Sorts
以上になります。ご清聴ありがとうございました。