先日 Gotanda.hs #1 @HERP というイベントがあって、そこでRecursion Schemesで考える並べ替えアルゴリズムというタイトルでA Duality of Sortsという論文の話をLTしたんですが、この記事ではそこで話せなかった論文の後半で解説されている挿入ソートと選択ソートの双対性について書いていきたいと思っています。
ソートアルゴリズムの復習
まずは主役の二人である挿入ソートと選択ソートについて見ていきましょう。
挿入ソートは与えられたリストの先頭から要素を取り出し、これまでに構築したソート済みのリストに挿入していくという処理を繰り返すことでソートを実現するアルゴリズムです。
 出典: [Insertion sort - Wikipedia](https://en.wikipedia.org/wiki/Insertion_sort)
出典: [Insertion sort - Wikipedia](https://en.wikipedia.org/wiki/Insertion_sort)
これをHaskellで実装すると以下のようになります。
insertSort :: [Int] -> [Int]
insertSort xs = go [] xs
where go ys [] = ys
go ys (x:xs) = go (insert x ys) xs
insert :: Int -> [Int] -> [Int]
insert x ys = xs ++ [x] ++ zs
where (xs, zs) = span (<= x) ys
もう一方の選択ソートは与えられたリストから最小値を選択し先頭に並べ、残りのリストにも同様の処理を繰り返すことでソートを実現するアルゴリズムです。
 出典: [Selection sort - Wikipedia](https://en.wikipedia.org/wiki/Insertion_sort)
出典: [Selection sort - Wikipedia](https://en.wikipedia.org/wiki/Insertion_sort)
これをHaskellで実装すると以下のようになります。
selectSort :: [Int] -> [Int]
selectSort xs = go (select xs)
where go Nothing = []
go (Just (x, xs')) = x : go (select xs')
select :: [Int] -> Maybe (Int, [Int])
select [] = Nothing
select xs = Just (x, xs')
where x = minimum xs
xs = delete x xs
いずれのソートアルゴリズムもgoという関数を使って再帰的に処理を実行するような実装になっていることがわかります。このような再帰関数はアルゴリズムを記述するための強力な道具である一方で、使い方を間違えるとgotoのように必要以上の複雑さを実装に持ち込んでしまう危険性もあります。そのため実装の中にある再帰的な構造(Recursion Scheme)だけを抽象的な関数として切り出すことで、プログラマが再帰的なパターン以外の実装に集中できるようにすることは有用でしょう。例えばGHCで標準的に使えるパッケージbaseが提供するfoldr, unfoldr という関数を使えば先程のソートアルゴリズムは
insertSort = foldr insert []
selectSort = unfoldr select
というふうに実装することができます。実装が再帰的な構造以外の部分insert, selectに集中できているのでとても簡潔に書くことが出来ました。もっと一般的な再帰アルゴリズムを考えるとfoldr, unfoldrだけでは不十分で、より多くの再帰的な構造を表す関数が必要になってきます。これらの再帰的な構造を表す関数を扱う理論が次節で説明するRecursion Schemesなのです。
速習Recursion Schemes
これ以降の話を理解するためにはRecursion Schemesの基本的な事柄について知っておく必要があるので簡単におさらいしておきましょう。
そもそも再帰的な構造がどこから現れるのかを考えると、型それ自体に再帰的な定義が現れていることに気がつきます。例えばHaskellにおけるリストの型定義は
data [] a = [] | a : [a]
と定義されていて、(特殊な構文のおかげで[] a, [a]と見た目は変わっていますが)再帰的にリストの型が定義に現れているのが分かります。
この型を再帰的でない型と再帰的な型に分解してみましょう。
-- | 再帰的でない型
data ListF a r = Nil | Cons a r
deriving Functor -- r について関手になる
-- | 再帰的な型
newtype Fix f = In {out :: f (Fix f)}
-- | これは [a] と同型になる
type List a = Fix (ListF a)
FixとListFを組み合わせたListは実はリスト[a]と同型になることが分かります。すなわち情報を落とすことなくお互いの型の値を行ったり来たりすることが出来るのです。
toList :: List a -> [a]
toList (In Nil) = []
toList (In (Cons x xs)) = x : toList xs
fromList :: [a] -> List a
fromList [] = In Nil
fromList (x:xs) = In (Cons x (fromList xs))
リストをわざわざ2つの方に分けた理由はFixが持つ特殊な性質にあります。Fixはリストという型には依存しておらず、Type -> Typeというカインドを持つ高階型に自分自身を再帰的に適応するというパターンを抜き出した抽象的な型です。実はこのFixが持つ性質を利用するとfoldrやunfoldrのような再帰的なパターンを統一的に議論できる土台を作ることが出来るのです。
Catamorphism
Fixには newtype の定義より In :: f (Fix f) -> Fix f という関数が備わっています。実は f a -> a という関数にはf代数という名前がついていて、Fix f は任意のf代数f a -> aを持ってくるとFix f -> aという関数を作ることが出来るという性質を持っています。このf代数からFix f -> aへの対応付けのことをCatamorphismと呼びます。ここでの登場人物を図に書くと以下のような可換図式になります。

Inとは逆向きのout :: Fix f -> f (Fix f)という関数があるので、可換図式をFix fからaまで左側をぐるっと経由することによってcataを実装することが出来ます。
cata :: Functor f => (f a -> a) -> Fix f -> a
cata g = g . fmap (cata g) . out
具体的にFix ListFにおけるcataの挙動を見てみましょう。例えば先程実装したtoList :: List a -> [a]という関数はcataを使うと
toList :: List a -> [a]
toList = cata $ \case
Nil -> []
(Cons x xs) -> x : xs
と書くことが出来ます。実は foldr :: (a -> b -> b) -> b -> [a] -> b における (a -> b -> b) に対応する部分を Cons の場合の処理で、 第二引数である b に対応する部分を Nil の場合の処理で与えてやっていると考えると、Listにおけるcataはまさにfoldrと対応するのです。そういう意味ではCatamorphismはリストにおけるfoldrの一般化であるとも考えることが出来ます。
Anamorphism
Fixには newtype の定義より out :: Fix f -> f(Fix f) という関数が備わっています。実は a -> f a という関数にはf余代数という名前がついていて、Fix f は任意のf余代数a -> f aを持ってくるとa -> Fix fという関数を作ることが出来るという性質を持っています。このf余代数からa -> Fix fへの対応付けのことをAnamorphismと呼びます。ここでの登場人物を図に書くと以下のような可換図式になります。

outとは逆向きのIn :: f (Fix f) -> Fix fという関数があるので、可換図式をaからFix fまで左側をぐるっと経由することによってanaを実装することが出来ます。
ana :: Functor f => (a -> f a) -> a -> Fix f
ana g = In . fmap (ana g) . g
具体的にFix ListFにおけるanaの挙動を見てみましょう。例えば先程実装したfromList :: [a] -> List aという関数はanaを使うと
fromList :: [a] -> List a
fromList = ana $ \case
[] -> Nil
(x:xs) -> Cons x xs
と書くことが出来ます。実は unfoldr :: (b -> Maybe (a, b)) -> b -> [a] における第一引数である関数の返り値はNothingもしくはJust (a, b)ですがこれらがNilとCons x xsに対応していると考えると、Listにおけるanaはまさにunfoldrと対応するのです。そういう意味ではAnamorphismはリストにおけるunfoldrの一般化であるとも考えることが出来ます。
ところで、ここまでのAnamorphismの説明は先程のCatamorphismの説明とほとんど同じ構造になっていることに気づきましたでしょうか?特に可換図式を見てみると型の位置は変わらずに関数の向きだけが変わっていることに気がつくと思います。実はこのような関係にある2つの概念を双対の関係にあると呼んだりします。これは詳しく説明すると圏論由来の概念で、他にも有名な例としてはタプル(a, b)とEither a bが双対の関係にあったりします1。
Paramorphism
全ての再帰的な関数をfoldrとunfoldrで実装できるわけではありません。ParamorphismはCatamorphismでは直接扱うことが出来なかった再帰的なパターンを扱うことが出来るRecursion Schemesです2。例えばtailsという関数をListのCatamorphismで実装することを考えてみましょう。
> tails [1,2,3]
[[1,2,3],[2,3],[3],[]]
やってみるとすぐに気が付きますが、Catamorphismは再帰のその時点における値全体を扱うことが出来ないのでtailsを実装することは難しいです。そこでその時点における値全体も再帰的なパターンの中で参照できるようにしたのがParamorphismです。

Catamorphismの時と同様に可換図式の一番外を反時計回りにぐるっと辿るとparaが実装できます。
para :: Functor f => (f (Fix f, a) -> a) -> Fix f -> a
para g = g . fmap (id &&& para g) . out
ここで&&&はControl.Arrowで提供されている
(&&&) :: (a -> b) -> (a -> c) -> a -> (b, c)
おおよそ上記のような型の演算子です。
早速paraを使って tails を実装してみましょう。まずはList aに関する便利な関数をいくつか用意しておきます。
nil :: List a
nil = In Nil
cons :: a -> List a -> List a
cons x xs = In (Cons x xs)
これらを使ってtailsは以下のように作ることが出来ます。
tails :: List a -> List (List a)
tails = para $ \case
Nil -> cons nil nil
Cons x (ys, xs) -> cons (cons x ys) xs
実際に Data.List の tails と同じ挙動になっているかどうか確認してみましょう。
> fmap toList . toList . tails . fromList $ [1,2,3]
[[1,2,3],[2,3],[3],[]]
うまく動いてそうですね ![]()
Apomorphism
Catamorphismの双対としてAnamorphismがあったように、Paramorphismの双対としてApomorphismがあります。

apoの場合も同様に可換図式の外側をぐるっと時計回りに辿るように実装します。
apo :: Functor f => (a -> f (Either (Fix f) a)) -> a -> Fix f
apo g = In . fmap (id ||| apo g) . g
ここで|||はControl.Arrowで提供されている
(|||) :: (a -> c) -> (b -> c) -> Either a b -> c
おおよそ上記のような型の演算子です。
Apomorphismの型をよく見るとEitherを使ってこれから組み立てるFix fの型をそのまま返せるような機構が含まれているのが分かります。実はこのショートカットのような仕組みを使うことによってこれから紹介するソートアルゴリズムにおけるナイーブな挿入ソートを通常の挿入ソートの実装にすることが出来るのです。それではいよいよこれまで定義したRecursion Schemesを使って挿入ソートと選択ソートをどのように実装することが出来るのか見ていきたいと思います。
※Recursion Schemesはここで紹介した4つの以外にもまだまだたくさん便利なパターンが存在しており、さらにはモナドやコモナドとの相互作用があったり、全てを統一しようとする大統一理論があったり大変深く面白い世界が広がっている分野です。興味がある人はRecursion Schemesで検索したり、Recursion Schemes - haskell-shoenに俯瞰的にまとめられていたりするので参照してみて下さい。またhaskell-shoenはScrapboxで作られており誰でも編集が出来るので面白い話があればどんどん書き込んでいきましょう ![]()
ソートアルゴリズム再訪
まずソート済みのリストとそうでないリストを区別するためにソート済みのリストを表す型を定義しておきます。
data SListF a r = Nil' | Cons' a r
deriving Functor
-- | ソート済みのリストを表す型
type SList a = Fix (SListF a)
nil' :: SList a
nil' = In Nil'
cons' :: a -> SList a -> SList a
cons' x xs = In (Cons' x xs)
SListFやSListの型を見るとすぐに分かると思いますがListFやListと実質全く同じもので、主にリストがソート済みかどうかを名前で区別出来るように使い分けていきます。
さて準備が整ったのでソートアルゴリズムについて考えていきましょう。一般的なソートアルゴリズムは
sort :: Ord a => List a -> SList a
という型をしています。List aとSList aがFixによって組み立てられていたことを思い出すと、
sort :: Ord a => Fix (ListF a) -> Fix (SListF a)
こうなります。
ところでFix f -> aという型の関数はCatamorphismの結果として作ることが出来たので
sort :: Ord a => Fix (ListF a) -> Fix (SListF a)
sort = cata (? :: Ord a => ListF a (Fix (SListF a)) -> Fix (SListF a))
のようにcataを使って型を分解することが出来ます。この時、cataに適用するために必要な関数?はOrd a => (ListF a (SListF a)) -> Fix (SListF a)という型です。さらにこの?の型はa -> Fix fという型になっており、これはApomorphismの結果として作ることが出来たので3
sort = cata $ apo ??
where ?? :: Ord a => ListF a (Fix (SListF a)) -> SListF a (Either (Fix (SListF a)) (ListF a (Fix (SListF a))))
と分解することが出来ます。最後に型の見え方が対称的になるように??に少し手を加えると、
sort = cata $ apo (??? . fmap (id &&& out))
となり、最終的には
??? :: Ord a
=> ListF a (SList a, SListF a (SList a))
-> SListF a (Either (SList a) (ListF a (SList a)))
という型の関数があればsort関数と同じ型をcataとapoを使って構築できることが分かりました。
(うひゃー見た目が複雑 ![]() ですが心の目を凝らしてみると構造が見えてくるはず…?)
ですが心の目を凝らしてみると構造が見えてくるはず…?)
今度は反対にsortをAnamorphismの結果として出てくる関数だとして見てみましょう。
sort :: Ord a => Fix (ListF a) -> Fix (SListF a)
sort = ana (? :: Ord a => Fix (ListF a) -> SListF a (Fix (ListF a)))
anaに適用するのに必要な関数?はOrd a => Fix (ListF a) -> SListF a (Fix (ListF a))という型になりました。さらにこのFix f -> aという型の関数はParamorphismの結果として作ることが出来たので4
sort = ana $ para ??
where ?? :: Ord a => ListF a (Fix (ListF a), SListF a (Fix (ListF a))) -> SListF a (Fix (ListF a))
と分解することが出来ます。最後に型の見え方が対称的になるように??に少し手を加えると、
sort = ana $ para (fmap (id ||| In) . ???)
となり、最終的には
??? :: Ord a
=> ListF a (List a, SListF a (List a))
-> SListF a (Either (List a) (ListF a (List a)))
という型の関数があればsort関数と同じ型をanaとparaを使って構築できることが分かりました。
2つの分解方法で必要になった結果???の型を目を凝らしてよく見てみると以下のような型を持つ関数が共通して必要になっていることが分かります。
swop :: Ord a => ListF a (x, SListF a x) -> SListF a (Either x (ListF a x))
引数と返り値で、ListF aとSListF aの順番が、そしてタプル(,)とEitherが双対として入れ替わっているのが分かりますね。それではこのswopを実装してみましょう。
swop :: Ord a => ListF a (x, SListF a x) -> SListF a (Either x (ListF a x))
swop Nil = Nil'
swop (Cons a (x, Nil')) = Cons' a (Left x)
swop (Cons a (x, (Cons' b x')))
| a <= b = Cons' a (Left x)
| otherwise = Cons' b (Right $ Cons a x')
このswopが型パズルの最後のピースであり、我々はソートアルゴリズムと同じ型を持つ2つの関数
cata $ apo (swop . fmap (id &&& out))
ana $ para (fmap (id ||| In) . swop)
を手に入れることが出来ました。
しかし本当にこれらはソートアルゴリズムになっているのでしょうか?実際に実行して確かめてみましょう。
> toList' . cata (apo (swop . fmap (id &&& out))) . fromList $ [4, 3, 9, 0]
[0,3,4,9]
> toList' . ana (para (fmap (id ||| In) . swop)) . fromList $ [4, 3, 9, 0]
[0,3,4,9]
見事リストをソートできていますね! ![]()
それではこれら2つのソートアルゴリズムはどういった種類のアルゴリズムになっているのでしょうか?実際の挙動を調べるためにどのようにアルゴリズムが実行されたのかステップ毎にコードを評価して確認していきましょう。
cata - apo - swop
cata (apo (swop . fmap (id &&& out)))
(In (Cons 4 (In (Cons 3 (In (Cons 9 (In (Cons 0 (In Nil)))))))))
cata は第一引数の関数で In を置き換えるような動作をするので、
apo f (Cons 4 (apo f (Cons 3 (apo f (Cons 9 (apo f (Cons 0 (apo f Nil))))))))
のように展開することが出来ます。
まずは内側から、 apo f Nilを評価すると
apo f Nil
== apo (swop . fmap (id &&& out)) Nil
== In . fmap (id ||| apo f) . (swop . fmap (id &&& out)) $ Nil
== In . fmap (id ||| apo f) $ swop Nil
== In $ fmap (id ||| apo f) Nil'
== In Nil'
となり結果の型はソート済みのリストを表すSList aであることが分かります。
次に一つ外側を含めた apo f (Cons 0 (In Nil')) を評価すると、
apo f (Cons 0 (In Nil'))
== In . fmap (id ||| apo f) . (swop . fmap (id &&& out)) $ (Cons 0 (In Nil'))
== In . fmap (id ||| apo f) $ swop (Cons 0 (In Nil', Nil'))
== In $ fmap (id ||| apo f) (Cons' 0 (Left (In Nil')))
== In (Cons' 0 (In Nil'))
となります。
次にさらに一つ外側を含めた apo f (Cons 9 (In (Cons' 0 (In Nil')))) を評価すると、
apo f (Cons 9 (In (Cons' 0 (In Nil'))))
== In . fmap (id ||| apo f) . (swop . fmap (id &&& out)) $ Cons 9 (In (Cons' 0 (In Nil')))
== In . fmap (id ||| apo f) $ swop (Cons 9 (In (Cons' 0 (In Nil')), Cons' 0 (In Nil')))
== In $ fmap (id ||| apo f) (Cons' 0 (Right (Cons 9 (In Nil'))))
== In $ Cons' 0 (apo f (Cons 9 (In Nil')))
== In (Cons' 0 (In (Cons' 9 (In Nil'))))
となりました。swopによって0と9の順番が入れ替えられていますね。
最後にもう一つだけ外側を持ってきて評価してみましょう。
apo f (Cons 3 (In (Cons' 0 (In (Cons' 9 (In Nil'))))))
== In . fmap (id ||| apo f) . (swop . fmap (id &&& out)) $ Cons 3 (In (Cons' 0 (In (Cons' 9 (In Nil')))))
== In . fmap (id ||| apo f) $ swop (Cons 3 (In (Cons' 0 (In (Cons' 9 (In Nil')))), Cons' 0 (In (Cons' 9 (In Nil')))))
== In $ fmap (id ||| apo f) (Cons' 0 (Right (Cons 3 (In (Cons' 9 (In Nil'))))))
== In . Cons' 0 $ apo f (Cons 3 (In (Cons' 9 (In Nil'))))
== In . Cons' 0 $ In . fmap (id ||| apo f) . (swop . fmap (id &&& out)) $ (Cons 3 (In (Cons' 9 (In Nil'))))
== In . Cons' 0 $ In . fmap (id ||| apo f) $ swop (Cons 3 (In (Cons' 9 (In Nil')), Cons' 9 (In Nil')))
== In . Cons' 0 $ In . fmap (id ||| apo f) $ Cons' 3 (Left (In (Cons' 9 (In Nil'))))
== In . Cons' 0 $ In (Cons' 3 (In (Cons' 9 (In Nil'))))
== In (Cons' 0 (In (Cons' 3 (In (Cons' 9 (In Nil'))))))
つまりこのアルゴリズムは内側からソート済みのリストを作り、どんどん一つ外側から要素をとってきて適切な位置まで並べ替えるという処理を繰り返してソートを行っているのです。これはまさに挿入ソートですね!さらにApomorphismのEitherをうまく使うことによって、適切な位置まで要素を挿入したあとの評価は打ち切って無駄な計算をしないような挙動が見て分かるかと思います。
insertSort :: Ord a => List a -> SList a
insertSort = cata $ apo (swop . fmap (id &&& out))
ana - para - swop
ana (para (fmap (id ||| In) . swop))
(In (Cons 4 (In (Cons 3 (In (Cons 9 (In (Cons 0 (In Nil)))))))))
== In . fmap (ana f) . (para (fmap (id ||| In) . swop)) $
(In (Cons 4 (In (Cons 3 (In (Cons 9 (In (Cons 0 (In Nil)))))))))
== In . fmap (ana f) $
(g (Cons 4
( In (Cons 3 (In (Cons 9 (In (Cons 0 (In Nil))))))
, g (Cons 3
( In (Cons 9 (In (Cons 0 (In Nil))))
, g (Cons 9
( In (Cons 0 (In Nil))
, g (Cons 0
( In Nil
, g Nil
)
))
))
))
))
さて大変なことになりましたが怯まずに内側から評価していくことにしましょう。まずは g Nil です。
g Nil
== fmap (id ||| In) . swop $ Nil
== fmap (id ||| In) Nil'
== Nil'
楽勝ですね ![]()
次に外側の g (Cons 0 (In Nil, Nil')) を評価してみましょう。
g (Cons 0 (In Nil, Nil'))
== fmap (id ||| In) . swop $ Cons 0 (In Nil, Nil')
== fmap (id ||| In) $ Cons' 0 (Left (In Nil))
== Cons' 0 (In Nil)
リストのような式が出てきましたがソート済みというわけでもなさそうです。
次にもう一つ外側の g (Cons 9 (In (Cons 0 (In Nil)), Cons' 0 (In Nil)) を評価してみましょう。
g (Cons 9 (In (Cons 0 (In Nil)), Cons' 0 (In Nil))
== fmap (id ||| In) . swop $ (Cons 9 (In (Cons 0 (In Nil)), Cons' 0 (In Nil))
== fmap (id ||| In) $ Cons' 0 (Right $ Cons 9 (In Nil))
== Cons' 0 (In (Cons 9 (In Nil)))
これは面白い挙動をしていますね。つまり返り値を見るとCons'の第一引数にはこれまでの最小値が保持されていて、第二引数の型はList aですが、ここには最小値以外の要素を持つリストがそのまま保持されているという挙動になっていそうです。どこかで見た振る舞いですよね ![]()
念の為、更に外側の g (Cons 3 (In (Cons 9 (In (Cons 0 (In Nil)))), Cons' 0 (In (Cons 9 (In Nil))))) を評価してみましょう。
g (Cons 3 (In (Cons 9 (In (Cons 0 (In Nil)))), Cons' 0 (In (Cons 9 (In Nil)))))
== fmap (id ||| In) . swop $ Cons 3 (In (Cons 9 (In (Cons 0 (In Nil)))), Cons' 0 (In (Cons 9 (In Nil))))
== fmap (id ||| In) $ Cons' 0 (Right $ Cons 3 (In (Cons 9 (In Nil))))
== Cons' 0 (In (Cons 3 (In (Cons 9 (In Nil)))))
予想通り最小値とそれ以外のリストのペアが出来上がっていますね。
この調子で最後まで評価すると全体は、
In . fmap (ana f) . (para (fmap (id ||| In) . swop)) $
(In (Cons 4 (In (Cons 3 (In (Cons 9 (In (Cons 0 (In Nil)))))))))
== In . fmap (ana f) $ Cons' 0 (In (Cons 4 (In (Cons 3 (In (Cons 9 (In Nil)))))))
== In (Cons' 0 (ana f (In (Cons 4 (In (Cons 3 (In (Cons 9 (In Nil)))))))))
となり最小値を一番先頭に持ってきた上でそれ以外のリストに対して再帰的に同様のアルゴリズムを適用しているのが分かるかと思います。これはまさに選択ソートですね!!
selectSort :: Ord a => List a -> SList a
selectSort = ana $ para (fmap (id ||| In) . swop)
ここが山頂です。お疲れさまでした ![]()
我々はsort :: Fix (List a) -> Fix (SList a)関数に対して双対な二つの関数により二通りに分解することにより挿入ソートと選択ソートが得られることを見てきました。つまりこの二つのソートアルゴリズムは双対の関係にあったということなのです!
おまけ: 挿入ソートと選択ソートは本当に双対なのか?
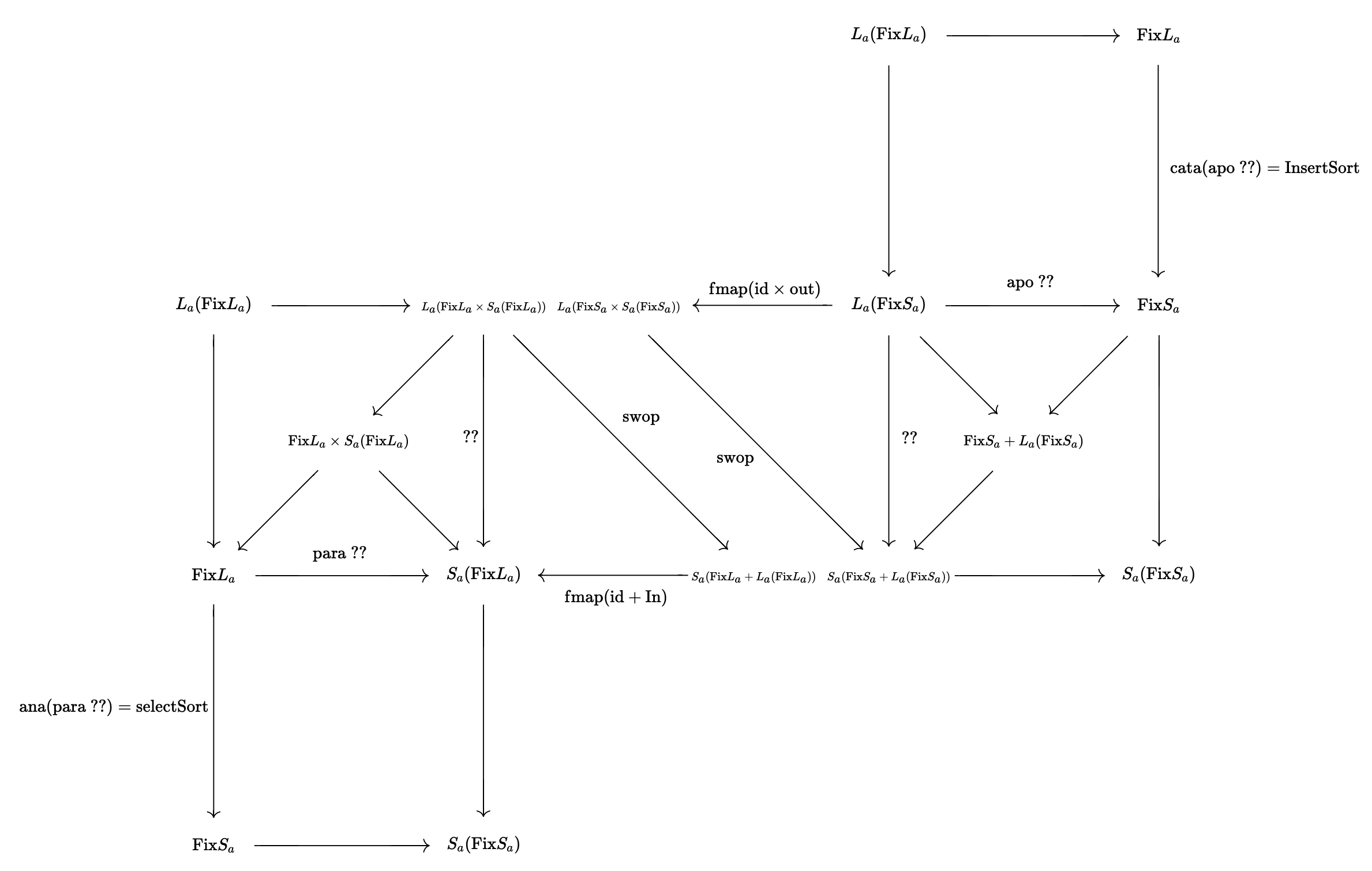
最後に双対の景色を俯瞰して終わりにしましょう。
Catamorphism, Anamorphism, Paramorphism, Apomorphism それぞれの可換図式を組み合わせて、insertSortとselectSortが出来上がる様子を図示しました。図中の$L_a$はListF aであり$S_a$はSListF aを意味しています。二つの図は真ん中のswopのところで別れており、$L_a \cong S_a$であり$+$と$\times$もまた矢印の向きを変えれば入れ替わることに注意すると、片方を180度回転させればちょうど矢印が反対向きになる形でピッタリと重なるのが分かると思います。とても綺麗ですね ![]()
-
実はCatamorphismを使ってParamorphismを実装することも出来るのですがここでは割愛します。可換図式にヒントを入れておくので興味がある人は是非考えてみて下さい。 ↩
-
ここでAnamorphismを選択すると結果はナイーブな挿入ソートになります。 ↩
-
ここでCatamorphismを選択すると結果はバブルソートになります。詳しい解説はRecursion Schemesで考える並べ替えアルゴリズムを参照してみて下さい。 ↩