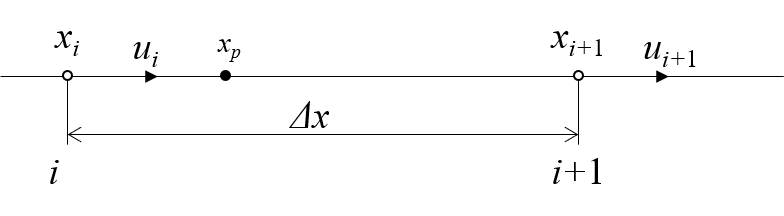Go to Qiita Advent Calendar 2024 Top
LoginSignup
6
6

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

FortranAdvent Calendar 2018

Day 15
@implicit_none

Fortranにおける浮動小数点の丸めと整数化のモード

Last updated at Posted at 2018-12-15

概要

Fortran 2003から浮動小数点の丸めモードを変更できるようになりました．本記事ではそれの簡単な挙動の解説を行います．加えて，浮動小数点の整数化を行うときに似たような話が出てくるので，それについても触れます．最後に，それらを組み合わせることで結果が改善できる問題の例を見ます．
浮動小数点の丸めモードについては他の記事（例えばこちら）も参考にしてください．

使用環境

コンパイラ バージョン
intel Parallel Studio XE Composer Edition for Fortran 17.0.4.210
PGI Visual Fortran for Windows 18.7
gfortran 7.3.0 (for Ubuntu on WSL)

浮動小数点の丸めモード

Fortranでは，実数を取り扱うために，IEEE 754という規格で定められた書式を用いています．浮動小数点は2進数で近似的に表現されているため，厳密な実数値を表すことができません．そのため，実数は規格で定められた書式で表現できる近似値によって代用されます．この近似を丸めとよび，丸めに4通りの方法を指定できます．

丸めモード 丸め方 Fortranでの定数
最近接 丸める実数に最も近い値 ieee_nearest
切り上げ 丸める実数を挟む近傍2点のうち，正の無限大方向の値 ieee_up
切り下げ 丸める実数を挟む近傍2点のうち，負の無限大方向の値 ieee_down
0方向丸め 丸める実数を挟む近傍2点のうち，0方向の値 ieee_to_zero

丸めモードを切り替えるには，サブルーチンieee_set_rounding_mode()を用います．当該サブルーチンとモードを表す定数は，ieee_arithmeticモジュールで定義されています．

program main
    use, intrinsic :: ieee_arithmetic
    implicit none

    call ieee_set_rounding_mode(ieee_nearest) ! 最近接
    call ieee_set_rounding_mode(ieee_up)      ! 切り上げ
    call ieee_set_rounding_mode(ieee_down)    ! 切り下げ
    call ieee_set_rounding_mode(ieee_to_zero) ! 0方向
end program main

基本的に最近接丸めを使っておけば問題ありません．
切り上げと切り下げは，実数の符号によって挙動が変化します．0方向丸めと勘違いしないように注意が必要です．

浮動小数点の足し算を，丸めモードを変えて実行してみます．

program main
    use, intrinsic :: iso_fortran_env
    use, intrinsic :: ieee_arithmetic
    implicit none

    integer :: numItr = 10000
    integer :: i

    real(real64) :: sum

    call ieee_set_rounding_mode(ieee_nearest) ! 最近接
    sum = 0._real64
    do i=1,numItr
        sum = sum + 0.1_real64
    end do
    print '(F25.17)',sum
    
    call ieee_set_rounding_mode(ieee_up) ! 切り上げ
    sum = 0._real64
    do i=1,numItr
        sum = sum + 0.1_real64
    end do
    print '(F25.17)',sum
    
    call ieee_set_rounding_mode(ieee_down) ! 切り下げ
    sum = 0._real64
    do i=1,numItr
        sum = sum + 0.1_real64
    end do
    print '(F25.17)',sum
    
    call ieee_set_rounding_mode(ieee_to_zero) ! ゼロ方向
    sum = 0._real64
    do i=1,numItr
        sum = sum + 0.1_real64
    end do
    print '(F25.17)',sum
    
    call ieee_set_rounding_mode(ieee_nearest) ! 最近接
    sum = 0._real64
    do i=1,numItr
        sum = sum - 0.1_real64
    end do
    print '(F25.17)',sum
    
    call ieee_set_rounding_mode(ieee_up) ! 切り上げ
    sum = 0._real64
    do i=1,numItr
        sum = sum - 0.1_real64
    end do
    print '(F25.17)',sum
    
    call ieee_set_rounding_mode(ieee_down) ! 切り下げ
    sum = 0._real64
    do i=1,numItr
        sum = sum - 0.1_real64
    end do
    print '(F25.17)',sum
    
    call ieee_set_rounding_mode(ieee_to_zero) ! ゼロ方向
    sum = 0._real64
    do i=1,numItr
        sum = sum - 0.1_real64
    end do
    print '(F25.17)',sum
end program main

上のプログラムでは，丸めモードを変えて倍精度実数0.1あるいは-0.1を10000回合計した結果を表示しています．このような複数回の加算を行うと，丸め誤差が混入することが知られています．確かに誤差が混入しており，キリのよい値になっていません．また，丸めモードによって誤差の入り方が変わっていることも確認できます．

   1000.00000000015882051 ! 最近接
   1000.00000000020463631 ! 切り上げ
    999.99999999945578111 ! 切り下げ
    999.99999999945578111 ! 0方向
  -1000.00000000015882051 ! 最近接
   -999.99999999945578111 ! 切り上げ
  -1000.00000000020463631 ! 切り下げ
   -999.99999999945578111 ! 0方向

結果を眺めると，わかることがいくつかあります．

  • 最近接丸めが最も誤差が小さい．
  • 0.1を加算する場合は，切り下げと0方向丸めが同じ結果になる．
  • -0.1を加算する場合は，切り上げと0方向丸めが同じ結果になる．

正確ではありませんが，同一符号の数の加算を行うと，最近接丸めと比較して，切り上げると結果は大きく，切り下げると結果は小さく，0方向に丸めると絶対値が小さくなると判断できます．

浮動小数点の整数化（型変換）

浮動小数点に対して演算を行い，整数を得たいという場面は多くあります．そのような浮動小数点の整数化でも，丸めモードと似た話が出てきます．何が似ているかというと，小数点以下の値を切り上げるか切り捨てるかという丸めの方向です．

Fortran Advent Calendar 1日目の記事で，型変換の関数として，int()とnint()を紹介しました．int()は小数部を切り捨てて，nint()は同符号の最も近い整数へ丸めることで整数化します．実数の丸めモードと比較すると，int()は0方向丸め，nint()は最近接に類似しています．これらの類似性から，丸めモードの切り上げと切り下げに対応する整数化の関数も存在すると予想できます．それらの関数が，ceiling()とfloor()です．ceiling()は小数部を正の無限大方向へ切り上げて，floor()は小数部を負の無限大方向へ切り下げて整数化します．

関数 小数点以下の扱い
int(a=実数[,kind=整数の種別]) 小数点以下を切り捨てる
nint(a=実数[,kind=整数の種別]) 同符号の最も近い整数へ丸める
ceiling(a=実数[,kind=整数の種別]) 正の無限大方向へ丸める
（実数a以上の最小の整数へ丸める）
floor(a=実数[,kind=整数の種別]) 負の無限大方向へ丸める
（実数a以下の最大の整数へ丸める）

いくつかの数を整数に変換して，その挙動を確認してみます．

program main
    use, intrinsic :: iso_fortran_env
    implicit none
    
    real(real64) :: x

    x = -1.5_real64
    print '(F25.17)',x
    print *, int(x),nint(x),floor(x),ceiling(x)

    x = -1._real64 + epsilon(0._real64)
    print '(F25.17)',x
    print *, int(x),nint(x),floor(x),ceiling(x)

    x = -0.5_real64
    print '(F25.17)',x
    print *, int(x),nint(x),floor(x),ceiling(x)

    x = 0.5_real64
    print '(F25.17)',x
    print *, int(x),nint(x),floor(x),ceiling(x)

    x = 1._real64 - epsilon(0._real64)
    print '(F25.17)',x
    print *, int(x),nint(x),floor(x),ceiling(x)
    
    x = 1.5_real64
    print '(F25.17)',x
    print *, int(x),nint(x),floor(x),ceiling(x)
    
end program main

ここで，epsilon(x)（$\varepsilon$）は$1+\varepsilon>1$となる，xと同じ種別の最小の正の数を返します．

出力を表にまとめます．

x int(x) nint(x) floor(x) ceiling(x)
-1.50000000000000000 -1 -2 -2 -1
-0.99999999999999978 0 -1 -1 0
-0.50000000000000000 0 -1 -1 0
0.50000000000000000 0 1 0 1
0.99999999999999978 0 1 0 1
1.50000000000000000 1 2 1 2

int()とnint()は結果が0を中心に反対称的です．floor()とceiling()は，それぞれ負の無限大方向と正の無限大方向の整数へ丸められていることがわかります．

浮動小数点の丸めと整数化が影響する問題

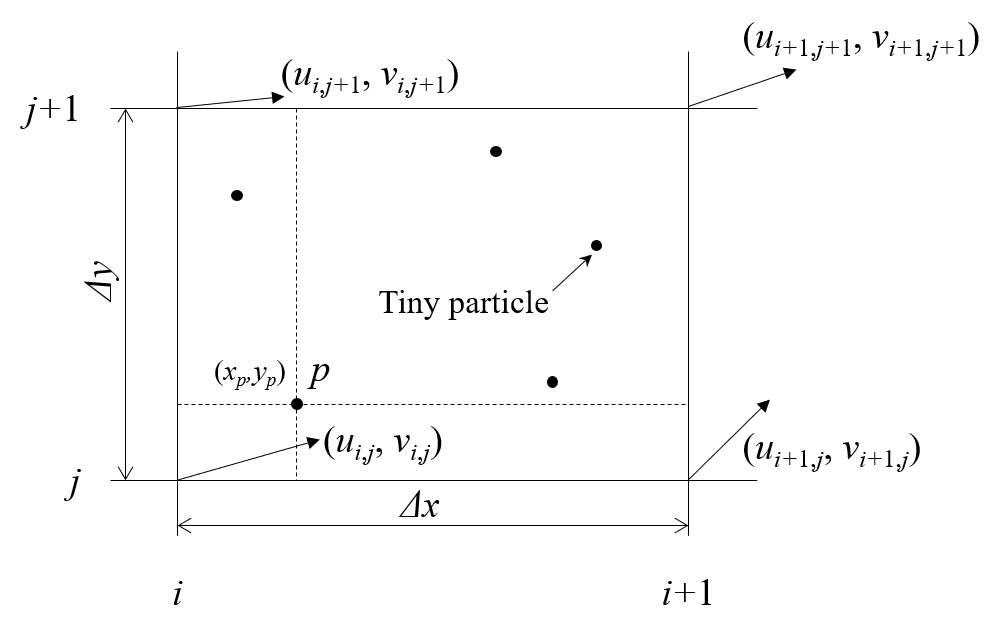
空気中を浮遊する多数の微粒子の挙動を計算によって予測するような問題では，微粒子を質点で近似することがあります．空気の速度は空間を分割する計算格子上で計算し，粒子の速度は近傍格子点の速度を補間することで求めます．粒子の近傍格子点の位置を探す処理が，実数の丸めモードや整数化の関数に影響されます．

簡単のために，格子が矩形で格子点が等間隔とし，さらに$x$軸上の座標のみを考えます．$[0,L_x]$の領域中に粒子$p$が存在しており，その位置は$x_p(>0)$とします．領域中に$N_x$点の格子点を置き，格子点の間隔は$\Delta x$と書くことにします．格子点に$i=1,2,3...$と番号をつけると，格子点の番号$i$と座標値$x_i$との間には，$x_i=(i-1)\Delta x$なる関係が成り立ちます．また，格子点上で速度$u_i$が定義されています．

fig2.png

このような前提で，粒子$p$の速度を計算するために，$x_p$を挟む格子点$ip,ip+1$を探します．最も簡単だと思われるのは，$x_p/\Delta x$を計算して小数点を切り捨てることです．得られた整数に1を足すと，粒子から見て原点に近い格子点が得られます．

    ip   = int(xp/dx) + 1 ! 小数点を切り捨てて粒子の左（原点側）の格子点番号を得る
    xip  = ( ip   -1)*dx  ! 左側の格子点座標
    xip1 = ((ip+1)-1)*dx  ! 右側の格子点座標
    up =   (xip1 - xp )/dx * u(ip)  & ! 距離を重みとした平均で粒子の速度を算出
         + (xp   - xip)/dx * u(ip+1)  !

ほとんどの場合はこれで問題ないのですが，色々と拡張していくと問題が生じます．

  1. 領域が$[-L_x/2, L_x/2]$などになり，負の座標値が現れると，粒子の左側の格子点が求められない．
  2. 粒子座標$x_p$が格子点座標値と重なるか非常に近い場合に，丸めの影響が現れる．

1.は整数化に用いている関数int()が原点方向へ丸めることが原因なので，代わりにfloor()を使えば解決できます．

2.はかなり厄介です．格子点$x_i$上に存在していた粒子が隣の格子点$x_{i+1}$へ移動するような簡単なテストケースを実行してみると，計算過程で誤差が入り，誤った格子点を算出する場合があります．下のプログラムは，11点の格子点で離散化された領域$[0,0.1]$中で，格子点に存在する粒子が一つ隣の格子点に移動する様子を模擬したプログラムです．

program main
    use, intrinsic :: ieee_arithmetic
    implicit none

    real(8),parameter :: Lx = 0.1d0
    integer,parameter :: Nx = 10 + 1
    real(8),parameter :: dx = Lx/dble(Nx-1)
    real(8),parameter :: dt = 0.01d0
    
    real(8) :: u(Nx)
    real(8) :: xp
    integer :: i
    
    u(:) = 1d0 ! 格子点上で定義される空気の速度
    
    do i = 1, Nx
        xp = dble(i-1)*dx ! 格子点iに存在する粒子の座標
        xp = xp + u(i)*dt ! Euler方による時間積分(u(i)*dt=dxなので隣の格子点に移動)

        print '(A,I2,A,F22.18,A,I2)',"particle ",i," at x=",xp,", nearest grid point is",int(xp/dx)+1
    end do
end program main

プログラムを実行してみます．粒子は隣の格子点に移動するので，粒子番号+1の格子点番号が得られていれば正解です．概ね正しく格子点番号を算出できていいますが，粒子7,10は丸め誤算の影響で正しい格子点番号が得られていません．

particle  1 at x=  0.010000000000000000, nearest grid point is 2
particle  2 at x=  0.020000000000000000, nearest grid point is 3
particle  3 at x=  0.029999999999999999, nearest grid point is 4
particle  4 at x=  0.040000000000000001, nearest grid point is 5
particle  5 at x=  0.050000000000000003, nearest grid point is 6
particle  6 at x=  0.060000000000000005, nearest grid point is 7
particle  7 at x=  0.069999999999999993, nearest grid point is 7
particle  8 at x=  0.080000000000000002, nearest grid point is 9
particle  9 at x=  0.089999999999999997, nearest grid point is10
particle 10 at x=  0.099999999999999992, nearest grid point is10
particle 11 at x=  0.110000000000000001, nearest grid point is12

この問題に限れば，int()をnint()に置き換えることで解決します．しかし，速度が場所や時間で変化するような現実の問題では，丸め誤差の影響で値が0.07になっていないのか，あるいは0.06999...が正しいのかを判断できません．ディープラーニングとかいうやつで何とかして

floorで左側に丸めるのか，特別な場合を取りこぼさないようにnint()をうまく使い，負の座標値はifで切り分けるか，格子点番号算出アルゴリズムを変更するか･･･と色々考えた結果，算出アルゴリズは変更せず，粒子が気流速度で移動する計算の丸めモードを変更することにしました．

xp = xp + u(i)*dtの計算の際に丸めモードを切り上げにすることで，最近接丸めより大きめに誤差が入り込むことを期待します．整数化にはfloor()を使います．この方法は，気流速度が正負どちらの場合でも有効に作用すると期待されます．

program main
    use, intrinsic :: ieee_arithmetic
    implicit none

    real(8),parameter :: Lx = 0.1d0
    integer,parameter :: Nx = 10 + 1
    real(8),parameter :: dx = Lx/dble(Nx-1)
    real(8),parameter :: dt = 0.01d0
    
    real(8) :: u(Nx)
    real(8) :: xp
    integer :: i
    
    u(:) = 1d0 ! 格子点上で定義される空気の速度
    
    do i = 1, Nx
        xp = dble(i-1)*dx                         ! 格子点iに存在する粒子の座標
        call ieee_set_rounding_mode(ieee_up)      ! 丸めモードを切り上げに変更
        xp = xp + u(i)*dt                         ! Euler方による時間積分(u(i)*dt=dx)

        print '(A,I2,A,F22.18,A,I2)',"particle ",i," at x=",xp,", nearest grid point is",floor(xp/dx)+1
        
        call ieee_set_rounding_mode(ieee_nearest) ! 丸めモードを最近接丸めに変更
    end do
end program main

実行してみると，粒子7,10の移動先の格子点番号が正しく得られています．

particle  1 at x=  0.010000000000000000, nearest grid point is 2
particle  2 at x=  0.020000000000000000, nearest grid point is 3
particle  3 at x=  0.030000000000000002, nearest grid point is 4
particle  4 at x=  0.040000000000000001, nearest grid point is 5
particle  5 at x=  0.050000000000000003, nearest grid point is 6
particle  6 at x=  0.060000000000000005, nearest grid point is 7
particle  7 at x=  0.070000000000000007, nearest grid point is 8
particle  8 at x=  0.080000000000000016, nearest grid point is 9
particle  9 at x=  0.090000000000000011, nearest grid point is10
particle 10 at x=  0.100000000000000006, nearest grid point is11
particle 11 at x=  0.110000000000000014, nearest grid point is12

速度を1から-1に変更しても結果は同様で，丸めモードと整数化の関数を変更しない場合は何個かの粒子が格子点番号を正しく得られていませんが，丸めモードを変更すると正しく格子点番号を算出できるようになります．

丸めモード未変更
particle  1 at x= -0.010000000000000000, nearest grid point is 0
particle  2 at x=  0.000000000000000000, nearest grid point is 1
particle  3 at x=  0.010000000000000000, nearest grid point is 2
particle  4 at x=  0.019999999999999997, nearest grid point is 2
particle  5 at x=  0.029999999999999999, nearest grid point is 4
particle  6 at x=  0.040000000000000001, nearest grid point is 5
particle  7 at x=  0.049999999999999996, nearest grid point is 5
particle  8 at x=  0.060000000000000005, nearest grid point is 7
particle  9 at x=  0.070000000000000007, nearest grid point is 8
particle 10 at x=  0.080000000000000002, nearest grid point is 9
particle 11 at x=  0.090000000000000011, nearest grid point is10

丸めモード変更後
particle  1 at x= -0.010000000000000000, nearest grid point is 0
particle  2 at x=  0.000000000000000000, nearest grid point is 1
particle  3 at x=  0.010000000000000000, nearest grid point is 2
particle  4 at x=  0.020000000000000000, nearest grid point is 3
particle  5 at x=  0.030000000000000002, nearest grid point is 4
particle  6 at x=  0.040000000000000008, nearest grid point is 5
particle  7 at x=  0.050000000000000003, nearest grid point is 6
particle  8 at x=  0.060000000000000012, nearest grid point is 7
particle  9 at x=  0.070000000000000007, nearest grid point is 8
particle 10 at x=  0.080000000000000002, nearest grid point is 9
particle 11 at x=  0.090000000000000011, nearest grid point is10

残念ながら，これでも万能ではありません．例えば，速度を$1-\varepsilon$（u(:) = 1d0 - epsilon(0d0)）とすると，隣の格子点の若干手前まで移動するので，正しい格子点番号は粒子番号と同じになるはずですが，粒子1以外は正しい粒子座標値を得られていません．

particle  1 at x=  0.009999999999999998, nearest grid point is 1
particle  2 at x=  0.020000000000000000, nearest grid point is 3
particle  3 at x=  0.029999999999999999, nearest grid point is 4
particle  4 at x=  0.040000000000000001, nearest grid point is 5
particle  5 at x=  0.050000000000000003, nearest grid point is 6
particle  6 at x=  0.060000000000000005, nearest grid point is 7
particle  7 at x=  0.070000000000000007, nearest grid point is 8
particle  8 at x=  0.080000000000000016, nearest grid point is 9
particle  9 at x=  0.090000000000000011, nearest grid point is10
particle 10 at x=  0.100000000000000006, nearest grid point is11
particle 11 at x=  0.110000000000000014, nearest grid point is12

ですが，これは非常に厳しい条件です．$10\varepsilon$程度の差があれば，正しく計算できることは確認しています．

まとめ

Fortranにおける浮動小数点の丸めモードを紹介し，それによってどの程度丸め誤差が変わるのかを数値的に確認しました．
また，実数を整数に変換する関数を4種類紹介し，挙動の違いを，浮動小数点の丸めモードと関連付けて確認しました．

最後に，丸めモードが物理シミュレーションの結果に影響する例を紹介しました．この例のような問題は，もっとロバストな方法があるように思うので，もっとよいやり方を知っている方はご教示ください．

雑記

この記事を書くために文献を調べていると，IEEE754-1985において単精度および倍精度実数の名前がsingle precisionおよびdouble precisionであったのが，IEEE754-2008ではbinary32およびbinary64が正式な名前になったということがわかりました．Fortranの型宣言のお作法が定まらないうちに，型名の基準になったであろう規格側が名称を変更しちゃいましたね．

6
6
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
6
6

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?