Fortran IEEE_Arithmetic intrinsic module
Fortran には IEEE754 に関わる制御をするための関数やサブルーチンが用意されています。それらは IEEE_Arithmetic, IEEE_Exceptions, IEEE_features の三つの intrinsic module として提供されています。IEEE754 は近年改定されて、IEEE754-2008 となりましたが、Fortran2003 では基本的に IEEE-1985 に基づいて規格が定められています。
IEEE754 の丸め
Fortran の IEEE754 浮動小数点数の丸めモードとして5つのモードが指定できます。
1.最近接(偶数への丸め)
2.切り上げ
3.切り下げ
4.ゼロ方向への切り下げ
5.これら以外
です。
実数と数直線を同一視するとして、数直線上の不可算無限個の数を、離散有限個の有理数で代表させるわけですが、どのように代表させるかを決めるのが丸めということになります。数直線上に浮動小数点数のメッシュが切られているとして、1.向きによらず最近接の点で代表させるのが最近接、2.+∞側の最近接点で代表させるのが切り上げ、3.-∞側の最近接点で代表させるのが切り下げ、4.原点に向かって最近接の点で代表させるのがゼロ方向への切り下げとなります。
切り上げや、切り下げを多数回繰り返すと、だんだんと丸め誤差が蓄積して、それぞれ正方向と負方向に計算結果がずれてゆくことになりますが、最近接への丸めを取れば誤差が打ち消しあうことが期待されます。
以下で実際に計算して見てみます。
数値計算 Heun法による微分方程式の数値解
ここでは森口繁ー「数値計算工学(1989)」の例題を解いてみます。
解析解が分かっている微分方程式を解いて、数値解との差から誤差の影響を論じます。
微分方程式
${dx\over dt}=-2tx^2,$
の初期値$t=0, x=1$での解析解は、
$x(t)={1\over (1+t^2)}$
となります。
これを Heun(ホイン)法
$s_1 = h\cdot f(t_n,x_n),$
$s_2 = h\cdot f(t_n+h,x_n+s_1),$
$s = (s_1+s_2)/2,$
$x_{n+1}=x_n+s,$
で数値的に解きます。
Heun 法では、誤差が $h^2$ に比例しています。
以下では、積分のステップ $h$ を変えながら、$t=0$ から $t=1$ まで $t$ について積分して $x$ の値を求め、解析解の 0.5 との差を取ってその誤差を求めます。
ソースプログラム
program heun
use, intrinsic :: ieee_arithmetic
implicit none
! integer, parameter :: kd = kind(0.0d0) ! double presicion
integer, parameter :: kd = kind(0.0e0) ! single presicion
real(kd) :: t, x, h, s, s1, s2, xx
integer :: i, k
!
! rounding mode
!
call ieee_set_rounding_mode(ieee_nearest)
! call ieee_set_rounding_mode(ieee_up)
! call ieee_set_rounding_mode(ieee_down)
! call ieee_set_rounding_mode(ieee_to_zero)
!
!
do k = 2, 15
h = 1.0_kd / 2**k
t = 0.0_kd
x = 1.0_kd
do i = 0, 2**k - 1
t = h * i
s1 = h * f(t , x ) ! Heun's method
s2 = h * f(t + h, x + s1) !
s = 0.5_kd * (s1 + s2) !
x = x + s !
end do
write(9, '(i10, es25.15)') k, x - g(t + h) ! t + h = 1.0
end do
stop
contains
pure elemental real(kd) function f(t, x) ! differential equation
real(kd), intent(in) :: t, x
f = -2.0_kd * t * x * x
end function f
pure elemental real(kd) function g(t) ! analytic solution
real(kd), intent(in) :: t
g = 1.0_kd / (1.0_kd + t * t)
end function g
end program heun
最近接への丸め
計算結果をみると分かるように、積分の刻み幅 $h$ が大きいうちは、誤差は $h^2$ に比例して減少してゆきますが、$h=2^{-9}$ から先は、丸め誤差のほうが大きくなってこれ以上改善が見られなくなります。
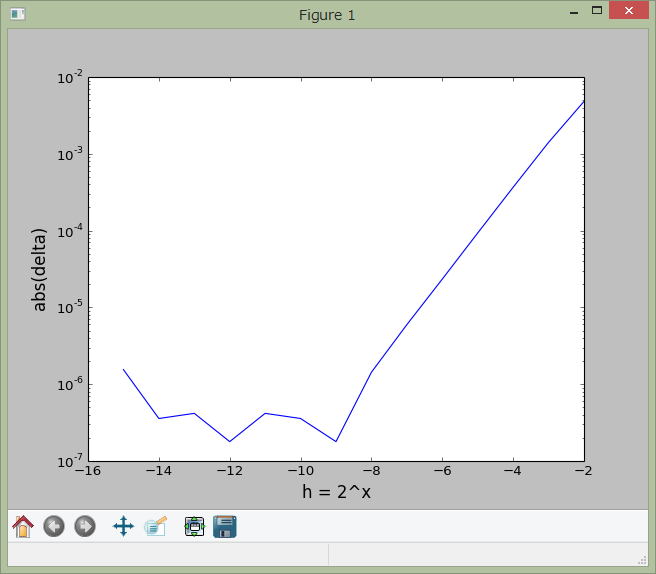
In [23]: plotter('fort.9')
['2', '4.810631275177002E-03']
['3', '1.409411430358887E-03']
['4', '3.668665885925293E-04']
['5', '9.310245513916016E-05']
['6', '2.336502075195312E-05']
['7', '5.960464477539062E-06']
['8', '1.430511474609375E-06']
['9', '1.788139343261719E-07']
['10', '-3.576278686523438E-07']
['11', '-4.172325134277344E-07']
['12', '1.788139343261719E-07']
['13', '-4.172325134277344E-07']
['14', '-3.576278686523438E-07']
['15', '1.549720764160156E-06']
切り上げ
この場合の計算結果をみると、最近接への丸めの場合と違って、丸め誤差が効く領域に入ると誤差が蓄積してゆき、積分の刻み幅 $h$ を減らしてもかえって結果が悪化しています。その傾きは積分のステップの回数 $1/h$ に比例するものと考えられますが、実際計算結果からそのことが確かめられます。
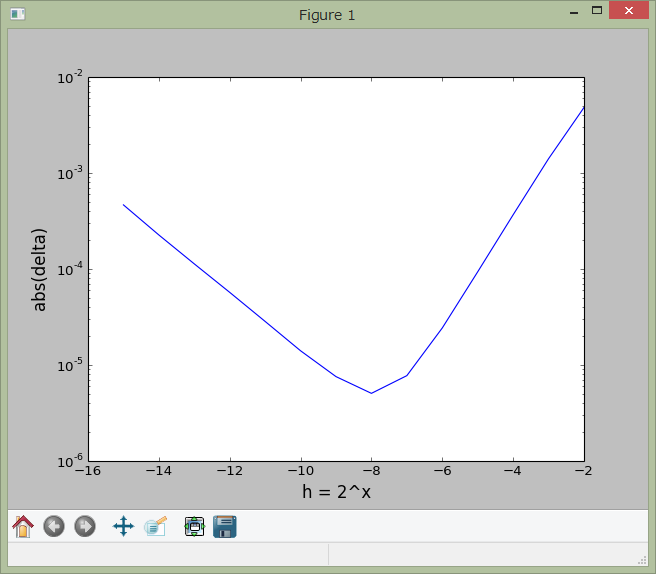
In [24]: plotter('fort.9')
['2', '4.810690879821777E-03']
['3', '1.409471035003662E-03']
['4', '3.671050071716309E-04']
['5', '9.351968765258789E-05']
['6', '2.431869506835938E-05']
['7', '7.748603820800781E-06']
['8', '5.066394805908203E-06']
['9', '7.569789886474609E-06']
['10', '1.406669616699219E-05']
['11', '2.843141555786133E-05']
['12', '5.710124969482422E-05']
['13', '1.130700111389160E-04']
['14', '2.261996269226074E-04']
['15', '4.655718803405762E-04']
切り下げ
切り上げの場合と同様ですが、誤差の蓄積する向きが負の方向になっています。
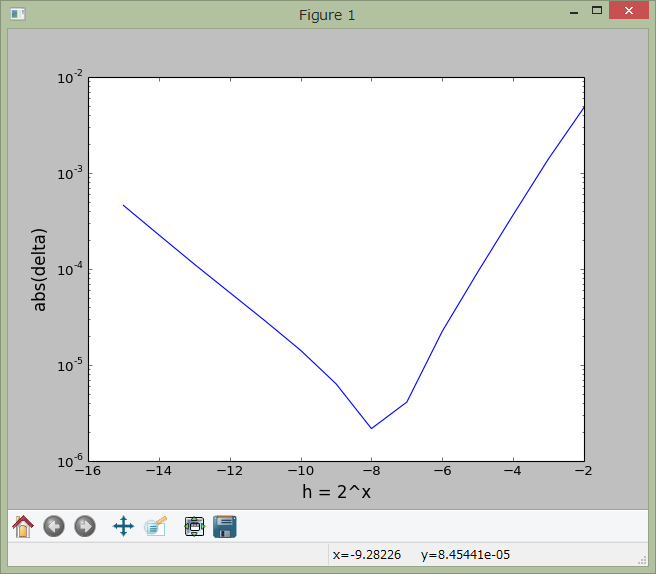
In [25]: plotter('fort.9')
['2', '4.810571670532227E-03']
['3', '1.409351825714111E-03']
['4', '3.666877746582031E-04']
['5', '9.280443191528320E-05']
['6', '2.247095108032227E-05']
['7', '4.112720489501953E-06']
['8', '-2.175569534301758E-06']
['9', '-6.377696990966797E-06']
['10', '-1.424551010131836E-05']
['11', '-2.878904342651367E-05']
['12', '-5.686283111572266E-05']
['13', '-1.123547554016113E-04']
['14', '-2.267360687255859E-04']
['15', '-4.603862762451172E-04']
お絵かきプログラム
(Python よく知らないんで、おかしくても勘弁してね...)
def plotter(fn):
f = open(fn, 'r')
xx = []
yy = []
for line in f.readlines():
line = line.split()
print line
xx.append(-float(line[0]))
yy.append(abs(float(line[1])))
yscale('log')
xlabel('h = 2^x', fontsize = 15)
ylabel('abs(delta)', fontsize = 15)
plot(xx, yy)
f.close()
結論
以上、Fortran での浮動小数点数の丸めモードの制御の実際例と、丸めのモードを変えることで理屈通り計算結果の誤差を制御できることを見ました。
補足
偶数方向への丸め
丸めのモード1.の最近接の場合、丁度二つの浮動小数点数の中間に位置した場合にどうするかという問題が生じます。この場合、偶数方向への丸めを取ることになっています。
偶数方向への丸めに関しては、旧 DEC の Visual Fortran Newsletters の記事「The Perils of Real Numbers (Part 3) by Dave Eklund」を参照してください。
https://software.intel.com/en-us/forums/topic/275071#comment-1548445
偶数への丸めが必要な理由を簡単な例で考えます。いま浮動小数点数の演算を1ビット余分に行い、これを丸める状況を考えます。ここで、単純に0捨1入を行うと、0は元々の数と重なっているので、1を切り上げているのと同じことになります。そこで、偶数方向へ丸めることで、1は正負方向に均等に分配されるようになります。
これは浮動小数点数の離散性から生じる問題で余分なビット数を増やしても、普通の四捨五入的なやり方では確率的に切り上げ方向に向かう結果は変わりません。
森口繁一「数値計算工学(岩波書店1989)」の結果との比較
この本は 1989 年発行で、内容的にはさらに古い時代の結果を用いているものと思われます。1989年の時点では、IEEE754 は大型計算機の分野では全く普及しておらず、この本でも全く触れられていません。
この記事での計算は「数値計算工学」六章を参考にいたしました。ここでの計算と同じ計算をした結果が図6.25に与えられていますが、それはここでの『切り下げ』の場合に酷似した結果になっています。$h$ が大きいところでは $h^2$ に比例して誤差が減少し、$h=2^{-8}$ を境に負の誤差が $1/h$ に比例して増加しています。
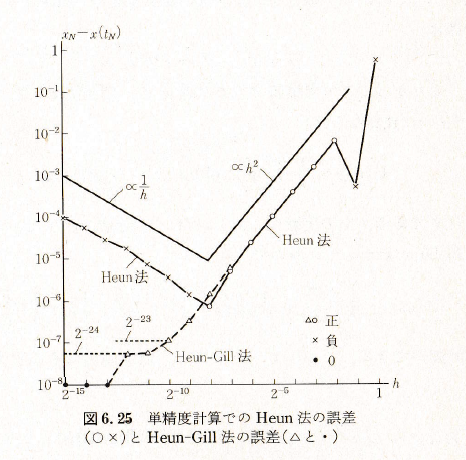
ところが、第六章末の補注 (6.4a)を見ると、この負方向への誤差の蓄積の理由を、丸めの実装が計算機メーカーの誤解による偶数方向への丸めになっているためと結論付けています。著者は0捨1入での丸めを薦めています。(これは切り上げに当たると思われます。)

ここの記述は偶数方向への丸めにからんで気になっていた点でもあり、確認も含めて計算を行ったものですが、私の理解が至らないだけかもしれないので、念のためここに記しておきます。