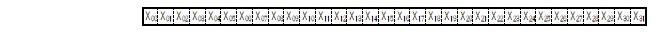CRC 演算を並列処理するための Walma のアルゴリズムの紹介

はじめに

『VHDL で記述する多ビット入力 CRC 生成回路(簡易版)』 では多ビット入力の CRC 生成回路を幾つか紹介しました。上の記事で紹介したいずれの方法でも入力ビット数が大きくなるほど遅延が大きくなり動作周波数が落ちます。しかしながら、CRC を求めるためにはひとつ前の CRC の結果が必要なアルゴリズムのために並列処理やパイプライン処理が出来ず、動作周波数を上げることが出来ません。

そこで登場するのが『"Pipelined Cyclic Redundancy Check (CRC) Calculation", M. Walma, IEEE Computer Communications and Networks, 2007』です。このアルゴリズムを使えば CRC の生成を並列処理またはパイプライン処理することが可能になります。この記事では この Walma のアルゴリズムについて紹介します。

Walma のアルゴリズムの原理

Walma のアルゴリズムの原理を正確に理解するためにはガロア拡大体などの数学の知識が必要です。しかし、筆者の力ではすべてを理解するまでには至りませんでした。そこで、この記事では、原理はわからないけど唱えれば何故か発動する「呪文」として次の３つを紹介します。

• CRC(X xor Y) = CRC(X) xor CRC(Y)
• CRC("0" & X) = CRC(X)
• CRC(X & "0") = H×CRC(X)

呪文その１ CRC(X xor Y) = CRC(X) xor CRC(Y)

最大の難関がこの呪文です。なんでも、「CRC はガロア拡大体 GF(2) のうえで線形性を持つので、入力データを Xと Y、 その CRC を CRC(X) と CRC(Y) とすると、CRC(X + Y) = CRC(X) + CRC(Y) が成り立つ」らしいです。ここで + は GF(2) の上での加算を意味しているため、排他論理和(xor) になります。ここで X と Y は同じサイズのビット配列です。

CRC が CF(2) のうえで線形性を持つためには、CRC の初期値が 0 の場合です。例えば、ZIP などで使われている CRC-32 は初期値が0xFFFFFFFF なのでこれに該当しません。

ホンマかいなと思って次のような Python スクリプトを実行してみると、どうやらホントのようです。

check_crc_xor.py

import numpy
def crc32(data):
  crc = 0x00000000
  for d in data:
    for i in range(8):
      crc_xor_d_bit = (crc & 1) ^ ((d >> i) & 1)
      if (crc_xor_d_bit == 1):
        crc = (crc >> 1) ^ 0xEDB88320
      else:
        crc = (crc >> 1)
  return crc & 0xFFFFFFFF
mismatch_list = []
for i in range(2000):
    size = numpy.random.randint(1,255)
    x    = numpy.random.randint(0,255, (size), numpy.uint8)
    y    = numpy.random.randint(0,255, (size), numpy.uint8)
    if ((crc32(x) ^ crc32(y)) != crc32(x ^ y)):
        mismatch_list.append([x,y])
if len(mismatch_list) == 0:
    print("ok")
else:
    print("mismatch")

shell$ python check_crc_xor.py
ok

呪文その２ CRC("0" & X) = CRC(X)

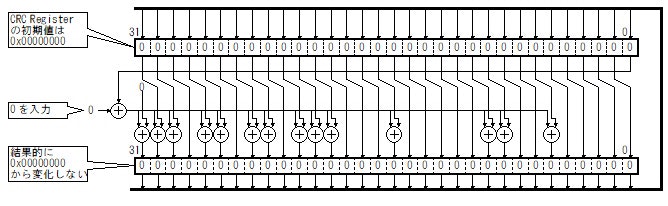
'&' は連接を意味します。つまり "0" & X とは、ビット列 X の前に "0" を追加したビット列になります。ここで登場する CRC() は、初期値が0のものです。そのため、次のように、いくら 0 のデータを入れても CRC の値は0 のままです。

Fig.1 最初に 0 を入力してもCRC は 0x00000000 のまま

したがって、ビット列X の前に "0" をいくつ追加しても CRC の演算結果は変わりません。したがって次の式が成立します。

CRC((0\;to\;N-1\;=>\;'0')\;\&\;X)= CRC(X)

呪文その3 CRC(X & "0") = H×CRC(X)

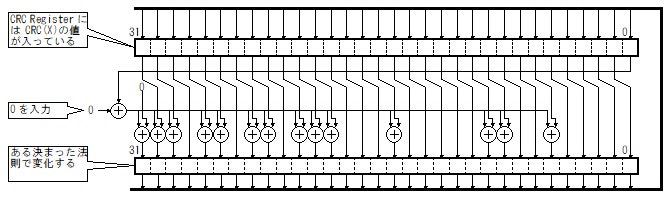
今度はビット列 X の後ろに "0" を追加したビット列の CRC を考えます。次の図のように、CRC Registerにはすでにビット列 X のCRC の値が入っている状態で、さらに "0" を追加すると、何らかの法則で新しい CRC の値が得られます。

Fig.2 X の後ろに 0 を追加した時の CRC

ここで CRC(X) の値を C(0 to 31)の一次元配列、 "0" を追加した時の CRC の値を D(0 to 31) の一次元配列とすると、次の行列式が成立します。

Fig.3 X の後ろに 0 を追加した時の行列式

ここではGF(2) の上での乗算を意味しているため、ビット同士の加算は排他論理和(xor) に、ビット同士の乗算は論理積(and) になります。例えば、D00 = C01、D30 = C00 xor C31、D31 = C31 になります。

この行列式の 32×32 の行列を H、C(0 to 31) を CRC(X)、 D(0 to 31) を CRC(X & '0') とすると、次のように書けます。

CRC(X\;\&\, "0" )= H \times CRC(X)

さらに１個の '0' を後ろに追加すると次のようになります。

\begin{align}
CRC(X\;\&\, "00" ) &= H \times ( H \times CRC(X) ) \\
&= H^2 \times CRC(X)
\end{align}

つまり、ビット列 XにN個の '0' を追加した時の CRC は次のようになります。

CRC(X\;\&\, (0\;to\;N-1\;=>\;'0') ) = H^N \times CRC(X) 

並列化の考え方

1. ビット列 X を用意する

ここでは説明のために32bit 長のビット列 X(0 to 31) の CRC(X(0 to 31)) を計算することを考えます。　

Fig.4 32bit長のビット列 X(0 to 31)

2. ビット列 Xを分割する

次に、この32ビット長のビット列 X(0 to 31) を8ビットずつ４分割することを考えます。

Fig.5 32bit長のビット列 X(0 to 31)を４分割

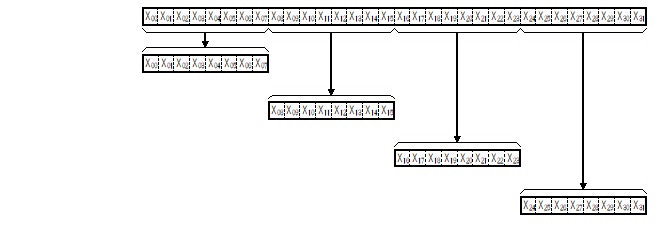
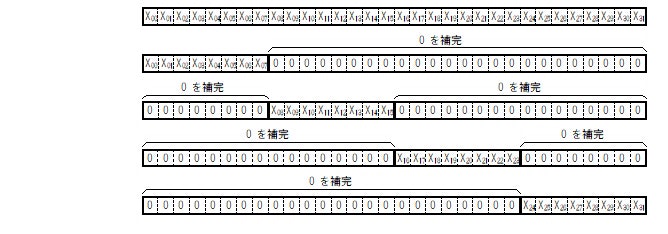
3. 分割したビット列に "0" を補完する

さらに分割した４つの8ビット長のビット列をそれぞれ32ビット長になるように "0" を補完します。

Fig.6 各々 0 を補完

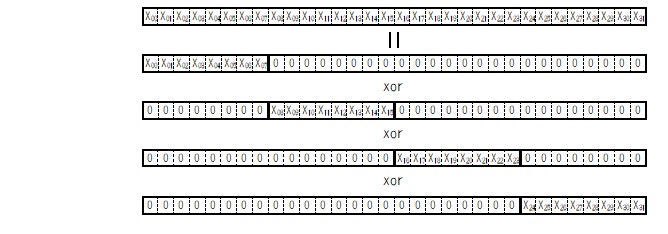
4. 分割して "0" を補完したビット列同士を xor するともとのビット列 X に戻る

ここで A xor 0 = A なので、分割して "0" を補完した4つのビット列を全部 xor すると、もとのビット列 X(0 to 31) に戻ることがわかります。

Fig.7 各々のビット列同士を xor すると X(0 to 31) に戻る

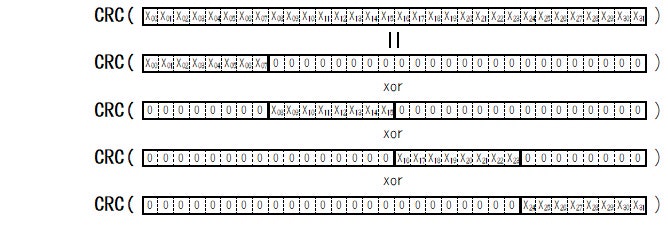
5. ビット列 X の CRC に呪文その１を適用する

ここでビット列 X(0 to 31) の CRC を求めることを考えます。その際、呪文その１、CRC(X xor Y) = CRC(X) xor CRC(Y) を適用することで、次の図のように CRC(X(0 to 31)) は分割して "0" を補完したビット列を各々 CRC 演算した結果を xor した結果になります。

Fig.8 CRC(X) は分割して0を補完したビット列の CRC 同士の xor になる

6. 分割して "0" を補完したビット列の CRC に呪文その２を適用する

さらに分割して "0" を補完したビット列の CRCは、呪文その２ CRC("0" & X) = CRC(X)を適用すると次の図のようになります。

Fig.9 分割して0を補完したビット列の CRC に呪文その２を適用

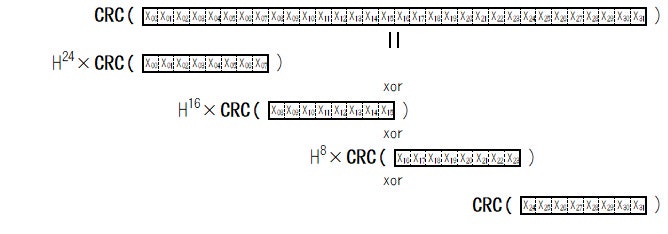
7. 分割して "0" を補完したビット列の CRC に呪文その３を適用する

さらに呪文その３ CRC(X & "0") = H×CRC(X) を適用すると次のようになります。

Fig.10 分割して0を補完したビット列の CRC に呪文その３を適用

8. CRC(X) は並列に処理できるように分割できる

最終的に式で表すと次のようになります。

\begin{align}
CRC(X(0\;to\;31)) =& H^{24} \times CRC(X(0\;to\;7))\;xor\;\\
&H^{16} \times CRC(X(8\;to\;15))\;xor\;\\
&H^{8}\; \times CRC(X(16\;to\;23))\;xor\;\\
&\;\;\;\;\;\;\;\;\;\;CRC(X(24\;to\;31))
\end{align}

この式の素晴らしいところは、各項((H**24)×CRC(X(0 to 7))、(H**16)×CRC(X(8 to 15))、(H**8)×CRC(X(16 to 23))、CRC(X(24 to 31)))が互いに依存せず独立していることです。そのため、各項を並列に演算することができます。

前回の『VHDL で記述する多ビット入力 CRC 生成回路(簡易版)』 で紹介した方法は、CRC を求めるためにはひとつ前の CRC の結果が必要なアルゴリズムのために、並列処理やパイプライン処理が出来ず、動作周波数を上げることが出来ませんでした。

それがこの Walma のアルゴリズムを使えば、並列処理が可能になります。

Walma のアルゴリズムの実装例

ブロック図

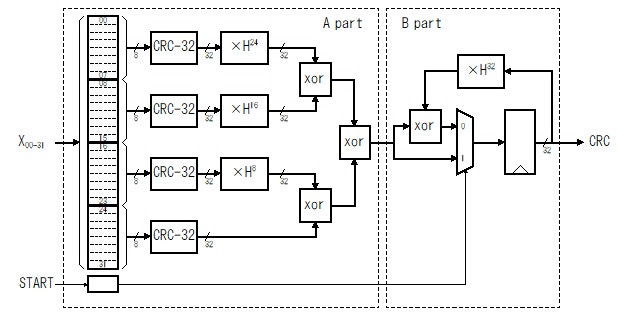
Walma のアルゴリズムを論理回路で実装した例のブロック図を次に示します。この例では1ワード(32ビット)ずつ順次入力されるデータを8ビットずつ４分割して並列に CRC を求めています。最終段のレジスタの出力は H**32 で乗算してフィードバックしています。

Fig.11 Walma のアルゴリズムを論理回路で実装した例のブロック図

このブロック図の A パートは、入力データストリームの１ワード(32ビット)毎のCRCを求めています。１ワード毎のCRC演算であり CRC値を累積しないので、パイプライン処理が可能です。必要に応じてパイプラインレジスタを挿入することで動作周波数を自由に設定することができます。

このブロック図の B パートは、A パートで演算された１ワード毎の CRC 演算結果と、レジスタに保持していた前回までの CRC 演算結果を H**32 で乗算してフィードバックして xor することで CRC の値を入力ストリーム分だけ累積します。

この論理回路での実装例の特徴は、入力データのビット幅を増やしても動作周波数はほとんど変わらない点です。 そのため入力データのビット幅を増やしてスループットをあげることができます。

CRC-32に適用する際の注意点

Walma のアルゴリズムが有効なのは、初期値が0の CRC 演算の場合のみです。しかし、例えば PCI-Express の TLP や zlib で使用されている CRC-32 は初期値が0xFFFFFFFF のものです。そのため、このままでは Walma のアルゴリズムは適用できません。

しかし、入力データストリームの最初の32ビットをビット毎に '0' と '1' を反転することで、初期値が0xFFFFFFFF の CRC 演算を、 初期値が0の CRC 演算に変換することができます。

端数処理について

今回の実装例では、説明を簡単にするために、端数処理を説明しませんでした。端数処理とは、入力データの処理単位が入力データのビット幅よりも小さい時に、最終ワードに無効データを含まれる場合の処理を示します。例えば、ネットワークパケットのデータが8ビット単位であるのに対して、CRC 演算回路の入力ビット幅が32ビット単位だった場合、どうしても最終ワードに無効データ(端数)が含まれる可能性があります。

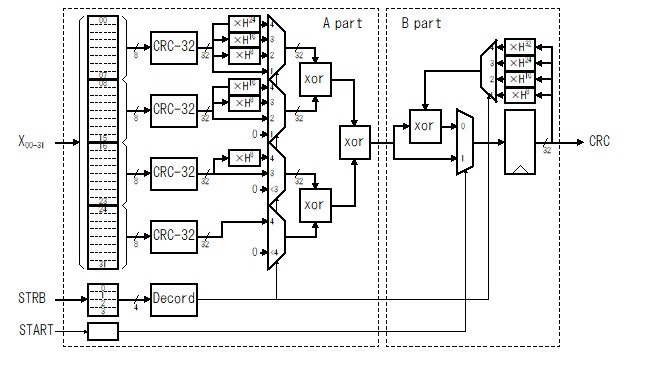
実はこの端数処理がけっこう面倒です。下の図のように H**Nとの乗算を求める回路と、それぞれを選択するためのセレクタが追加されるため、回路が大きく複雑になります。

Fig.12 端数処理を追加した実装例のブロック図

所感

速くなるかどうかはアルゴリズム次第

ちょっと昔話をします。私は仕事で誰かがコンピューターで実装したアルゴリズムを FPGA で実装してみるみたいなことをしていました。で、「スゴいアルゴリズムを考えた。すでにコンピューター上で動いている。けれどちょっと遅い。もっと速くしたいので ASIC で実装したいんだけど検討して欲しい」なんて依頼が来たりします。

言われて見せてもらったソースコード(たいていCで記述されている)が、並列処理なんかまるで考慮されてなかったことがままあります。おそらく最初にアルゴリズムを考えて実装するときは、並列処理のことなんか考えずにとりあえずコンピューターで動作することを第一優先にしてしまっているのでしょう。

しかし、FPGA や ASIC で速く実行するためには、その豊富なリソースを並列に動作させることで達成されます。それなのに並列処理できないようなアルゴリズムを持ってこられても困ります。

それでもなんとか実装してみるのですが、案の定、あんまり性能が出なかったりすると「なんだ、FPGA ってたいしたことないね」なんて言われたりします。「イヤイヤ、なんでも FPGA にすりゃ速くなるもんじゃない。もともとのアルゴリズムがダメだとどうしようもない。コンピューターのプログラムで実装しちゃった時点で手遅れ。」というお話でした。

Walma のアルゴリズムの衝撃

『VHDL で記述する多ビット入力 CRC 生成回路(簡易版)』 で紹介した方法はすべてCRC を求めるためにはひとつ前の CRC の結果が必要なアルゴリズムなので並列処理ができません。つまり「もともとのアルゴリズムがダメだとどうしようもない」典型例でした。

それをひっくり返したのが Walma のアルゴリズムでした。並列化しようとしても出来ないと思われていた CRC 演算が、並列処理可能な演算に変わってしまったのですから。この衝撃が今でも頭に残っていて、今回の記事にしてみようと思った次第です。ま、年寄りの昔話ですが。

しかし、CRC 演算は後に並列化可能なアルゴリズムが見つかったので幸運でした。CRC は 1961年にW. Wesley Peterson が発明したそうです。CRC-32 と一般的に呼ばれている IEEE 802.3 の CRC が定められたのは 1975 年。そのときは並列処理なんて全然考慮されていなかったのでしょう。それに対して Walma のアルゴリズムが発表されたのは 2007 年です。CRC が考案されてから実に40年以上も後のことです。もともとのアルゴリズムがダメだけど、後付けで良いアルゴリズムになった希有な例だと思います。ダメなアルゴリズムのまま消えてしまったり、残ってはいるけど今ではボトルネックになってしまっているアルゴリズムの方が多いのではないでしょうか。

それでも時間が解決することもある

さて、もともと並列処理出来ないと思われていた CRC 演算ですが、Walma のアルゴリズムによって並列演算できるようになりました。では、それまでの並列処理出来ないアルゴリズム(すべてCRC を求めるためにはひとつ前の CRC の結果が必要なアルゴリズム)は意味が無くなったのかといえば、そういうわけではありません。Walma のアルゴリズムは、たしかに高速に演算することが出来るのですが、その分必要なリソースも多くなります。

実はそれまでの並列処理出来ないアルゴリズムでも、今の FPGA では十分な性能を出せたりします。それもこれも FPGA の性能がずいぶん向上したおかげです。用途次第では、結局、単純にループをぶん回したアルゴリズムの方が簡単に書けて良い場合があります。

もともと並列処理できないダメなアルゴリズムだったけど、ハードウェアの性能向上と共に、時を経て再び実用するのに問題なくなってしまった例かもしれません。

お詫び

ホントは、この記事で Walma のアルゴリズムを VHDL で記述した例をあげる予定でしたが、ちょっとアルゴリズムの説明に気合いを入れすぎたせいで、間に合いませんでした。またいつか、別の機会に紹介したいと思います。

参考

• 『VHDL で記述する多ビット入力 CRC 生成回路(簡易版)』 @Qiita
• https://ja.wikipedia.org/wiki/巡回冗長検査
• "Pipelined Cyclic Redundancy Check (CRC) Calculation", M. Walma, IEEE Computer Communications and Networks, 2007