pythonで適当なクラスタを持つサンプルデータを作る

1次元の適当なサンプルを作る

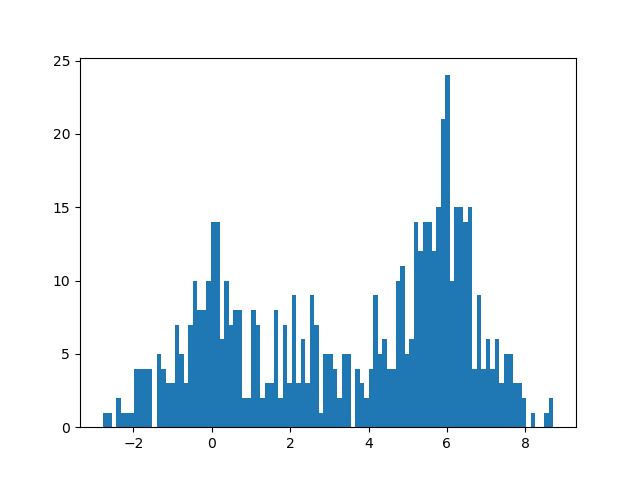
こんな感じの分布のサンプルを作ります

ソースです

import matplotlib.pyplot as plt
import random
import sys

def createDistribution(counter):
    samples = []
    for cnt in counter:
        sample = []
        for i in range(cnt):
            sample.append(random.gauss(0,1))
        samples.append(sample)
    
    y = []
    for i in range(len(counter)):
        for j in range(len(samples[i])):
            y.append(samples[i][j] + i * 3)
    return y

def main():
    # サンプル数を指定、配列数＝クラスタ数と解釈されます
    x = createDistribution([200, 100, 300]);
    plt.hist(x, bins=100)
    plt.savefig("plot1.png");

if __name__ == "__main__":
    main()
# python distribution1.py

y.append(samples[i][j] + i * 3)

i * 3 は３σ分の距離だけクラスタ中心を離しています

２次元の適当なサンプルを作る

こんな感じの分布のサンプルを作ります

ソースです

import matplotlib.pyplot as plt
import random
import sys

def createDistribution(counter):
    xx, yy = [], []
    for cnt in counter:
        ix, iy = [], []
        for i in range(cnt):
            ix.append(random.gauss(0,1))
            iy.append(random.gauss(0,1))
        xx.append(ix)
        yy.append(iy)
    
    x, y = [], []
    for i in range(len(counter)):
        for j in range(len(xx[i])):
            x.append(xx[i][j] + i * 3)
            y.append(yy[i][j] + i * 3)
    return x, y

def main():
    # サンプル数を指定、配列数＝クラスタ数と解釈されます
    x, y = createDistribution([200, 100, 300]);
    plt.scatter(x, y)
    plt.savefig("plot2.png");

if __name__ == "__main__":
    main()
# python distribution2.py

身長体重のサンプルデータを作ってみる

正規分布乱数を利用して身長体重のサンプルデータを作ってみます
こんな感じのデータを作ります

身長	体重
175.481225	68.018599
152.675035	58.921772
174.513797	64.603158
170.562922	76.858922
180.125424	93.762856
177.360964	63.895156
173.432610	52.541947
168.964758	71.661168
175.044804	93.379319

平均身長はこちらを参考にして２０歳の平均身長を使用しました
https://www.e-stat.go.jp/dbview?sid=0003224177

身長別体重の平均と分散はこちらを参考にして適当に決めました
https://www.kumachu.gr.jp/department/other/nutrition/kg.php

ソースです

import io
import numpy as np
import random
import sys

# https://www.e-stat.go.jp/dbview?sid=0003224177
# https://www.kumachu.gr.jp/department/other/nutrition/kg.php
# 身長, 体重, やせ, 肥満
physical_params = [
    [130,37.2,31.3,42.3],
    [131,37.8,31.7,42.9],
    [132,38.3,32.2,43.6],
    [133,38.9,32.7,44.2],
    [134,39.5,33.2,44.9],
    [135,40.1,33.7,45.6],
    [136,40.7,34.2,46.2],
    [137,41.3,34.7,46.9],
    [138,41.9,35.2,47.6],
    [139,42.5,35.7,48.3],
    [140,43.1,36.3,49],
    [141,43.7,36.8,49.7],
    [142,44.4,37.3,50.4],
    [143,45,37.8,51.1],
    [144,45.6,38.4,51.8],
    [145,46.3,38.9,52.6],
    [146,46.9,39.4,53.3],
    [147,47.5,40,54],
    [148,48.2,40.5,54.8],
    [149,48.8,41.1,55.5],
    [150,49.5,41.6,56.3],
    [151,50.2,42.2,57],
    [152,50.8,42.7,57.8],
    [153,51.5,43.3,58.5],
    [154,52.2,43.9,59.3],
    [155,52.9,44.4,60.1],
    [156,53.5,45,60.8],
    [157,54.2,45.6,61.6],
    [158,54.9,46.2,62.4],
    [159,55.6,46.8,63.2],
    [160,56.3,47.4,64],
    [161,57,48,64.8],
    [162,57.7,48.6,65.6],
    [163,58.5,49.2,66.4],
    [164,59.2,49.8,67.2],
    [165,59.9,50.4,68.1],
    [166,60.6,51,68.9],
    [167,61.4,51.6,69.7],
    [168,62.1,52.2,70.6],
    [169,62.8,52.8,71.4],
    [170,63.6,53.5,72.3],
    [171,64.3,54.1,73.1],
    [172,65.1,54.7,74],
    [173,65.8,55.4,74.8],
    [174,66.6,56,75.7],
    [175,67.4,56.7,76.6],
    [176,68.1,57.3,77.4],
    [177,68.9,58,78.3],
    [178,69.7,58.6,79.2],
    [179,70.5,59.3,80.1],
    [180,71.3,59.9,81],
    [181,72.1,60.6,81.9],
    [182,72.9,61.3,82.8],
    [183,73.7,62,83.7],
    [184,74.5,62.6,84.6],
    [185,75.3,63.3,85.6],
    [186,76.1,64,86.5],
    [187,76.9,64.7,87.4],
    [188,77.8,65.4,88.4],
    [189,78.6,66.1,89.3],
]

def near_index(x, n):
    a = (x - n) ** 2
    idx = np.argmin(a)
    return idx

def main():
    params = np.array(physical_params).astype(float)
    params_len = len(params)
    height = params[:,0]
    weight = params[:,1]
    skinny = params[:,2]
    fatness = params[:,3]
    
    # base params # 20歳の身長平均、偏差を使用する
    height_avr = 169.1
    height_var = 6.8
    sample_count = 100
    
    samples = []
    for i in range(sample_count):
        h = random.gauss(height_avr, height_var)
        idx = near_index(height, h)
        weight_avr = weight[idx]
        weight_var = abs(fatness[idx] - skinny[idx]) / 2
        w = random.gauss(weight_avr, weight_var)
        samples.append([h, w])
    s = io.StringIO()
    np.savetxt(s, samples, fmt="%f", delimiter="\t")
    print(s.getvalue())

if __name__ == "__main__":
    main()
# python physical_feature.py

使い道とか

売上とか在庫とかなんでもいいのでダミーデータが件数欲しい時に一応それっぽい分散をしていてほしいとか、そういう時に役に立つかもしれません
後は機械学習系のアルゴリズムの試験やる時にあからさまなクラスターを使用して性能チェックするとかなんとか、そういう時にも役に立つかもしれません

以上です