関連記事
本記事は Geek-Space Advent Calendar 2020 の 7 日目です。（間に合ってない）
- Golang による順列列挙のパフォーマンス研究 1. 再帰を用いたやり方
- Golang による順列列挙のパフォーマンス研究 2. スタックを用いたやり方
- Golang による順列列挙のパフォーマンス研究 3. 繰り上がり法（仮名）
- Golang で順列・組み合わせ・重複順列・重複組み合わせの列挙 （本記事）
はじめに
関連記事にある通り、ここまで順列に関して 3 つのやり方を追求していきました。
今回はこの 3 つのやり方（再帰を用いる、スタックを用いる、繰り上がり法）を、組み合わせ、重複順列、重複組合せにも適用することで、この辺のパターンをひと通り網羅しておこうと思います。
計測は今まで同様、以下のオンボロマシンです：
macOS Big Sur
バージョン 11.0.1
MacBook Air (11-inch, Early 2015)
プロセッサ 1.6 GHz デュアルコアIntel Core i5
メモリ 4 GB 1600 MHz DDR3
go version go1.15.5 darwin/amd64
計測結果は少し編集して、実行時間（ns）、使用メモリ容量（B）、メモリ割り当て数（allocs）を載せます。
コードは全てこちらのリポジトリに上げてあります。（これも今までの記事と同様）
https://github.com/ikngtty/benchmark-go-combinatorics
順列
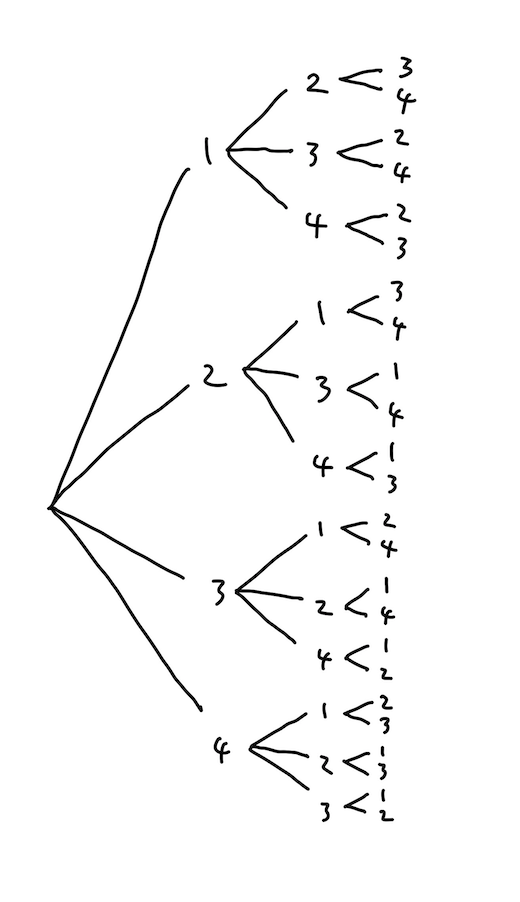
詳しくは関連記事に書いた通りです。ここでは結論をまとめ直していきます。
下準備
以下のコードでパフォーマンスを計測しました：
combinatorics/perm_test.go
func BenchmarkPermutations(b *testing.B) {
const n = 10
const k = 10
doSomethingForPattern := func(pattern []int) {
total := 0
for i := 1; i < len(pattern); i++ {
total += pattern[i] - pattern[i-1]
}
}
targets := []struct {
name string
f func()
}{
{"テスト対象関数の名前",
func() {
// テスト対象関数を用いて、[0, 1, ..., n-1]の数の中からk個選ぶ順列を生成し、
// 各順列に対して`doSomethingForPattern`を行う。
}},
// ...
}
for _, target := range targets {
b.Run(target.name, func(b *testing.B) {
for try := 0; try < b.N; try++ {
target.f()
}
})
}
}
再帰を用いたやり方
最も素直な実装はこんな感じでした。
combinatorics/perm.go
func PermutationsRecursive0(a []int, k int) [][]int {
if k == 0 {
pattern := []int{}
return [][]int{pattern}
}
ans := [][]int{}
for i := range a {
aRest := make([]int, len(a)-1)
for j := 0; j < i; j++ {
aRest[j] = a[j]
}
for j := i + 1; j < len(a); j++ {
aRest[j-1] = a[j]
}
childPatterns := PermutationsRecursive0(aRest, k-1)
for _, childPattern := range childPatterns {
pattern := append([]int{a[i]}, childPattern...)
ans = append(ans, pattern)
}
}
return ans
}
しかし実測結果は以下のようにズタボロ：
PermutationsRecursive0 6338217782 ns 5168828928 B 89707742 allocs
ここから色々改善し、以下のコードにたどり着きました：
combinatorics/perm.go
func PermutationsRecursive6(n, k int, f func([]int)) {
checklist := make([]bool, n)
pattern := make([]int, k)
var body func(pos int)
body = func(pos int) {
if pos == k {
f(pattern)
return
}
for num := range checklist {
if checklist[num] {
continue
}
pattern[pos] = num
checklist[num] = true
body(pos + 1)
checklist[num] = false
}
}
body(0)
}
PermutationsRecursive6 191816791 ns 96 B 2 allocs
スタックを用いたやり方
最終的に、スライスでスタックを実装すると良いことが分かりました。
色々細かくスタックの使い方を変えたりしましたが、スライス版の場合は大してパフォーマンスが変わらないものが多かったです。
なので今回はその中でも一番スタンダードっぽい、「樹形図のノードをスタックに積む」という発想のやつをセレクトします。
combinatorics/perm.go
func PermutationsWithSlice2(n, k int, f func([]int)) {
checklist := make([]bool, n)
patternNodeStack := make([]patternNode2, 1)
pattern := make([]int, k)
patternNodeStack[0] = patternNode2{pos: -1, number: 0}
for len(patternNodeStack) > 0 {
patternNode := patternNodeStack[len(patternNodeStack)-1]
patternNodeStack = patternNodeStack[:len(patternNodeStack)-1]
for i := patternNode.pos; i < k; i++ {
if i > -1 && pattern[i] > -1 {
checklist[pattern[i]] = false
pattern[i] = -1
}
}
if patternNode.pos > -1 {
pattern[patternNode.pos] = patternNode.number
checklist[patternNode.number] = true
}
if patternNode.pos == k-1 {
f(pattern)
continue
}
for num := n - 1; num >= 0; num-- {
if checklist[num] {
continue
}
childNode := patternNode2{
pos: patternNode.pos + 1, number: num,
}
patternNodeStack = append(patternNodeStack, childNode)
}
}
}
PermutationsWithSlice2 186323035 ns 2112 B 8 allocs
繰り上がり法
分かりやすいやつとループをまとめて工夫したやつ、2 つ取り上げます。
combinatorics/perm.go
func PermutationsWithCarrying1(n, k int, f func([]int)) {
checklist := make([]bool, n)
pattern := make([]int, k)
for i := range pattern {
pattern[i] = i
checklist[i] = true
}
for {
f(pattern)
pos := k - 1
for {
if pos == -1 {
return
}
oldNum := pattern[pos]
checklist[oldNum] = false
willBreak := false
for newNum := oldNum + 1; newNum < n; newNum++ {
if checklist[newNum] {
continue
}
pattern[pos] = newNum
checklist[newNum] = true
willBreak = true
break
}
if willBreak {
break
}
pos--
}
for pos++; pos < k; pos++ {
for num := 0; num < k; num++ {
if checklist[num] {
continue
}
pattern[pos] = num
checklist[num] = true
break
}
}
}
}
func PermutationsWithCarrying2(n, k int, f func([]int)) {
checklist := make([]bool, n)
pattern := make([]int, k)
for i := range pattern {
pattern[i] = i
checklist[i] = true
}
pos := k
for pos > -1 {
if pos == k {
f(pattern)
pos--
continue
}
oldNum := pattern[pos]
if oldNum > -1 {
checklist[oldNum] = false
}
willContinue := false
for newNum := oldNum + 1; newNum < n; newNum++ {
if checklist[newNum] {
continue
}
pattern[pos] = newNum
checklist[newNum] = true
pos++
willContinue = true
break
}
if willContinue {
continue
}
pattern[pos] = -1
pos--
}
}
PermutationsWithCarrying1 149944171 ns 96 B 2 allocs
PermutationsWithCarrying2 170103707 ns 96 B 2 allocs
計測結果まとめ
PermutationsRecursive0 6338217782 ns 5168828928 B 89707742 allocs
PermutationsRecursive6 191816791 ns 96 B 2 allocs
PermutationsWithSlice2 186323035 ns 2112 B 8 allocs
PermutationsWithCarrying1 149944171 ns 96 B 2 allocs
PermutationsWithCarrying2 170103707 ns 96 B 2 allocs
組み合わせ
1 桁目の数字 < 2 桁目の数字 < ... < k 桁目の数字 という制約をつければ、あとは順列と同様に列挙することができます。
というか、今までは「x 桁目に使える数字」を考える時に「1 〜 x-1 桁目までに使われた数字を全て把握する」ということが必要でしたが（そのために「使用済み番号チェックリスト」という概念を持ち出したりしました）、今回の場合は「x-1 桁目の数字より上の数字が全部使える」とはっきり分かるので、その辺の処理が一気に楽になります。
ただ、例えば [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] から 6 個選ぶ組み合わせの時に、3 桁目とかに 9 を使ってしまうと、4 桁目以降に使える数字がなくなってしまったりします。一番大きい組み合わせが {4, 5, 6, 7, 8, 9} となるのを考えると、3 桁目の上限は 6 ですね。
この辺を加味すると、[0, 1, ..., n-1] から k 個選ぶ組み合わせにおいて x 桁目に使える数字は、「x-1 桁目の数字より上で、n-1-k+x 以下」となってきます。
ここまで整理できれば実装できたも同然です。
下準備
以下のコードで計測（ほとんど n と k を弄っただけです）：
combinatorics/combi_test.go
func BenchmarkCombinations(b *testing.B) {
const n = 24
const k = 12
doSomethingForPattern := func(pattern []int) {
total := 0
for i := 1; i < len(pattern); i++ {
total += pattern[i] - pattern[i-1]
}
}
targets := []struct {
name string
f func()
}{
{"テスト対象関数の名前",
func() {
// テスト対象関数を用いて、[0, 1, ..., n-1]の数の中からk個選ぶ組み合わせを生成し、
// 各組み合わせに対して`doSomethingForPattern`を行う。
}},
// ...
}
for _, target := range targets {
b.Run(target.name, func(b *testing.B) {
for try := 0; try < b.N; try++ {
target.f()
}
})
}
}
再帰を用いたやり方
素直に書けばこう：
combinatorics/combi.go
// [begin, begin+1, ..., end-1]（半開区間）からk個選ぶ組み合わせ
func CombinationsRecursive0(begin, end, k int) [][]int {
if k == 0 {
pattern := []int{}
return [][]int{pattern}
}
ans := [][]int{}
for num := begin; num < end-k+1; num++ {
childPatterns := CombinationsRecursive0(num+1, end, k-1)
for _, childPattern := range childPatterns {
pattern := append([]int{num}, childPattern...)
ans = append(ans, pattern)
}
}
return ans
}
「x-1 桁目の数字より上の数字が x 桁目に使える数字の範囲」ということで、使える数字を範囲で受け取る形で書いています。
CombinationsRecursive0 5270823668 ns 5060925400 B 70747903 allocs
ここから同様に工夫を凝らすとこうなります：
combinatorics/combi.go
func CombinationsRecursive1(n, k int, f func([]int)) {
pattern := make([]int, k)
var body func(pos, begin int)
body = func(pos, begin int) {
if pos == k {
f(pattern)
return
}
for num := begin; num < n+pos-k+1; num++ {
pattern[pos] = num
body(pos+1, num+1)
}
}
body(0, 0)
}
CombinationsRecursive1 55564969 ns 96 B 1 allocs
処理時間のオーダーが 2 桁違うので笑うしかない。
ちなみに、「x-1 桁目の数字」はわざわざ引数で渡さなくても生成中の組み合わせを見れば分かることなので、これを踏まえれば引数を 1 つ減らすことができます。
combinatorics/combi.go
func CombinationsRecursive2(n, k int, f func([]int)) {
// 0桁目からでも-1桁目の数字を見れるように先頭にダミーを1桁追加している
pattern := make([]int, k+1)
// 生成中の順列には、「まだちゃんと値を入れていない」という情報を
// ちゃんと-1として埋め込む必要が出てきた
pattern[0] = -1
var body func(pos int)
body = func(pos int) {
if pos == k+1 {
f(pattern[1:]) // ダミーを除いて使用
return
}
for num := pattern[pos-1] + 1; num < n+pos-k; num++ {
pattern[pos] = num
body(pos + 1)
}
}
body(1)
}
CombinationsRecursive2 58998589 ns 112 B 1 allocs
なんかむしろ遅くなりました。ボツですね。
スタックを用いたやり方
combinatorics/combi.go
// 順列のコードから流用
type patternNode3 struct {
pos int
number int
}
func CombinationsWithSlice0(n, k int, f func([]int)) {
patternNodeStack := make([]patternNode3, 1)
pattern := make([]int, k)
patternNodeStack[0] = patternNode3{pos: -1, number: -1}
for len(patternNodeStack) > 0 {
patternNode := patternNodeStack[len(patternNodeStack)-1]
patternNodeStack = patternNodeStack[:len(patternNodeStack)-1]
if patternNode.pos > -1 {
pattern[patternNode.pos] = patternNode.number
}
if patternNode.pos == k-1 {
f(pattern)
continue
}
for num := n + patternNode.pos - k + 1; num >= patternNode.number+1; num-- {
childNode := patternNode3{
pos: patternNode.pos + 1, number: num,
}
patternNodeStack = append(patternNodeStack, childNode)
}
}
}
チェックリストが必要なくなったので、ちょっとスッキリしています。
CombinationsWithSlice0 44367916 ns 8256 B 9 allocs
繰り上がり法
こちらも分かりやすいやつとループまとめて工夫したやつの 2 つ用意しました。
combinatorics/combi.go
func CombinationsWithCarrying0(n, k int, f func([]int)) {
pattern := make([]int, k)
for i := range pattern {
pattern[i] = i
}
for {
f(pattern)
pos := k - 1
for {
if pos == -1 {
return
}
oldNum := pattern[pos]
if oldNum == n+pos-k {
pos--
continue
}
pattern[pos]++
break
}
for pos++; pos < k; pos++ {
pattern[pos] = pattern[pos-1] + 1
}
}
}
func CombinationsWithCarrying1(n, k int, f func([]int)) {
pattern := make([]int, k)
for i := range pattern {
pattern[i] = i
}
pos := k
for pos > -1 {
if pos == k {
f(pattern)
pos--
continue
}
oldNum := pattern[pos]
if oldNum == n+pos-k {
pattern[pos] = -1
pos--
continue
}
if oldNum == -1 {
pattern[pos] = pattern[pos-1] + 1
} else {
pattern[pos]++
}
pos++
}
}
順列と比べてだいぶ書きやすくなりましたね。ある桁の値を増やす時、飛び飛びの増え方をすることがなく、必ず 1 増やせばいいだけなのはデカいです。ループで少しずつ増やしながら試すということがなくなっています。
ただし、左向きに繰り上がりしながら値を増やそうとする時と、繰り上げた桁を後から右向きに振り返って埋め直す時の処理が、今回は共通化できず条件分岐しています。まあそれぐらいです。
CombinationsWithCarrying0 36928434 ns 96 B 1 allocs
CombinationsWithCarrying1 49481598 ns 96 B 1 allocs
なんか妙に差が出てる…。
計測結果まとめ
CombinationsRecursive0 5270823668 ns 5060925400 B 70747903 allocs
CombinationsRecursive1 55564969 ns 96 B 1 allocs
CombinationsRecursive2 58998589 ns 112 B 1 allocs
CombinationsWithSlice0 44367916 ns 8256 B 9 allocs
CombinationsWithCarrying0 36928434 ns 96 B 1 allocs
CombinationsWithCarrying1 49481598 ns 96 B 1 allocs
重複組合せ
順番前後して、先に重複組合せを取り上げます。
なぜかというと、重複組合せの列挙は組み合わせの時とほっとんど同じだからです。
組み合わせは 1 桁目の数字 < 2 桁目の数字 < ... < k 桁目の数字 という考え方をしましたが、これを 1 桁目の数字 <= 2 桁目の数字 <= ... <= k 桁目の数字 に変えてしまうだけで重複組合せになります。
なので組み合わせの次に並べたかったというわけです。
[0, 1, ..., n-1] から k 個選ぶ組み合わせにおいて x 桁目に使える数字を考えると、組合わせの時は「x-1 桁目の数字より上で、n-1-k+x 以下」でしたが、今回は「x-1 桁目の数字以上で、n以下」です。もっと簡単ですね。
下準備
また n と k を調整しただけですが、以下のコードで計測：
combinatorics/dup_combi_test.go
func BenchmarkDupCombinations(b *testing.B) {
const n = 18
const k = 9
doSomethingForPattern := func(pattern []int) {
total := 0
for i := 1; i < len(pattern); i++ {
total += pattern[i] - pattern[i-1]
}
}
targets := []struct {
name string
f func()
}{
{"テスト対象関数の名前",
func() {
// テスト対象関数を用いて、[0, 1, ..., n-1]の数の中からk個選ぶ重複組み合わせを生成し、
// 各重複組み合わせに対して`doSomethingForPattern`を行う。
}},
// ...
}
for _, target := range targets {
b.Run(target.name, func(b *testing.B) {
for try := 0; try < b.N; try++ {
target.f()
}
})
}
}
再帰を用いたやり方
素直なやつ：
combinatorics/dup_combi.go
func DupCombinationsRecursive0(begin, end, k int) [][]int {
if k == 0 {
pattern := []int{}
return [][]int{pattern}
}
ans := [][]int{}
for num := begin; num < end; num++ {
childPatterns := DupCombinationsRecursive0(num, end, k-1)
for _, childPattern := range childPatterns {
pattern := append([]int{num}, childPattern...)
ans = append(ans, pattern)
}
}
return ans
}
begin に渡す数字が num+1 ではなく num になり、ループ条件 num < end-k+1 が num < end になっています。そんだけ。
DupCombinationsRecursive0 4282572542 ns 4187600032 B 60615826 allocs
そんで改良：
combinatorics/dup_combi.go
func DupCombinationsRecursive1(n, k int, f func([]int)) {
pattern := make([]int, k)
var body func(pos, begin int)
body = func(pos, begin int) {
if pos == k {
f(pattern)
return
}
for num := begin; num < n; num++ {
pattern[pos] = num
body(pos+1, num)
}
}
body(0, 0)
}
DupCombinationsRecursive1 47771265 ns 80 B 1 allocs
スタックを用いたやり方
combinatorics/dup_combi.go
// 順列のコードから流用
type patternNode3 struct {
pos int
number int
}
func DupCombinationsWithSlice0(n, k int, f func([]int)) {
patternNodeStack := make([]patternNode3, 1)
pattern := make([]int, k)
patternNodeStack[0] = patternNode3{pos: -1, number: 0}
for len(patternNodeStack) > 0 {
patternNode := patternNodeStack[len(patternNodeStack)-1]
patternNodeStack = patternNodeStack[:len(patternNodeStack)-1]
if patternNode.pos > -1 {
pattern[patternNode.pos] = patternNode.number
}
if patternNode.pos == k-1 {
f(pattern)
continue
}
for num := n - 1; num >= patternNode.number; num-- {
childNode := patternNode3{
pos: patternNode.pos + 1, number: num,
}
patternNodeStack = append(patternNodeStack, childNode)
}
}
}
-1 桁目に入れるダミーの数字が -1 から 0 になってたりします。
DupCombinationsWithSlice0 42335223 ns 8240 B 9 allocs
繰り上がり法
combinatorics/dup_combi.go
func DupCombinationsWithCarrying0(n, k int, f func([]int)) {
pattern := make([]int, k)
for {
f(pattern)
pos := k - 1
for {
if pos == -1 {
return
}
oldNum := pattern[pos]
if oldNum == n-1 {
pos--
continue
}
pattern[pos]++
break
}
numToReplace := pattern[pos]
for pos++; pos < k; pos++ {
pattern[pos] = numToReplace
}
}
}
func DupCombinationsWithCarrying1(n, k int, f func([]int)) {
pattern := make([]int, k)
pos := k
for pos > -1 {
if pos == k {
f(pattern)
pos--
continue
}
oldNum := pattern[pos]
if oldNum == n-1 {
pattern[pos] = -1
pos--
continue
}
if oldNum == -1 {
pattern[pos] = pattern[pos-1]
} else {
pattern[pos]++
}
pos++
}
}
pattern には最初の重複組み合わせをセットする必要があるんですが、最初の組み合わせが {0, 1, 2} のような形になるのに対し、最初の重複組合せは {0, 0, 0} のような形になるので、配列を生成した時点でセット完了になっており、そのためセット処理が消えました。
DupCombinationsWithCarrying0 35562403 ns 80 B 1 allocs
DupCombinationsWithCarrying1 48869797 ns 80 B 1 allocs
計測結果まとめ
DupCombinationsRecursive0 4282572542 ns 4187600032 B 60615826 allocs
DupCombinationsRecursive1 47771265 ns 80 B 1 allocs
DupCombinationsWithSlice0 42335223 ns 8240 B 9 allocs
DupCombinationsWithCarrying0 35562403 ns 80 B 1 allocs
DupCombinationsWithCarrying1 48869797 ns 80 B 1 allocs
重複順列
後回しにした重複順列ですが、実は一番簡単です。
なんせ、各桁は他の桁が何を使っているかを全く意識する必要がありません。
全桁独立して考えれば OK です。
もちろんチェックリストも要りません。
下準備
n と k を調整した計測コード：
combinatorics/dup_perm_test.go
func BenchmarkDupPermutations(b *testing.B) {
const n = 8
const k = 7
doSomethingForPattern := func(pattern []int) {
total := 0
for i := 1; i < len(pattern); i++ {
total += pattern[i] - pattern[i-1]
}
}
targets := []struct {
name string
f func()
}{
{"テスト対象関数の名前",
func() {
// テスト対象関数を用いて、[0, 1, ..., n-1]の数の中からk個選ぶ重複順列を生成し、
// 各重複順列に対して`doSomethingForPattern`を行う。
}},
// ...
}
for _, target := range targets {
b.Run(target.name, func(b *testing.B) {
for try := 0; try < b.N; try++ {
target.f()
}
})
}
}
再帰を用いたやり方
素直なやつ：
combinatorics/dup_perm.go
func DupPermutationsRecursive0(n, k int) [][]int {
if k == 0 {
pattern := []int{}
return [][]int{pattern}
}
ans := [][]int{}
for num := 0; num < n; num++ {
childPatterns := DupPermutationsRecursive0(n, k-1)
for _, childPattern := range childPatterns {
pattern := append([]int{num}, childPattern...)
ans = append(ans, pattern)
}
}
return ans
}
DupPermutationsRecursive0 2145949059 ns 2020474264 B 30689223 allocs
改良：
combinatorics/dup_perm.go
func DupPermutationsRecursive1(n, k int, f func([]int)) {
pattern := make([]int, k)
var body func(pos int)
body = func(pos int) {
if pos == k {
f(pattern)
return
}
for num := 0; num < n; num++ {
pattern[pos] = num
body(pos + 1)
}
}
body(0)
}
DupPermutationsRecursive1 23847135 ns 64 B 1 allocs
スタックを用いたやり方
combinatorics/dup_perm.go
// 順列のコードから流用
type patternNode3 struct {
pos int
number int
}
func DupPermutationsWithSlice0(n, k int, f func([]int)) {
patternNodeStack := make([]patternNode3, 1)
pattern := make([]int, k)
patternNodeStack[0] = patternNode3{pos: -1, number: 0}
for len(patternNodeStack) > 0 {
patternNode := patternNodeStack[len(patternNodeStack)-1]
patternNodeStack = patternNodeStack[:len(patternNodeStack)-1]
if patternNode.pos > -1 {
pattern[patternNode.pos] = patternNode.number
}
if patternNode.pos == k-1 {
f(pattern)
continue
}
for num := n - 1; num >= 0; num-- {
childNode := patternNode3{
pos: patternNode.pos + 1, number: num,
}
patternNodeStack = append(patternNodeStack, childNode)
}
}
}
DupPermutationsWithSlice0 23043210 ns 2080 B 7 allocs
繰り上がり法
N 進法そのまんまなので、「繰り上がり」のニュアンスは重複順列が一番よく表れています。
ちなみに「繰り上がった桁を後でなるべく小さい数字で埋め直す」という作業ですが、今回は繰り上がった桁の数字は必ず 0 になるので、繰り上がると分かった時にさっさと 0 を入れてしまえばあとで埋め直す必要すらないです。
combinatorics/dup_perm.go
func DupPermutationsWithCarrying0(n, k int, f func([]int)) {
pattern := make([]int, k)
for {
f(pattern)
pos := k - 1
for {
if pos == -1 {
return
}
oldNum := pattern[pos]
if oldNum == n-1 {
pattern[pos] = 0
pos--
continue
}
pattern[pos]++
break
}
}
}
func DupPermutationsWithCarrying1(n, k int, f func([]int)) {
pattern := make([]int, k)
pos := k
for pos > -1 {
if pos == k {
f(pattern)
pos--
continue
}
oldNum := pattern[pos]
if oldNum == n-1 {
pattern[pos] = 0
pos--
continue
}
pattern[pos]++
pos = k // 右端に一気に飛んで良い
}
}
デッドリー・シンプルですね。
DupPermutationsWithCarrying0 15678811 ns 64 B 1 allocs
DupPermutationsWithCarrying1 22888059 ns 64 B 1 allocs
N 進法表記に変換するやり方
せっかくなのでちょっと特殊解を試します。
[0, 1, ..., n-1] から k 個選ぶ重複順列の列挙は、n 進法表記で k 桁の数字を全て並べる処理と同値です。
なので、10 進法の int をインクリメントしていきながら都度 n 進法に変換することで、重複順列を全て列挙することができます。
順列、組み合わせ、重複組み合わせは全て変則的な n 進法であり、単純な変換は難しい（多分）です。なので、重複順列の場合のみ使えるやり方になってきます。
ちなみに n = 2 として、 2 進法への変換をビット演算で行うと、よくあるビット全探索になります。
combinatorics/dup_perm.go
func DupPermutationsWithBaseConverting0(n, k int, f func([]int)) {
pattern := make([]int, k)
for deciNum := 0; deciNum < Pow(n, k); deciNum++ {
rest := deciNum
for pos := k - 1; pos >= 0; pos-- {
pattern[pos] = rest % n
rest /= n
}
f(pattern)
}
}
combinatorics/util.go
func Pow(base, exponent int) int {
answer := 1
for i := 0; i < exponent; i++ {
answer *= base
}
return answer
}
DupPermutationsWithBaseConverting1 232745482 ns 64 B 1 allocs
残念ながら他より 10 倍ぐらいかかっている模様。
やはり重複順列毎に k 桁全部の値を書き込み直しているのが痛いですね。
計測結果まとめ
DupPermutationsRecursive0 2145949059 ns 2020474264 B 30689223 allocs
DupPermutationsRecursive1 23847135 ns 64 B 1 allocs
DupPermutationsWithSlice0 23043210 ns 2080 B 7 allocs
DupPermutationsWithCarrying0 15678811 ns 64 B 1 allocs
DupPermutationsWithCarrying1 22888059 ns 64 B 1 allocs
DupPermutationsWithBaseConverting1 232745482 ns 64 B 1 allocs
まとめ
実装難易度を振り返ってみると、「重複順列 < 重複組合せ <= 組み合わせ << 順列」と言えそうです。
実はここまで難しい順に進んできたことになります。
今までの順列の実装が難しく感じた人は、一旦こっちの重複順列とかの実装を読んだ方が良いかもしれませんね。
私はこの後、自分用の競プロライブラリとして、再帰を用いたやつをひと通りまとめておく予定です。（再帰のやり方が一番書きやすく、いざという時に弄りやすそうなので。）
色々実装を追求して計測して比較した後なので、「この実装で良いな」とそこそこ自信を持てるようになりました。大満足です。
TODO: 寄せられた情報によると、フィッシャー–イェーツのシャッフルについて調べることで、配列の中身をスワップしながら爆速で順列を列挙する方法が出てくるらしい。そのうち詳しく調べたいところ。
おわり。