関連記事
本記事は Geek-Space Advent Calendar 2020 の 4 日目です。
- Golang による順列列挙のパフォーマンス研究 1. 再帰を用いたやり方 (本記事)
- Golang による順列列挙のパフォーマンス研究 2. スタックを用いたやり方
- Golang による順列列挙のパフォーマンス研究 3. 繰り上がり法(仮名)
- Golang で順列・組み合わせ・重複順列・重複組み合わせの列挙
はじめに
順列や組み合わせといえばこちら:
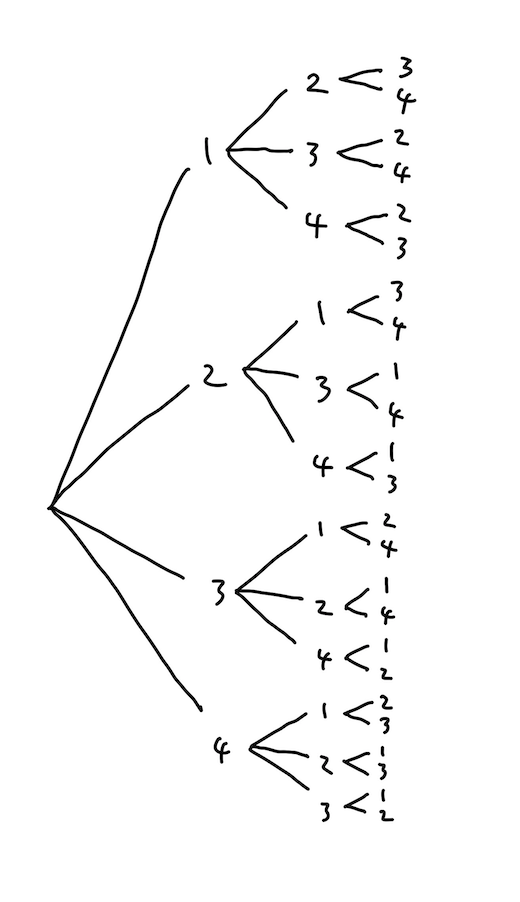
"樹形図"です。
自分は中学受験算数とかで習った覚えがあります。中学受験やってない人はどこで習うんでしょうね。
まあとにかく、人間はこれを描くことで、順列を機械的に列挙していくことができます。
「機械的に列挙できる」ということは、その手順を Golang で書き表せられれば、コンピューターにだって順列が列挙できるはずなわけです。
そこで"樹形図"について考えてみると、これは見ての通り(かつ文字通り)木構造です。
つまり順列の列挙は、「"樹形図"という木構造を生成して探索する作業」と解釈することができます。
木構造の探索には、"深さ優先探索"(Depth-First Search = DFS)と"幅優先探索"(Breadth-First Search = BFS)があります。
順列の列挙に上手く当てはまるのは DFS です。
DFS のやり方には、再帰を用いるやり方と、スタックを用いるやり方とがあります。
この記事では前者について考えていきます。
なお、コードは全てこちらのリポジトリに上げてあります。
https://github.com/ikngtty/benchmark-go-combinatorics
実装
下準備
以下のコードでパフォーマンスを計測していきます:
func BenchmarkPermutations(b *testing.B) {
const n = 10
const k = 10
doSomethingForPattern := func(pattern []int) {
total := 0
for i := 1; i < len(pattern); i++ {
total += pattern[i] - pattern[i-1]
}
}
targets := []struct {
name string
f func()
}{
{"テスト対象関数の名前",
func() {
// テスト対象関数を用いて、[0, 1, ..., n-1]の数の中からk個選ぶ順列を生成し、
// 各順列に対して`doSomethingForPattern`を行う。
}},
// ...
}
for _, target := range targets {
b.Run(target.name, func(b *testing.B) {
for try := 0; try < b.N; try++ {
target.f()
}
})
}
}
計測結果は少し編集して、実行時間(ns)、使用メモリ容量(B)、メモリ割り当て数(allocs)を載せます。
計測は以下のオンボロマシンで行いました:
macOS Big Sur
バージョン 11.0.1
MacBook Air (11-inch, Early 2015)
プロセッサ 1.6 GHz デュアルコアIntel Core i5
メモリ 4 GB 1600 MHz DDR3
go version go1.15.5 darwin/amd64
まずは素直な再帰
// aの中からk個選ぶ順列の列挙
func PermutationsRecursive0(a []int, k int) [][]int {
if k == 0 {
pattern := []int{}
return [][]int{pattern}
}
ans := [][]int{}
for i := range a {
// i番目の項目を抜いた配列を新しく作る
aRest := make([]int, len(a)-1)
for j := 0; j < i; j++ {
aRest[j] = a[j]
}
for j := i + 1; j < len(a); j++ {
aRest[j-1] = a[j]
}
// 再帰
childPatterns := PermutationsRecursive0(aRest, k-1)
for _, childPattern := range childPatterns {
// 各順列の左端にノードをくっつける感じ
pattern := append([]int{a[i]}, childPattern...)
ans = append(ans, pattern)
}
}
return ans
}
- 樹形図の左上のノードを用意する
- そのノードの右に続く樹形図を再帰で作る
- できた樹形図の左端にノードをくっつける
- 1 〜 3 を繰り返して左下のノード分まで縦に並べていく
みたいなイメージです。
木構造の再帰性に沿った、とても素直なコードですね。
測定結果は以下:
PermutationsRecursive0 6376212126 ns 5168828952 B 89707744 allocs
順列の数を先に計算して、配列のメモリ領域をまとめて確保する
上のコードはやりたいことに対してとても素直な実装でした。
パフォーマンスのことはあまり考えていません。
ここから非効率そうなところに目星をつけていき、色々改良を試みていきます。
まず、結果の配列に対して繰り返し append しているのが気になります。
配列の場合、必要な要素数を最初にまとめて確保した方が効率が良いはず。
そのためには、順列についての"場合の数"を計算する必要があります。
数学で言うと nPk って書くやつ。
func PermutationsRecursive1(a []int, k int) [][]int {
if k == 0 {
pattern := []int{}
return [][]int{pattern}
}
// nPk分の空間を確保!
ans := make([][]int, 0, PermutationCount(len(a), k))
for i := range a {
aRest := make([]int, len(a)-1)
for j := 0; j < i; j++ {
aRest[j] = a[j]
}
for j := i + 1; j < len(a); j++ {
aRest[j-1] = a[j]
}
childPatterns := PermutationsRecursive1(aRest, k-1)
for _, childPattern := range childPatterns {
pattern := append([]int{a[i]}, childPattern...)
ans = append(ans, pattern)
}
}
return ans
}
// nPk
func PermutationCount(n, k int) int {
ans := 1
for i := 0; i < k; i++ {
ans *= n - i
}
return ans
}
PermutationsRecursive0 6376212126 ns 5168828952 B 89707744 allocs
PermutationsRecursive1 4109722365 ns 3087847792 B 85046601 allocs
わざわざ nPk を計算している時間を差し引いても、だいぶ速くなりました。
コールバック関数を使って、順列を遅延評価する
「順列をまず全部生成する」というやり方は、全ての順列をメモリに置いておく必要があります。
一方、遅延評価、つまり「順列を 1 つ生成して後続の処理を行わせる。終わったらその順列を破棄し、次の順列を生成する。」というやり方なら、順列 1 個分のメモリしか食わないはずです。
今時の大体の言語には"ジェネレーター関数"という仕組みがあり、これによって要素を遅延評価で少しずつ返してくれるサムシングを作ることができます。
しかし悲しいかな、Golang にそんな仕組みはありません。
代わりに、「1 つの要素に対してやりたいことを記述した関数」を引数として渡してやる方法しかなさそうです。
いわゆる"コールバック関数"というやつ。
func PermutationsRecursive2(a []int, k int, f func([]int)) {
if k == 0 {
pattern := []int{}
// 順列を返すのではなく、コールバック関数に渡す
f(pattern)
return
}
for i := range a {
aRest := make([]int, len(a)-1)
for j := 0; j < i; j++ {
aRest[j] = a[j]
}
for j := i + 1; j < len(a); j++ {
aRest[j-1] = a[j]
}
// 再帰呼び出しの際にもコールバック関数を使うことになる
PermutationsRecursive2(aRest, k-1, func(childPattern []int) {
pattern := append([]int{a[i]}, childPattern...)
f(pattern)
})
}
}
PermutationsRecursive1 4109722365 ns 3087847792 B 85046601 allocs
PermutationsRecursive2 3826715780 ns 2581433088 B 91281951 allocs
(比較したい関数だけ並べています。)
ちょっとメモリ使用量が減り、ちょっと実行時間も減りました。
思ったより「ちょっと」でした。
上では「順列 1 個分のメモリしか食わないはず」と書きましたが、考えてみれば、再帰呼び出しする度に新しい配列を作ったりはしているんですよね。
それと引数 a の配列も再帰呼び出しする度に量産されています。
その辺でのメモリの食い方と比べると、焼け石に水だったのかもしれません。
「使用可能な数字」をチェックリストで管理する
そんなわけで、今度は引数 a (=使用可能な数字群)を量産している点について、なんとかできないか考えてみます。
できれば a をいちいちコピーするのではなく、各再帰呼び出しの間で使い回したいところ。
しかし配列において、「ある項目を除く(そして残りの項目を詰める)」「ある項目を挿入する」という操作は o(N) です。
これでは使い回そうにも効率が悪い。
そこで、使用可能な数字群を []int ではなく「チェックリスト形式」で表現することを考えます。
具体的には
- 使用した数字にチェックを入れる
- まだチェックが入っていない数字を使用可能とする
という感じ。
イメージとしては
before: after:
[0,1,2,3] -> [o,o,o,o]
[0,1,3] -> [o,o,X,o]
[1,3] -> [X,o,X,o]
[1] -> [X,o,X,X]
[] -> [X,X,X,X]
こんな感じです。
チェックリストの型は実際には []bool になります。o と書いた部分が False、X と書いた部分が True です。(普通、逆な気もしますが、「使った数字にチェックマークをつける」というイメージを伝えたかったのでこうなりました。)
この形式だと、値の書き換えだけで「使用可能な数字群」の変化を表現できます。除外や挿入と違い、値の書き換えの操作量は o(1) です。
ただし、編集コストが減った分、参照コストは増えます。
例えば
before: after:
[0,1,2,3,4,5,6,7,8,9] -> [o,o,o,o,o,o,o,o,o,o]
[5] -> [X,X,X,X,X,o,X,X,X,X]
となることを考えると、以前ならたった 1 つの数字 5 を参照するだけだった場面でも、チェックリスト式だと [X,X,X,X,X,o,X,X,X,X] という 10 個の項目を全て調べる羽目になるわけです。
そんなわけで、最終的にどっちの方が速いのか予想がつかないところです。
まあ計算量をしっかり自分で計算すれば分かるのかもしれませんが、なんか難しそうなので、ここはちゃっちゃと実装して測っちゃうことにします。
ここからは表面的な書き方の話。
引数 a の代わりにチェックリストを引数にするのはあまり美しくないです。
チェックリストは実装の都合で生まれたもの。順列を列挙する関数への指示に使うパラメータとしては、あまり自然な形式ではありません。
そこで、引数はただの整数 n (使用可能な数字の個数)あたりにして、チェックリストは関数内部で作ることにします。
ここで問題となるのは、一度作ったチェックリストを再帰呼び出し先にどうやって渡すのか。
チェックリスト作成処理が関数の内部にある以上、普通に再帰呼び出しをすると、呼び出し先でまたチェックリスト作成処理が走るということになります。これではチェックリストを使い回すことができません。
解決策として、再帰呼び出し部分を絞って内部関数として書き、チェックリスト作成処理はその外側に書くことにします。
// [0,1,...,n-1]の中からk個選ぶ順列の列挙
func PermutationsRecursive3(n, k int, f func([]int)) {
checklist := make([]bool, n)
// 再帰用の内部関数
var body func(k int, f func([]int))
body = func(k int, f func([]int)) {
if k == 0 {
f([]int{})
return
}
for num := range checklist {
// チェックの入っている数字はスキップ
if checklist[num] {
continue
}
checklist[num] = true
body(k-1, func(childPattern []int) {
pattern := append([]int{num}, childPattern...)
f(pattern)
})
// きちんと元の状態に戻すのが使い回しのポイント
checklist[num] = false
}
}
body(k, f)
}
こうなりました。
PermutationsRecursive2 3826715780 ns 2581433088 B 91281951 allocs
PermutationsRecursive3 3787541809 ns 2339606912 B 85046640 allocs
結果は僅差でした。
1 つの順列を配列ではなくリストで表す
次は、再帰呼び出しをする度に順列を表現する配列を作り直している点について、改良を試みます。
現状は
[]
-> [2]
-> [1, 2]
-> [0, 1, 2]
という形で配列が作り直されていっています。
要素数 N の配列に対し、左に要素を 1 つ足した新しい配列を作るのに o(N) 分のコストがかかっています。
ここでは、配列ではなくリストを使うことで、左に要素 1 つ足すコストを o(1) にしてみることにします。
Golang はデフォルトではリストが存在しないので、自分で作ってみます。
こんな感じ:
type IntList struct {
first *intListNode
last *intListNode
len int
}
type intListNode struct {
child *intListNode
value int
}
func NewIntList() *IntList {
return &IntList{nil, nil, 0}
}
func (list *IntList) Len() int {
return list.len
}
func (list *IntList) Add(elem int) {
node := intListNode{nil, elem}
if list.first == nil {
list.first = &node
list.last = &node
} else {
list.last.child = &node
list.last = &node
}
list.len++
}
func (list *IntList) Concat(other *IntList) {
if list.first == nil {
*list = *other
} else if other.first == nil {
// Do nothing
} else {
list.last.child = other.first
list.last = other.last
list.len += other.len
}
}
func (list *IntList) Each(f func(elem int)) {
cur := list.first
for cur != nil {
f(cur.value)
cur = cur.child
}
}
func (list *IntList) ToA() []int {
a := make([]int, list.Len())
{
index := 0
list.Each(func(elem int) {
a[index] = elem
index++
})
}
return a
}
この IntList 型を使って順列を表現します。
ただし、最終的には順列は配列である方が使い勝手が良いと思うので、
- 再帰呼び出し中だけリストで順列を表現する
- 左に要素を付け足し続けて完成したリストを、最後に配列に変換してコールバック関数に渡す
という手順で行こうと思います。
func PermutationsRecursive4(n, k int, f func([]int)) {
checklist := make([]bool, n)
var body func(k int, f func(*IntList))
body = func(k int, f func(*IntList)) {
if k == 0 {
f(NewIntList())
return
}
for num := range checklist {
if checklist[num] {
continue
}
checklist[num] = true
body(k-1, func(childPattern *IntList) {
pattern := NewIntList()
pattern.Add(num) // o(1)
pattern.Concat(childPattern) // o(1)
f(pattern)
})
checklist[num] = false
}
}
body(k, func(list *IntList) {
f(list.ToA()) // o(k)
})
}
PermutationsRecursive3 3787541809 ns 2339606912 B 85046640 allocs
PermutationsRecursive4 5024220142 ns 2513788976 B 95933042 allocs
むしろ前よりも遅くなってしまいました。
いちいち変換とかしてるからでしょうか。
1 つの順列を表す配列について、はじめから必要な分のメモリ空間をまとめて確保する
というわけでリストではなく別の策。
最初から配列の要素数を必要な分だけ確保しておくことにより、配列の作り直しを防ぎます。
つまり以下のようなイメージです。
before: after:
[] [ , , ]
-> [2] -> [ , , 2]
-> [1, 2] -> [ , 1, 2]
-> [0, 1, 2] -> [0, 1, 2]
(実際には空白で表した部分にも 0 が入ることになります。int には nil のような値は存在しないので。)
さて、今まで引数 k には「何桁の順列を作りたいか」を渡してきました。
再帰呼び出し先で 1 桁少ない順列を作る際も、この k に 1 減らした数を渡すことで実現しています。
しかし今回、「再帰呼び出し先で何桁の順列を作りたいか」とは別に「最初の呼び出し元は何桁の順列を作りたいのか(=配列の要素数はどれぐらい確保すれば良いのか)」のパラメータも必要になります。
両方を常に引数で渡すという書き方もできますが、実装のためだけに無駄に 2 つのパラメータを指定しなきゃいけないのは、例によって美しくない。
前者は内部関数専用の引数とします。
// 引数`k`が「最初の呼び出し元は何桁の順列を作りたいのか」に相当
func PermutationsRecursive5(n, k int, f func([]int)) {
checklist := make([]bool, n)
// 引数`pos`は「今、順列の何桁目に値を入れようとしているか」。
// 説明文中では「再帰呼び出し先で何桁の順列を作りたいか」が必要と書きましたが、
// 実際にはこちらを引数に取る方が書きやすかったのでこちらにしました。
// 「再帰呼び出し先で何桁の順列を作りたいか」は`k-pos`で計算可能です。
var body func(pos int, f func([]int))
body = func(pos int, f func([]int)) {
if pos == k {
// 要素数を`k`個あらかじめ取りながら配列を生成!
f(make([]int, k))
return
}
for num := range checklist {
if checklist[num] {
continue
}
checklist[num] = true
body(pos+1, func(pattern []int) {
// あらかじめ全桁分の領域が確保されているので、
// 配列へのappendではなく書き込みになりました。
pattern[pos] = num
f(pattern)
})
checklist[num] = false
}
}
body(0, f)
}
PermutationsRecursive3 3787541809 ns 2339606912 B 85046640 allocs
PermutationsRecursive5 1198652505 ns 655839184 B 19728209 allocs
今度こそ改善できました。しかも劇的ですね。速度は 3 倍近いです。
1 つの配列(≒メモリ領域)の使い回しで全部の順列を表現してしまう
ここまで、順列を生成する時のメモリ領域をなるべく使い回すよう考えてきました。
その結果、再帰関数部分の仕事はだんだん「順列用の配列の生成」から「与えられた順列用の配列に値を入れる」という作業に移ってきています。
これを極端に最後まで推し進めてしまいましょう。
つまり、順列用の配列は再帰部分の外側で 1 つ作るのみ。
再帰関数はひたすらこの 1 つの配列相手に値を書き換え続けていきます。
順列用の配列を 1 つしか作らないと、値の書き込み回数も劇的に減ります。
以下の例を見てください。
[0, 1, 2, 3, 4]から3つ選ぶ順列群
before: after:
[ [0, 1, 2], [0, 1, 2]
[0, 1, 3], -> [_, _, 3]
[0, 1, 4], -> [_, _, 4]
[0, 2, 1], -> [_, 2, 1]
[0, 2, 3], -> [_, _, 3]
[0, 2, 4], -> [_, _, 4]
[0, 3, 1], -> [_, 3, 1]
[0, 3, 2], -> [_, _, 2]
[0, 3, 4], -> [_, _, 4]
[0, 4, 1], -> [_, 4, 1]
[0, 4, 2], -> [_, _, 2]
[0, 4, 3], -> [_, _, 3]
[1, 0, 2], -> [1, 0, 2]
[1, 0, 3], -> [_, _, 3]
[1, 0, 4], -> [_, _, 4]
... ...
[4, 3, 0], -> [_, 3, 0]
[4, 3, 1], -> [_, _, 1]
[4, 3, 2] ] -> [_, _, 2]
左は [ [順列], [順列], ..., [順列] ] という形で、配列を順列の数だけ作っていることを示しており、右は [順列] -> [順列] -> ... -> [順列] という形で、1 つの配列を徐々に書き換えていっていることを示しています。
そしてここがポイントなのですが、右で _ と示している部分は、書き換え前の値と同じなので特に書き換える必要がない箇所です。
ご覧の通り、半分以上(多分)の値を書き込まずに済ませることができています。
func PermutationsRecursive6(n, k int, f func([]int)) {
checklist := make([]bool, n)
pattern := make([]int, k)
var body func(pos int)
body = func(pos int) {
if pos == k {
f(pattern)
return
}
for num := range checklist {
if checklist[num] {
continue
}
// 以前は再帰呼び出しで生成された順列群の1つ1つに対して、
// 「左端にノードを加える」という作業が必要でした。
// 今回は「左端の値を書き換える」という作業を事前に1回行って、
// あとは再帰呼び出しに全部任せるだけでOKです。
// そのためコールバック関数を再帰部分に渡したりする手間がなくなりました。
pattern[pos] = num
checklist[num] = true
body(pos + 1)
checklist[num] = false
}
}
body(0)
}
PermutationsRecursive5 1198652505 ns 655839184 B 19728209 allocs
PermutationsRecursive6 191816791 ns 96 B 2 allocs
そんなわけで 6 倍近く速くなりました。メモリの改善に関しては比べ物にならないですね。
コードもなんか紆余曲折あった末、割とすっきりしたところに落ち着いた感じがします。
さて、1 つの配列(≒メモリ領域)を使い回しているこの実装は、使い方に注意する必要があります。
以下のようにコールバック関数の中で受け取った順列を即時使い捨てるのであれば問題はないんですが:
PermutationsRecursive6(3, 2, func(pattern []int) {
fmt.Println(pattern)
})
// Output:
// [0 1]
// [0 2]
// [1 0]
// [1 2]
// [2 0]
// [2 1]
以下のように順列のスライスを溜めておいて後で使おうとすると大変なことになります:
perms := make([][]int, 0, 6)
PermutationsRecursive6(3, 2, func(pattern []int) {
perms = append(perms, pattern)
})
fmt.Println(perms)
// Output:
// [[2 1] [2 1] [2 1] [2 1] [2 1] [2 1]]
こうなってしまうのは、スライスが配列に対する参照でしかないからですね。
上記コードは同じ配列への参照を延々溜めているだけです。
その配列は繰り返し値を書き換えられた結果、最後の順列 [2 1] の形に終着しています。
なので、出力結果は [2 1] が延々と並ぶ形になるわけです。
順列を全部溜めておきたかったら、コールバック関数に渡された時点での配列の値を都度新しい配列にコピーして保存しておく必要があります:
perms := make([][]int, 0, 6)
combinatorics.PermutationsRecursive6(3, 2, func(pattern []int) {
// 新しい配列を用意
patternClone := make([]int, len(pattern))
// 現時点の順列の値を新しい配列に避難させる
copy(patternClone, pattern)
// 新しい配列への参照を溜めておく
perms = append(perms, patternClone)
})
fmt.Println(perms)
// Output:
// [[0 1] [0 2] [1 0] [1 2] [2 0] [2 1]]
チェックリストを捨て、生成途中の順列配列から次に使用可能な数字を判断する
上の改良によって、樹形図を作る順番がしれっと変わりました。
以前は右のノードから順番に埋めていくイメージだったのが、左のノードから埋めるようになっています。
ということは、生成途中の順列配列を見れば、より左側のノードにはどの数字を使っていて、残りの使用可能な数字はどれなのか判断できることになります。
もう checklist は要らないのでは?
ということで実装してみました:
func PermutationsRecursive7(n, k int, f func([]int)) {
pattern := make([]int, k)
var body func(pos int)
body = func(pos int) {
if pos == k {
f(pattern)
return
}
for num := 0; num < n; num++ {
// 数字が使われていたらスキップ
willContinue := false // 大域脱出用
for i := 0; i < pos; i++ {
if pattern[i] == num {
// 大域脱出
willContinue = true
break
}
}
// 大域脱出
if willContinue {
continue
}
// 数字が未使用だと分かり、安心してノードを埋める
pattern[pos] = num
body(pos + 1)
}
}
body(0)
}
PermutationsRecursive6 191816791 ns 96 B 2 allocs
PermutationsRecursive7 741371156 ns 80 B 1 allocs
使用メモリのわずかな改善と引き換えに、めちゃくちゃ遅くなってしまいました。
チェックリストはやはり必要なようです。
まとめ
結論実装は以下:
func PermutationsRecursive6(n, k int, f func([]int)) {
checklist := make([]bool, n)
pattern := make([]int, k)
var body func(pos int)
body = func(pos int) {
if pos == k {
f(pattern)
return
}
for num := range checklist {
if checklist[num] {
continue
}
pattern[pos] = num
checklist[num] = true
body(pos + 1)
checklist[num] = false
}
}
body(0)
}
計測結果を全て並べておきます:
PermutationsRecursive0 6338217782 ns 5168828928 B 89707742 allocs
PermutationsRecursive1 4109722365 ns 3087847792 B 85046601 allocs
PermutationsRecursive2 3807560486 ns 2581434768 B 91281958 allocs
PermutationsRecursive3 3787541809 ns 2339606912 B 85046640 allocs
PermutationsRecursive4 5024220142 ns 2513788976 B 95933042 allocs
PermutationsRecursive5 1198652505 ns 655839184 B 19728209 allocs
PermutationsRecursive6 191816791 ns 96 B 2 allocs
PermutationsRecursive7 741371156 ns 80 B 1 allocs