1. はじめに
これまで、ビジネスにおいて何らかの施策を実施したときの効果検証の手法として、差分の差分法や、傾向スコアを用いた分析法を紹介してきました。今回の記事では、施策の効果の時間的な変化を検証したい場合に有用な、CausalImpactという手法を紹介します。
ここでは、ウェブマーケティングを例にとり、ネット通販会社が売上アップを目指してウェブ広告を配信する状況を考えます。このとき、ウェブ広告配信施策の効果を適切に検証するにはどうすればよいでしょうか。一つの方法として、以前の記事でご紹介した、差分の差分法を利用することが考えられます。この手法は、ウェブ広告の配信対象者と非対象者の、施策実施前後の売上データを使って、施策によってどれだけ売上が増えたかを検証する手法です（詳細はこちらの記事をご覧ください）。もっともシンプルな差分の差分法は、施策実施前後の2時点の売上に着目し、施策実施前の一定期間の売上データと、施策実施後の一定期間の売上データを集約して利用します。売上データを集約する際の期間（施策実施前とはいつからの期間か、また、施策実施後とはいつまでの期間か）は、決算のタイミングなど、ビジネス上意味のある時点などをもとに適切に決定すべきですが、一方で、日次や週次など、より短い時間粒度で施策の効果をモニタリングしたいというニーズもあるでしょう。たとえば、広告配信から数日間は売上がアップするが、その後は売上の増加は見込めないといったことがわかれば、広告の配信期間を工夫することで、無駄なコストを削減することができます。日次の売上データのように、連続的・継続的に取得できるデータ（時系列データと呼びます）をもとに、施策の効果の時間的な変化を捉えるための手法の一つがCausalImpactです。
2. CausalImpactとは
CausalImpactは、日次の売上データなどの時系列データに対し、ウェブ広告配信などの施策（介入と呼びます）の効果がどの程度あるかを推定するための手法の一つです。
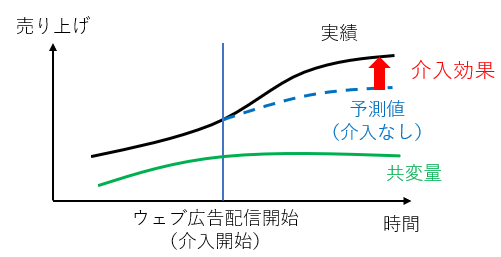
効果検証において興味がある売上などの指標（結果変数と呼びます）が、仮に介入がなかったとしたらどう推移していたかを予測し、結果変数の実績とその予測値の差分を介入の効果と見做します（図１）。仮に介入がなかった場合の結果変数の予測値は、実際には起こらなかったことを仮想的に考えることから反実仮想（counterfactual）と呼ばれます。反実仮想を考える必要がある理由は、介入があった場合は介入があった場合の結果変数の実績（例：ウェブ広告を見た顧客がウェブ広告を見た場合の購買データ）しか得られず、介入がなかった場合の結果変数の実績（例：ウェブ広告を見た顧客がウェブ広告を見なかった場合の購買データ）は得られないためです。後者のデータが得られないのであれば、介入対象でなかった顧客のデータを使えばよいのではと思われるかもしれませんが、特にターゲットを絞って広告配信をしている場合など、介入対象者と非対象者でそもそも購買行動が異なると想定される場合は、「介入対象者に介入しなかった場合の購買データ」と「非対象者の購買データ」を同一視することは適切ではないでしょう。
CausalImpactは反実仮想を予測するために、ベイズ構造時系列モデルと呼ばれる、時系列データを扱うことができるモデルを構築します。モデルの構築には、介入前後の結果変数の時系列データ、および反実仮想の予測に役立ちそうなデータ（共変量と呼びます）を利用します。モデルの詳細は割愛しますが、結果変数の時間変化を表現する状態空間モデルや、時系列データ分析でよく利用されるローカル線形トレンド、さらに共変量を使った回帰モデルを組み合わせています。共変量は、介入の影響を受けず、介入前後で結果変数との関係が変わらないものを選ぶ必要があります。ウェブ広告の効果検証の例では、顧客の年齢や性別など、検証対象の期間中に変化しないような顧客属性などは共変量として採用できる場合が多いでしょう。
図１：CausalImpactで推定される介入効果
3. 実装例
CausalImpactを使った効果検証のイメージをつかんでいただくため、簡単な実装例を示します。CausalImpactは、RやPythonのパッケージで利用することができますが、ここではRでの実装例を示します。以下、
- R 4.2.0
- CausalImpact 1.2.7
を使用しています。
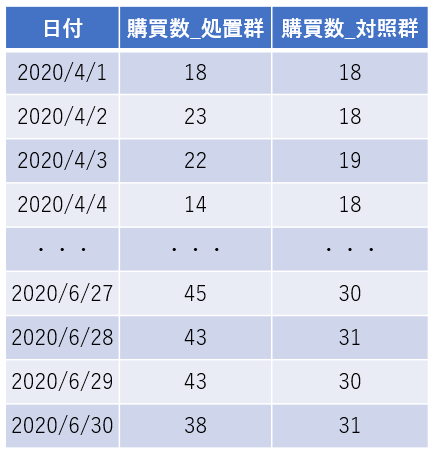
例として、ある商品の日次購買数のサンプルデータを作成し利用します。ここでは、2020年4月～6月の日次購買数が得られており、2020年6月1日から施策を開始し、それによって1日当たり10個購買数が増加した状況を想定したサンプルデータを作成します。また、共変量として、施策の非対象者集団の購買数を用います（図２）。ここで、施策対象の顧客集団を処置群、施策の対象でない顧客集団を対照群と呼んでいます。
図２：商品購買数のサンプルデータ
以下のコードのように、Rで時系列データを扱うためのzoo型のデータとして、上記のデータをdataに読み込みます。施策開始前の期間pre.periodとして2020年4月～2020年5月、施策開始後の期間post.periodとして2020年6月を指定します。これを使って、モデルimpactを構築できます。
data <- read.csv.zoo("sample.csv", read = read.csv)
pre.period <- as.Date(c("2020-04-01", "2020-05-31"))
post.period <- as.Date(c("2020-06-01", "2020-06-30"))
impact <- CausalImpact(data, pre.period, post.period)
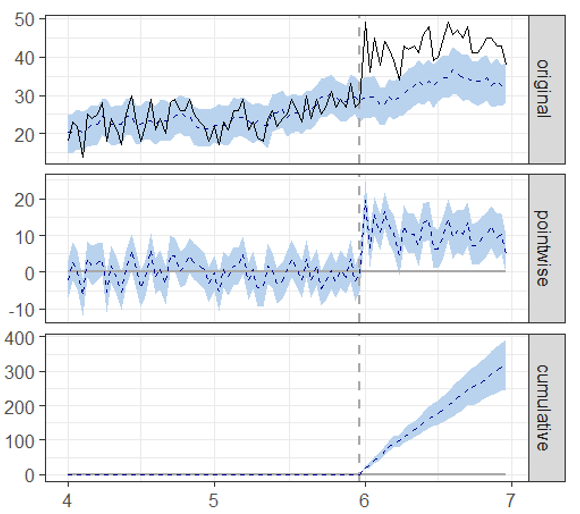
plot()関数を使うことで、CausalImpactによる効果検証結果を可視化することができます（図３）。図３の上図は、処置群の購買数の推移（黒色の実線）と、仮に施策が行われなかった場合の予測値の推移（青色の点線）を示しています。水色の帯は、予測値の信頼区間を示しています。図３の中図は、介入効果、すなわち処置群の購買数と予測値の差分を示しています。2020年6月1日以降に着目すると、介入効果は10付近で推移しており、介入効果が正しく推定できていることがわかります。図３の下図は、介入効果の累積を示しています。累積介入効果の信頼区間（水色の帯）がゼロ（灰色の横線）を含む時点がある場合、その時点では有意な介入効果がないと見做すことができます。
plot(impact)
図３：CausalImpactによる効果検証結果の可視化
さらに、summary()関数を使うことで、効果検証結果の数表を得ることができます（図４）。Averageという列は、施策開始後の平均値、Cumulativeという列は累積値であることを示しています。また、Actualという行は施策開始後の処置群の結果変数を示しており、Prediction, Absolute effect, Relative effect は、それぞれ施策を行わなかった場合の予測値、介入効果、相対的な介入効果を、標準偏差と95%信頼区間とともに示しています。Absolute effect行のAverage列に着目すると、値は11となっており、介入効果が平均11と推定されたことが見て取れます。
summary(impact)
図４：CausalImpactによる効果検証結果
ここまでの実装例では、CausalImpactパッケージのデフォルト設定でモデルを構築しましたが、パラメータを調整することで、分析対象のデータの傾向を加味したより高度なモデルを構築することもできます。パラメータの一例を以下に示します。
- standardize.data：データを標準化させて使用するか否か（デフォルトはTRUE）。
- prior.level.sd：ローカル線形トレンドの標準偏差（デフォルトは0.01）。
- nseasons：季節性の周期（デフォルトは1（季節性なし））。複数の季節性を同時に導入できない点に注意が必要。
- season.duration: 季節性を導入した場合の、1シーズン中のデータ数（デフォルトは1）。
- dynamic.regression：時変回帰係数を含める（共変量に対する回帰係数を時間変化させる）か否か（デフォルトはFALSE）。
4. CausalImpactの特徴と注意点
4.1. 差分の差分法との比較
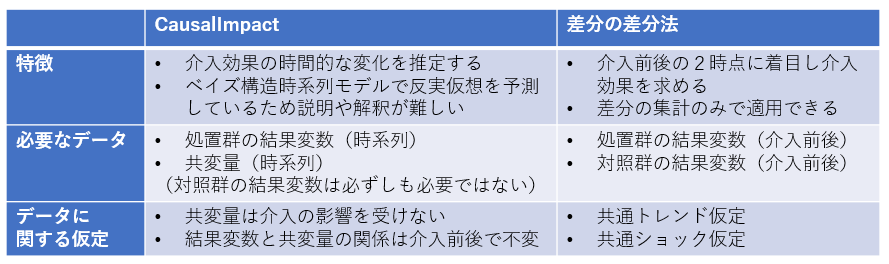
CausalImpactと、1節でも触れた差分の差分法は、いずれも施策実施前後のデータを活用することで施策の効果を検証する手法です。ここでは、差分の差分法との比較を通して、CausalImpactの特徴を詳しく見ていきます。
まず、差分の差分法は、施策の対象となる顧客などの集団（処置群）の施策実施前後の結果変数の差分と、施策の対象ではない顧客などの集団（対照群）の施策実施前後の結果変数の差分をそれぞれ計算し、それらの差分を施策の効果と見做す手法です。最初の差分で施策実施前後の結果変数の変化を捉え、次の差分で処置群と対照群の質的な違い（結果変数に影響を与える施策以外の要因）を差し引くイメージです。差分の差分法を適用するには、処置群および対照群の結果変数の実績データを取得する必要があります。もっともシンプルな差分の差分法は、特に統計モデルや機械学習モデルを導入することなく、差分の集計のみで効果検証を行うことができ、結果の解釈や説明がしやすいという特徴があります。一方で、平行トレンド仮定（時間変化による影響が処置群と対照群で同じ）や、共通ショック仮定（施策以外のイベントが与える影響が処置群と対照群で同じ）が成立している必要がありますが、効果検証に利用するデータがこれらの仮定を満たしているかを定量的に議論することが難しいという課題があります。
CausalImpactは、反実仮想を予測するモデルを構築するため、差分の差分法よりは結果の解釈や説明は難しくなりますが、施策の効果の時間的な変化を捉えられることが大きな違いです。また、反実仮想の予測が可能であれば必ずしも対照群の結果変数の実績データは必要ではなく、全顧客を対象に施策を実施した場合など、対照群のデータが得られない場合でも適用できるという利点があります。ただし、反実仮想の予測に用いる共変量は施策の影響を受けず、施策実施前後で結果変数との関係が変わらないという前提を置くため、採用する共変量は慎重に検討する必要があります。
図５：CausalImpactと差分の差分法の比較
4.2. 注意点
最後に、CausalImpactを利用して効果検証を実施する際の注意点を簡単に説明します。
まず、効果を検証したい施策と同じタイミングで、結果変数に影響を与える他のイベントが発生したり、モデルの構造が変化（たとえば、結果変数と共変量の関係性が変化）したりした場合は、施策の効果を正しく推定することが難しくなります。したがって、そのようなイベントが発生していなかったかを確認したうえでCausalImpactを利用することをお勧めします。
また、CausalImpactはパッケージを利用することで簡単に介入効果を推定し可視化することができますが、予測精度（介入効果の推定結果の妥当性）は担保していません。特に、施策開始後の反実仮想の予測値は正解データが存在しないため注意が必要です。この点については、正解データが存在する施策実施前のデータを利用し、予測精度を検証することが落としどころになるでしょう。施策実施前の（つまり、施策を実施しない場合の）結果変数を精度よく予測できていれば、施策実施後の反実仮想も精度よく予測できているだろうという仮定をおくわけです。具体的には、一般的な機械学習モデルの開発ワークフローのように、施策実施前のデータを学習用と精度検証用に分割し、モデルの構築・精度検証を行います。ただし、CausalImpactのパッケージには予測精度を検証する関数は含まれていないため、そのためのコードは別途用意する必要があります。
5. まとめ
今回は効果検証の手法として、CausalImpactを紹介しました。本記事が施策の効果検証の実務に携わる方々のご参考になれば幸いです。