1. はじめに
以前の記事では、ビジネスにおける施策の効果検証の方法として、差分の差分法という因果推論の手法について紹介しました。今回の記事では、もう1つの因果推論の手法である、傾向スコアによる分析法を紹介します。
参考文献1でも取り上げられているシチュエーションを考えてみましょう。あるスマホゲームの大手会社が、アプリの利用を促進するため、自社スマホゲームのTVCMを2週間放送しました。TVCM放送終了後、TVCMによってアプリの利用状況がどの程度改善したかを測るにはどのような検証をすればよいでしょうか。
単純には、TVCM放送後のアプリ利用状況のデータを用い、「TVCMを見たユーザーのアプリ利用時間」と「TVCMを見なかったユーザーのアプリ利用時間」の差分を計算し、これをTVCM施策の効果と見做す方法が考えられます。しかし、TVCMを見たユーザーと見なかったユーザーでは、年齢層や生活スタイルが異なるため、先程の差分にはTVCMを見たかどうか以外の要因による影響が含まれ、TVCM施策の効果をうまく推定できない場合があります。例えば、若い人のTV離れを考えると、TVを見るのは年齢層が比較的高い人たちであると予想ができ、そのような人たちは元々スマホゲームの利用時間は比較的少ないかもしれません(図1)。
このような状況で、TVCMを見たユーザーのアプリ利用時間と、見なかったユーザーのアプリ利用時間の単純な差分をとってしまうと、本来推定したい施策効果とは異なる量を推定してしまう恐れがあります。このような問題を、セレクションバイアス(選択バイアス)といいます。
今回紹介する傾向スコアを用いた分析法は、TVCMを見たユーザー層と見なかったユーザー層の属性・行動などの背景情報の違いを考慮し、施策効果をより精緻に推定するための手法です。次節では、傾向スコアを用いた分析法を解説するための準備として、因果推論の基本事項を説明します。
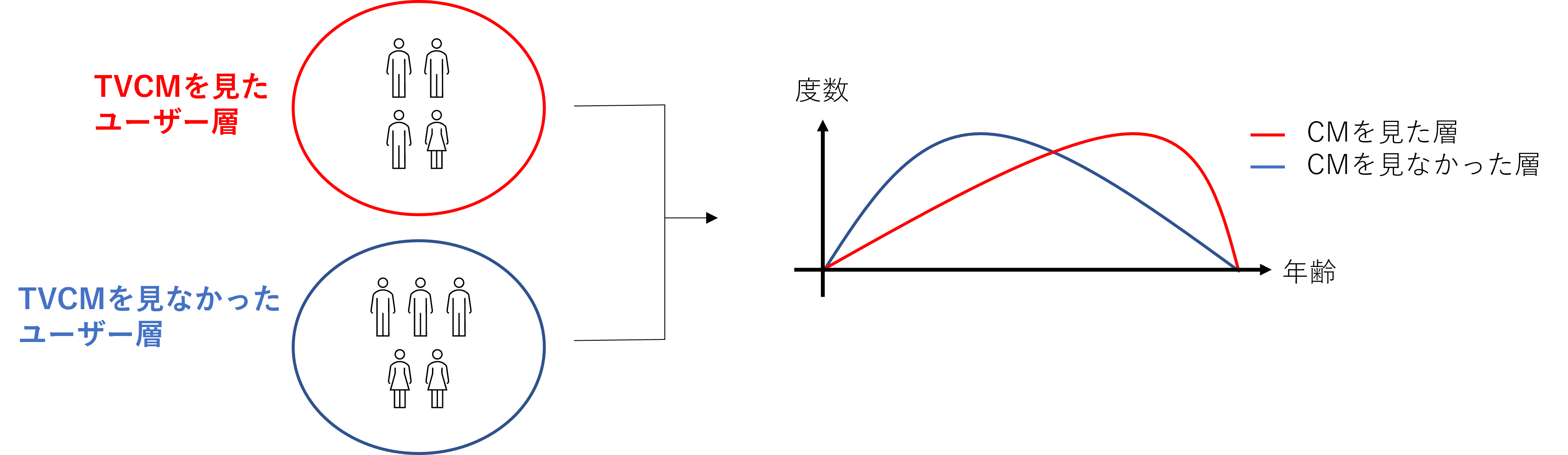
図1: TVCMをみたユーザー層と見なかったユーザー層の違い
2. 因果推論の基本事項
2-1. 用語の定義
ここでは、因果推論の用語を定義します。
まず、ユーザーにTVCMを見てもらうなどの施策やアクションのことを処置と呼びます。そして、処置を行ったユーザーのグループを処置群、処置を行わなかったユーザーのグループを対照群といいます。さらに、アプリ利用時間のような、ビジネスにおいて結果となる変数を結果変数と呼びます。ユーザー$i$ごとに処置割り当て変数$Z_i (i=1,…,N)$を導入し、ユーザー$i$が処置を受けた場合は$Z_i=1$、処置を受けなかった場合は$Z_i=0$と割り振ります。次に、各ユーザーの処置を受けた場合の結果変数を$Y_i^{(1)}$、処置を受けなかった場合の結果変数を$Y_i^{(0)}$とします。
各ユーザーに$Y_i^{(1)}$と$Y_i^{(0)}$の両方を定義することは違和感があるかもしれません。実際に観測できる結果変数は、処置群(例:TVCMを見たユーザー層)については$Y_i^{(1)}$(例:TVCMを見た場合のアプリ利用時間)のみ、対照群(例:TVCMを見なかったユーザー層)については$Y_i^{(0)}$(例:TVCMを見なかった場合のアプリ利用時間)のみだからです。しかし、ここでは、観測されなかったもう一方の結果変数も、存在はするけれどあくまで観測ができない、というように解釈します。このように、実際には起こらなかった結果についても定義する枠組みをルービンの因果モデルと呼びます。あるいは、実際には起こらなかった潜在的な結果を仮想的に考えることから、反実仮想モデルとも呼びます。
この枠組みのもとで、観測される結果変数$Y_i$を定義します。$Y_i$は、ユーザー$i$が処置群の場合は$Y_i^{(1)}$、対照群の場合は$Y_i^{(0)}$の値を取ります。したがって、$Y_i$は以下のように表すことができます。
Y_i = \left\{
\begin{array}{ll}
Y_i^{(1)} & (Z_i = 1) \\
Y_i^{(0)} & (Z_i = 0)
\end{array}
\right.
\tag{1}
最後に、共変量$X_i$を定義します。共変量$X_i$は処置割り当て変数$Z_i$と結果変数$Y_i^{(1)}$, $Y_i^{(0)}$の両方に影響を及ぼす変数のことです。今回のシチュエーションでは、年齢やTVの視聴時間などが共変量として考えられます。
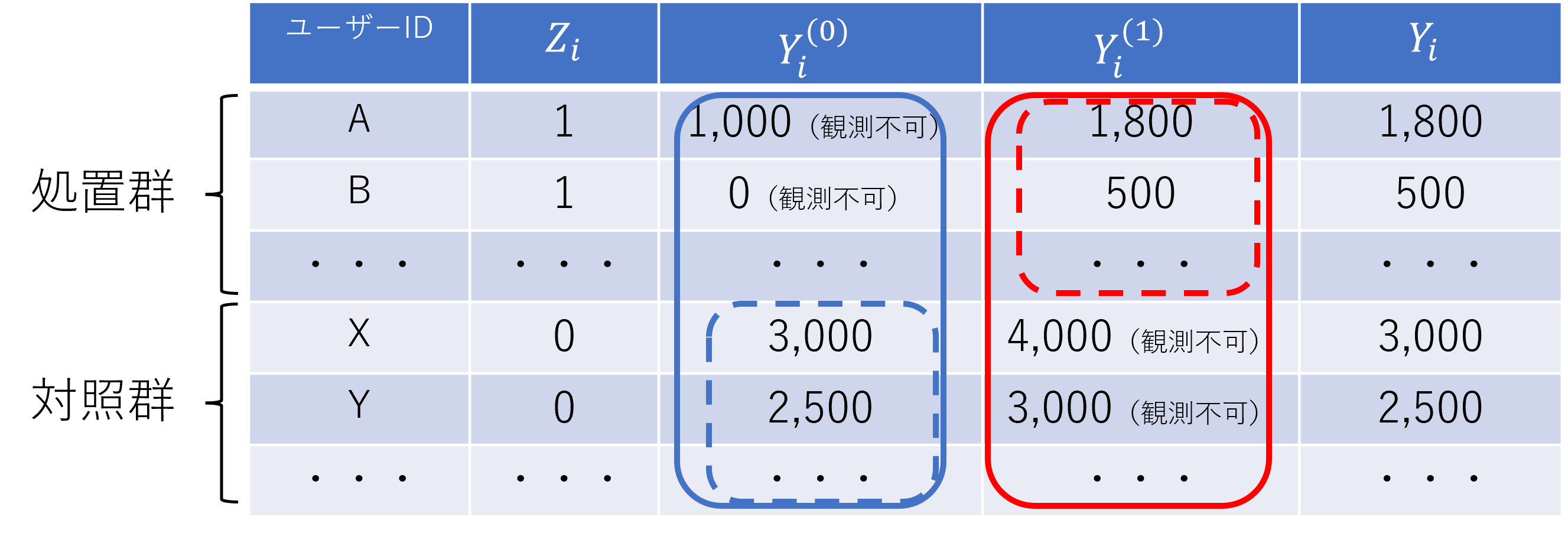
以上で定義した処置割り当て変数$Z_i$、結果変数$Y_i^{(1)}$, $Y_i^{(0)}$、および観測された結果変数$Y_i$のデータ例を表1に示します。この表では、処置群に割り当てられたユーザーは、対照群に割り当てられたユーザーに比べて結果変数$Y_i^{(1)}$, $Y_i^{(0)}$が小さい傾向にある(そもそもアプリの利用時間が短い傾向にある)という設定にしています。以降では、この表を用いて、施策の効果(処置効果)を定義していきます。
表1: 処理割り当て変数$Z_i$、結果変数$Y_i^{(1)}$, $Y_i^{(0)}$、および観測された結果変数$Y_i$の例
(結果変数$Y$はアプリ利用時間(秒)としています)
2-2. 平均処置効果(ATE)の定義
処置効果としてまず考えられるのは、以下で定義される平均処置効果(Average Treatment Effect, 以下ATE)です。
\tau_{ATE} = E[Y^{(1)}] - E[Y^{(0)}]
ATEは、各ユーザーの結果変数$Y_i^{(1)}$(例:TVCMを見た場合のアプリ利用時間)と結果変数$Y_i^{(0)}$(例:TVCMを見なかった場合のアプリ利用時間)のそれぞれの期待値の差分として定義されます。
理想的には、$\tau_{ATE}$の推定値$\hat\tau_{ATE}$は各ユーザー個人の$Y_i^{(1)}$, $Y_i^{(0)}$を用いて
\hat{\tau}_{ATE} = \frac{1}{N} \sum_{i=1}^{N}Y_i^{(1)} - \frac{1}{N} \sum_{i=1}^{N}Y_i^{(0)}
として計算することができます。第一項および第二項はそれぞれ表1の赤色の実線、および青色の実線で囲った部分の平均値に相当します。しかし、前説で説明したように、各ユーザーに対しては$Y_i^{(1)}$か$Y_i^{(0)}$のどちらかしか観測できないため、上記の計算はできません。そこで、観測されたデータのみからでも$\tau_{ATE}$を推定するために用いられる方法の一つが、次節で紹介する、傾向スコアを用いた分析法です。
ここで、少し脇道にそれますが、1節で紹介した単純な差分の集計ではどのような値を推定していることになるか、見てみましょう。(傾向スコアを用いた分析法にご興味がある方は、次節まで読み飛ばしていただいて構いません。)1節で紹介した方法では、$E[Y^{(1)}]$は処置群($Z_i=1$)から得られた$Y_i^{(1)}$のみ、$E[Y^{(0)}]$は対照群($Z_i=0$)から得られた$Y_i^{(0)}$のみを集計して算出しているので、
\hat{\tau}_{ATE}^{naive} = \frac{1}{N_1} \sum_{i=1}^{N}Z_i Y_i^{(1)} - \frac{1}{N_0} \sum_{i=1}^{N}(1 - Z_i) Y_i^{(0)}
\tag{2}
と表すことができます。ここで、$N_1=\sum_{i=1}^N {Z_i}$ は処置群のユーザー数、$N_0=\sum_{i=1}^N(1-Z_i)$は対照群のユーザー数です。これは、それぞれ表1の赤色の点線と青色の点線で囲った部分の平均値の差分を表しています。式(2)右辺の第一項は、処置群に限定した$Y_i^{(1)}$の期待値($Z=1$で条件付けた$Y_i^{(1)}$の期待値$E[Y_i^{(1)}|Z=1]$)の推定量、第二項は対照群に限定した$Y_i^{(0)}$の期待値($Z=0$で条件付けた$Y_i^{(0)}$の期待値$E[Y_i^{(0)} |Z=0]$)の推定量となっています。つまり、$\tau ̂_{ATE}^{naive}$は$E[Y_i^{(1)}|Z=1]-E[Y_i^{(0)}|Z=0]$の推定量となってしまっています。
表1を見ると、処置群($Z=1$)には対照群($Z=0$)と比べ$Y_i^{(1)}$と$Y_i^{(0)}$が小さいユーザーが多く、結果として、$\tau ̂_{ATE}^{naive}$は本来推定したい量$\tau_{ATE}$から乖離してしまうことが見て取れます。
3. 傾向スコアを用いた平均処置効果(ATE)の推定
3-1. 傾向スコアとは
傾向スコアとは、あるサンプルの共変量$X$が与えられたときの、そのサンプルが処置群に割り当てられる確率です。つまり、傾向スコア$e$は
e = Pr(Z=1|X)
と定義されます。TVCM施策の効果検証の例でいうと、年齢層が高く、TV視聴時間が長いユーザーは、処置を受ける(TVCMを見る)可能性が高く、傾向スコアは大きくなりやすいというイメージです。A/Bテストを実施する場合のように、ユーザーのグループを処置群と対照群に半々にランダムに分ける場合は、傾向スコアは$e=0.5$となります。しかし、傾向スコアの真の値は基本的に事前にはわからないため、実務上は傾向スコアの値を推定する必要があります。具体的には、$Z$を目的変数、$X$を説明変数とするモデルを作成し、そのモデルが算出する確率$Pr(Z=1|X)$を傾向スコアの推定値として用います。
3-2. 傾向スコアに求められる性質
傾向スコアを用いた分析では、傾向スコアに関して以下の性質が成り立つことを仮定している点に注意が必要です。実際にこれらの性質が成り立つためには、「強く無視できる割り当て条件」などのいくつかの条件が必要です。詳細は参考文献の3や4などをご参照ください。
- 性質1(処置割り当てと共変量の条件付き独立性)
Z \perp X|e
この性質は、傾向スコア$e$の値が等しいサンプルだけを集めたとき、処置群($Z=1$)でも対照群($Z=0$)でも共変量$X$の分布は同じということを表しています。つまり、
P(X|e, Z=1) = P(X|e, Z=0)
ということを表しています(図2)。
この性質から、処置群と対照群で共変量の分布が異なっていたとしても、両群の傾向スコアを揃えることで共変量の分布を等しくすることが可能になります。
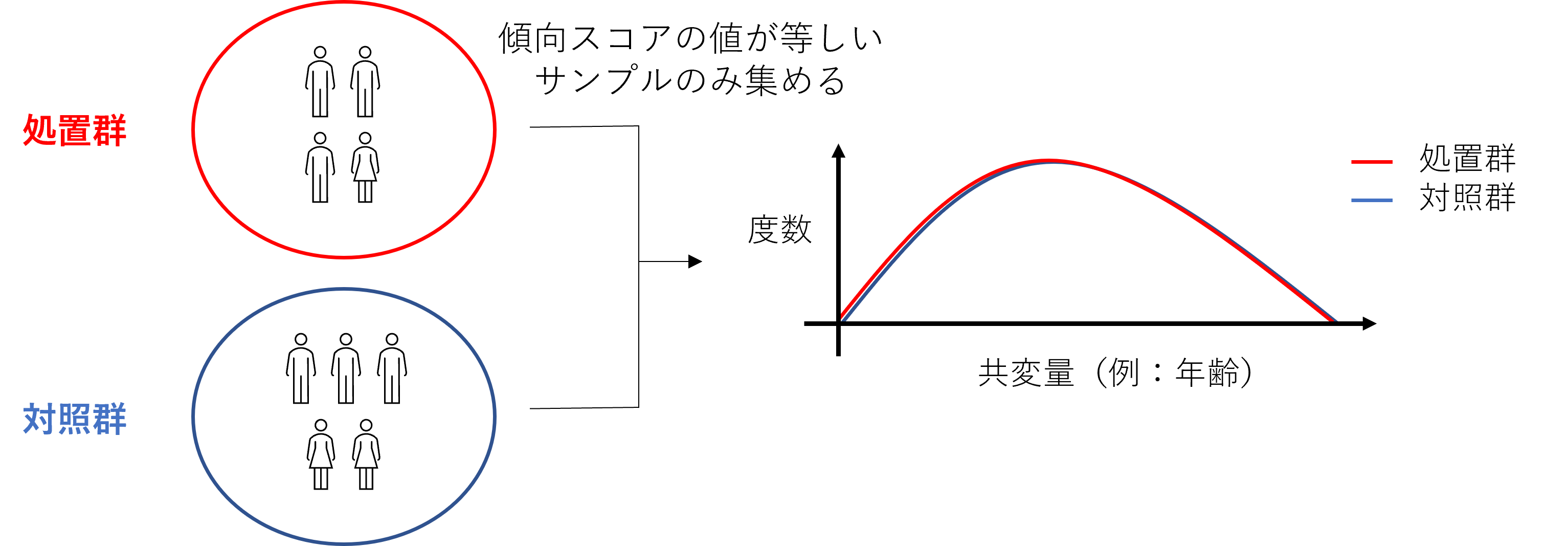
図2: 傾向スコアの性質1のイメージ
- 性質2(処置割り当てと結果変数の条件付き独立性)
Z \perp Y^{(0)}, Y^{(1)}|e
この性質は傾向スコア$e$の値が等しいサンプルだけを集めると、処置群($Z=1$)でも対照群($Z=0$)でも結果変数$Y^{(1)}$と$Y^{(0)}$の分布は同じということを表しています。つまり、
P(Y^{(1)}|e, Z=1) = P(Y^{(1)}|e, Z=0)\\
P(Y^{(0)}|e, Z=1) = P(Y^{(0)}|e, Z=0)
ということを表しています(図3)。

図3: 傾向スコアの性質2のイメージ
3-3. 逆確率重み付け法(IPW法)
傾向スコアを用いてATE($\tau_{ATE}=E[Y^{(1)}]-E[Y^{(0)}]$)を推定する方法の一つが、逆確率重み付け(Inverse Probability Weighting, IPW)法です。IPW法では、以下の式の通りATEを推定します。
\hat{\tau}_{ATE}^{IPW} = \frac{1}{N'_1} \sum_{i=1}^{N}w_{i}^{(1)}Y_i - \frac{1}{N'_0} \sum_{i=1}^{N}w_{i}^{(0)}Y_i
\tag{3}
ここで、$w_i^{(1)}=\frac{Z_i}{e_i}$、$w_i^{(0)}=\frac{1-Z_i}{1-e_i}$、$N_1^{'}=\sum_{i=1}^N w_i^{(1)}$、$N_0^{'}=\sum_{i=1}^N w_i^{(0)}$です。第一項は$E[Y^{(1)}]$の不偏推定量になっており、第二項は$E[Y^{(0)}]$の不偏推定量になっていることが、傾向スコアの性質2を用いて示すことができます。(より詳しい説明は参考文献3を参照してください。)
具体的な計算手順を見ていきます。第一項は、処置群($Z=1$)のサンプルに対して、傾向スコアの逆数($1/e_i$)で重み付けした$Y_i$の期待値を計算しています。つまり、傾向スコアが$e_i$のサンプルは$1/e_i$人分として$Y_i$を足し合わせ、重み付けにより増加した集計上のサンプル数$N'_1$で割っています。これにより、傾向スコアが大きなサンプルの重みを小さく、傾向スコアが小さなサンプルの重みを大きくしたうえで、結果変数$Y_i$の平均を計算しています。第二項も同様に、対照群($Z=0$)のサンプルに対して、$1/(1-e_i)$で重み付けした$Y_i$の期待値を計算しています。
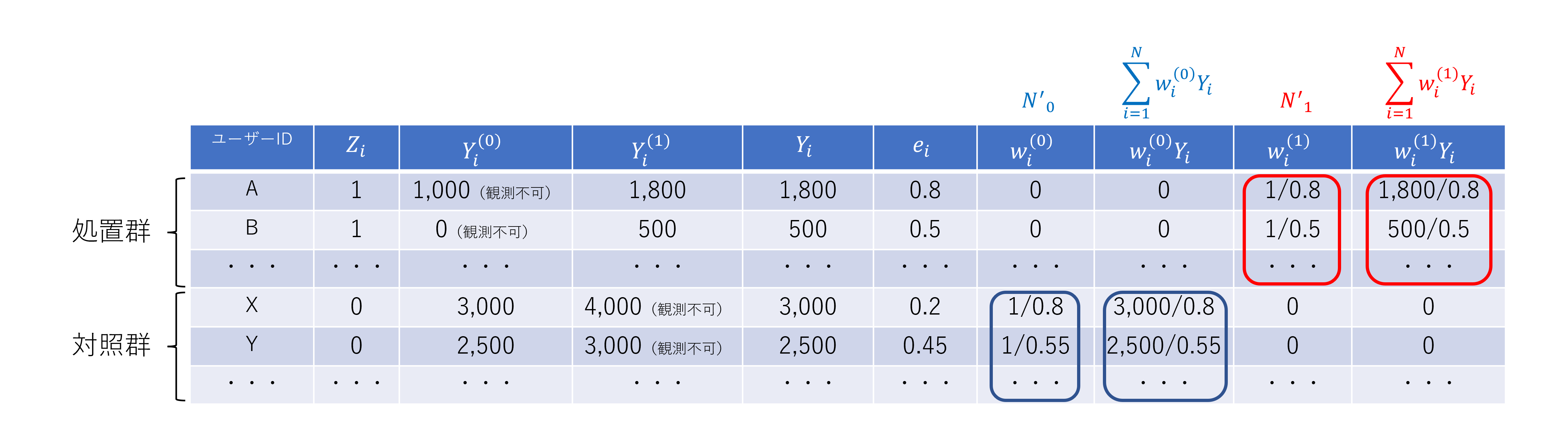
表1のデータに傾向スコア$e_i$、処置群に対する重み$w_i^{(1)}$、処置群の重み付けした結果変数$w_i^{(1)} Y_i$、対照群に対する重み$w_i^{(0)}$、対照群の重み付けした結果変数$w_i^{(0)} Y_i$を追加したものを表2に示しました。赤線部分の計算から式(3)の第一項が、青線部分の計算から式(3)の第二項を求めることができます。
3-4. IPW法のイメージ
ここまでIPW法の計算式を説明しましたが、ここではIPW法をもっと嚙み砕いたイメージを説明します。
TVCM施策の効果検証の例では、年齢層が高く、TV視聴時間が長いユーザーは、処置を受ける(TVCMを見る)可能性が高く、傾向スコアが大きくなりやすい状況を考えました。このように、ユーザーを処置群と対照群のいずれかに明示的に割り当てられない状況では、処置群と対照群で傾向スコアの分布は異なる場合が多いです。傾向スコアが同じ$e$の値をとるサンプルを集めてきたとき、傾向スコアの定義から、そのうちの$e$の割合のサンプルが処置群に、残りの$1-e$の割合のサンプルが対照群に割り当てられていることになります。例えば、傾向スコアが0.1程度のサンプルが1,000人いたとき、約100人が処置群に、残りの約900人が対照群に割り当てられることになります。つまり、傾向スコアが大きなサンプルは処置群に偏り、傾向スコアが小さいサンプルは対照群に偏ることになります(図4)。
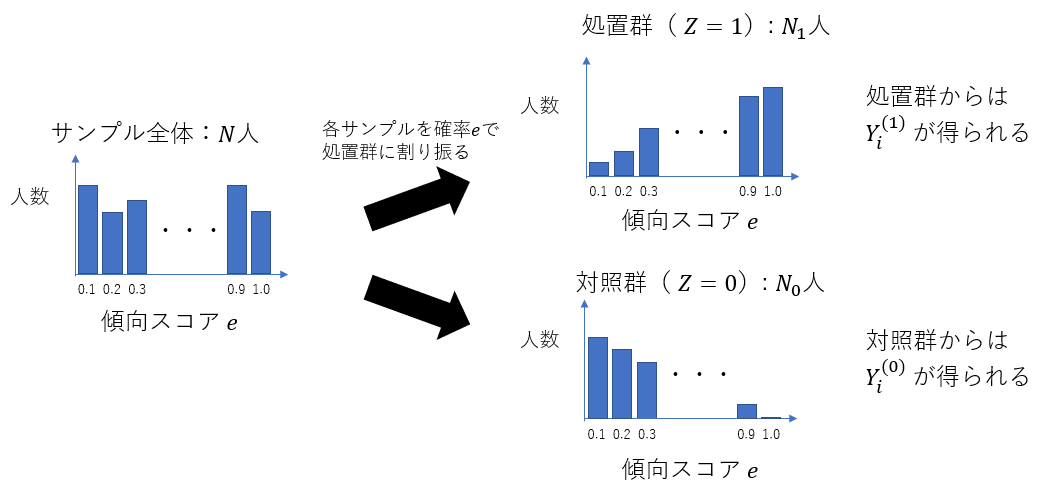
図4: サンプル全体・処置群・対照群における傾向スコアの分布
IPW法では、処置群・対照群における傾向スコアの分布の偏りを補正しています。
まず、式(3)第一項で$E[Y^{(1)}]$を推定する際に、処置群($Z_i=1$)のサンプルの$Y_i$を傾向スコアの逆数$1/e_i$で重み付けすることで、サンプル全体における傾向スコアの分布にもとづく$Y^{(1)}$の期待値を推定しています。同様に、第二項で$E[Y^{(0)}]$を推定する際に、対照群($Z_i=0$)のサンプルの$Y_i$を$1/(1-e_i)$ で重み付けすることで、サンプル全体における傾向スコアの分布にもとづく$Y^{(0)}$の期待値を推定しています(図5)。
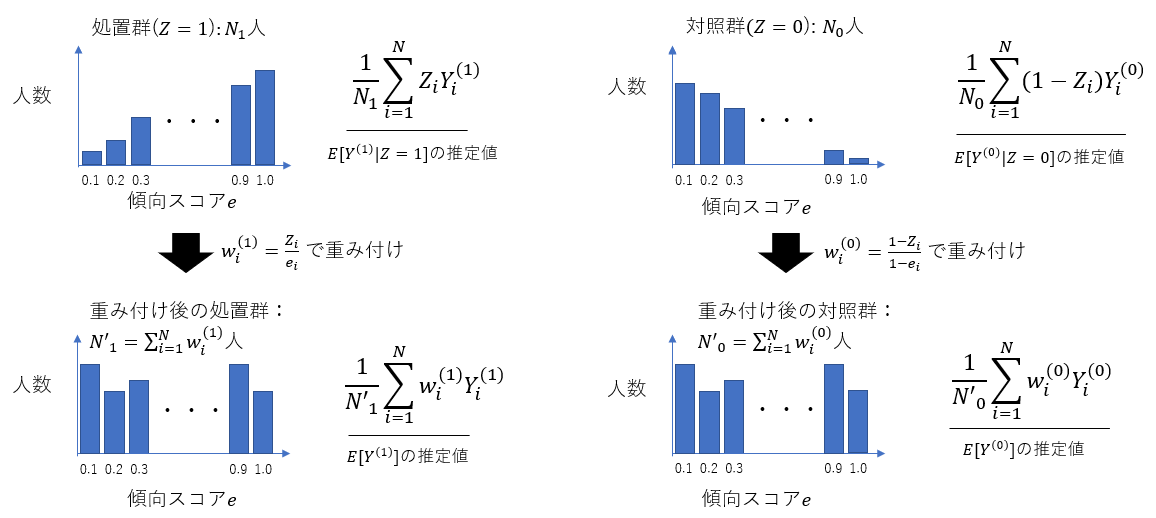
図5: IPW法によるATE推定のイメージ
そして、傾向スコアの性質1を踏まえると、IPW法は処置群と対照群における傾向スコアの分布を揃えることで、補正後の処置群と対照群の共変量の分布も揃えていることになります(図6)。これにより、処置群のユーザーと対照群のユーザーの属性・行動の違いに起因するセレクションバイアスの影響を軽減し、より精緻にATEを推定することができます。
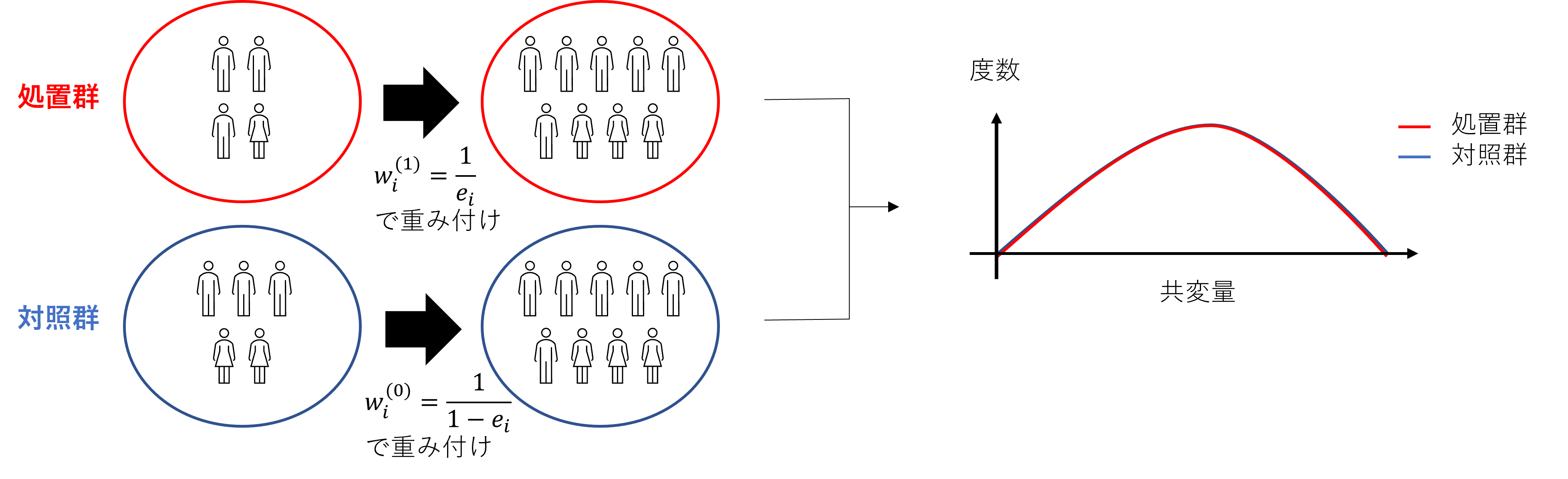
図6: 傾向スコアによる補正後の処置群と対照群の共変量の分布(ATEを推定する場合)
4. 処置群に対する処置効果(ATT)の推定
これまでは、サンプル全体に対する平均的な処置効果であるATEを考えてきました。一方で、処置群に対する平均処置効果(Average Treatment Effect on the Treated, ATT)を考えることが有効な場合もあります。
例えば、TVCM施策を実施したときにどれほど効果があったのか、その費用対効果を検証する際には、実際にTVCMを見たユーザー(処置群)に限定した処置効果を測定するほうが適切でしょう。本節では、ATTの定義およびIPW法を用いてATTを推定する方法について説明します。
4-1. ATTの定義
ATTは、以下の式の通り、結果変数$Y_i^{(1)}$と$Y_i^{(0)}$の処置群に限定した($Z=1$の条件付き)期待値の差分として定義されます。
\tau_{ATT} = E[Y^{(1)}|Z=1] - E[Y^{(0)}|Z=1]
理想的には、処置群($Z_i=1$)における結果変数$Y^{(1)}$, $Y^{(0)}$を用いてATTを推定することができます。
\hat{\tau}_{ATT} = \frac{1}{N_1} \sum_{i=1}^{N} Z_iY_i^{(1)} - \frac{1}{N_1} \sum_{i=1}^{N} Z_iY_i^{(0)}
\tag{4}
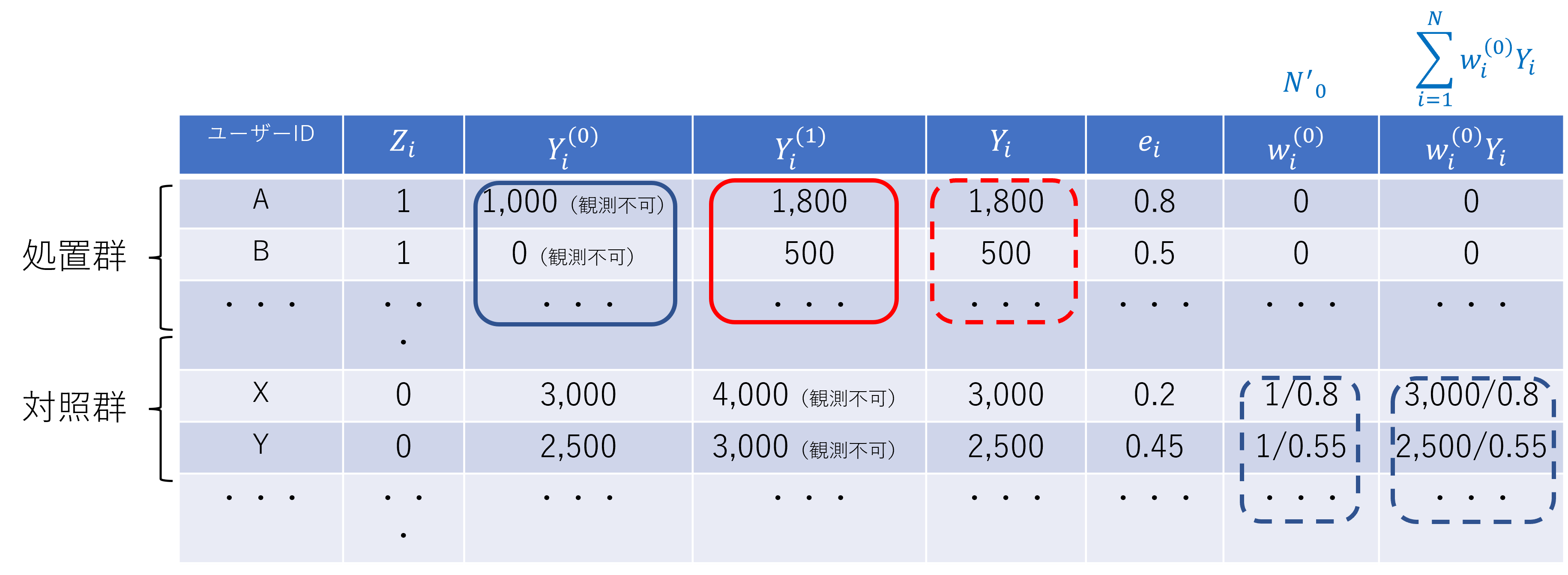
式(4)の計算のイメージを示すために、表2のデータ例を一部抜粋したものを表3に示します。式(4)第一項および第二項は、それぞれ赤色の実線および青色の実線で囲った部分の平均値に相当します。式(4)第一項は、処置群における結果変数$Y^{(1)}$(処置を受けた場合の結果変数)の平均値であるため、観測されたデータから計算することができます。しかし、式(4)第二項は処置群における結果変数$Y^{(0)}$(処置を受けなかった場合の結果変数)の平均値であり、観測されたデータからは計算できません。そこで、傾向スコアを用いてこれを推定することを考えます。
4-2. IPW法によるATTの推定方法
処置群に対する平均処置効果(ATT)も、傾向スコアによる重み付け(IPW)を活用することで推定することができます。
\hat{\tau}_{ATT}^{IPW} = \frac{1}{N_i} \sum_{i=1}^{N} Z_iY_i - \frac{1}{N_0^{ATT}} \sum_{i=1}^{N} w_i^{\prime(0)}Y_i
\tag{5}
ここで、$w_i^{\prime(0)}=\frac{(1-Z_i)e_{i}}{1-e_i}$、$N_0^{ATT}=\sum_{i=1}^{N}w_i^{\prime(0)}$です。式(5)第一項は、処置群($Z_i=1$)から観測された結果変数$Y_i$の平均値です。式(5)第二項は、対照群のサンプル($Z=0$)に対して、$e_i/(1-e_i)$で重み付けした$Y_i^{(0)}$の平均値を計算しています。言い換えると、対照群のサンプルを$e_i/(1-e_i)$人分として、$Y_i^{(0)}$を足し合わせ、重み付けにより変化した集計上のサンプル数に相当する$N_0^{ATT}$で割っています(表3の青色の点線で囲った部分の計算)。$e_i/(1-e_i)$は$e_i$に比例して大きくなるため、傾向スコアが大きなサンプルの重みは大きく、傾向スコアが小さなサンプルの重みは小さくなります。つまり、対照群のサンプルの中でも、傾向スコア、つまり処置群への割り当て確率がより大きなサンプルを重視して結果変数を集計しています。
4-3. IPW法によるATTの推定イメージ
ATTを推定する場合、式(5)は、対照群における傾向スコアの分布の偏りを補正しています。すなわち、対照群における傾向スコアの分布を、処置群における傾向スコアの分布に揃えています(図7)。対照群は傾向スコア、つまり処置群に割り当てられる確率が低いサンプルが多いため、$1/(1-e_i)$倍してサンプル全体の傾向スコアの分布に合わせ、さらに$e_i$倍することで処置群における傾向スコアの分布に合わせにいくイメージです。
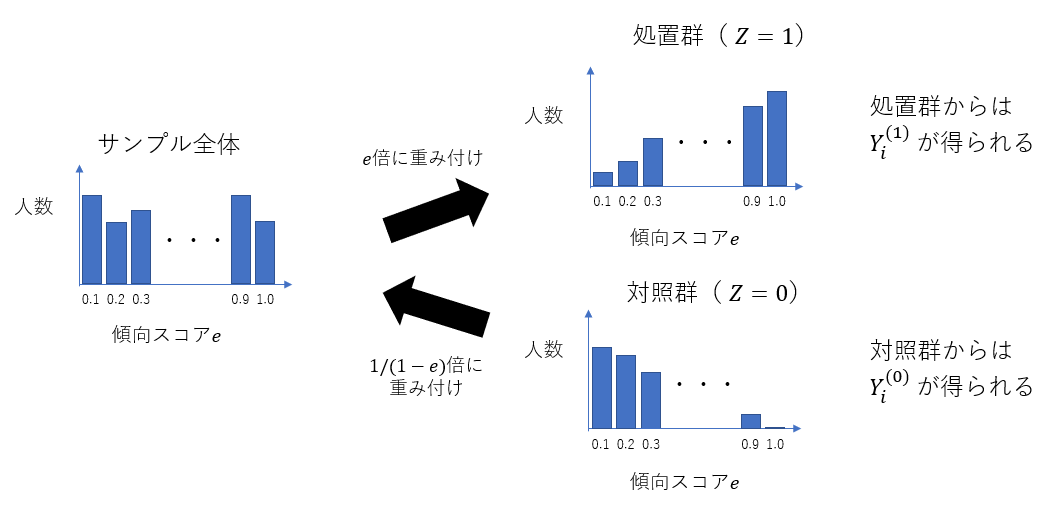
図7: 対照群の傾向スコア分布の補正イメージ
ATTを推定する際は、$E[Y^{(0)}|Z=1]$を推定するために、式(5)第二項のように対照群($Z_i=0$)のサンプルの$Y_i^{(0)}$を$e_i/(1-e_i)$で重み付けすることで、処置群における傾向スコアの分布にもとづく$Y^{(0)}$の期待値を推定しています(図8)。
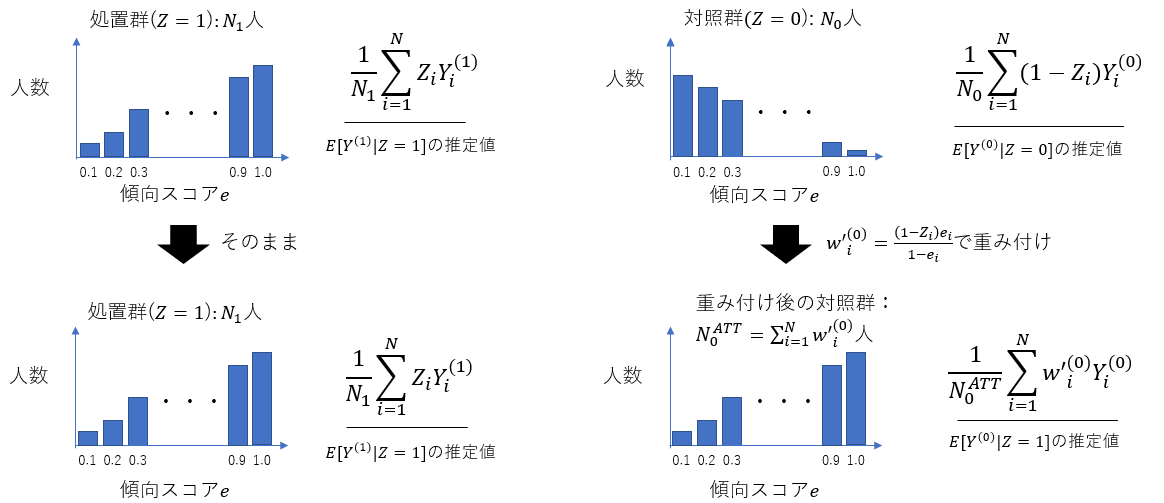
図8: IPW法によるATT推定のイメージ
また、傾向スコアの性質1を踏まえると、処置群と対照群における傾向スコアの分布を揃えることで、補正後の処置群と対照群の共変量の分布も揃えています。特にこの場合は、対照群における共変量の分布を、処置群における共変量の分布に揃えています(図9)。これにより、処置群のユーザーが、処置を受けることによってどれだけ結果変数が変化したかをより精緻に捉えることができます。
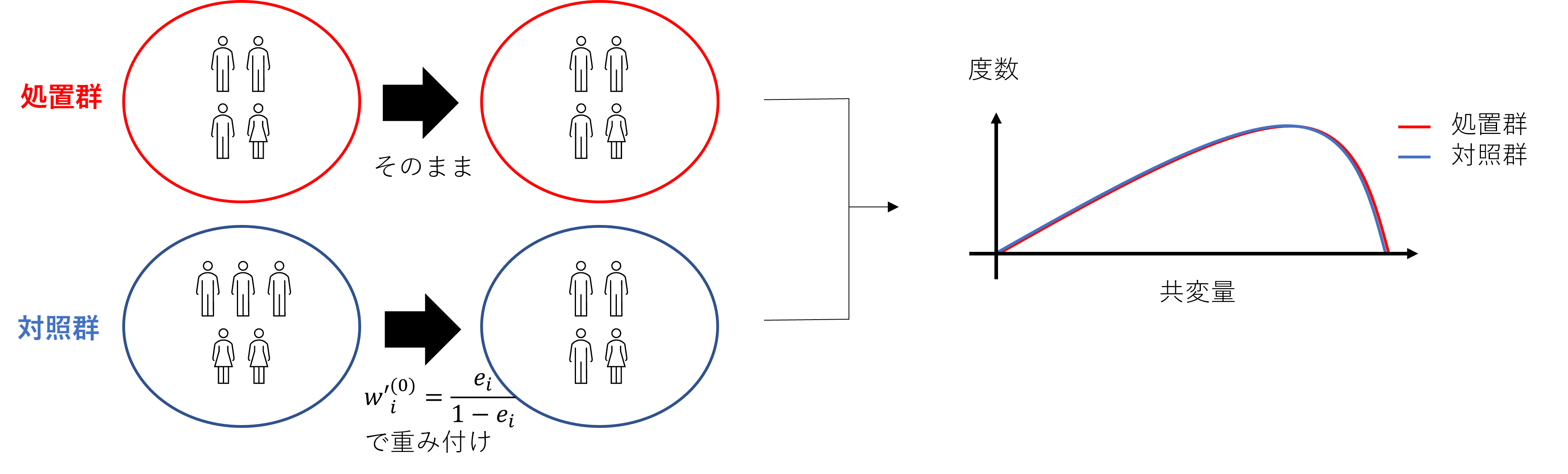
図9: 傾向スコアによる補正後の処置群と対照群の共変量の分布(ATTを推定する場合)
5. 補足:セレクションバイアスの可視化
この節では、平均処置効果(ATE)を単純な集計によって推定した値$\tau ̂_{ATE}^{naive}$と真の値$\tau_{ATE}$との差(セレクションバイアス)について、傾向スコアを用いて可視化する方法を説明します。特に、傾向スコアと結果変数に正と負どちらの相関があるかによってバイアスの方向(単純な差分の集計が過大推定となるか、あるいは過小推定となるか)が変わることを見ます。
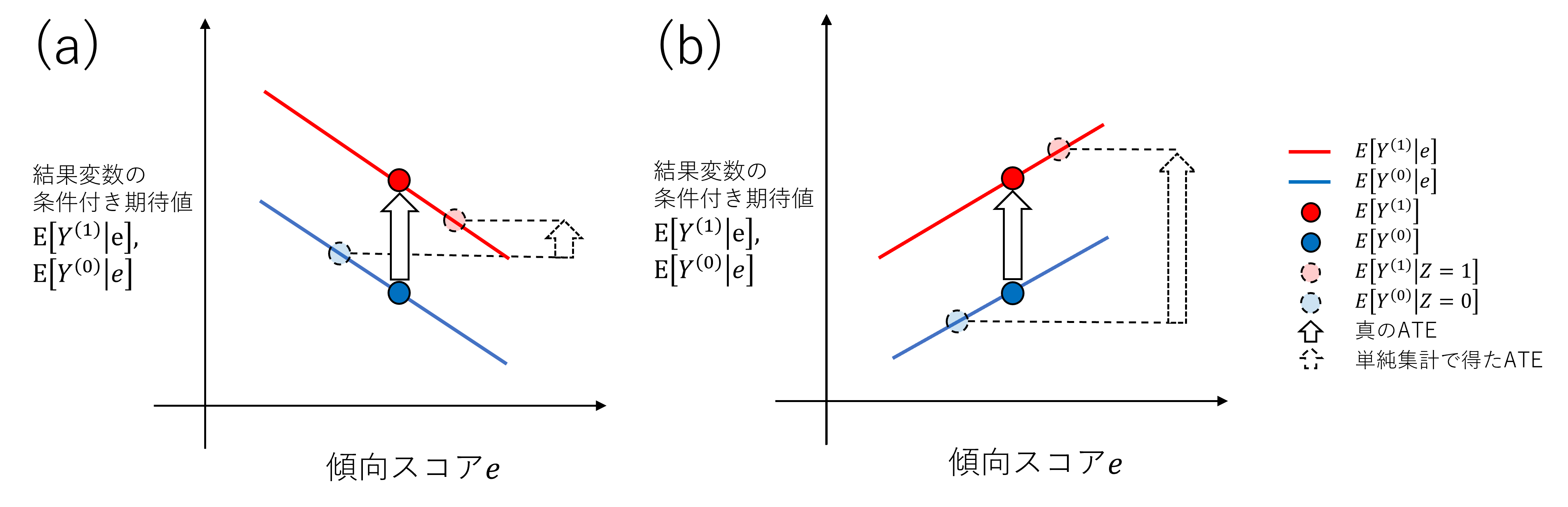
まず、傾向スコア$e$と結果変数$Y^{(1)}$, $Y^{(0)}$に負の相関がある、つまり、処置群に割り当てられやすいサンプルのほうが結果変数が小さい傾向がある場合について考えます。TVCM施策の効果検証の例のように、傾向スコアが高いサンプル(TVCMを見る可能性が高いユーザー)ほど結果変数が小さい(アプリ利用時間が短い)ような状況がこの場合に相当します。簡単のため、傾向スコア$e$に対して結果変数の期待値$E[Y^{(1)}|e]$, $E[Y^{(0)}|e]$が線形に減少する状況を考えます(図10(a))。
この状況で、ATEの単純な集計による推定値$\tau ̂_{ATE}^{naive}$を可視化してみます。2-2.で説明したように、$\tau ̂_{ATE}^{naive}$は$E[Y_i^{(1)}|Z=1]-E[Y_i^{(0)}|Z=0]$の推定量です。処置群($Z=1$)は傾向スコアが比較的大きい集団であることを踏まえると、第一項の$E[Y^{(1)}|Z=1]$は、図10(a)の$E[Y^{(1)}|e]$のグラフの右側の値を取ります。一方で、対照群($Z=0$)は傾向スコアが比較的小さい集団となるため、第二項の$E[Y^{(0)}|Z=0]$は、図10(a)の$E[Y^{(0)}|e]$のグラフの左側の値を取ります。したがって、$\tau ̂_{ATE}^{naive}$は図10(a)右側の短い矢印で示すことができます。
次に、ATEの真の値$\tau_{ATE}$の可視化を行います。$\tau_{ATE}$は$E[Y^{(1)}]-E[Y^{(0)}]$と定義されます。処置群と対照群を合わせたサンプル全体は、傾向スコアが中間程度の集団となるので、$E[Y^{(1)}]$と$E[Y^{(0)}]$はそれぞれ図10(a)の$E[Y^{(1)}|e]$と$E[Y^{(0)}|e]$のグラフのほぼ中央の値を取ります。したがって、$\tau_{ATE}$は図10(a)中央の矢印で表すことができます。二つの矢印の長さ、すなわち$\tau ̂_{ATE}^{naive}$と$\tau_{ATE}$の大きさをと比べると、前者のほうが矢印は短く、小さい値を取ることになります。つまり、単純な集計による推定は過小推定になります。
次に、傾向スコア$e$と結果変数$Y^{(1)}$, $Y^{(0)}$に正の相関がある、つまり、処置群に割り当てられやすいサンプルのほうが結果変数が大きい傾向がある場合を考えます(図10(b))。図10(a)の場合と同様に$\tau ̂_{ATE}^{naive}$と$\tau_{ATE}$を可視化すると、$\tau ̂_{ATE}^{naive}$は図10(b)右側の長い矢印で示すことができ、$\tau_{ATE}$は図10(b)中央の矢印で表すことができます。二つの矢印の長さを比べると、$\tau ̂_{ATE}^{naive}$は$\tau_{ATE}$より大きい値を取り、単純な集計による推定は過大推定になることが見て取れます。
以上のように可視化を行うことで、単純な集計によって効果検証を行った場合のセレクションバイアスの方向がわかりやすくなります。
実際のデータ分析においても、図10の縦軸と横軸の値を推定値に置き換えて可視化をすると、効果検証の分析方針について何かヒントが得られるかもしれません。
6. まとめ
今回は、効果検証の手法として、傾向スコアによる分析法を紹介しました。本記事が施策の効果検証の実務に携わる方々のご参考になれば幸いです。