ヒープソートの理解

ソートアルゴリズムには、選択ソート、挿入ソート、マージソート、バブルソート、ヒープソートなどがあるが、その中で最も理解に苦しんだヒープソートをPythonで整理していく。

ヒープとは

ヒープソートに用いられるヒープは木構造であり、子ノードの値は、親ノードの値以上である性質を持つ。この場合、ルートの値は最小値になり、最小値の探索が簡単になる。逆に、子ノードの値が親ノードの値以下の場合もあり、ルートの値は最大値になる。親ノードが最大２つの子ノードを持つ構成を二分ヒープ木という。

##ヒープソートの実装
子ノードの値が親ノードの値以上の場合で実装していく。
二分ヒープ木をリストで構成する時、ある位置のインデックス番号が0の場合、左の子ノードのインデックス番号は1、右の子ノードのインデックス番号は2になる。つまり、ある位置のインデックス番号がnの場合、左の子ノードのインデックス番号は2n + 1、右の子ノードのインデックス番号は2n + 2になる。また、親ノードは(n - 1) // 2になる。

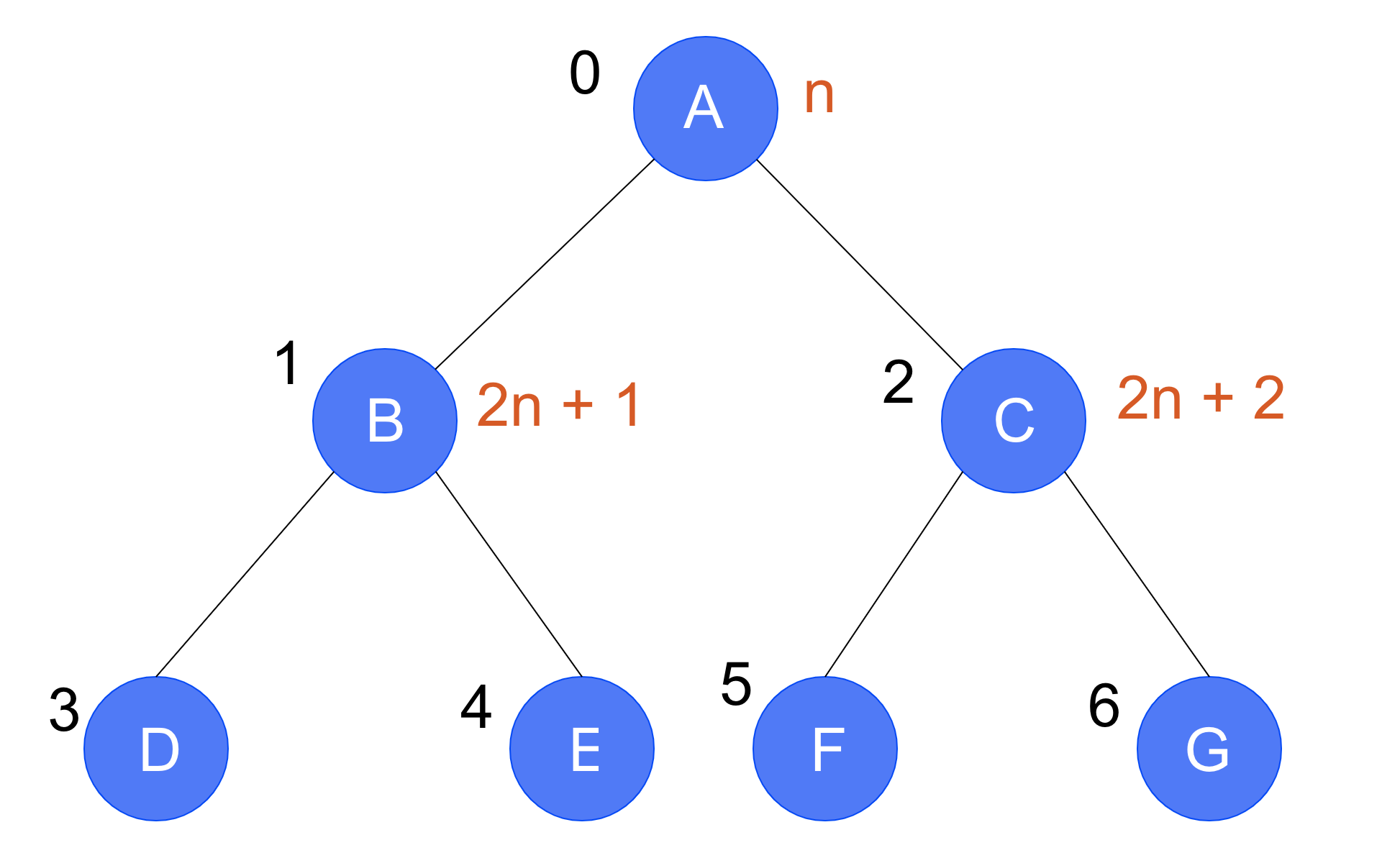
ヒープを構成

数字がまばらに格納されるリストを昇順にソートしていく。
リスト（[3,6,1,4,8,2]）があり、そのリストでヒープを構成する。現在の位置がルートでない、または値が親より大きい間は、親と交換し、位置を親の位置に移動する。

Python

data = [3, 6, 1, 4, 8, 2]

# ヒープを構成
for i in range(len(data)):
    pos = i
    # 現在の位置がルートでない、または値が親より大きい間は、親と交換し、位置を親の位置に移動
    while (pos > 0) and (data[(pos - 1) // 2] < data[pos]):
        data[(pos - 1) // 2], data[pos] = data[pos], data[(pos - 1) // 2]
        pos = (pos - 1) // 2
        print(data)

実行結果

[6, 3, 1, 4, 8, 2]
[6, 4, 1, 3, 8, 2]
[6, 8, 1, 3, 4, 2]
[8, 6, 1, 3, 4, 2]
[8, 6, 2, 3, 4, 1]
[8, 6, 2, 3, 4, 1]

ヒープソートを実行

現在の位置の値をヒープの先頭と交換する。左下の値の方が大きい場合、左下と交換し、右下の値の方が大きい場合、右下と交換する。これを繰り返していくとリストの値が昇順にソートされる。

Python

for i in range(len(data), 0, -1):
    data[i - 1], data[0], = data[0], data[i - 1]
    # ヒープの先頭から開始
    pos = 0
    while ((pos * 2 + 1 < i - 1) and (data[pos] < data[pos * 2 + 1])) or (
        (pos * 2 + 2 < i - 1) and (data[pos] < data[pos * 2 + 2])):
        # 左下の値の方が大きい場合、左下と交換
        if (pos * 2 + 2 == i - 1) or (data[pos * 2 + 1] > data[pos * 2 + 2]):
            data[pos], data[pos * 2 + 1] = data[pos * 2 + 1], data[pos]
            pos = pos * 2 + 1
        # 右下の値の方が大きい場合、右下と交換
        else:
            data[pos], data[pos * 2 + 2] = data[pos * 2 + 2], data[pos]
            pos = pos * 2 + 2
        print(data)

print(data)

実行結果

[6, 1, 2, 3, 4, 8]
[6, 4, 2, 3, 1, 8]
[4, 1, 2, 3, 6, 8]
[4, 3, 2, 1, 6, 8]
[3, 1, 2, 4, 6, 8]
[1, 2, 3, 4, 6, 8]

最後に

ヒープソートにはupheapやdownheapも存在するが、今回は省略。
まだあやふやなところがあるので、何度も見直して理解を深めたい。
間違い等があればご指摘お願いいたします。

参考

増井 敏克「Pythonではじめるアルゴリズム入門 伝統的なアルゴリズムで学ぶ定石と計算量」 翔泳社 ２０２０年１月２４日