言語モデルが足し算の概念を理解できるのか確かめようとした

はじめに

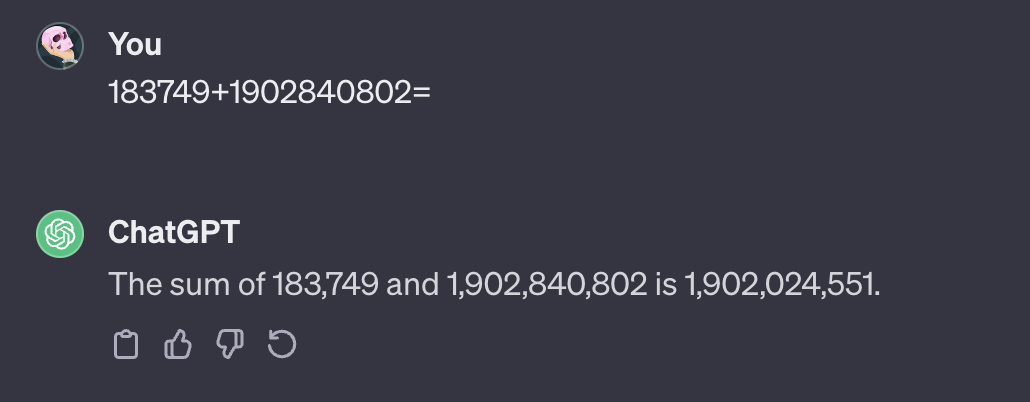
言語モデルは計算が苦手だとよく言われます．事実ChatGPT(gpt3.5-turbo)でも以下のように桁数の多い足し算をやらせると計算ミスをしてしまっています．

電卓を叩いてみれば気づきますが，本当の答えは1903024551であり百万の桁が異なります．

以上の知見と大量のテキストデータを学習するという言語モデルの学習方法から，言語モデルは暗記的思考でテキストを吐いている，逆に言語モデルから発せられるテキストはどこかに転がっているものである可能性が高いと考えるのが普通です．

上記のように作られたものを検証しているのはよく見ますが，一から学習させて言語モデルに足し算という概念を理解できるのか，自分の手で動かしてその可能性を確かめたいと思いました．

なお用いた実験コードは github で公開しています．

対象者

• NLP研究に興味のある人
• 言語モデルの能力に興味のある人

どのように確かめるか

厳密な条件設定をして調査することは自分には難しいと考えたので簡易的な実験をしてみてその可能性を探ろうと思います．
具体的にはまず言語モデルにGPTアーキテクチャをもつ小さめのモデルであるgpt2をhuggingfaceのGPT2LMHeadModelクラスにて学習しました．

使用したテキスト

学習データには以下のような2つの数字の足し算で左辺が両方とも1以上50以下，右辺が99以下となるものを用いました．

学習データ

\displaylines{
1 + 1 = 2 \\
1 + 2 = 3 \\
\vdots \\
1 + 50 = 51 \\
2 + 1 = 3 \\
2 + 2 = 4 \\
\vdots \\
50 + 49 = 99
}

逆にテストデータには以下のような左辺どちらかが51以上98以下，右辺が99以下となるものを用いました．テストするときは左辺から右辺を予測します．

テストデータ

\displaylines{
1 + 51 = 52 \\
1 + 52 = 53 \\
\vdots \\
1 + 98 = 99 \\
2 + 51 = 53 \\
2 + 52 = 54 \\
\vdots \\
48 + 51 = 99
}

こうすることで，学習データの右辺に1から99まですべての数字が現れ，足し算の概念，数字の大小を学習データから理解できれば，テストデータを予測することができるはずです．
また今回は桁数は制限しましたが，上記の2桁の計算の他に3桁の計算でも実験をしてみました(付録参照)．
このほかの方法(数式をランダムに選ぶ，桁数の制限をしないなど)でも結果は変わってくると思うので，それらは気が向いたらやろうと思います．

tokenizer

数式のtoken分割には数字ごとの場合と，桁ごとの場合との2通りでtokenizerを自作して試しました．

数字ごとの場合のtokenizer

N = 100
MAX_LEN = 6
def tokenizer_bynumber(p, q, type):
    """ pとqから 'p+q=r' という数式を作って数字ごとにtokenizeする関数 引数typeにはこのデータが訓練用か検証用か('train' or 'valid' or 'test') """
    text_input_ids = np.full_like(np.zeros([MAX_LEN], dtype=np.int64), N)
    target_input_ids = np.full_like(np.zeros([MAX_LEN], dtype=np.int64), N)
    text_attention_mask = np.zeros([MAX_LEN], dtype=np.int64)

    text_input_ids[0], text_input_ids[1], text_input_ids[2], text_input_ids[3], text_input_ids[4], text_input_ids[5] = p, N+2, q, N+3, p+q, N+1
    target_input_ids[0], target_input_ids[1], target_input_ids[2], target_input_ids[3], target_input_ids[4], target_input_ids[5] = -100, -100, -100, -100, p+q, N+1
    """特殊token_id{ pad:N, eos:N+1, +:N+2, =:N+3 }"""
    text_attention_mask[0], text_attention_mask[1], text_attention_mask[2], text_attention_mask[3], text_attention_mask[4], text_attention_mask[5] = 1, 1, 1, 1, 1, 1
    if type == "valid" or type == "test":
        text_input_ids = np.delete(text_input_ids, [-1, -2])
        target_input_ids = text_input_ids
        text_attention_mask = np.delete(text_attention_mask, [-1, -2])

    text_input_ids = torch.from_numpy(text_input_ids).clone()
    target_input_ids = torch.from_numpy(target_input_ids).clone()
    text_attention_mask = torch.from_numpy(text_attention_mask).clone()

    tokenized_inputs = {"input_ids":text_input_ids,"attention_mask":text_attention_mask}
    tokenized_targets = {"input_ids":target_input_ids,"attention_mask":text_attention_mask}

    return tokenized_inputs, tokenized_targets 

$27+34=61$を入れた場合，input_idsは

tensor([ 27, 102,  34, 103,  61, 101])

となる．（'+'のidが102，'='のidが103，101はeos_token_id）

桁ごとの場合のtokenizer

N = 100
MAX_LEN = 16
def tokenizer_bydigit(p, q, type):
    """ pとqから 'p+q=r' という数式を作って桁ごとにtokenizeする関数 引数typeにはこのデータが訓練用か検証用か('train' or 'valid' or 'test') """
    text_input_ids = np.full_like(np.zeros([MAX_LEN], dtype=np.int64), N)
    target_input_ids = np.full_like(np.zeros([MAX_LEN], dtype=np.int64), N)
    text_attention_mask = np.zeros([MAX_LEN], dtype=np.int64)
    p, q, r = [i for i in str(p)], [i for i in str(q)], [i for i in str(p+q)]
    j = -1
    if type == "train":
        text_input_ids[j], target_input_ids[j], text_attention_mask[j] = N+1, N+1, 1
        j -= 1
        for i_idx, i in enumerate(r):
            text_input_ids[j], target_input_ids[j], text_attention_mask[j] = int(r[-i_idx-1]), int(r[-i_idx-1]), 1
            j -= 1
    text_input_ids[j], target_input_ids[j], text_attention_mask[j] = N+3, -100, 1
    j -= 1
    for i_idx, i in enumerate(q):
        text_input_ids[j], target_input_ids[j], text_attention_mask[j] = int(q[-i_idx-1]), -100, 1
        j -= 1
    text_input_ids[j], target_input_ids[j], text_attention_mask[j] = N+2, -100, 1
    j -= 1
    for i_idx, i in enumerate(p):
        text_input_ids[j], target_input_ids[j], text_attention_mask[j] = int(p[-i_idx-1]), -100, 1
        j -= 1
    """特殊token_id{ pad:N, eos:N+1, +:N+2, =:N+3 }"""

    text_input_ids = torch.from_numpy(text_input_ids).clone()
    target_input_ids = torch.from_numpy(target_input_ids).clone()
    text_attention_mask = torch.from_numpy(text_attention_mask).clone()

    tokenized_inputs = {"input_ids":text_input_ids,"attention_mask":text_attention_mask}
    tokenized_targets = {"input_ids":target_input_ids,"attention_mask":text_attention_mask}

    return tokenized_inputs, tokenized_targets 

$27+34=61$を入れた場合，input_idsは

tensor([100, 100, 100, 100, 100, 100, 100,   2,   7, 102,   3,   4, 103,   6,
          1, 101])

となる．（'+'のidが102，'='のidが103，101はeos_token_id，100はpad_token_id）

結果

2桁同士の計算での学習データとテストデータの精度は以下のようになりました．

学習データ精度(数字ごとにtoken分割)

────────────────────────────────────────────────────────────────────────────────────────
        train_acc           0.9927971363067627
────────────────────────────────────────────────────────────────────────────────────────

テストデータ精度(数字ごとにtoken分割)

────────────────────────────────────────────────────────────────────────────────────────
        test_acc                    0.0
────────────────────────────────────────────────────────────────────────────────────────

試しに以下のデータで推論

• $27+43=61$ (学習データ)
• $63+24=87$ (テストデータ)
• $7+84=91$ (テストデータ)

数字ごとにtoken分割したモデルの推論結果

predicted:27+34=61, answer:27+34=61
predicted:63+24=69, answer:63+24=87
predicted:7+84=15, answer:7+84=91

学習データ精度(桁ごとにtoken分割)

────────────────────────────────────────────────────────────────────────────────────────
        train_acc          0.012805121950805187
────────────────────────────────────────────────────────────────────────────────────────

テストデータ精度(桁ごとにtoken分割)

────────────────────────────────────────────────────────────────────────────────────────
        test_acc          0.0008503401186317205
────────────────────────────────────────────────────────────────────────────────────────

試しに推論

桁ごとにtoken分割したモデルの推論結果

predicted:27+34=6007874, answer:27+34=61
predicted:63+24=690744281, answer:63+24=87
predicted:7+84=71, answer:7+84=91

どちらもテストデータでは精度が上がらず...

おわりに

言語モデルの計算能力のその一端を調べるためにこのような実験を行ってみました！
結果はテストデータでほぼ0%となってしまいました．．．
テストデータはもちろんのこと，桁ごと分割の実験ではそもそも学習データですら100%には程遠い結果となりました．おおよそ言語モデルが計算を苦手としていることを実感できた気がします．
パラメータの調節や学習モデルのサイズを大きくするなどによって精度の改善はするかもしれません．しかし完全に足し算の概念を理解するのは難しそうです...
この実験を人間が同じように学習したら間違えることはないと思うので，人間の数理的思考と言語モデルの根幹は別物かもしれないとすら思ってしまいました...

今回はgpt2を自作tokenizerを用いて訓練しました．計算能力を調べる目的以外でもこのような実験が役に立てばと思います！冒頭にも記しましたが実験コードは github にて公開しています．

なお本記事が初投稿でした．ご指摘やアイデアおまちしています！

参考文献

Teaching Arithmetic to Small Transformers
https://arxiv.org/abs/2307.03381
四則演算を用いた Transformer の再帰的構造把握能力の調査
https://www.anlp.jp/proceedings/annual_meeting/2022/pdf_dir/A4-5.pdf
(12/21追記)以下の記事でデータ作成など異なる点はありますが時系列モデルで同じような実験をしているものがありました．記事の結果からデコーダモデルではなくてエンコーダ・デコーダモデルでも試してみたいと思いました．
https://qiita.com/chama0623/items/b6648bc7b998b955d24a

付録

3桁計算での結果も以下に載せておきます．

学習データ精度(数字ごとにtoken分割，3桁計算)

────────────────────────────────────────────────────────────────────────────────────────
        train_acc           0.8296433091163635
────────────────────────────────────────────────────────────────────────────────────────

テストデータ精度(数字ごとにtoken分割，3桁計算)

────────────────────────────────────────────────────────────────────────────────────────
        test_acc          4.828934834222309e-05
────────────────────────────────────────────────────────────────────────────────────────

学習データ精度(桁ごとにtoken分割，3桁計算)

────────────────────────────────────────────────────────────────────────────────────────
        train_acc          0.0001320005248999223
────────────────────────────────────────────────────────────────────────────────────────

テストデータ精度(桁ごとにtoken分割，3桁計算)

────────────────────────────────────────────────────────────────────────────────────────
        test_acc         2.8168788048787974e-05
────────────────────────────────────────────────────────────────────────────────────────