概要

時系列分析と自然言語処理の勉強のアウトプットとして, kerasで実装したSeq2Seqを用いて足し算を学習してみました. 足し算の学習とは文字列"123+45"を入力すると"168"が出力されるような学習のことを指します. ソースコードはほぼkerasのCode ExampleのものですがGithubにも載せてあります.

実行環境

ホストがWindows11のDocker環境
CPU AMD Ryzen 5 3600
メモリ 16GB
GPU NVIDIA GeForce RTX 2060
Python 3.8.10
Numpy 1.22.2
matplotlib 3.5.1
tensorflow 2.8.0
keras 2.8.0

学習アルゴリズム

学習アルゴリズムとして, Recurrent Neural Network(RNN), Long Short-Term Memory(LSTM), Sequence to Sequence(Seq2Seq)とそのテクニックの4つについて簡単に紹介します. しっかり理解したい方は参考文献をご覧ください.

Recurrent Neural Network(RNN)

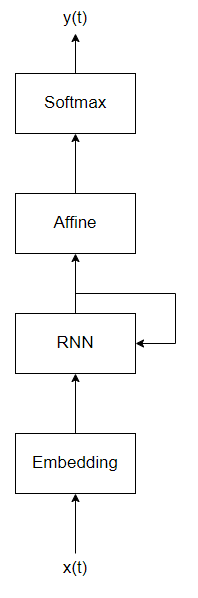
Neural Networkは入力層から隠れ層へ, 隠れ層から出力層へ信号が伝わる, 一方向の信号伝達を行うネットワークでした. このように一方向だけに信号を伝達するようなネットワークをフィードフォワードネットワークといいます. フィードフォワードネットワークは時系列データをうまく扱うことができません. これは時系列データは前のデータと次のデータに関係をもつものがあるため, 一方向にのみ信号伝達を行う構造では時系列の関係を学習することができないためです. そこでRecurrent Neural Network(RNN)という循環する構造を持つニューラルネットワークが考えられました. RNNは次のような構造です.

最大の特徴はRNNレイヤの出力がRNNレイヤに再び入力されていることです. 時刻$t-1$のRNNレイヤの出力$h_{t-1}$とすると, 時刻$t$ではEmbeddingレイヤの出力と$h_{t-1}$(ひとつ前の時刻の出力)が入力されます¹. このように循環する構造を持つためRNNは時系列データに対してうまく学習することができます. RNNレイヤやEmbeddingレイヤの内部構造はここでは説明しませんが気になる方は参考文献1をご覧ください.
RNNの簡単な例としてsin波の推測があります. 直前までのいくつかのsin波の値が与えられて次の値がいくつになるのか予測することができます.

Long Short-Term Memory(LSTM)

RNNには時系列データの長期間の依存関係をうまく学習できないという問題点があります. この問題はRNNの学習の際に過去方向に伝わっていく勾配が消失・爆発が起きてしまうために発生します.² 勾配消失を解決するためにRNNレイヤに改良を加えたモデルがLong Short-Term Memory(LSTM)です.³ 具体的には過去の情報を記憶する/忘れることをゲートで制御することで勾配消失が起こりにくいようにしています. RNNレイヤとLSTMレイヤの違いを簡単に説明すると次の図のようになります. LSTMでは隠れ状態$h_t$に加えて記憶セル$c_t$が追加されます. 記憶セル$c_t$は情報を記憶する役割があります. LSTM内部のゲート構造や計算については説明を省略しますがこちらも面白いので参考文献1をご覧ください.

Seq2Seq

Seq2Seqは機械翻訳を行うモデルです. 機械翻訳はGoogle翻訳やDeepLをイメージするととても分かりやすいです. 例としては日本語「大きいことはいいことだ」を英語「big is good」に訳すような処理を行うモデルです. Seq2Seqは次に示すようにEncoderとDecoderから構成されています.

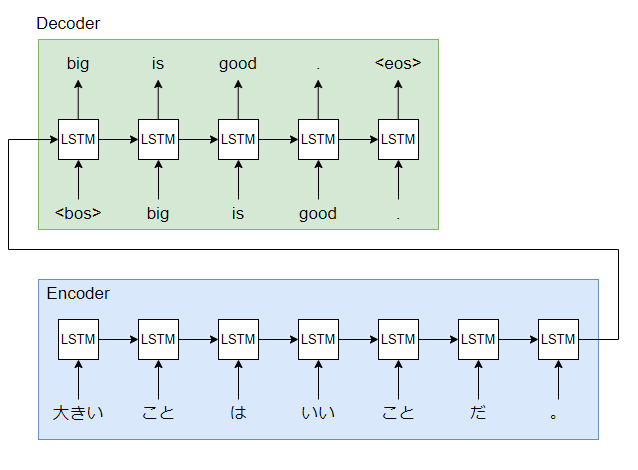
日本語から英語に翻訳する例では形態素解析等の前処理をした文をEncoderに入力するとEncoderの隠れ状態ベクトルが出力されます. 最終的な隠れ状態ベクトルをDecoderの隠れ状態ベクトルとして入力すると英語に翻訳された文が出力されます. <bos>は文の始まり(begin of sentence), <eos>は文の終わり(end of sentence)を表します. Seq2SeqはEncoderとDecoderの2つのRNNを用いて機械翻訳を実現しています.

Seq2Seqのテクニック1 Reverse

Seq2Seqモデルの精度を向上させるテクニックとして入力を反転させるReverseがあります. 先の例では文の先頭から「大きい」「こと」「は」「いい」「こと」「だ」「。」という順番でEncoderに入力しました. Reverseの場合は文の末尾から「。」「だ」「こと」「いい」「は」「こと」「大きい」という順番で入力します. 先頭の情報を最後に伝えることで勾配が伝わりやすくなるためReverseを行うことで精度を向上させることができます.

Seq2Seqのテクニック2 Peeky

Encoderの出力hにはDecoderに必要な情報が詰まっています. 出力hをDecoderの最初だけでなく時間展開したLSTMレイヤとAffineレイヤに入力して隠れ状態を覗き見る(peeky)テクニックを行うことで, Encoderからの情報をより活用してSeq2Seqの性能を向上させることができます.

製作物のイメージ

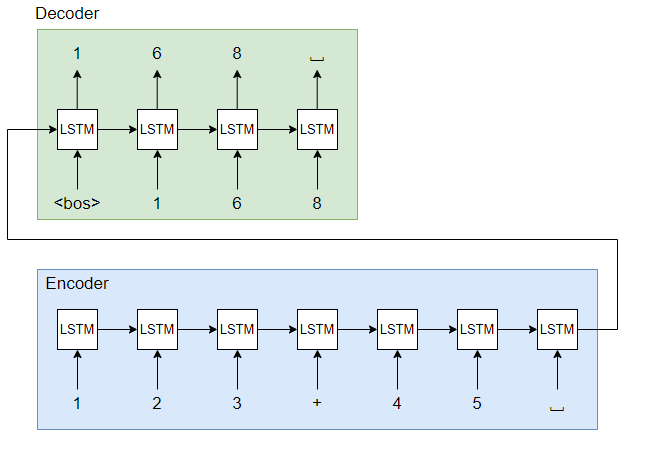
Seq2Seqで足し算を学習させるイメージを説明します. Seq2Seqの構造と入出力データの例は次のようになります. ここでは最大3桁+最大3桁を考えます. つまり入力される文字列の最大の長さは「3桁 + プラス記号(+) + 3桁」の7文字になります. 出力される文字列は3桁+3桁の和だから4桁が最大になります. 値がないときは空白(スペース)でパディングします.

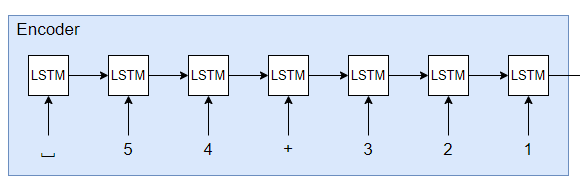
Reverseを用いるときは入力文字列を反転します. すなわち"123+45"のEncoderの入力は次のようになります. 最後に数字の情報を入力することで重要な情報の勾配が伝わりやすくなることがイメージできます. このようにしてSeq2Seqで足し算を行うモデルを実装します.

プログラムと実行結果

実装したプログラムと実行結果について説明します. プログラムはkerasのCode Exampleを参考にしました.

ライブラリ読み込み

まず, numpyとmatplotlibを読み込みます.

import numpy as np
import matplotlib.pyplot as plt

データの生成

データを生成します. まず訓練データの数, 最大桁数, Reverseの有無を表す定数を定義します. 次のプログラムでは訓練データの数を50000, 最大桁数を3桁, Reverseをありに設定しています. MAXLENは入力文字列の最大の長さを表しています.

# train set size
TRAINING_SIZE = 50000
# 最大桁数
DIGITS = 3
# Reverseの有無
REVERSE = True

# 入力される文字列の最大長
MAXLEN = DIGITS + 1 + DIGITS

次にデータを生成します. 2行目のCharacterTableクラスについては後で説明します. 次のプログラムではa,b 2つの2桁以下の数字をランダムに生成して文字列"a+b"の形に変換する処理を行っています. 変換したときに文字列の長さがMAXLEN未満の場合は空白" "でパディングを行います. そして変換した文字列は["123+45 "]というようになります. REVERSEが真のときは変換した文字列を反転させます. 問題に対して処理を行って生成されたリストはquestions, 正解に対して処理を行って生成されたリストはexpectedに格納されます.

chars = "0123456789+ "
ctable = CharacterTable(chars) # インスタンス化

questions = []
expected = []
seen = set()
print("Generating data...")
while len(questions)<TRAINING_SIZE: # train size回反復
    f = lambda: int(
    "".join( # 空白文字列に足していく
    np.random.choice(list("0123456789")) # 1桁の数字を1文字選ぶ
    for i in range(np.random.randint(1,DIGITS+1)) # 1～桁数回繰り返す
    )
    )
    
    a,b = f(),f() # a,b 2つの数字を無名関数fから取得
    key = tuple(sorted((a,b)))
    if key in seen: # 2数の組み合わせが既にseenに定義されているとき
        continue
    seen.add(key)
    q = "{}+{}".format(a,b) # a+b文字列に変換
    query = q + " " * (MAXLEN - len(q)) # パディング
    ans = str(a + b) # 正解文字列
    ans +=" " *(DIGITS+1-len(ans)) # パディング
    if REVERSE: # Reverse処理
        query = query[::-1]
    questions.append(query)
    expected.append(ans)
print("Total questions:",len(questions))

実行結果
Generating data...
Total questions: 50000

正しく実行されたか確認します. Reverseが行われているため問題文が反転していますがインデックス0番の問題は739+9, 正解は748になっているため正しいことがわかります.

questions[:5],len(questions)

実行結果
([' 9+937', ' 88+7', ' 7+23', ' 36+21', ' 184+27'], 50000)

expected[:5],len(expected)

実行結果
(['748 ', '95 ', '39 ', '75 ', '553 '], 50000)

データをベクトルに変換する

データをOne-hotなベクトルに変換します. sikit-learn等を用いてone-hotなベクトルに変換しても良いですが, ここではベクトルに変換(エンコード)する処理とベクトルを文字列に戻す(デコード)する処理を行うクラスを作成します. このクラスが先ほど説明を省略したCharacterTableクラスです. CharacterTableクラスはコンストラクタの引数としてベクトルに変換する文字列が取りえる値charsを与える必要があります. メインでchars = "0123456789+ "と定義しているため0～9の数字とプラス記号(+), 空白" "が取りえる値になります.
encodeメソッドは引数Cで与えた文字列をnum_rowsの長さのone-hotなベクトルに変換します. decodeメソッドはx与えられたベクトルを文字列に変換します.

# ベクトル化するためのクラス
class CharacterTable:
    def __init__(self, chars):
        self.chars = sorted(set(chars))
        self.char_indices = dict((c, i) for i,c in enumerate(self.chars))
        self.indices_char = dict((i, c) for i,c in enumerate(self.chars))
        
    def encode(self, C, num_rows):
        x = np.zeros((num_rows, len(self.chars)))
        for i, c in enumerate(C):
            x[i, self.char_indices[c]] = 1
        return x
    
    def decode(self, x, calc_argmax=True):
        if calc_argmax:
            x = x.argmax(axis=-1)
        return "".join(self.indices_char[x] for x in x)

CharacterTableクラスを用いて文字列をベクトルに変換する処理を次に示します. このプログラムではctableインスタンスで問題と正解をそれぞれエンコードします. そしてエンコード結果の配列をシャッフルして45000を訓練セット, 5000を検証セットとして分割します.

print("Vectorization...")
x = np.zeros((len(questions),MAXLEN,len(chars)),dtype=np.bool_)
y = np.zeros((len(questions),DIGITS+1,len(chars)),dtype=np.bool_)

for i,sentence in enumerate(questions):
    x[i] = ctable.encode(sentence,MAXLEN)
for i,sentence in enumerate(expected):
    y[i] = ctable.encode(sentence,DIGITS+1)
    
indices = np.arange(len(y))
np.random.shuffle(indices)
x=x[indices]
y=y[indices]

split_at = len(x) -len(x)//10
(x_train,x_val) = x[:split_at],x[split_at:]
(y_train,y_val) = y[:split_at],y[split_at:]

print("Training Data:")
print(x_train.shape)
print(y_train.shape)

print("Validation Data:")
print(x_val.shape)
print(y_val.shape)

実行結果
Vectorization...
Training Data:
(45000, 7, 12)
(45000, 4, 12)
Validation Data:
(5000, 7, 12)
(5000, 4, 12)

エンコードした結果がone-hotなベクトルになっていることを確認しましょう.

x_train[0],y_train[0]

実行結果
(array([[False, False, False, False, False, False, False, True, False,
False, False, False],
[False, False, False, False, False, False, False, False, False,
False, True, False],
[False, False, False, False, False, True, False, False, False,
False, False, False],
[False, True, False, False, False, False, False, False, False,
False, False, False],
[False, False, False, False, False, False, False, False, False,
True, False, False],
[False, False, False, False, False, False, False, False, True,
False, False, False],
[False, False, False, False, True, False, False, False, False,
False, False, False]]),
array([[False, False, False, False, False, False, False, False, True,
False, False, False],
[False, False, False, False, False, False, False, True, False,
False, False, False],
[False, False, False, False, True, False, False, False, False,
False, False, False],
[ True, False, False, False, False, False, False, False, False,
False, False, False]]))

モデリング

ネットワークを構築します. まずkerasをimportします.

from tensorflow import keras
from tensorflow.keras import layers

ネットワーク構造や最適化関数, 誤差関数を記述します.

print("Build model...")
num_layers = 1

model = keras.Sequential()
model.add(layers.LSTM(128,input_shape=(MAXLEN,len(chars))))
model.add(layers.RepeatVector(DIGITS+1))
for _ in range(num_layers):
    model.add(layers.LSTM(128,return_sequences=True))
    
model.add(layers.Dense(len(chars),activation="softmax"))

model.compile(loss="categorical_crossentropy",optimizer="adam",metrics=["accuracy"])
print("complete")

今回作成したモデルは次のようなモデルです. RepeatVectorは時間展開したすべてのLSTMレイヤにEncoderからの隠れ状態ベクトルを入力するPeekyの役割を果たしています.

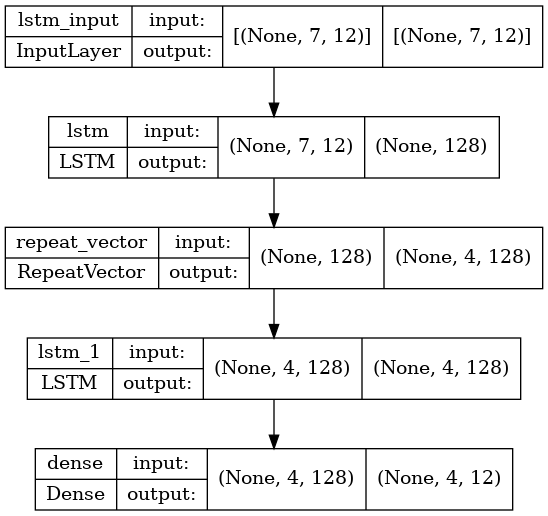
学習結果(Reverseなしの場合)

まずはReverseなしで学習を行いました. プログラムは実行が正しく行われているかの確認も踏まえて1epochs毎に検証データからランダムに数個選んだデータの予測を計算して表示させています. epochs数は30, バッチサイズは12で学習を行いました.

# Reverseなしの場合
# 学習の途中でvalidationを表示する
epochs = 30
batch_size = 12

for epoch in range(1,epochs): # 1epoch毎にvalからランダムに抜き出して精度を確認
    history = model.fit(x_train,y_train,batch_size=batch_size,epochs=1,
                       validation_data=(x_val,y_val),)

    for i in range(10):
        ind = np.random.randint(0,len(x_val))
        rowx,rowy = x_val[np.array([ind])],y_val[np.array([ind])]
        preds = np.argmax(model.predict(rowx),axis=-1)
        q = ctable.decode(rowx[0])
        correct = ctable.decode(rowy[0])
        guess = ctable.decode(preds[0],calc_argmax=False)
        print("Q", q[::-1] if REVERSE else q, end=" ")
        print("T", correct, end=" ")
        if correct == guess:
            print("〇 " + guess)
        else:
            print("× " + guess)

実行結果 (長いのでところどころ表示します)
Qは問題, Tは正解, ×または〇で表示されているものはモデルの予測結果と正誤を表します. epoch数が少ないときはほとんど正解できていませんが, 学習が進むとほぼすべての検証データに対して加算結果が正しいことがわかります.

1epoch目
3750/3750 [==============================] - 31s 7ms/step - loss: 1.6025 - accuracy: 0.4081 - val_loss: 1.2570 - val_accuracy: 0.5233
Q 45+312 T 357 × 355
Q 804+44 T 848 × 881
Q 770+531 T 1301 × 1281
Q 14+470 T 484 × 501
Q 345+95 T 440 × 431
Q 26+12 T 38 × 56
Q 53+77 T 130 〇 130
Q 45+423 T 468 × 482
Q 286+0 T 286 × 280
Q 74+20 T 94 × 10

5epoch目
3750/3750 [==============================] - 26s 7ms/step - loss: 0.2081 - accuracy: 0.9374 - val_loss: 0.1406 - val_accuracy: 0.9627
Q 443+44 T 487 〇 487
Q 597+219 T 816 〇 816
Q 263+213 T 476 〇 476
Q 803+78 T 881 〇 881
Q 693+29 T 722 〇 722
Q 81+441 T 522 〇 522
Q 982+51 T 1033 〇 1033
Q 41+324 T 365 〇 365
Q 4+100 T 104 × 103
Q 689+862 T 1551 〇 1551

10epoch目
3750/3750 [==============================] - 23s 6ms/step - loss: 0.0446 - accuracy: 0.9872 - val_loss: 0.0971 - val_accuracy: 0.9696
Q 84+952 T 1036 〇 1036
Q 72+701 T 773 〇 773
Q 77+391 T 468 〇 468
Q 1+415 T 416 〇 416
Q 74+91 T 165 〇 165
Q 681+22 T 703 〇 703
Q 2+70 T 72 〇 72
Q 402+99 T 501 〇 501
Q 94+162 T 256 〇 256
Q 965+375 T 1340 〇 1340

30epoch名
3750/3750 [==============================] - 27s 7ms/step - loss: 0.0100 - accuracy: 0.9974 - val_loss: 0.0050 - val_accuracy: 0.9988
Q 39+352 T 391 〇 391
Q 61+972 T 1033 〇 1033
Q 74+196 T 270 〇 270
Q 73+12 T 85 〇 85
Q 192+296 T 488 〇 488
Q 16+70 T 86 〇 86
Q 44+848 T 892 〇 892
Q 499+70 T 569 〇 569
Q 262+8 T 270 〇 270
Q 667+45 T 712 〇 712

学習結果(Reverseありの場合)

Reverseありのときのプログラムと実行結果を示す.

# Reverseありの場合
# 学習の途中でvalidationを表示しない
epochs = 30
batch_size = 12

history = model.fit(x_train,y_train,batch_size=batch_size,epochs=epochs,
                    validation_data=(x_val,y_val),)

def plot_loss(history):
    """エポックごとの損失関数をプロットする関数
    
    Args:
    history : fittingの履歴
    
    Returns:
    None
    """
    # 損失関数の履歴を取得
    loss_train = history.history["loss"]
    loss_val = history.history["val_loss"]

    # 損失関数をプロット
    epochs=range(1,len(history.history["loss"])+1)
    plt.figure(facecolor="white")
    plt.plot(epochs,loss_train,label="Training loss")
    plt.plot(epochs,loss_val,label="Validation loss")
    plt.legend()
    plt.xlabel('Epochs')
    plt.ylabel('Loss')
    plt.savefig("loss.jpg")
    plt.show()
    
def plot_acc(history):
    """エポックごとの正解率をプロットする関数
    
    Args:
    history : fittingの履歴
    
    Returns:
    None
    """
    acc_train = history.history['accuracy']
    acc_val = history.history['val_accuracy']
    epochs = range(1,len(history.history["accuracy"])+1)
    plt.figure(facecolor="white")
    plt.plot(epochs, acc_train, 'g', label='Training accuracy')
    plt.plot(epochs, acc_val, 'b', label='Validation accuracy')
    plt.legend()
    plt.xlabel('Epochs')
    plt.ylabel('Accuracy')
    plt.savefig("acc.jpg")
    plt.show()

# 損失関数の描画
plot_loss(history)

# 正解率を描画
plot_acc(history)

実行結果(学習ログは省略)
損失関数のグラフ

正解率のグラフ

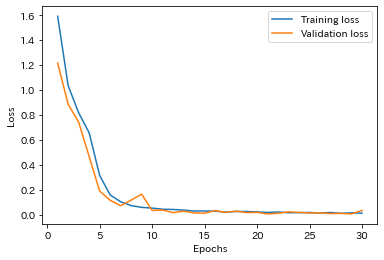
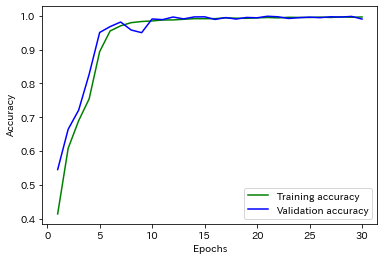
損失関数は単調に減少, 正解率は単調に増加しているため過学習は起きていないことがわかります. 30epoch目の検証データにおける正解率は0.9969でした.

推論処理の実行

最後に自由に入力した2つの数字の文字列aとbの加算結果を推論する処理を行うプログラムを次に示します.

# 好きな数字で推論
a = "123"
b = "456"
q = a+"+"+b # a+b文字列に変換
query = q + " " * (MAXLEN - len(q)) # パディング
if REVERSE: # Reverse処理
        query = query[::-1]
x_new = ctable.encode(query,MAXLEN).astype(np.bool_)
x_new = x_new.reshape(1,-1,12)
pred = np.argmax(model.predict(x_new),axis=-1)
print("predict :",ctable.decode(pred[0],calc_argmax=False))
print("correct :",int(a)+int(b))

実行結果
predict : 579
correct : 579

感想

ゼロから作るDeep Learning2で学習した内容についてKerasを用いて実装することができました. AttentionやTransformerも勉強する予定なのでそちらでも何か実装したら記事を作ろうと思います.

参考文献

斎藤康毅, ゼロから作るDeep Learning ❷ ――自然言語処理編, https://www.oreilly.co.jp/books/9784873118369/
Keras, Code examples Sequence to sequence learning for performing number addition, https://keras.io/examples/nlp/addition_rnn/
Sowmya Vajjala、Bodhisattwa Majumder、Anuj Gupta、Harshit Surana　著、中山光樹　訳, 実践自然言語処理,https://www.oreilly.co.jp/books/9784873119724/

$h_t$は隠れ状態や隠れ状態ベクトルと呼ばれます. ↩
勾配爆発の対策は勾配クリッピングという手法があります. ↩
代表的なモデルにGRUというものもあります. ↩

Seq2Seqで足し算を学習する

概要