Chainerは、Preferred Networksが開発したニューラルネットワークを実装するためのライブラリです。その特徴としては、以下のような点があります(ホームページより)。
- 高速: CUDAをサポートし、GPUを利用した高速な計算が可能
- 柔軟: 柔軟な記法により、畳み込み、リカレントなど、様々なタイプのニューラルネットを実装可能
- 直観的: ネットワーク構成を直観的に記述できる
個人的には、さらに一つ「インストールが簡単」というのも挙げたいと思います。
ディープラーニング系のフレームワークはどれもインストールが面倒なものが多いのですが、Chainerは依存ライブラリが少なく簡単に導入・・・できたんですが、1.5.0からCythonを使うようになりちょっと手間になりました。インストール方法については以下をご参照ください。
また、Chainerは上記の通り記法が直観的かつシンプルなので、単純なネットワークからより複雑な、いわゆるディープラーニングと呼ばれる領域まで幅広くカバーできます。他のディープラーニング系のライブラリはディープでない場合完全にオーバースペックですし、かといってシンプルなライブラリ(PyBrainなど)ではディープだと厳しい、という状況だったので、この点もメリットとして大きいと思います。
今回はそんな魅力的なChainerの使い方について解説しますが、Chainerを扱うには(割と深い)ニューラルネットワークに関する知識が必要不可欠です。そのため、ニューラルネット側の知識が不十分だとはまることがままあります(私ははまりました)。
よって、ここではまずニューラルネットワークの仕組みについてざっと説明し、後の段でそれをどうChainerで実装するのかついて解説していきたいと思います。
ニューラルネットワークの仕組み
構成
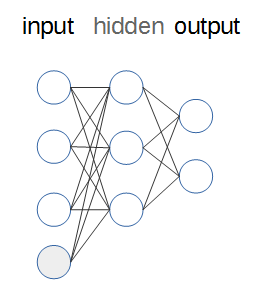
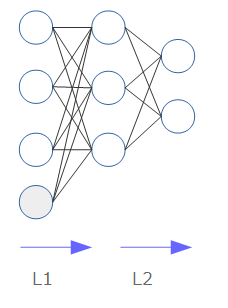
ニューラルネットワークの構成は、以下のようになっています(余談ですが、ノード間の線を引くのが毎回面倒でなりません)。
- ニューラルネットワークは、入力を受け取るinput層、出力を行うoutput層、その間の任意の数の隠れ層(hidden)から構成されます。上図では、隠れ層は1層になります。
- 各層には、任意の数のノードが存在します。このノードは、実体としては入力を受け取り値を出力する単なる関数です(後述します)。
- 入力に際しては、実際の入力とは別に独立した値を入れることがあります。これをバイアス(bias)ノードと呼びます(図中の灰色のノードで、通常値は1です。$ax+b$における$b$(切片)のようなものです)。
伝播
inputからの入力がどのようにoutputまでたどり着くのか、詳しく見ていきます。
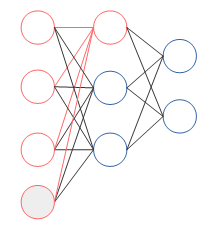
下図は、隠れ層の第一ノードにinputからの入力が行われる様子を見やすくしたものです。
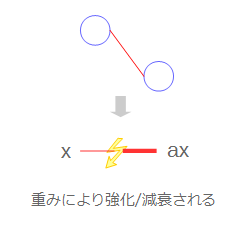
4つのinputが伝わっているのがわかります。inputはそのまま直に伝わるのでなく、重みがかけられます。
ニューラルネットワークは脳の中のニューロンの構成をまねたものですが、これと同様入力(刺激)が伝播する際、弱められたり強められたりするものだと思ってください。数式的に表現すれば、入力が$x$だとしたら、$ax$という感じで$a$という重みが掛けられます。
さて、ここでaxという入力を受け取ったわけですが、ノードは受け取ったこの値をそのまま次の層に横流しするわけではありません。
脳の中ではある閾値を超えた入力でないと次の層には伝播させないという仕組みがあるそうで、ここでもそれを真似て、受け取った入力を次層への出力へ変換します。数式的に表現すれば、入力を次層への出力に変換する関数を$h$とし、その出力値は$h(ax)$で表現できます。この関数$h$を、活性化関数と呼びます。
まとめると、ニューラルネットワークにおける値の伝播にとって重要な要素は、以下二点になります。
- 重み(weight): 入力された値がどれくらい強化/減衰されるかを決定する
- 活性関数(activation function): 受け取った値を、どのように次の層へ渡すか
端的に見れば、ニューラルネットワークは受け取った入力に対して重みをかけて出力しているに過ぎません。そのため、一層のニューラルネットワークは線形回帰やロジスティック回帰とほぼ同義になります。
そう考えると、ノード数、層数の操作がどのような意味を持つのかが明確になってきます。
- ノード数を増やす: 扱う変数を増やし、多数の要素を加味して値/境界を決定できるようにする
- 層数: 直線境界をどんどん組み合わせていき、複雑な境界を表現できるようにする(一層は線形、二層は凸領域、三層は凸領域の中に穴が開いたような領域・・・とどんどん複雑になる。はじめてのパターン認識 第7章 パーセプトロン型学習規則参照)
ニューラルネットワークを扱う場合、適当にノード数や層数をガチャガチャしてしまうこともあるかと思いますが、しっかりデータをプロットし適切なノード数・層数にあたりをつけることも肝要です。
学習
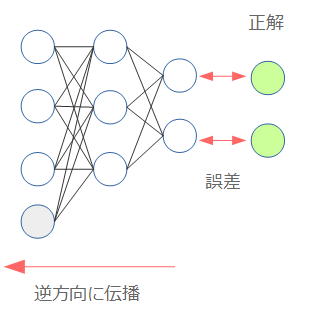
ニューラルネットワークを学習させるためには、誤差逆伝播法(Backpropagation)という手法を用います。
誤差とはニューラルネットワークから出力した値と、実際の値との間の差異になります。Backpropagationは、この誤差をその名の通り後ろ(出力層=output層)から伝播させていき、各層の重みを調整するという手法です。
Backpropagationの詳細は他に様々な説明があるためここでは深入りしませんが、重要な点は以下2点になります。
- 誤差の計算方法: ニューラルネットワークから出力した値と、正解データの間の誤差をどのように計算するか
- コードの中では、cost function、loss function(あるいは単にloss)、error functionなどと定義される
- 重みを調整する方法: 計算された誤差をもって、どのように重みを調整していくのかを決定します
- コードの中ではoptimizerとして定義される
なお、どれくらいの学習データを利用して上記の「誤差を計算し、重みを更新する」という操作を行うかはいくつか手法があります。
- バッチ: 全学習データを用い、誤差の平均から一気に更新する
- オンライン: データ一件ごとに逐次更新する
- ミニバッチ: バッチとオンラインの中間のような手法。全学習データの中から幾つかサンプルを取り用いる(よく使われる手法)。
利用した学習データに対して更新を終えるのが、1エポックというサイクルになります。通常は、このエポックを何回か繰り返して学習していきます。
ただ、単純に繰り返しているとあまりよろしくないので、エポックの度に学習データをシャッフルしたり、ミニバッチの場合はミニバッチの取得位置をずらしたりランダムにサンプリングしたりします。
このエポックは学習の途中経過を確認したり、パラメーターの再調整を行ったりと、ニューラルネットワークの学習において重要な単位になっています。
Chainerによる実装
ニューラルネットワークについて説明した内容を、ここで一旦まとめておきます。
- 構成: 複数のノードを持つ層を重ねることで構築される
- 伝播: 入力に対し重みをかけ、活性化関数を経由することで次層への出力へ変換する
- 学習: 誤差を計算し、それを基に各層の重みを調整する
では、Chainerでの実装と上記のポイントを対応させながら見ていきます。
構成
Chainerでは、ニューラルネットワークはChainで構成します(1.4まではFunctionSet)。
以下は、今まで説明に使っていた4-3-2型のニューラルネットワークを定義したものです。
from chainer import Link, Chain, ChainList
import chainer.functions as F
import chainer.links as L
class MyChain(Chain):
def __init__(self):
super(MyChain, self).__init__(
l1=L.Linear(4, 3),
l2=L.Linear(3, 2)
)
def __call__(self, x):
h = F.sigmoid(self.l1(x))
o = self.l2(h)
return o
※注釈
-
Chainは継承しなくても差し支えないようですが、CPU/GPUのマイグレーションやモデルの保存などはChainを継承しないとできないので、素直に継承した方がいいと思います。なお、単純な全結合であればわざわざクラスを作る必要はなく、Chain(l1=..., l2=...)で良いようです。 - 1.5からパラメーター付の関数(=最適化の対象となる)はLink、純粋な関数(sigmoidなど)はFunctionと役割が明確に分けられました。
あれ、隠れ層は一層じゃなかったっけ?と思った方は最もだと思います。上記のl1、l2については以下の図を参照してください。
このように層と層の間の伝播を考えていくと、2層になるというからくりです。実際、L.Linearは伝播の際の重みを保持しており、入力に対しこの重みをかける操作を担います。
伝播
伝播の処理は、上記の通りChainクラスの__call__に実装を行います。
def __call__(self, x):
h = F.sigmoid(self.l1(x))
o = self.l2(h)
return o
※注釈
- 1.4まで
forwardとして書いていた処理は、__call__に書くことになります(Pythonでは、__call__を定義しておくと、例えばmodelというインスタンスからmodel()とすると__call__に書いた処理が呼べます)。
ここでは入力xに対し重みをかけて(self.l1(x))、次の層へは活性化関数としてよく利用されるシグモイド関数を経由した値を渡しています(h=F.sigmoid(self.l1(x)))。最後の出力では次の層へ渡すための処理は不要なので、活性化関数は使っていません(o = self.l2(h))
学習
学習に際しては、まず予測した値と実際の値との間の誤差を計算する必要があります。これは単純に関数として実装してもよいですが(Chainer内ではlossfunという名前が一般的)、分類問題ならClassifierを使うと楽です。
from chainer.functions.loss.mean_squared_error import mean_squared_error
model = L.Classifier(MyChain(), lossfun=mean_squared_error)
実はClassifierも実体はLink、つまりパラメーターつきの関数で、__call__内でMyChainから出力される値と教師データの誤差を計算しています(計算のためのFunctionは当然指定可能です(上記ではmean_squared_error))。
1.5ではこのLinkをつなげられるようになった点が非常に大きく、モデルの再利用性がぐっと高くなりました。上記でも、本体のモデルとそれを利用して誤差を計算する処理とをきれいに分けて書くことができているのが分かると思います。
誤差を計算した後は、これが最小となるようモデルの最適化を行います(上述のBackpropagation)。この役割を担うのがoptimizerとなり、MNISTのexampleの学習の箇所は、以下のようになっています。
# Setup optimizer
optimizer = optimizers.Adam()
optimizer.setup(model)
...(中略)...
# Learning loop
for epoch in six.moves.range(1, n_epoch + 1):
print('epoch', epoch)
# training
perm = np.random.permutation(N)
sum_accuracy = 0
sum_loss = 0
for i in six.moves.range(0, N, batchsize):
x = chainer.Variable(xp.asarray(x_train[perm[i:i + batchsize]]))
t = chainer.Variable(xp.asarray(y_train[perm[i:i + batchsize]]))
# Pass the loss function (Classifier defines it) and its arguments
optimizer.update(model, x, t)
基本的なステップとしては、以下3つです。
- optimizerを作成(
optimizers.Adam()) - optimizerにモデルをセット(
optimizer.setup(model)) - optimizerでモデルを更新(
optimizer.update(model, x, t))
中核となるのは更新を行っているoptimizer.updateです。1.5からはlossfunを引数に渡すことで自動的に渡されたlossfunによる誤差計算、伝播(backward)を行ってくれるようになりました。もちろん、今まで通りmodel.zerograds()で勾配を初期化してから自前で誤差の計算・伝播を行い(loss.backward)、optimizer.updateを呼ぶことも可能です。
このように、Chainerではモデルを定義したらあとは簡単に最適化ができるよう設計されています(Define-and-Run)。
そして、学習したモデルはSerializerを利用することで簡単に保存/復元が可能です(optimizerについても保存可能です)。
serializers.save_hdf5('my.model', model)
serializers.load_hdf5('my.model', model)
後は、実際実装する上でのTipsを幾つか挙げておきます。
- Chainerはfloat32をメインで扱うため、ちゃんとこの型にしておかないとエラーになります。numpyはデフォルトだと
float64のため注意です。 - loss functionの想定している型をきちんと把握しておく必要があります。例えば、分類問題でよく利用される
softmax_cross_entropy.pyは、教師データが(ラベルを表す)int32型であることを想定しています。ここをfloatで渡すとエラーになるので注意してください。 - 1.5から?、計算処理のフローをグラフ表示できるようになりました(Visualization of Computational Graph)。モデルがきちんと構築できているか、確認するのによいでしょう。
多分最初にはまるのは主に型系のエラーだと思います。Chainerは型に始まり型に終わる・・・かはわかりませんが、「型に始まる」のは間違いないので、この点に気を付けてぜひ利用してみてください。