はじめに
この記事では、機械学習の最も強力な手法の一つであるアンサンブル学習の中でも、特にAdaBoostについて、二つの損失関数を用いた実装も含めてご紹介したいと思います。
実装に際しては以下の記事を参考にさせていただきました。
機械学習におけるアルゴリズムAdaboostを実装をしながら丁寧に理解しようとした(+行列(array)計算も理解が深まった)
アンサンブル学習概略
アンサンブル学習とは、複数の予測器の予測結果を総合する手法のことで、それぞれの予測器一つだけを用いた時よりも精度の高い予測結果を得ることができます。
予測結果を総合するときにはそれぞれの予測器の予測結果の多数決を用いる手法(ハード投票)と、クラスごとに各予測器の予測確率を平均して、その最大値を予測クラスとする手法(ソフト投票)とがあります。
AdaBoostでは各予測器の予測精度に応じた重みを計算し、その重みをベースにしたハード投票を採用しています。
AdaBoost訓練手法と予測手法
AdaBoostはサンプルに与えられた重みを更新し、修正を繰り返しながら複数の予測器を逐次的に学習していく手法です。
具体的にはまず、各サンプルに与えられた重みを用いて予測器を学習し、その予測結果において、間違ったサンプルについては重みを大きくします。それらの更新された重みを用いて次の予測器を学習します。それまでの予測器が間違いがちであったサンプルについては重みが大きくなり、それらのサンプルに対して次の予測器は重点的に学習するため、予測の誤りを修正するように各予測器が学習され、その結果全体の予測精度が向上します。
予測器には決定株(Decision Stump) と呼ばれる深さ1の決定木が用いられることが多いです。
AdaBoostの学習アルゴリズムは以下のようになっています。
まずサンプルの重みを初期化します。
w_i = \frac{1}{N}
Nはサンプル数です。
次に重みを用いて学習した予測器の予測を得ます。
\widehat{y_i} = H_j(x_i)
$H_j$はj番目の予測器、$\widehat{y_i}$は予測ラベルです。
次に予測ラベルと正解ラベルを比較して誤り率を計算します。
r_j = \frac{\sum_{i=1, \widehat{y_i} \neq y_i}^{N} w_i}{\sum_{i=1}^{N} w_i }
次に誤り率から予測器の重みを計算します。
\alpha_j = \log \frac{1-r_j}{r_j}
予測器の重みは誤り率$r_j$が0.5よりも大きければ負に、0.5よりも小さければ正になります。このように、予測精度の低い予測器の重みは小さく、予測精度の高い予測器の重みは大きくなります。
予測器の重みを使ってサンプルの重みを更新します。
w_i = \left\{
\begin{array}{l}
w_i \quad (\widehat{y_i} = y) \\
w_iexp(\alpha_j) \quad (\widehat{y_i} \neq y)
\end{array}
\right.
更新された重みを用いて次の予測器を学習します。
\newcommand{\argmax}{\mathop{\rm argmax}\limits}
- Adaboostの予測
\widehat{y} = \argmax_k \sum_{\substack{j=1 \\ H_j(x)=k}}^{M} \alpha_j
予測時には各予測器の予測クラスを計算し、各クラスごとにそのクラスだと予測した予測器の重み$\alpha_j$ (重要度)を足し合わせ、最大値をとるクラスを予測結果とします。
損失関数
機械学習アルゴリズムの学習(訓練)では損失関数を最小化することを目標とします。
本記事では、決定株を用いたAdaboostの損失関数として、weight損失関数(仮)
とCART損失関数の二つの損失関数を採用しました。weight損失関数とは仮の名前で、記事
機械学習におけるアルゴリズムAdaboostを実装をしながら丁寧に理解しようとした(+行列(array)計算も理解が深まった)で用いられているものです。
Adaboostの予測器として用いられる決定株の学習では、特徴量とその閾値の組みを全て試し、損失関数が最小となる組み合わせを覚えておいて予測時に使用します。
予測サンプルが与えられると、学習時に覚えておいた特徴量が閾値より大きいか小さいかでクラスを予測します。
- weight損失関数
weight損失関数では、ある特徴量について閾値より大きいものをクラス1小さいものをクラス2というふうに決め打ち、その仮の予測が間違っていたものの重みを足し合わせて損失関数とします。
weightcost = \sum_{\substack{i=1 \\ \widehat{y_i} \neq y_i}}^{N} w_i
- CART損失関数
CART(Classification And Regression Tree)損失関数は決定木の学習で使われる損失関数です。今回は予測器に深さ1の決定木である決定株を用いるため、この損失関数を使うことができます。ある特徴量と
その閾値について、閾値よりも大きい方を右側、小さい方を左側と呼ぶことにすると(特徴量でソートしたと考えるとわかりやすいです)、それぞれの領域
がどれほど不純か(色々なクラスが混在している状態)を示す不純度$G_{right}, G_{left}$と、それぞれの領域のサンプル数の割合$\frac{N_{right}}{N}, \frac{N_{left}}{N}$ をかけて足し合わせたものを損失関数とします。
不純度の指標としては、ジニ係数やエントロピーがありますが、今回はジニ係数を用います。
G = 1 - \sum_{k=1}^{K} p_k^2
$p_k^2$はその領域に属するサンプルの中で正解ラベルがkのものの割合です。
CARTcost = \frac{N_{left}}{N} G_{left} + \frac{N_{right}}{N} G_{right}
上記ではサンプルの個数ベースで式が書かれていますが、AdaBoostの予測器として用いる決定株を学習する時は各サンプルの重みを用いて計算する必要があります。
実装
以下が決定株の実装です
class Decision_Stump:
def __init__(self,axis=None, threshold=None, sign=1, cost_name='weight_cost'):
self.axis = axis
self.thresh = threshold
self.sign = sign
self.cost_name = cost_name #weight_cost, cart_cost
def get_c(self, ba_ary, sorted_sample_weight):
cost, sign = float('inf'), 1
if (ba_ary==0).sum() == len(ba_ary):
return cost, sign
#calc m
m_all = sorted_sample_weight.sum()
m = (ba_ary!=0) @ sorted_sample_weight
#calc gini
p1 = ( (ba_ary==1) @ sorted_sample_weight ) / m
p2 = ( (ba_ary==-1) @ sorted_sample_weight ) / m
gini = 1.0 - p1**2 - p2**2
cost = m/m_all * gini
if (ba_ary==1).sum() < (ba_ary==-1).sum():
sign = -1
return cost, sign
def fit_one_axis(self, x, y, sample_weight, margin=0.1):
sorted_ind = np.argsort(x)
sorted_x = x[sorted_ind]
sorted_y = y[sorted_ind]
sorted_sample_weight = sample_weight[sorted_ind]
N = len(x)
threshs = []
signs = []
costs = np.full((2, N), float('inf'))
for i in range(N):
thresh = x.min() - margin*(x.max()-x.min())
if i!=0:
thresh = (sorted_x[i-1] + sorted_x[i]) / 2.0
threshs.append(thresh)
if self.cost_name == 'weight_cost':
mistakes = np.zeros((2, N))
pred_1 = np.ones(N)
pred_1[:i] = -1
pred_2 = - pred_1
mistakes[0] = (pred_1 != sorted_y)
mistakes[1] = (pred_2 != sorted_y)
cost = mistakes @ sorted_sample_weight
costs[:,i] = cost
min_arg = np.argmin(cost)
if min_arg == 0:
sign = 1
else:
sign = -1
elif self.cost_name == 'cart_cost':
before_i, after_i = sorted_y[:i], sorted_y[i:]
before_i = np.concatenate([before_i, np.zeros(N-len(before_i))])
after_i = np.concatenate([np.zeros(N-len(after_i)), after_i])
cs = {'c_left': -1, 'c_right': -1}
cs['c_left'], _ = self.get_c(before_i, sorted_sample_weight)
cs['c_right'], sign = self.get_c(after_i, sorted_sample_weight)
c_cart = cs['c_left'] + cs['c_right']
if sign == 1:
costs[0, i] = c_cart
elif sign == -1:
costs[1, i] = c_cart
else:
print('number of sign is wrong')
else:
print('Not Defined Cost Name')
signs.append(sign)
min_cost_ind = np.unravel_index(np.argmin(costs, axis=None), costs.shape)
return threshs[min_cost_ind[1]], costs[min_cost_ind], signs[min_cost_ind[1]]
def fit(self, X, y, sample_weight):
axes, threshs, costs, signs = [], [], [], []
for axis in range(X.shape[1]):
thresh, cost, sign = self.fit_one_axis(X[:, axis], y, sample_weight)
axes.append(axis)
threshs.append(thresh)
costs.append(cost)
signs.append(sign)
# axes, threshs, costs, signs = np.array(axes), np.array(threshs), np.array(costs), np.array(signs)
ind = np.argmin(costs)
self.axis = axes[ind]
self.thresh = threshs[ind]
self.sign = signs[ind]
def predict(self, X):
return self.sign * (2 * (X[:, self.axis]>=self.thresh) -1 )
Adaboost本体の実装です
class AdaBoost:
def __init__(self, model, n_estimators=100, cost_name='weight_cost'):
self.model = model # Decision_Stump
self.n_estimators = n_estimators
self.clfs = [self.model(cost_name=cost_name) for _ in range(self.n_estimators)]
self.alpha = np.zeros(self.n_estimators)
def fit(self, X, y):
sample_weight = np.ones(len(X)) / len(X)
for i in range(self.n_estimators):
clf = self.clfs[i]
clf.fit(X, y, sample_weight)
mistakes = (clf.predict(X) != y )
err_rate = (mistakes @ sample_weight) / sample_weight.sum()
alph = np.log(( 1.0- err_rate) / err_rate)
self.alpha[i] = alph
sample_weight = sample_weight * np.exp(mistakes*alph)
sample_weight = sample_weight / sample_weight.sum()
def predict(self, X):
temp_pred = np.zeros((len(X), self.n_estimators))
for i in range(self.n_estimators):
temp_pred[:, i] = self.clfs[i].predict(X)
cls1 = (temp_pred==1) @ self.alpha
cls2 = (temp_pred==-1) @ self.alpha
return 2 * (cls1>=cls2) - 1
トイデータセットを用いた結果比較
二つのトイデータセットを用いて、weight損失関数とCART損失関数を比較してみました。
- moonsデータセット
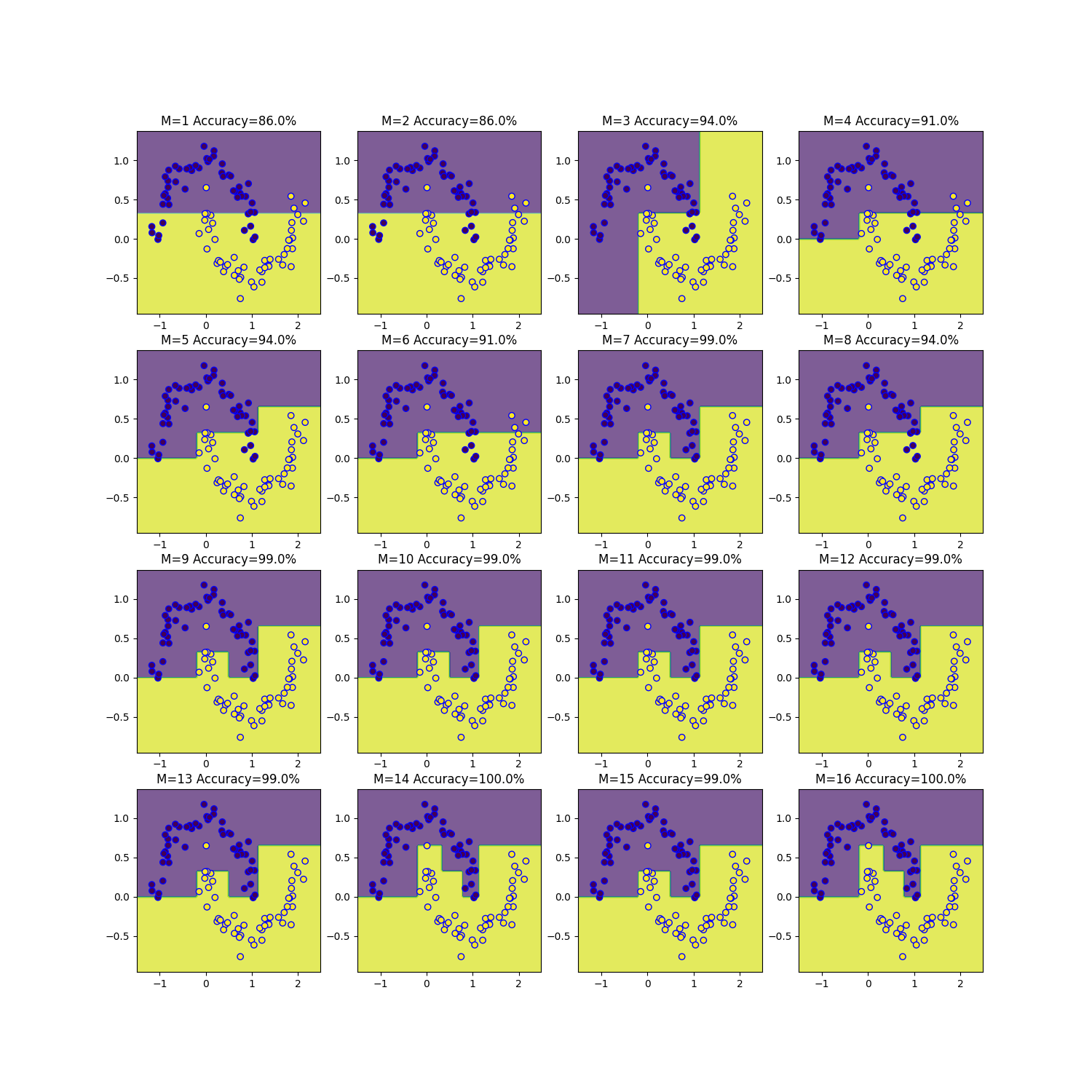
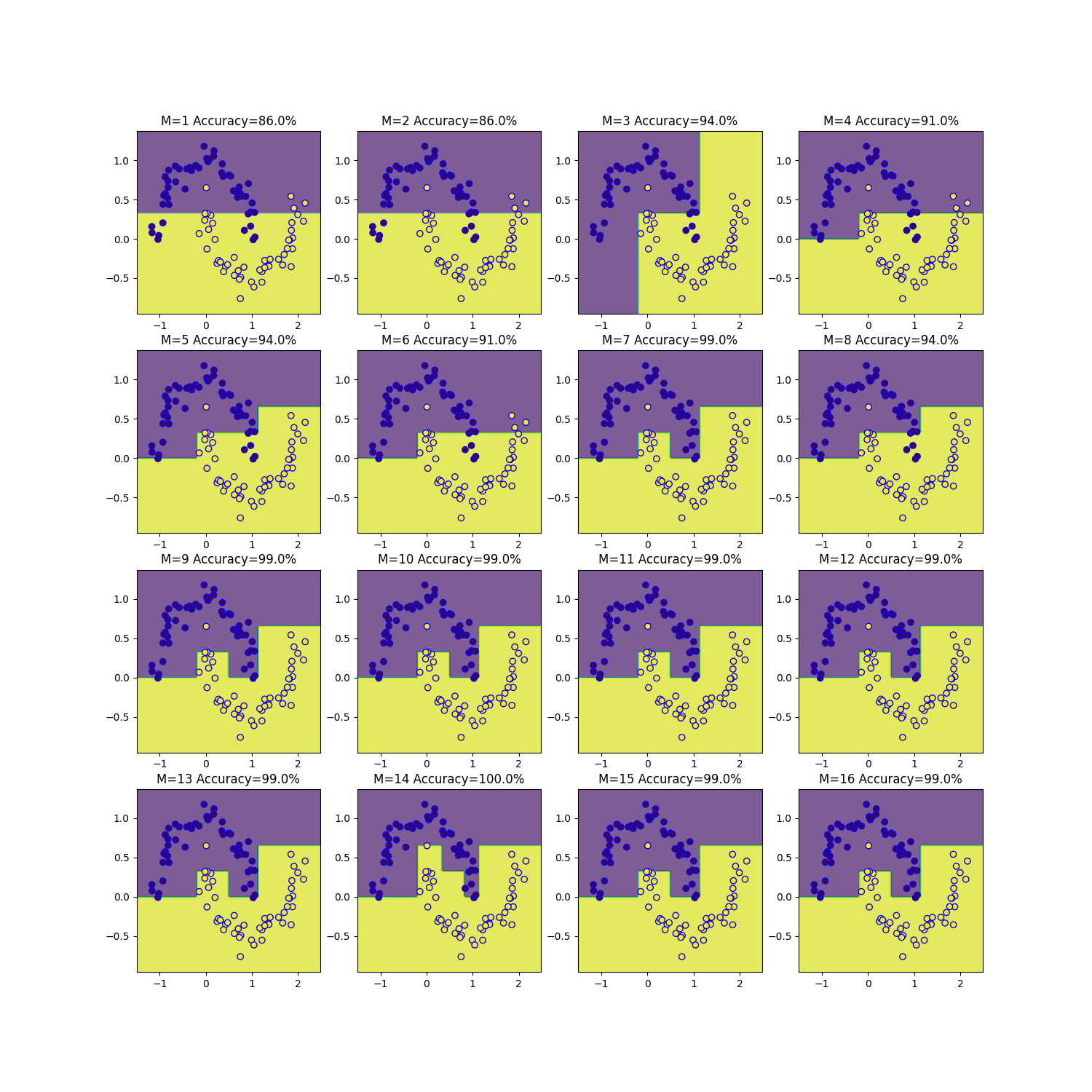
AdaBoostの予測器の数を1~16まで変えて決定境界を可視化しました。
以下はコードです
X, y = datasets.make_moons(n_samples=100, noise=0.1, random_state=1)
y = 2*y-1
model = AdaBoost(Decision_Stump, n_estimators=1, cost_name='cart_cost')
model.fit(X, y)
y_pred = model.predict(X)
moonsデータセットを取得しラベルを1, -1に変更しています。
モデルを作成して学習、予測を行います。
def get_min_max(x, margin=0.1):
x_width = x.max() - x.min()
x_min = x.min() - margin*x_width
x_max = x.max() + margin*x_width
return x_min, x_max
get_min_maxは特徴量の最小値と最大値を少しマージンを取って返す関数です。
margin = 0.1
nx1, nx2 = 100, 100
num_clf = np.arange(16) + 1
cost_name = 'cart_cost' # cart_cost, weight_cost
x1_min, x1_max = get_min_max(X[:, 0], margin)
x2_min, x2_max = get_min_max(X[:, 1], margin)
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max, nx1), np.linspace(x2_min, x2_max, nx2))
fig, axs = plt.subplots(4, 4, figsize=(15, 15))
for i in range(len(num_clf)):
model = AdaBoost(Decision_Stump, num_clf[i], cost_name)
model.fit(X, y)
y_pred = model.predict(X)
acc_rate = (y_pred==y).sum() / len(X)
print('model', i+1,'の正答確率は', acc_rate*100, '%です')
zz = model.predict(np.c_[xx1.ravel(), xx2.ravel()]).reshape(xx1.shape)
ind = np.unravel_index(i, shape=np.shape(axs) )
ax = axs[ind[0]][ind[1]]
ax.contourf(xx1, xx2, zz, alpha=0.7)
ax.scatter(X[:, 0], X[:,1], c=y, edgecolor='b')
ax.set_title(f'M={num_clf[i]} Accuracy={acc_rate*100}%')
どちらの損失関数を用いても、ほとんど同じ結果となりました。M=16のときにweight損失関数では正解確率100%であるのに対しCART損失関数では99%となったのが違いです。
M=100までやってもM=16とM=22の時のみ違いが生じました。
- breast cancerデータセット
サンプル数569 特徴量数30のデータセット
moonsデータセットのように特徴量数が2ではないのでAdaBoostの決定境界を描画することはできないのですが、二つの損失関数の比較のために予測器の数を1~16まで変えた時の正解確率を表示してみました。
こちらも二つの損失関数でデータへのフィッティングという意味ではほとんど違いが見られませんでした。
data = datasets.load_breast_cancer()
X = data.data
y = data.target
y = 2*y-1
num_clf = np.arange(16)+1
cost_name = 'weight_cost'
for i in range(len(num_clf)):
model = AdaBoost(Decision_Stump, num_clf[i], cost_name)
model.fit(X, y)
y_pred = model.predict(X)
acc_rate = (y_pred==y).sum() / len(X)
print('model {} の正答確率は {:4g} %です'.format(i+1, acc_rate*100))