はじめに
Kaggleなどでよく使われているXGBoostなどの元となるブースティングについてまとめます。ブースティングのアルゴリズムの中でもAdaboostについて実装をしながら理解していきたいと思います。
@amber_kshz さんのこちらの記事を使用させて頂き、実装をしました。
PRML14章のBaggingとAdaBoostをPythonで実装
https://qiita.com/amber_kshz/items/8869d8ef7f9743b16d8d
**特に、行列(array)を用いて効率よく早く計算する手法を学ぶことができました。**その方法についてもまとめていければと思います。
要点は下記です。
- ブースティング(Boosting)を理解する
- Adaboostのアルゴリズムを理解する
- Adaboostを実装することで理解を深める
- 決定株(Decision Stump)を理解する
- 実際に動かしてみる+試行回数による差を評価する
ブースティング(Boosting)を理解する
弱学習器と呼ばれる学習器を組み合わせる手法をアンサンブル学習と呼びます。代表的なアンサンブル学習は大きく4つに分けることができます。
- バギング(訓練データから複数の弱学習器で判別し、平均化(サンプリング重複あり))
- ペースティング(訓練データから複数の弱学習器で判別し、平均化(サンプリング重複なし))
- スタッキング(弱学習器の重要度を考慮して荷重平均)
- (今回)ブースティング(弱学習器の精度を向上させて強学習器を作る)
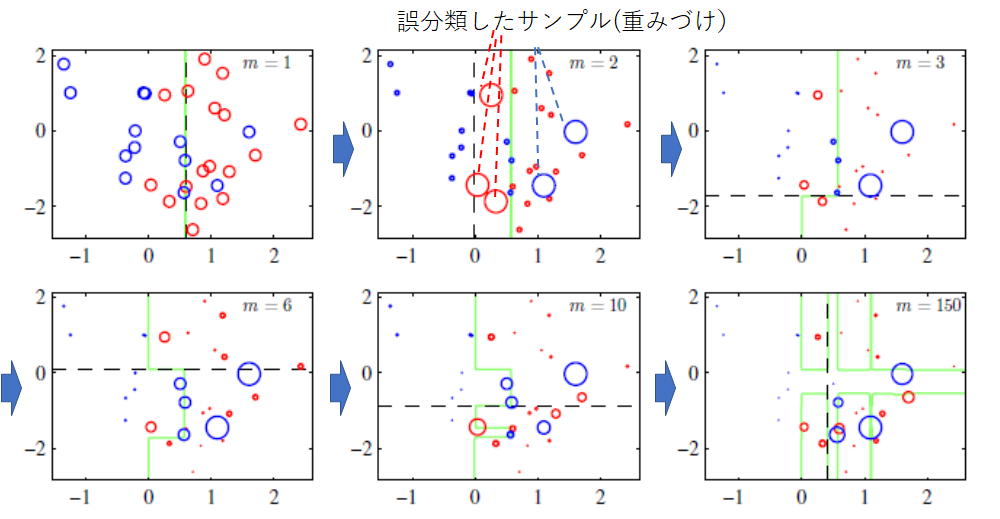
そのアンサンブル学習の中でも、弱学習器を連続的に学習させて、精度が向上するように修正させるアルゴリズムをブースティングと呼びます。間違えた(=誤分類)サンプルに対して、注意を払って次の学習を行うことでより精度の高い学習器にさせることを狙います。
下記図にその一連の流れを示します。$m$が試行回数で左上から右下に向かって試行回数が増えていきます。青と赤丸を分類していきたいのですが、誤分類したサンプルは大きく丸付けしています。その誤分類したサンプルをどうにか分けようと緑の分類線が動いてくことがみてわかります。
似た学習器に、**バギング(Bagging)**があります。バギングの場合、独立して学習した結果を平均化します。このそれぞれの学習器は独立である一方で、ブースティングの場合は前に学習した結果を後の学習でも用いる点が異なります。
Adaboostのアルゴリズムを理解する
さて、次にAdaboostのアルゴリズムについて理解します。Adaboostは、Adaptive Boosting:適応的ブースティングの略称になります。1997年に発表されたアルゴリズムです。
前の予測器で誤った判断をした部分に余分に注意を払うような修正を、新しい予測器で行う考え方を適用させているのがAdaboostです。
A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting
https://www.sciencedirect.com/science/article/pii/S002200009791504X
具体的なアルゴリズムは下記になります。
前提
- $N \in \mathbb{N}$ : サンプルデータの個数
- $X = (x_0, x_1, \dots, x_{N-1})$ : サンプルデータ点。$x_n \in \mathbb{R}^D$とします。
アルゴリズム
- 入力 : 訓練データは$(X, T)$、ベース分類器を$y$、分類器の個数は$M$とします。
- 訓練データの重み$(w_0, w_1, \dots, w_{N-1})$を$w^{(0)}_{n} = 1/N$と初期化します。
- $m=0,1,....M-1$について以下を繰り返します。
(a)分類器$y_m(x)$を下記で表す誤差関数$J_m$を最小化するようにテストデータに合わせる
$$
\begin{align}
J_m = \sum_{n=0}^{N-1} w^{(m)}_{n} I \left[ y(x_n, \theta_m) \neq t_n \right]
\end{align}
$$
⇒このとき、$I \left[ y(x_n, \theta_m) \neq t_n \right]$はテストデータと予測値が一致していれば0(=正解)、間違っていると1になります。従って、正解数が多いと$J_m$が小さくなります(=誤差関数の役割を果たしておりOK)。
(b) ベース分類器の誤差から$\epsilon_m、\alpha_m$を計算します。$\epsilon_m$は誤答率を表し、$\alpha_m$は重みパラメータへ反映させる係数になります。
$$
\begin{align}
\varepsilon_m &:= \frac{\sum_{n=0}^{N-1} w^{(m)}_{n} I \left[ y(x_n, \theta_m) \neq t_n \right]}{\sum_{n=0}^{N-1} w^{(m)}_{n}} \
\alpha_m &:= \log \left(\frac{1 - \varepsilon_m}{\varepsilon_m} \right)
\end{align}
$$
(c)前のステップで求めた$\alpha_m$を用いて、重み$w$を
$$
\begin{align}
\tilde{w}^{(m+1)}_{n} &= w^{(m)}_{n} \exp\left\{ \alpha_m I \left[ y(x_n, \theta_m) \neq t_n \right] \right\} \
\end{align}
$$
のように更新します。
⇒このとき予測値とテストデータがあっていると$I$は$0$を示します。逆に間違っていると$1$となるため、重みづけが先ほどの$\alpha$と合わせて更新されます。
Adaboostを実装することで理解を深める
それでは実際に実装に移っていきたいと思います。
決定株(Decision Stump)を理解する
今回、弱学習器は決定株を用います。決定株とは、**あるデータの入力変数どれか一つを選び、その値によって閾値を設定し分類をするというものです。**要は、深さ1の決定木であると理解しています。
さて、下記のプログラムでその決定株クラスを定義しています。
def fit_onedim(self, X, y, sample_weight, axis):
N = len(X)
# Here we sort everything according the axis-th coordinate of X
sort_ind = np.argsort(X[:, axis])
sorted_label = y[sort_ind]
sorted_input = X[sort_ind]
sorted_sample_weight = sample_weight[sort_ind]
pred = -2*np.tri(N-1, N, k=0, dtype='int') + 1
mistakes = (pred != sorted_label ).astype('int')
# The (weighted) error is calculated for each classifier
errs = np.zeros((2, N-1))
errs[0] = mistakes @ sorted_sample_weight
errs[1] = (1 - mistakes) @ sorted_sample_weight
# Here, we select the best threshold and sign
ind = np.unravel_index(np.argmin(errs, axis=None), errs.shape)
sign = -2*ind[0] + 1
threshold = ( sorted_input[ind[1], axis] + sorted_input[ind[1] + 1, axis] ) / 2
err = errs[ind]
return sign, threshold, err
計算を詳しく知る
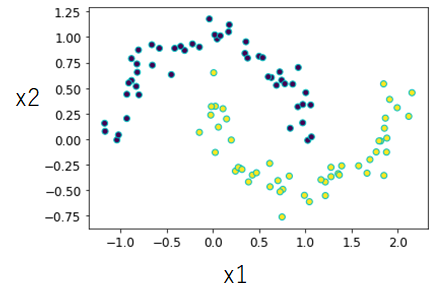
今回は、下記でも示しますがmakemoonsデータセットを用いています。下記画像のようなサンプルデータ数$100$個で、$1$ラベルのデータが$50$個、$-1$ラベルのデータが$50$個ある場合を考えます。
このデータセットは$X=(x_1,x_2)$に格納されています。簡便のため下記np.argsortにより昇順に並べる前のインデックスを定義します。
次に、仮の予測値を与える行列predとしてnp.triメソッド(上下三角行列生成)を行います。

そして、このpred-yをmistake行列として定義します。これにより、99組の正誤表ができました。

この損失関数の最小値をとるときの境界となる$x_1^m,x_1^{m+1}$の平均値が境界線になります。
Adaboostの場合は、さらにここで不正解したラベルについての重みを更新する処理が入ります。
(補足)一致しているかを判別する
このプログラムの中で、良い方法だなと思った点が下記です。予測した値が正解かどうかを真偽値(bool型)で判別しています。先ほどの誤差関数の内容では、当たっていれば$0$、外れていれば$1$でしたので、そのように細工します。
a = np.array([[1,1,1,1],[1,1,1,1],[1,1,0,1]])
b = np.array([1,1,1,0])
c1 = (a != b )
c2 = (a != b ).astype('int')
print(c1)
print(c2)
[[False False False True]
[False False False True]
[False False True True]]
[[0 0 0 1]
[0 0 0 1]
[0 0 1 1]]
こちらに簡単な例を示しています。$a$を予測値、$b$を判別する正解ラベルとします。当たっていることが今回はFalseで$0$を、外れていることが今回がTrueで$1$を返すようなプログラムになっていることが分かります。
実際に動かしてみる+試行回数による差を評価する
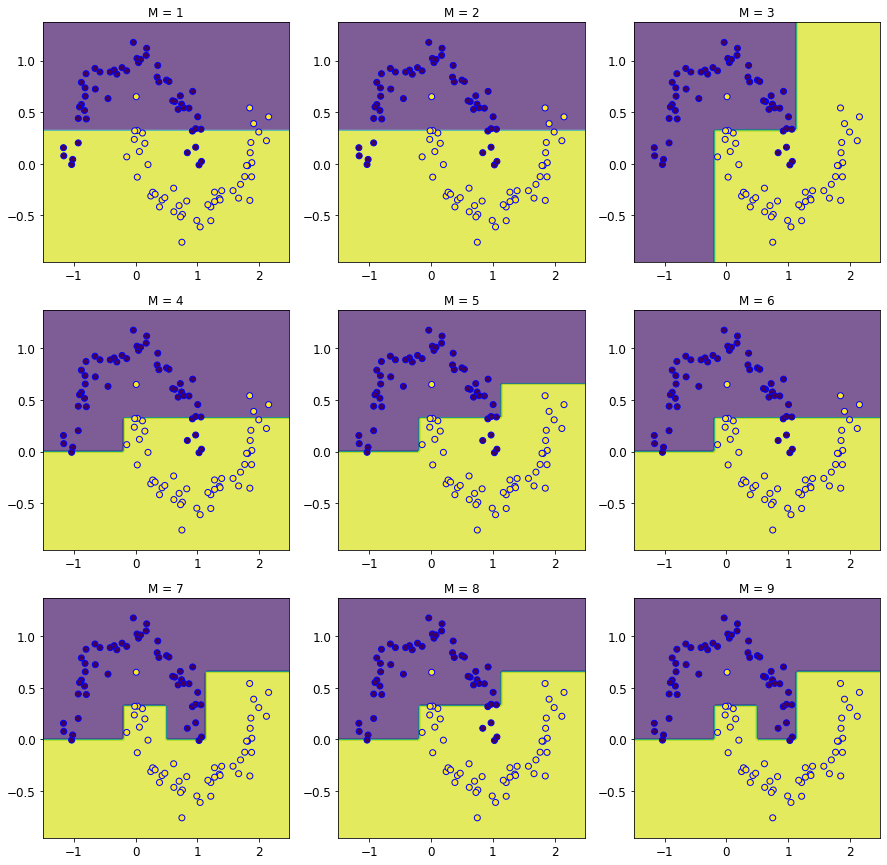
それでは実際に動かしてみましょう。試行回数として、$1~9$まで行ってみます。
num_clf_list = [1, 2, 3, 4, 5, 6,7,8,9]
clfs = [AdaBoost(DecisionStump, num_clfs=M) for M in num_clf_list]
fig, axes = plt.subplots(3, 3, figsize=(15,15))
for i in range(len(clfs)):
clfs[i].fit(X, y)
plot_result(ax=np.ravel(axes)[i], clf=clfs[i], xx=xx, yy=yy, X=X, y=y)
np.ravel(axes)[i].set_title(f'M = {num_clf_list[i]}')
徐々に分類する線が分かれていき、精度のある分類器になっていきそうなことが分かります。決定株の場合、定義からも分かりますが直線で分類しようとするため、非線形な曲線で分類したい場合は難しいことが分かります。
終わりに
今回、Adaboostについて実装を交えて理解を深めました。アルゴリズム自体は分かりやすいものの、いざ実装するとなるとnumpyを初めとする行列の計算をよく理解しておかないと進められないことが分かりました。
ここからXGboostなどKaggleでよく用いられているアルゴリズムを理解していくことで、解析力をつけてければと思います。
プログラム全文はこちらです。
https://github.com/Fumio-eisan/adaboost_20200427