AtCoder Beginners Contest 327 (ABC327) をPythonで解きました。
見やすいコードを書く練習も兼ねてます。
A - ab
問題
文字列 $S$ の中に、a と b が隣り合ったところはありますか?
考察
「a と b が隣り合っている」というのは、「文字列 $S$ の中に ab もしくは ba がある」というのと同じです。
「ab が文字列 $S$ の中にある」というのは、'ab' in S で表せます。
これをつかって、「ab が文字列 $S$ の中にある」と「ba が文字列 $S$ の中にある」の2つのうち1つ以上が成り立つときにYesを出力し、それ以外のときはNoを出力すれば正解です。
コード
N = int(input())
S = input()
if ('ab' in S) or ('ba' in S):
print("Yes")
else:
print("No")
B - A^A
問題
$B$ が与えられます。 $A^A=B$ となる $A$ は存在しますか?
考察
制約より、 $B\leqq10^{18}$ です。
$A=18$ のときは $A^A=18^{18} < 10^{18}$ となるので、大雑把に $A=18$ くらいまで調べれば十分なのが分かります。なので、うまく工夫しなくても $A=1,2,3,\cdots ,18$ と1つ1つ調べていけばokです。
不安だったら、$A=100$ くらいまで調べちゃっても大丈夫です。
コード
B = int(input())
for A in range(1, 19):
if A ** A == B:
print(A)
exit()
print(-1)
C - Number Place
問題
与えられた$9\times 9$マスは、数独(ナンプレ)の条件を満たしていますか?
考察
次の $3$ つの条件を満たしていればokです。
(↓ 問題文より引用)
- $A$ の各行について、その行に含まれる $9$ マスには $1$ 以上 $9$ 以下の整数がちょうど $1$ 個ずつ書き込まれている。
- $A$ の各列について、その列に含まれる $9$ マスには $1$ 以上 $9$ 以下の整数がちょうど $1$ 個ずつ書き込まれている。
- $A$ の行を上から $3$ 行ずつ $3$ つに分け、同様に列も左から $3$ 列ずつ $3$ つに分ける。 これによって $A$ を $9$ つの $3×3$ のマス目に分けたとき、それぞれの $3×3$ のマス目には $1$ 以上 $9$ 以下の整数がちょうど $1$ 個ずつ書き込まれている。
要するに、数独(ナンプレ)の条件と同じです。
一気に条件を $3$ つとも満たしているか調べるのはしんどいので、 $1$ つずつ満たしているかをチェックしていくのがオススメです(下のコードではそれぞれ関数でチェックしています)。
コード
# 各行に1~9が入っているかチェックする
def row_check():
for i in range(9):
se = set()
for j in range(9):
se.add(A[i][j])
if len(se) != 9:
return False
return True
# 各列に1~9が入っているかチェックする
def col_check():
for j in range(9):
se = set()
for i in range(9):
se.add(A[i][j])
if len(se) != 9:
return False
return True
# 各3×3のマスに1~9が入っているかチェックする
def square_check():
# 3×3マスの左上のマスが(si, sj)
for si in [0, 3, 6]:
for sj in [0, 3, 6]:
se = set()
for di in range(3):
for dj in range(3):
i, j = si + di, sj + dj
se.add(A[i][j])
if len(se) != 9:
return False
return True
A = [list(map(int, input().split())) for _ in range(9)]
if row_check() and col_check() and square_check():
print("Yes")
else:
print("No")
D - Good Tuple Problem
問題
$2$ つの数列 $A=(A_1, A_2, \cdots , A_M), B=(B_1, B_2, \cdots , B_M)$ が与えられます。
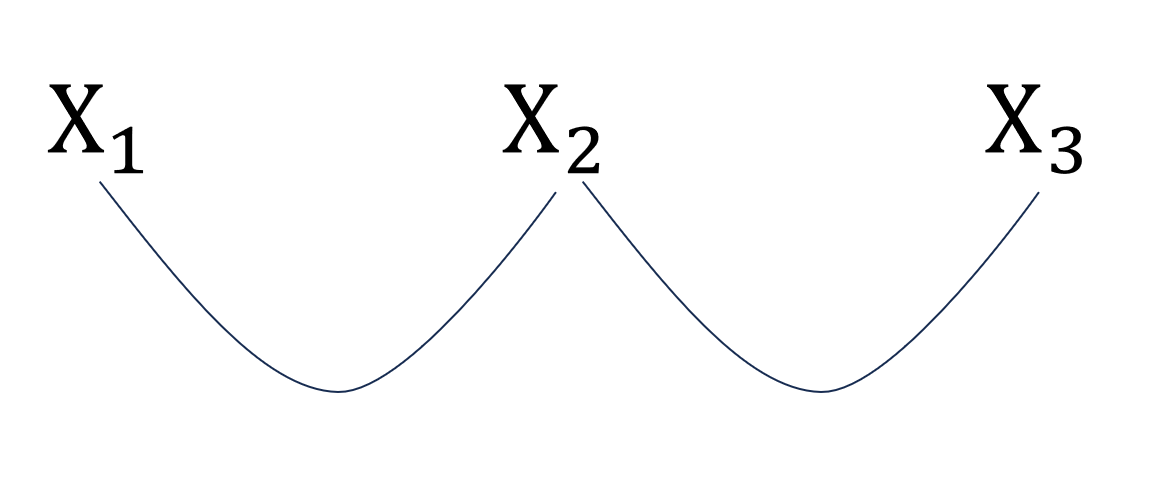
$i=1,2,\cdots ,M$ について $X_{A_i} \neq X_{B_i}$ となるような数列 $X=(X_1, X_2, \cdots, X_N)$ (ただし $j=1,2,\cdots N$ について $X_j=0$ または $X_j=1$ )をつくれますか?
考察
たとえば、サンプル $1$ の $A=(1,2), B=(2,3)$ を考えます。
このときは、 $X_1 \neq X_2$ かつ、 $X_2 \neq X_3$ になればokです。今回は、 $X=(0,1,0)$ や、 $X=(1,0,1)$ が条件を満たします。
このように、 $0$ と $1$ だけで構成して、条件として「こことここは一緒の数にしないでね」と言われる問題は、「二部グラフ判定」とよばれる頻出問題です。
二部グラフ判定の問題は、こんな問題です。
$N$ 個の頂点と $M$ 本の辺からなる単純な無向グラフ $G$ が与えられます。
$i=1,2,\cdots M$ について、 $i$ 番目の辺は頂点$u_i$ と頂点 $v_i$ を結びます。
あなたは各頂点を黒または白のどちらかの色で塗らなければなりません。同じ色に塗られた頂点どうしを結ぶ辺がないように塗ることはできますか?
今回はこの「二部グラフ判定」の問題に置き換えます。
「 $X_{A_i} \neq X_{B_i}$ 」 の条件を、「頂点 $A_i$ と頂点 $B_i$ の間に辺をはり、この $2$ 頂点の色を異なる色にしたい」と言い換えて、無向グラフ $G$ をつくります。
二部グラフ判定の解き方を説明します。
頂点$1,2,\cdots N$ と順番に見ていきます。
もしも、今見ている頂点にまだ色が塗られていなければ、色 $0$ を塗ります。
そして、この頂点と辺で結ばれた頂点すべてについて、今度は色 $1$ を塗ります。
次は、さっき色 $1$ を塗った頂点すべてについて、そこから辺で結ばれた頂点に色 $0$ を塗ります。(すでに色 $0$ が塗られていたらスルーします)
これを繰り返していきます。
色を塗っていく過程で、「色 $1$ を塗ろうとした頂点がすでに色 $0$ で塗られていた」みたいなことが起きていたら、それは二部グラフではありません。
逆に、これが起こらないで最後まですべての頂点を塗り切れたら、そのグラフは二部グラフです。
コード
from collections import deque
N, M = map(int, input().split())
A = list(map(lambda x: int(x) - 1, input().split()))
B = list(map(lambda x: int(x) - 1, input().split()))
G = [[] for _ in range(N)]
for a, b in zip(A, B):
G[a].append(b)
G[b].append(a)
color = [None] * N
for i in range(N):
if color[i] is not None:
continue
color[i] = 1
que = deque()
que.append(i)
while que:
v = que.popleft()
for nv in G[v]:
if color[nv] is None:
color[nv] = 1 - color[v]
que.append(nv)
elif color[nv] == color[v]:
print("No")
exit()
print("Yes")
おまけ
二部グラフ判定のライブラリ化
これまで何度か二部グラフ判定の問題は出題されています。
手元でライブラリ化したものを持っておくと、いつかまた二部グラフ判定の問題が出たときにはやく解けます。
from collections import deque
class BipartiteGraph:
""" 2部グラフ判定クラス
2部グラフかどうかを判定するクラスです。
・つかい方
graph = BipartiteGraph(N): インスタンス生成
graph.add_edge(u, v): 2頂点u, v間に無向辺をはる
graph.draw(): 2部グラフならTrue, そうでないならFalseを返す
graph.color[v]: (draw()をして二部グラフだったときのみ)、頂点vの色(0 or 1) を返す
"""
def __init__(self, n: int) -> None:
self.n = n
self.graph = [[] for _ in range(n)]
self.color = [None] * n
def add_edge(self, u: int, v: int) -> None:
self.graph[u].append(v)
self.graph[v].append(u)
return None
def draw(self) -> bool:
for v in range(self.n):
if self.color[v] is not None:
continue
self.color[v] = 0
que = deque()
que.append(v)
while que:
ov = que.popleft()
for nv in self.graph[ov]:
if self.color[nv] is None:
self.color[nv] = self.color[ov] ^ 1
que.append(nv)
elif self.color[nv] == self.color[ov]:
return False
return True
N, M = map(int, input().split())
A = list(map(lambda x: int(x) - 1, input().split()))
B = list(map(lambda x: int(x) - 1, input().split()))
graph = BipartiteGraph(N)
for a, b in zip(A, B):
graph.add_edge(a, b)
is_bipartite = graph.draw()
if is_bipartite:
print("Yes")
else:
print("No")
E - Maximize Rating
問題
もしも、パフォの悪い回がなかったら...!!
考察1 (具体的に計算してみる)
参加したコンテストのパフォーマンスが、参加した順にそれぞれ $(Q_1, Q_2, \cdots Q_k)$ のとき、レーティング $R$ は次のように計算できます。
$$R=\displaystyle \frac{\sum _{i=1}^{k} (0.9)^{k-i} Q_i}{\sum _{i=1}^{k} (0.9)^{k-i}} - \displaystyle \frac {1200}{\sqrt {k}}$$
...と言われてもパッと見で分かるわけないので、具体的に計算してみます。
サンプル $1$ は、 $P=(1000,600,1200)$ です。
$2$ 回目のパフォーマンスが $600$ のところをなかったことにして、 $Q=(1000, 1200)$ とすると、
$$R=\displaystyle \frac{0.9 \times 1000 + 1.0 \times 1200}{0.9+1.0} - \displaystyle \frac{1200}{\sqrt{2}} = 256.73502...$$
と計算できます。
たとえば、どの回も無かったことにしないで、 $Q=(1000,600,1200)$ だったら、
$$R=\displaystyle \frac{(0.9)^2 \times 1000 + 0.9 \times 600 + 1.0 \times 1200}{(0.9)^2+0.9+1.0} - \displaystyle \frac{1200}{\sqrt{3}} = 248.13908...$$
となります。
なんとなく雰囲気がつかめましたか?
今回は $N=3$ でそんなに数がないからいいですが、テストケースでは最大で $N=5000$ の入力が与えられるので、うまく工夫して計算しましょうという問題です。
考察2 (工夫できるポイントを探す)
計算の回数を減らせるポイントを探していきます。
考察1での計算を見てみると、工夫できそうなポイントは大きく $3$ つあります。
- $(0.9)^x$ の形が何度も出てくるので、事前に $x=0,1,2,\cdots ,N$ について $(0.9)^x$ の計算をする。
- 第 $1$ 項の分母も同じ形が何度も出てくるので、事前に累積和を取っておく。
- 第 $2$ 項も、事前に $k=1,2,\cdots ,N$ について、 $\frac{1200}{\sqrt{k}}$ の計算をしておく。
毎回いちいち計算しないで済むところは、事前に計算しておきましょう。
考察3 (動的計画法DP)
(再掲)
$$R=\displaystyle \frac{(0.9)^2 \times 1000 + 0.9 \times 600 + 1.0 \times 1200}{(0.9)^2+0.9+1.0} - \displaystyle \frac{1200}{\sqrt{3}} = 248.13908...$$
こんな感じで計算するわけですが、第 $1$ 項の分母と第 $2$ 項は事前に計算できています。残りは第 $1$ 項の分子です。
ここからは、第 $1$ 項の分子だけに注目していきます。
パフォ $1000(=P_{1})$ は$(0.9)^2$ をかけるかもしれないし、かける数は $0.9$ かもしれないし、$1.0$ かもしれません。
パフォ $1200(=P_{3})$ は、他にどの回をどう選んだとしても、かける数は $1.0$ です。
ここでDPあるあるの1つ、「DPは自明な方からやる」をつかいます。
$P_1$ から順番に見ていくのではなく、 $P_N$ から逆順に見ていきます。
リスト $dp$ をこう決めます。
$dp[i][j]: (後ろから順に)P[i]まで見て、参加した回数jのときの第1項分子の最大値$
遷移は、もらうDPっぽく次の式で表せます。
$dp[i][j]=\max(dp[i+1][j], dp[i+1][j-1]+(0.9)^{j-1}\times P[i])$
あとは実装するのみです。
コード
import math
INF = float("Inf")
N = int(input())
P = list(map(int, input().split()))
# rui[i]: (0.9)^i
rui = [1]
for _ in range(N):
rui.append(rui[-1] * 0.9)
# bunbo[j]: 参加回数jのときの、第1項分母
bunbo = [0]
for i in range(N):
bunbo.append(bunbo[-1] + rui[i])
# penalty[j]: 参加回数jのときの、第2項
penalty = [INF]
for i in range(N):
penalty.append(1200 / math.sqrt(i + 1))
# dp[i][j]: (後ろから順に)P[i]まで見て、参加した回数jのときの第1項分子の最大値
dp = [[-INF] * (N + 1) for _ in range(N + 1)]
for i in range(N + 1):
dp[i][0] = 0
for i in range(N - 1, -1, -1):
for j in range(1, N - i + 1):
# 参加しないパターン。そのままコピーしてくる
dp[i][j] = dp[i + 1][j]
# 参加するパターン
v = dp[i + 1][j - 1] + rui[j - 1] * P[i]
dp[i][j] = max(dp[i][j], v)
ans = -INF
for i in range(N):
for j in range(1, N - i + 1):
ans = max(ans, dp[i][j] / bunbo[j] - penalty[j])
print(ans)
F - Apples
問題
うまくカゴをおいて、たくさんのリンゴをゲットしよう!
遅延セグメントツリーがよく分かっていない方へ
遅延セグメントツリーの記事3つ
まだ遅延セグメントツリーがよく分かってない方向けの記事をいくつか挙げています。
遅延セグメントツリーをつかった問題が解けると、そこそこパフォーマンスが盛れてうれしくなります!
考察1 (2次元平面で考える)
遅延セグメントツリーをつかって解きます。
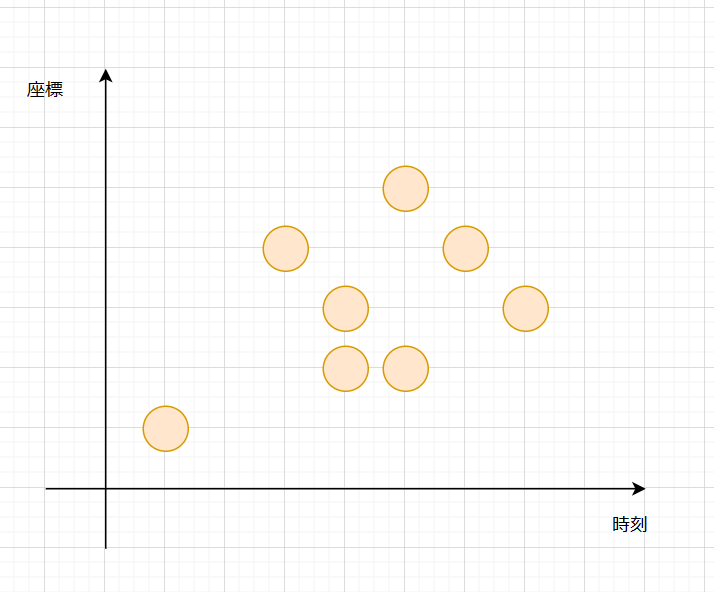
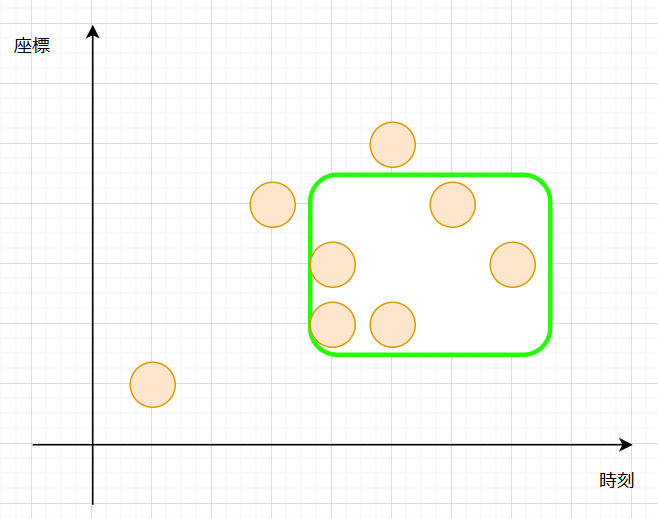
りんごの落ちてくる時刻 $t$ と座標 $x$ がたくさん与えられますが、この $2$ 変数に相関はなくて、どちらも $2\times 10^5$ 以下の範囲でいろんな入力がされます。
こういうときは、いったん $2$ 次元平面に点をプロットして、それを見ながら考えてみます。
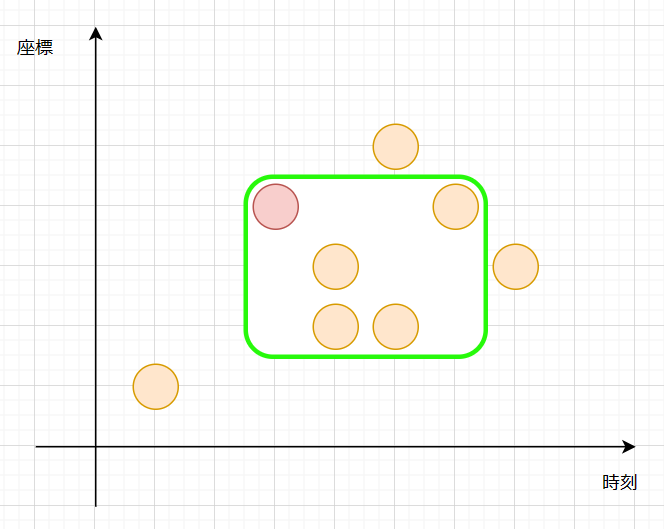
そして、時刻 $t$ について $2.5 <t < 6.5$ 、座標 $x$ について $1.5 < x < 4.5$ の範囲にあるリンゴを取るとき、 こんなイメージです。
考察2 (時刻を固定して、座標だけで考える)
$2$ 次元平面にプロットしてみたものの、やっぱり $2$ 変数を同時に扱うのはしんどいので、$1$ 変数で何とかしたいです。
なので、まずはこの小問題を考えてみます。
入力で $T$ が与えられる(今回の小問題特有の設定です)。時刻 $t$ について $T \leqq t < t+D$ の時刻に、$S$ を自由に選んで $S \leqq x <S+W$ の区間のリンゴを取れるとき、取れるリンゴの個数の最大値を求めてください。( $D$ は元の問題の入力で与えられてます)
$T=3$ が与えられたとします。
下の図の赤点にだけ注目してみます。
この赤点は、緑の枠の一番上にあってギリギリの状態です。緑枠の最も左下の座標は $(t,x)=(3,2)$ です。
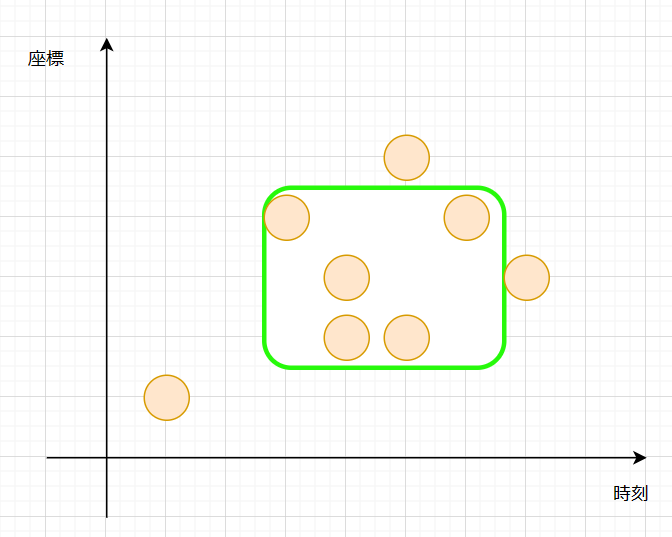
では逆に、一番下にあってギリギリの状態にしてみます。
このとき、緑枠の最も左下の座標は $(t,x) = (3, 4)$ です。
つまり、緑の枠の下面の $x$ 座標が $[2, 4]$ の範囲なら、この赤点のリンゴはゲットすることができます。
一般的に書くと、座標 $a_x$ にリンゴが落ちてくるとき、カゴの左端の座標 $x$ としたとき、カゴを $a_x-W+1 \leqq x \leqq a_x$ を満たすように置けば、そのリンゴをゲットできます。
区間全体に $+1$ するような操作です。こういう操作は遅延セグメントツリーで表せます。
座標 $a_x$ にリンゴが落ちてくるとき、 $a_x-W+1 \leqq x \leqq a_x$ の範囲の値を $+1$ すればいいです。
ゲットできるリンゴの最大値は、lazy_segtree.all_prod() で取得できます。
考察3 (時刻を動かしてみる)
さっきは $T=3$ で固定していた緑の枠を、左にずらしてみます。
$T=3$ のときの図です。この緑の枠を上下させていました。
$T=4$ のときの図です。今度はこの緑の枠を上下させたいと思っています。
$(t,x)=(3,4)$ の点が完全に外れることになりました。
また、 $(t,x)=(7,3)$ の点が新たに加わりました。
$(t,x)=(3,4)$ の点を考えなくてよくなったので、遅延セグメントツリーだと $[2,4]$ の範囲の値を $-1$ することになります。
また、新たに加わった $(t,x) = (7,3)$ の点の影響で、遅延セグメントツリーには、 $[1,3]$ の範囲の値を $+1$ することになります。
今回は点の数が少なかったですが、 $t=3$ の点の分をすべて遅延セグメントツリーから引いて、 $t=7$ の点の分をすべて遅延セグメントツリーに足します。
これを $t=0$ から順番にずらしていけばいいです。
実装については、下のコードを見てください。
コード
from atcoder.lazysegtree import LazySegTree
T_MAX = 200_003
X_MAX = 200_003
# TODO (区間演算opの単位元 op(ele1, e) = ele1)
e = 0
# 区間演算
def op(ele1, ele2):
return max(ele1, ele2)
def mapping(func, ele):
return func + ele
def composition(func_upper, func_lower):
return func_upper + func_lower
# mapping(func, ele) = ele となるようなfunc
id_ = 0
# TODO (初期リストv)
lazy_segtree = LazySegTree(op, e, mapping, composition, id_, [0] * X_MAX)
N, D, W = map(int, input().split())
G = [[] for _ in range(T_MAX)]
for _ in range(N):
t, x = map(int, input().split())
G[t].append(x)
for i in range(D):
for x in G[i]:
left = max(0, x - W + 1)
lazy_segtree.apply(left, x + 1, 1)
ans = 0
for i in range(1, T_MAX):
for x in G[i - 1]:
left = max(0, x - W + 1)
lazy_segtree.apply(left, x + 1, -1)
if i + D - 1 < T_MAX:
for x in G[i + D - 1]:
left = max(0, x - W + 1)
lazy_segtree.apply(left, x + 1, 1)
ans = max(ans, lazy_segtree.all_prod())
print(ans)