Pythonで遅延セグメントツリーの問題を解けるようにする！

はじめに

Pythonメインで書かれた遅延セグメントツリーの記事が少ないので、書いてみることにしました。
この記事では、「PythonでAtCoderにある遅延セグメントツリーの基礎的な問題が解けるようになる」ことを目標にします。

事前知識として、次のことができる前提で進めます。

• 簡単なPythonのコードが読める。 (前半部分は概論チックでPythonを知らなくても読めます)
• 普通のセグメントツリーのお気持ち・雰囲気がなんとなく分かる。

セグメントツリーの復習

セグメントツリーがどんなのだったか、いったん復習します。

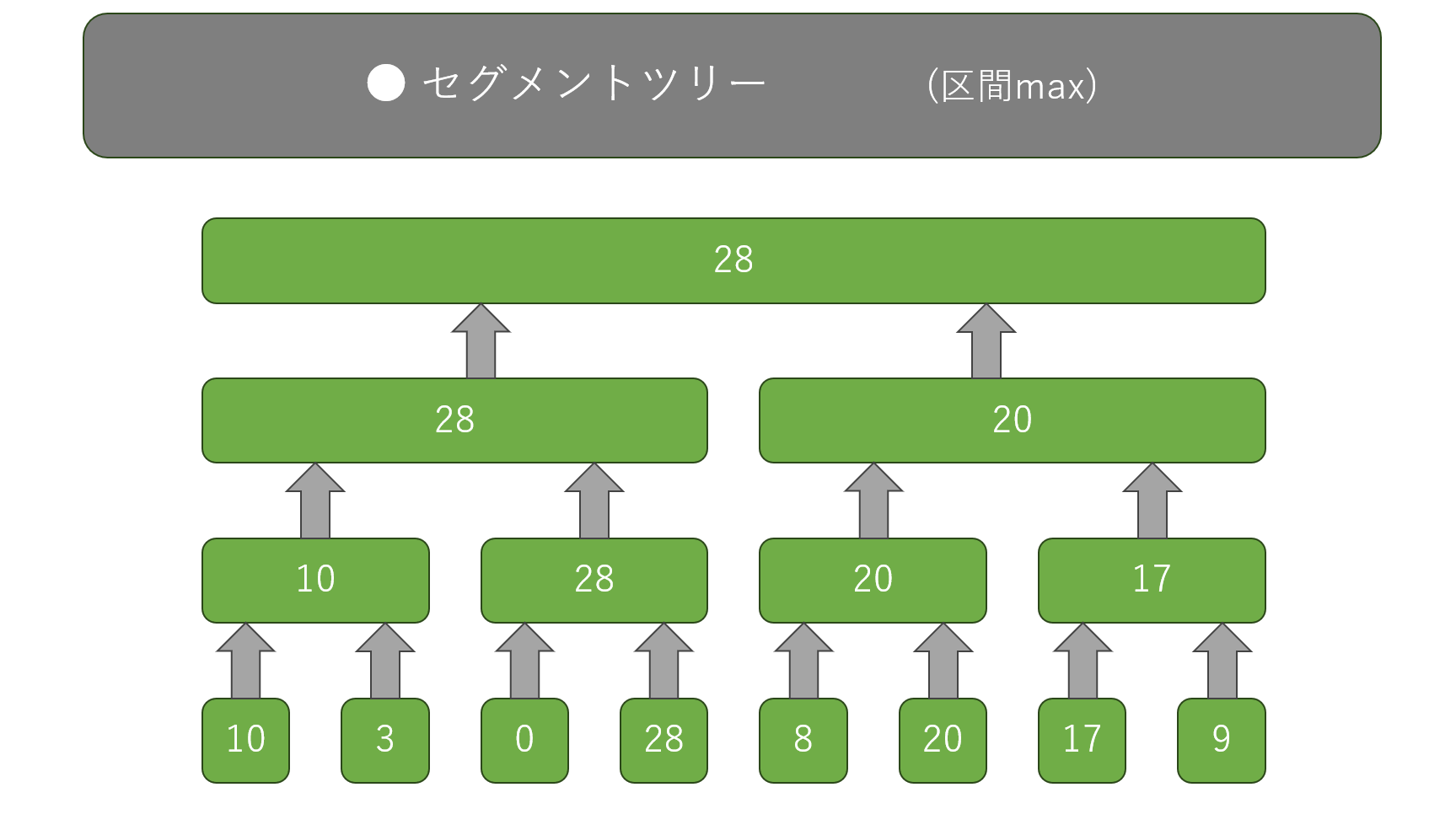
区間の最大値を求めるセグメントツリーを用意しました。

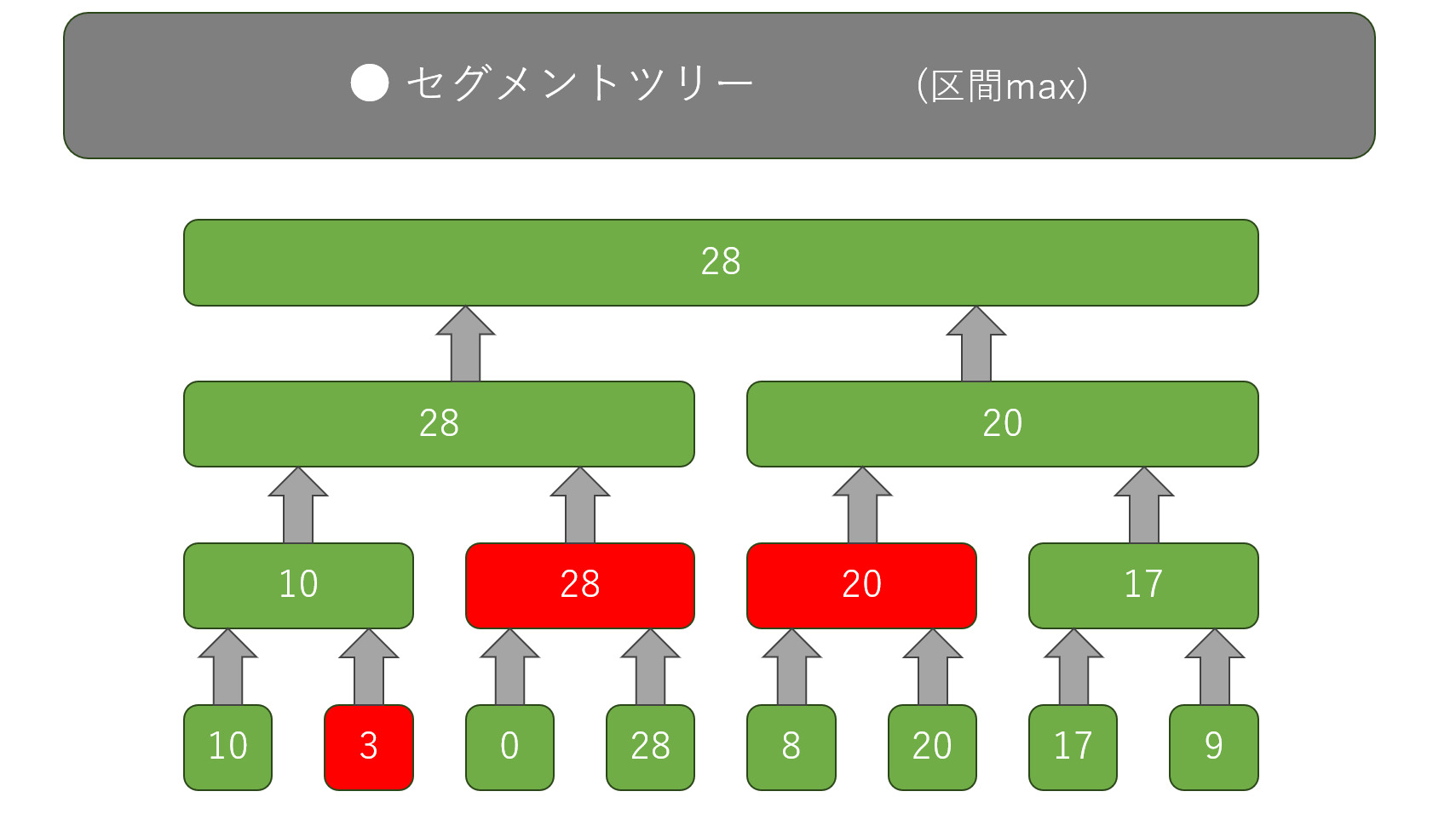
たとえば配列の $2$ ～ $6$ 番目の中の最大値を求めてくださいと言われたら...

図の赤の部分だけを見て、最大値を求めます。

また、配列の $4$ 番目の数字を $5$ に変えたいときは...

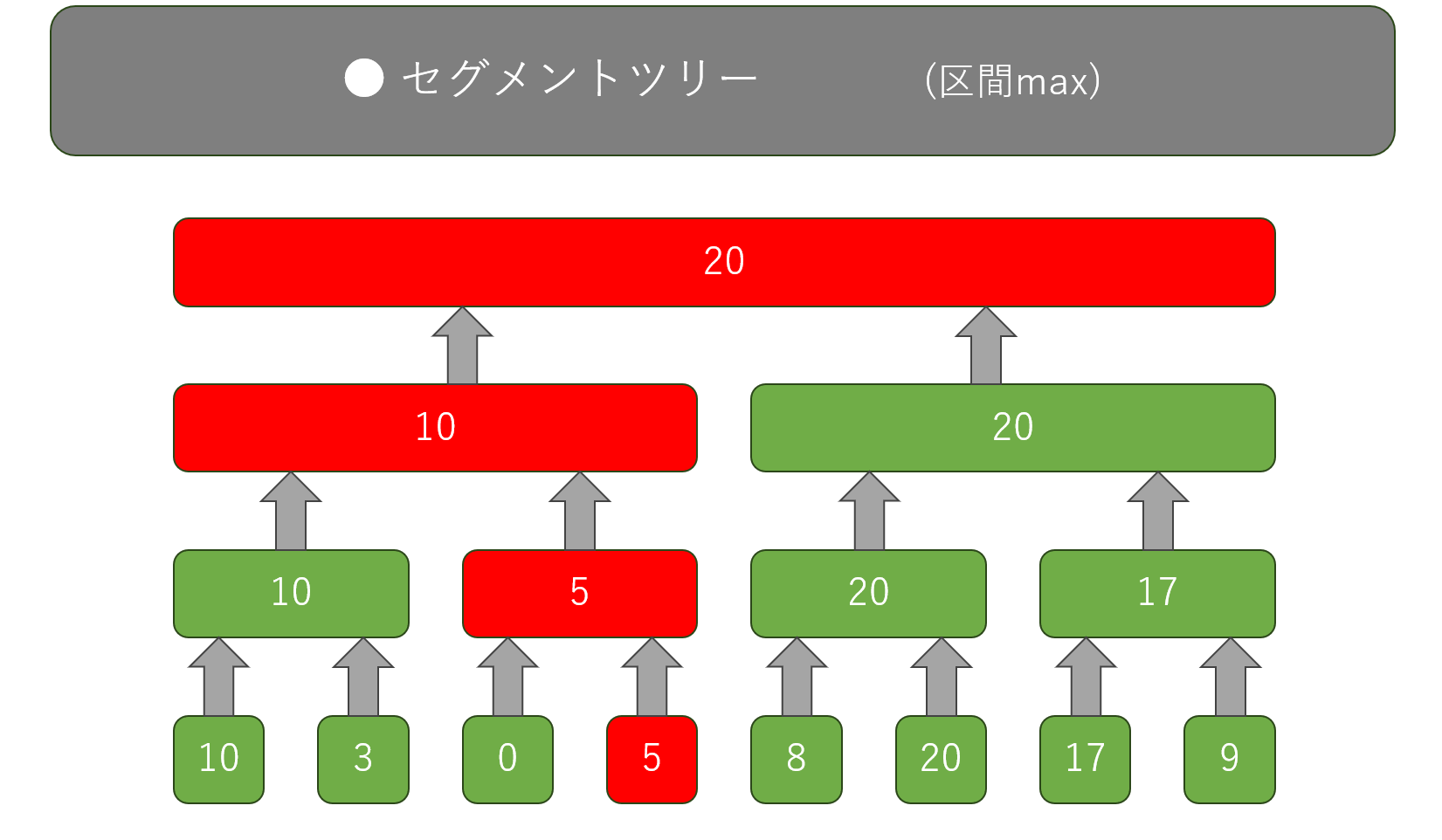
対応している葉の数字を変えて、そこから根までのノードを更新していきます。

ということで、まとめると、セグメントツリーの特徴は主に $2$ つです。

• 区間の演算が $O(logN)$ でできる。
• 値の $1$ 点更新が $O(logN)$ でできる。

では、次に遅延セグメントツリーのお話に入ります。

遅延セグメントツリーのできること

だいたい一緒です。遅延セグメントツリーのできることは主に $2$ つです。

• 区間の演算が $O(logN)$ でできる。
• 値の区間更新が $O(logN)$ でできる。

普通のセグメントツリーは、値の更新と言えば、配列のある $1$ 点だけを指して値を変更していました。
遅延セグメントツリーでは、「配列の $3$ 番目から $7$ 番目までをこんな感じで更新したい！」 みたいに、 $1$ 点だけを指さずに区間を指定して値を更新します。

区間の演算に関しては、普通のセグメントツリーと同じです。

遅延セグメントツリーのお気持ち

この問題を解きながら、遅延セグメントツリーについて見ていきましょう。

長さ $N$ の数列 $A=(A_1, A_2, \cdots ,A_N)$ が与えられます。
$Q$ 個のクエリを順に処理してください。クエリは以下の $2$ 種類です。

• 1 l r v : $i=l,l+1, \cdots ,r$ について、　$A_i \leftarrow A_i + v$
• 2 l r : $A_l, A_{l+1}, \cdots ,A_r$ の最大値を出力する。

制約1 : $1\leqq N,Q \leqq 2 \times 10^5$
制約2 : $1 \leqq A_i \leqq 10^9 (1 \leqq i \leqq N)$
制約3 : $1 \leqq v \leqq 10^9$
制約4 : $1 \leqq l,r \leqq N$

遅延セグメントツリーを用意しました。

「子が $2$ つあって、その最大値が自身の値になる」というところは、普通のセグメントツリーと全く同じです。
黄色の部分、lazyが何をするのかは、この先で説明していきます。

値の区間更新 (1)

1 l r v のクエリがとんできて、 $A_l, A_{l+1}, \cdots A_r$ それぞれについて $v$ だけ足すときに、遅延セグメントツリーではどのようなことをするのかを見ていきます。

普通のセグメントツリーの値更新は配列のある $1$ 点だけを更新するのに対して、遅延セグメントツリーでは配列のある区間の値を更新します。
たとえば、配列の $2$ ～ $4$ 番目の値に $21$ を足すとします。
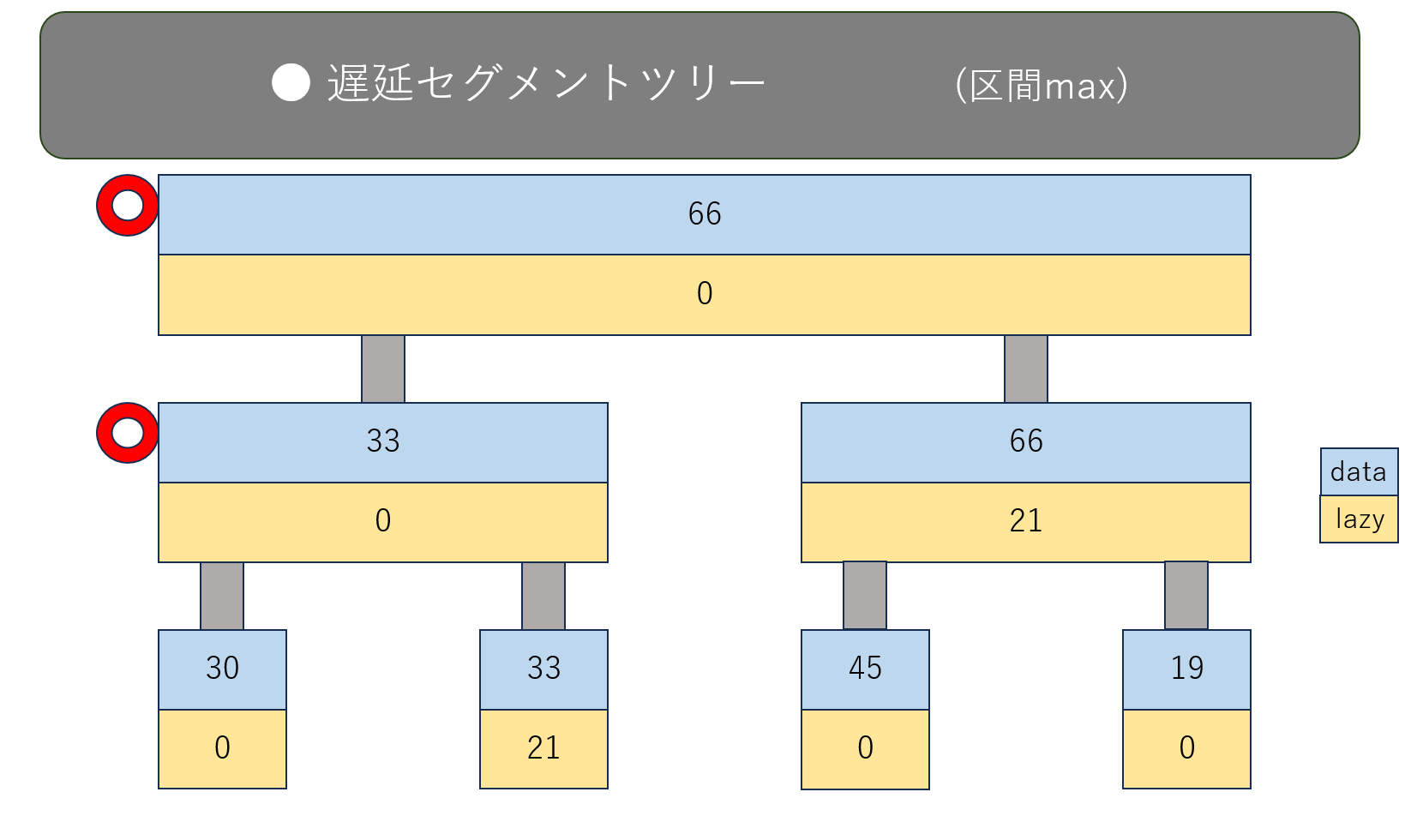
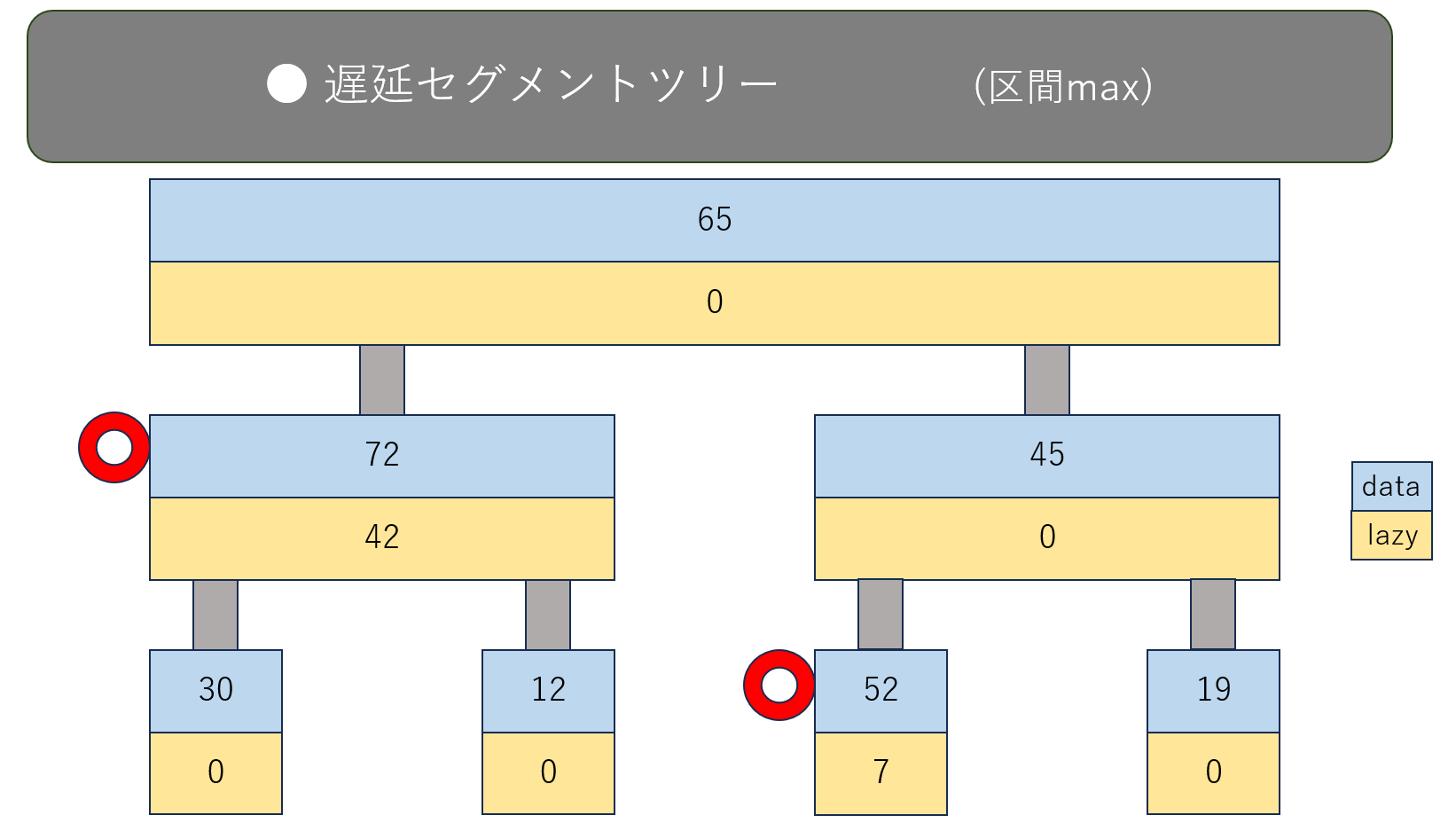
すると、遅延セグメントツリーはこうなります。(赤丸の付いたノードが変わったところです)

配列の $2$ ～ $4$ 番目に対応するノードについて、dataを $+21$ して、さらにlazyも $+21$ しています。

lazyは、「本当ならこの下のノードたちにも $+21$ したいんだけど、全部やると時間がかかるから、 下のノードたちには $+21$ をせずに一旦ここに $+21$ の情報を保持しておく」みたいな役割です。

一部のノードのdataの値が変わったので、それに伴って上側のノードも変更しておきます。

区間の演算 (1)

2 l r のクエリがとんできて、 $A_l, A_{l+1}, \cdots ,A_r$ の最大値を求めるとき、遅延セグメントツリーではどうするのかを見ていきます。

たとえば、$A_1, A_2, A_3$ の最大値を求めるとします。対応するのは矢印の付いたノードです。

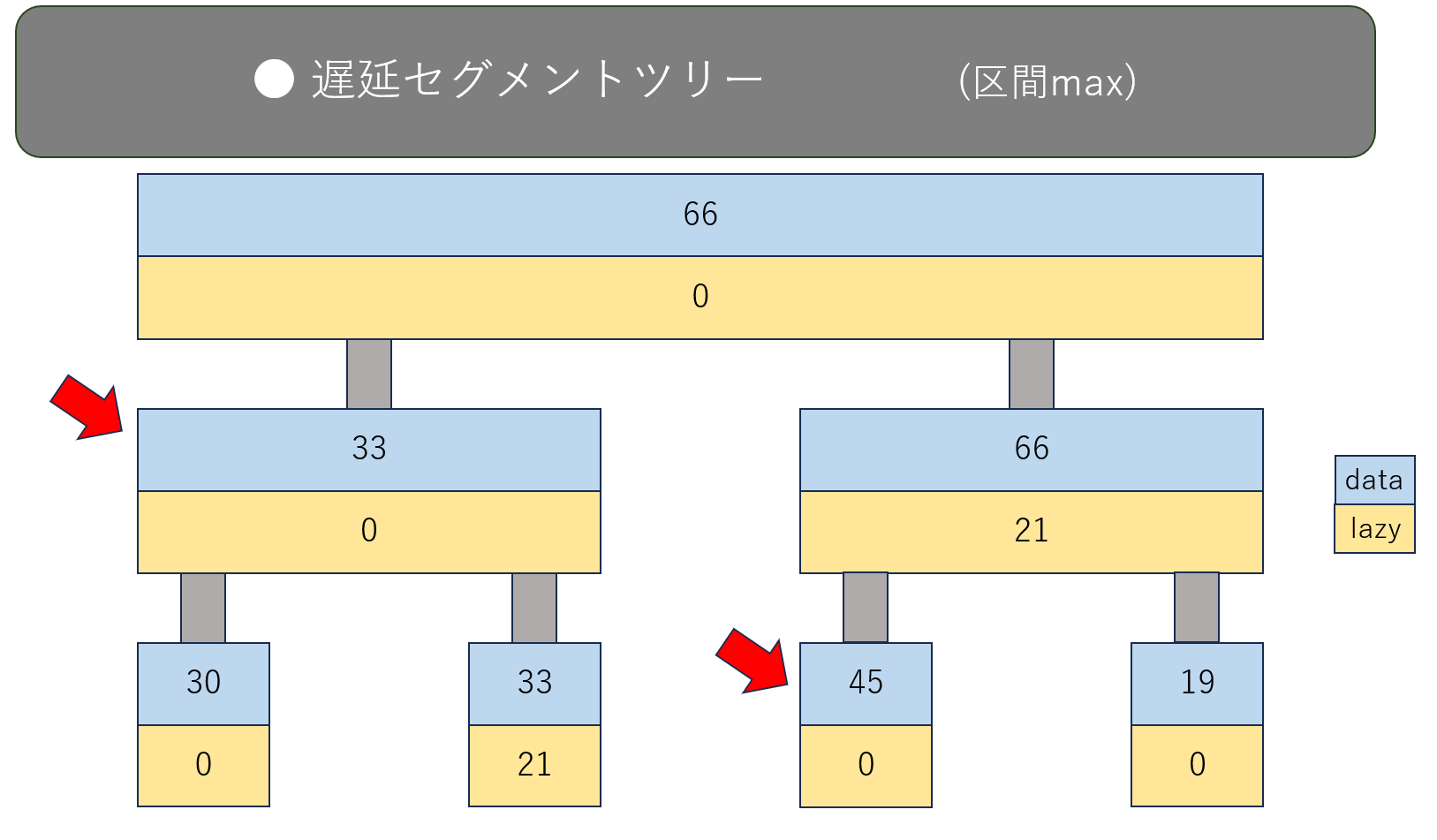
しかし、値の更新をしていた際に、本来なら足されているはずの値を上側のノードのlazyに保持したままの可能性があります。実際に、葉の右側 $2$ つ(dataが $45,19$ のノード)には本来足されているはずの $21$ が足されておらず、上のノードのlazyに $21$ がたまっています。

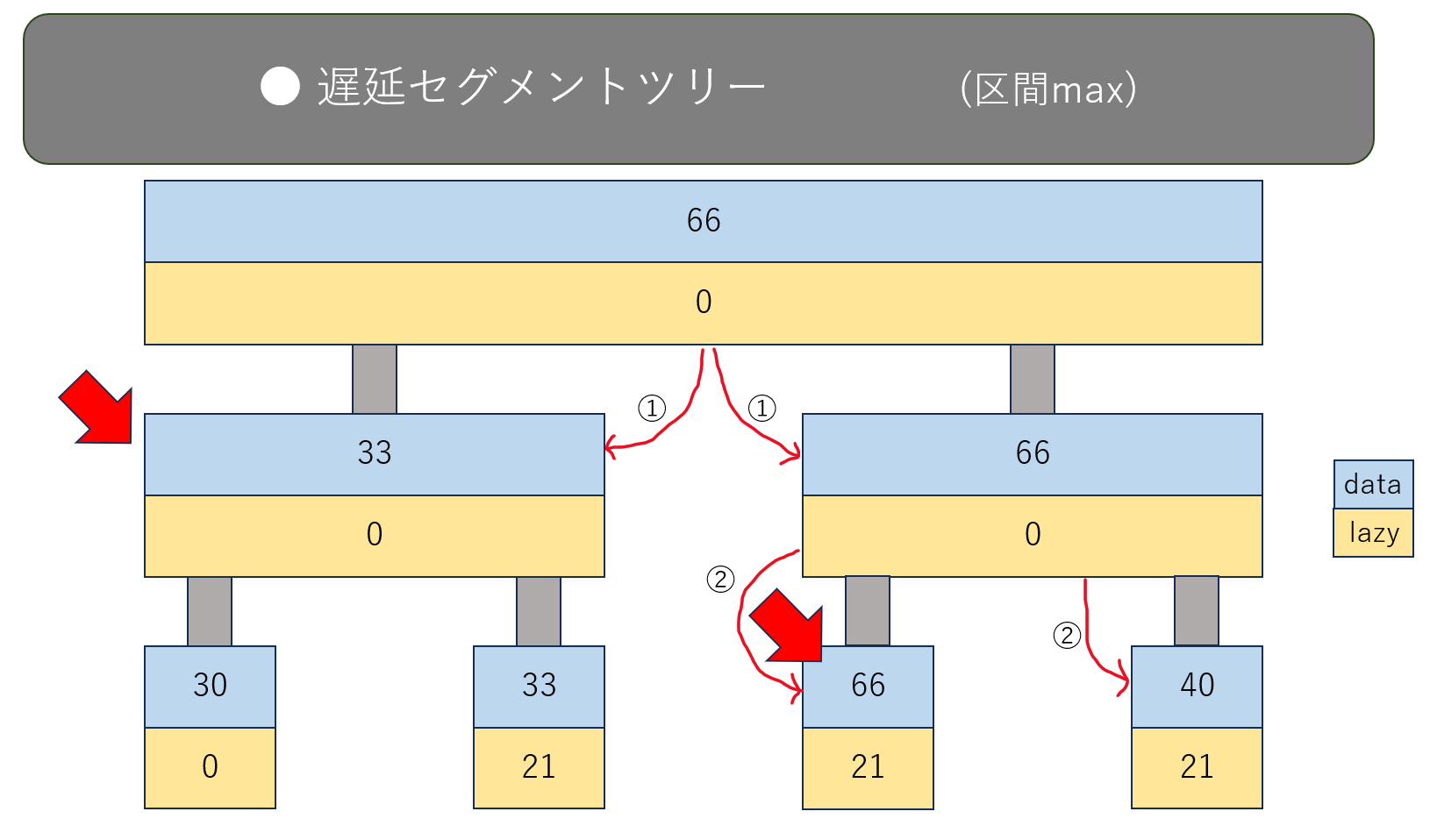
なので、いきなり赤矢印のノードを見に行かずに、こういう手順で見ていきます。

一番上の頂点(=根) から順番に、対応していたノード(赤矢印の付いていたノード)たちまで、lazyがたまってないかどうかチェックしていきます。
$1$ 番の矢印では、根のlazyの値は $0$ なので、その直下のノード $2$ つには何もしません。(lazyが $0$ なので、直下のノード $2$ つに $0$ を足したという認識でもokです)

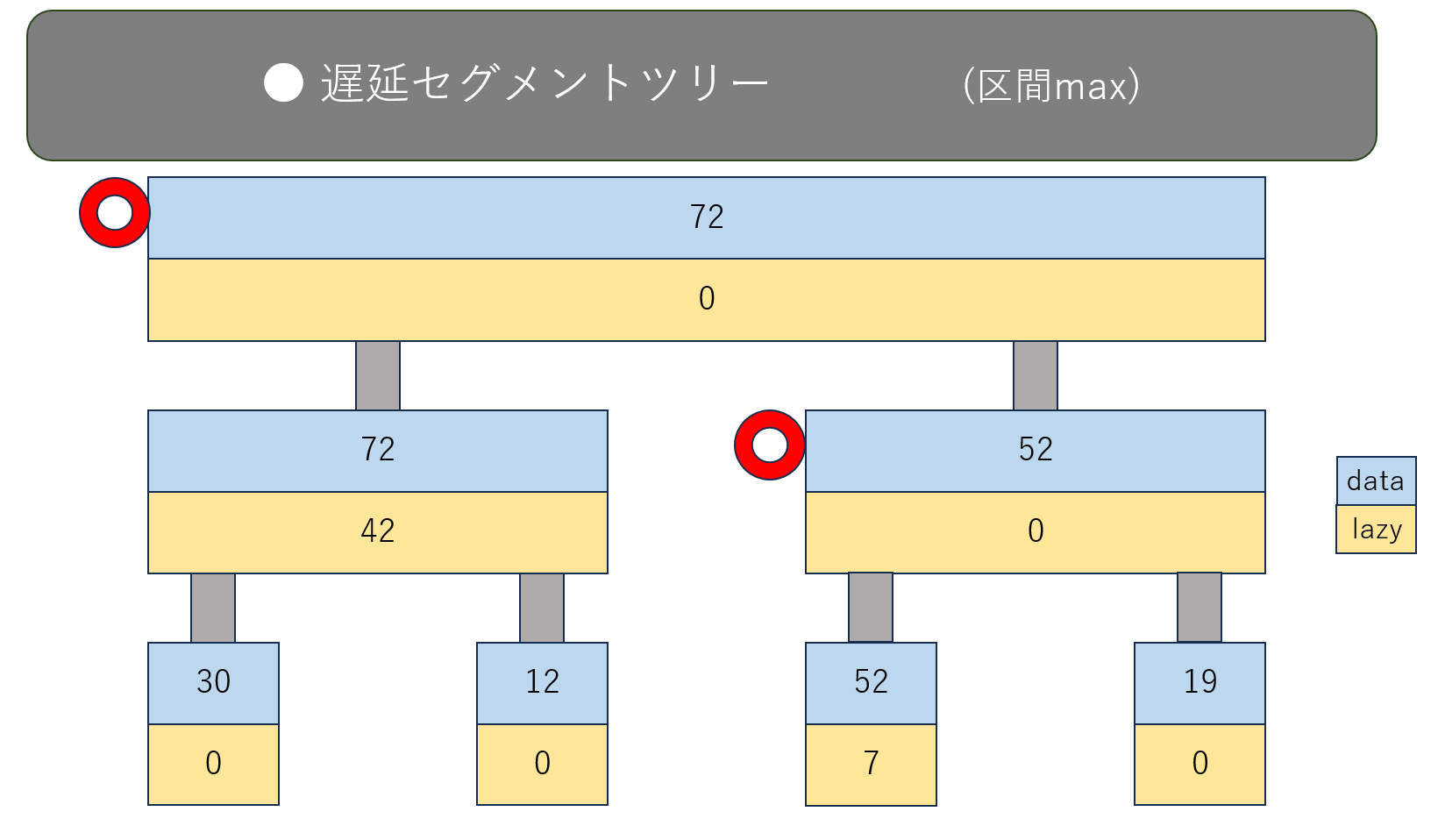
これで赤矢印の付いたノードのうち左上の方の $data=33,lazy=0$ のノードには到達できました。
まだもう片方の赤矢印の付いたノードに到達できていないので、 $2$ 番の矢印です。

$data=66,lazy=21$ のノードから直下の $2$ つのノードに向けて、$lazy=21$ を反映させます。
具体的には、直下のノードのdataに $+21$ をして、直下のノードのlazyにも $+21$ をします。
今回は画像サイズの都合で $3$ 段の遅延セグメントツリーしか用意できてませんが、この下側にもまだノードがあるときを想像してもらえると、直下のノードのlazyも変更しないといけないのが分かるかと思います。
これで赤矢印の付いたノードすべてについて上側にあるlazyはすべて反映済みになり、赤矢印の付いたノードのdataはすべて正しい値になりました。

$A_1,A_2,A_3$ の最大値は、赤矢印の付いたノードのdataだけに注目して、 $\max(33,66)=66$ だと計算することができました。

値の区間更新 (2)

1 l r v のクエリが連続してたくさん飛んでくるときを考えます。
ゴチャついてきていたので、遅延セグメントツリーを元に戻しておきました。この図を基準に考えていきます。

まず、$l=1,r=2,v=35$ のクエリがとんできたとします。(赤丸の付いたノードが更新したノードです)

上側のノードのdataも変更です。

次に、 $l=1,r=3,v=7$ のクエリがとんできたとします。

対応するノードのdataに $+7$ すると同時に、lazyにも $+7$ します。
lazyに $0$ 以外の値が入っていても同じです。

上側のノードのdataも変更です。

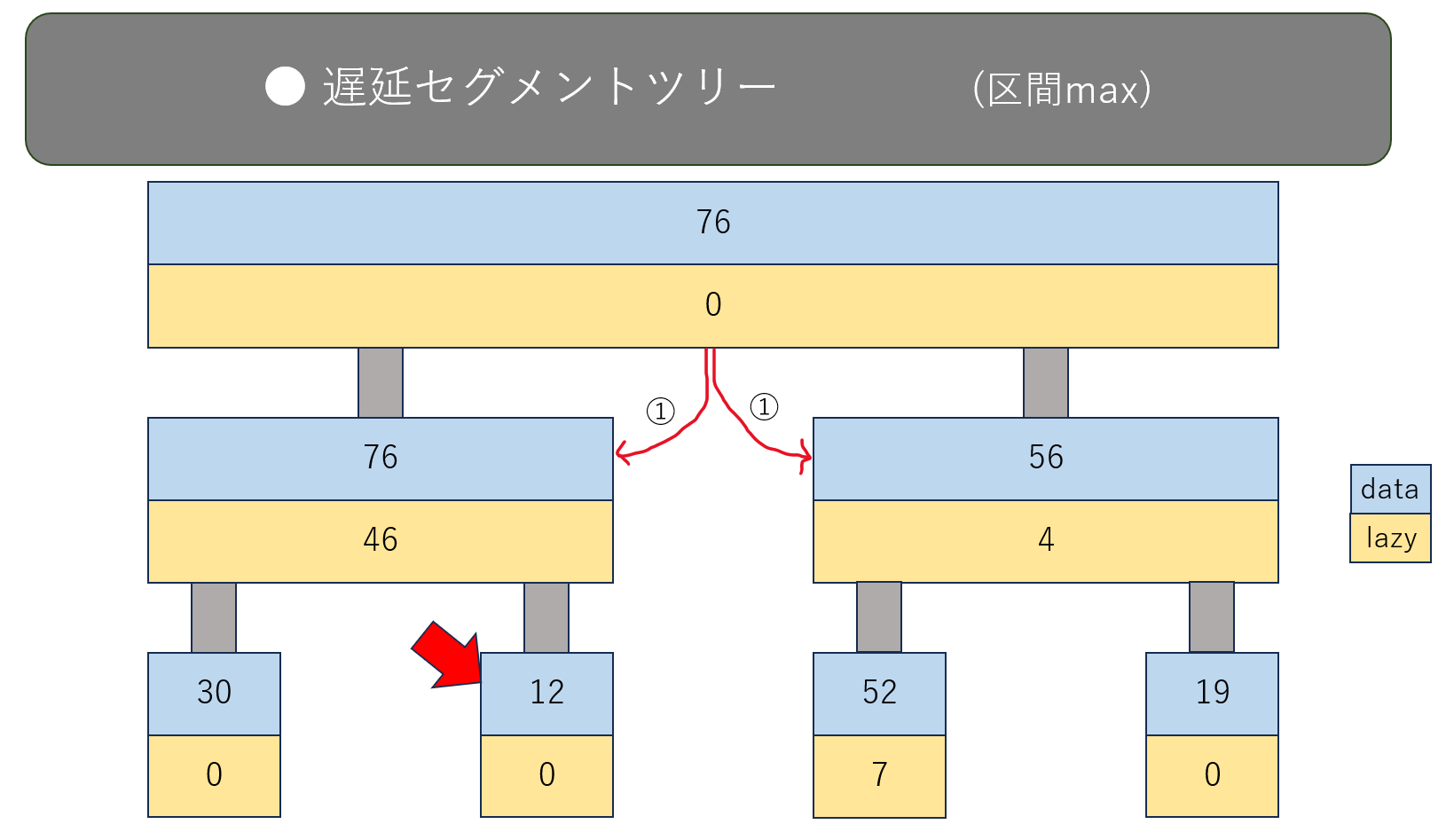
最後に、 $l=1,r=4,v=4$ のクエリがとんできたとします。

区間の演算 (2)

たとえば、 $A_2$ の値が知りたいとします。
対応するノードは、次の図の赤矢印の付いたノードです。

ここには真の値は入っていなくて、上側にたまっているlazyをちゃんと反映させないといけないのでした。
ということで、一番上の頂点(=根)から順番に見ていきます。

根にあった $lazy=4$ を直下のノード $2$ つに反映させます。
dataを $+4$ するのはもちろん、lazyにも $+4$ します。これはlazyの値が $0$ でなくても同じです。
まだ赤矢印の付いたノードに到達できていないので、さらに下に行きます。

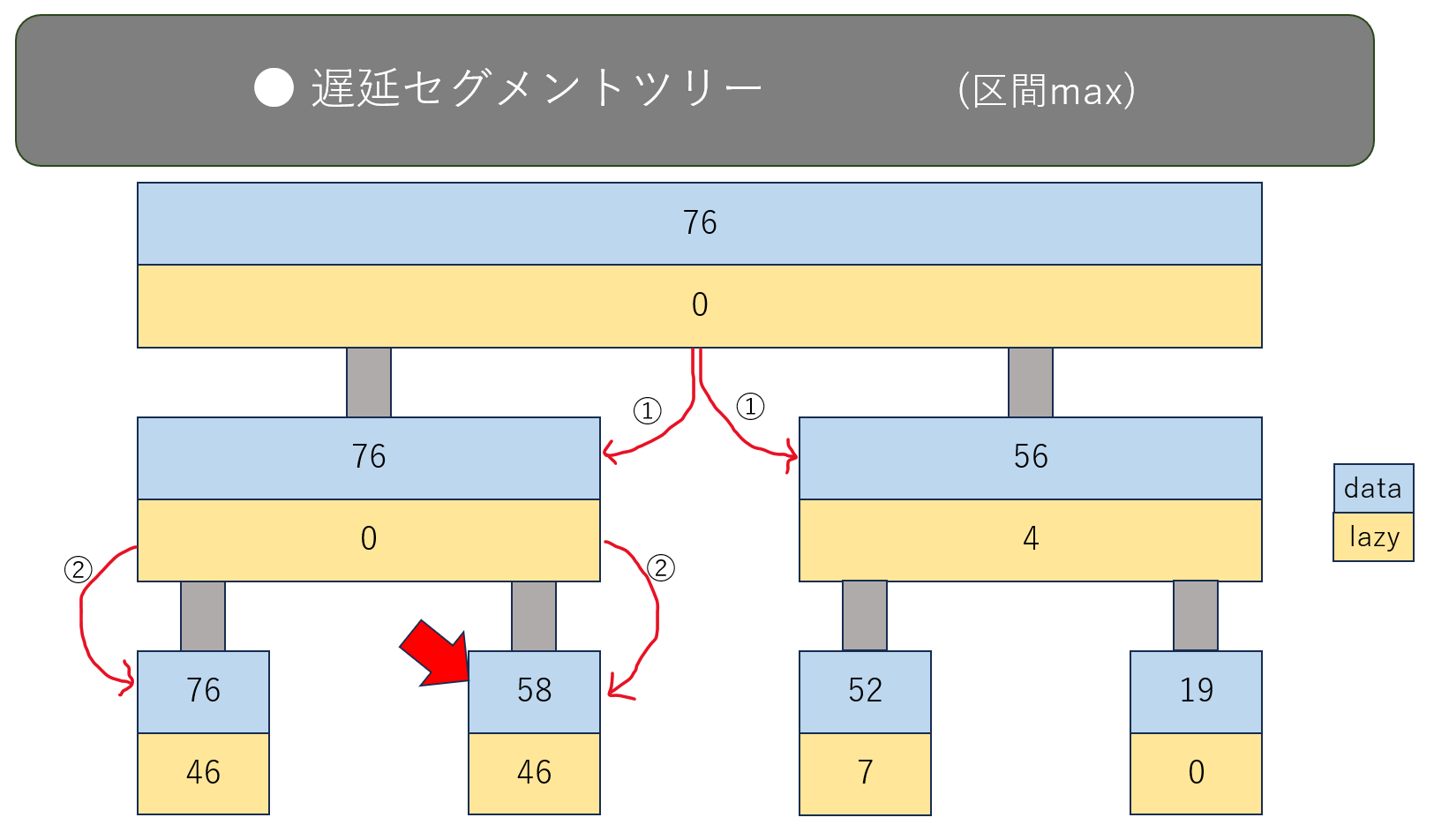
これで $A_2=58$ だと分かりました。

Pythonで書いてみる

ここまで、遅延セグメントツリーのなんとなくの動き方をシミュレーションしてきました。
ここからは、それをもとに、Pythonで問題を解けるようにしていきます。

問題を解くのが目標なので、遅延セグメントツリー自体は他の人から拝借します。
今回は、ac-library-pythonにある遅延セグメントツリー(これ)を使うことにします。 ac-library-pythonを自分のPCでつかえるようにする方法は、私の過去の記事 (これ) に書いてあります。

ざっくりとしたつかい方は、こうです。

from atcoder.lazysegtree import LazySegTree

lazy_segtree = LazySegTree(op, e, mapping, composition, id_, v)

引数が $6$ つあります。これをうまく設定すると動いてくれます。
1つ1つ何を設定するのかを見ていきます。

op: 区間の演算

これは普通のセグメントツリーと同じです。
区間の最大値を計算したいのであれば $\max$ を設定するし、最小公倍数lcmや排他的論理和xorも設定できます。
たとえば、排他的論理和xorを設定したいなら、こう書けばいいです。

def op(data1, data2):
    return data1 ^ data2

e: opの単位元

単位元というとややこしいですが、こういう性質のものです。
$$op(data1, e) = data1$$
たとえば、opが最大値maxであれば、$e=-∞$　とすればいいですし、opが排他的論理和xorであれば、 $e=0$ とすればいいです。
演算しても全く意味のないものが $e$ です。

mapping: 上のlazyを下のdataに作用させる

この状態の遅延セグメントツリーで、赤矢印の付いたノードを見たいとき、根から順番に辿ってlazyがないかチェックするのでした。

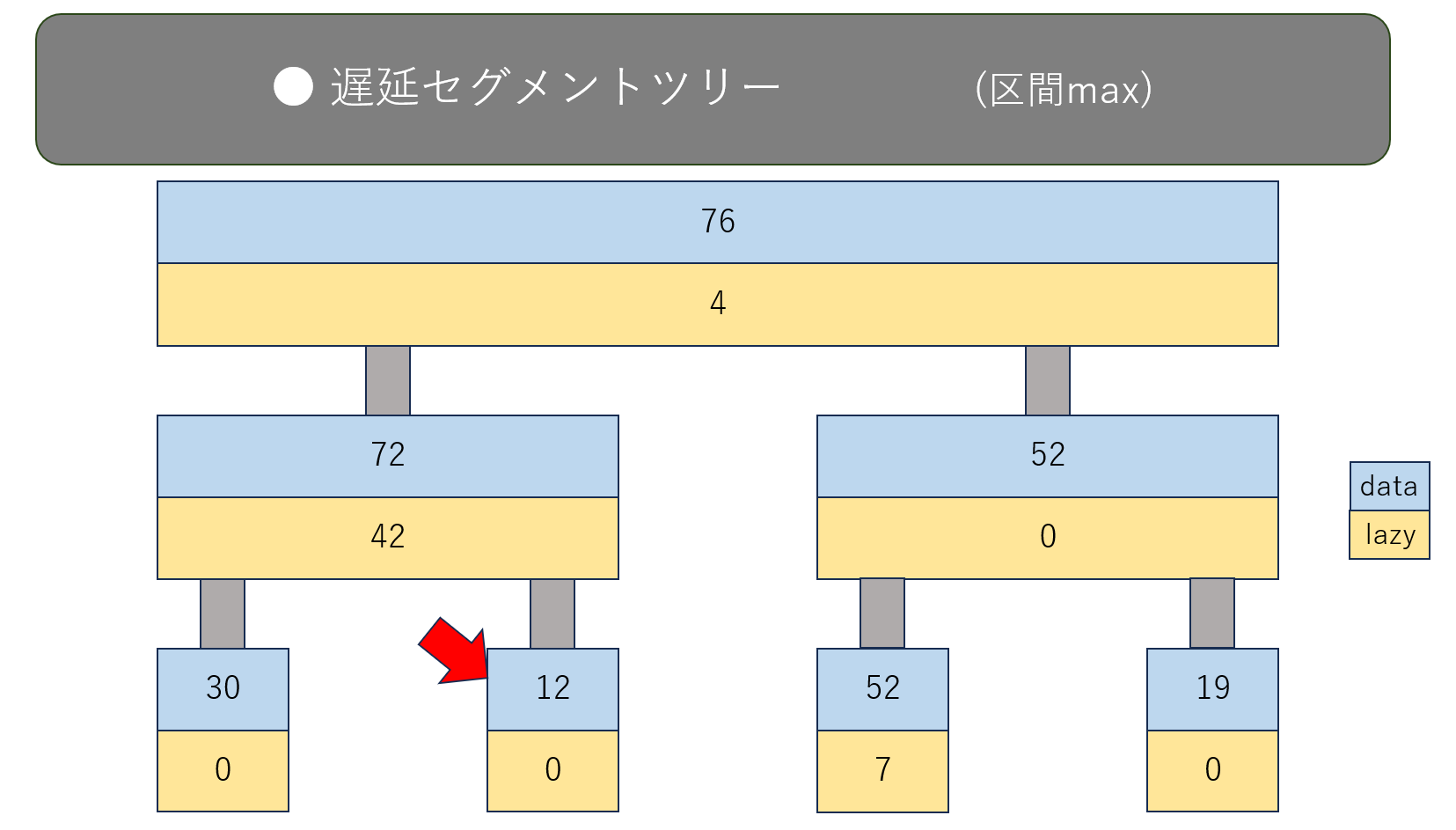
根からその直下のノード $2$ つにlazyを作用させた結果がこうです。

根にあった $lazy=4$ を直下のノードのdataに作用させました。
この例では足し算するだけです。なので、mappingは次のように書きます。

def mapping(lazy_upper, data_lower):
    return data_lower + lazy_upper

composition: 上のlazyを下のlazyに作用させる

先ほど貼り付けた遅延セグメントツリーの例では、上側のlazyの影響で下側のdataを変えただけではなく、下側のlazyも変わっていました。
この例では $2$ つのlazy同士を足し算するだけです。Pythonではこう書きます。

def composition(lazy_upper, lazy_lower):
    return lazy_upper + lazy_lower

_id: mappingの恒等写像

恒等写像というとややこしいですが、こういう性質のものです。
$$mapping(data, id) = data$$
mapping関数のlazyの部分に入れて、そのままのdataが返ってくるものが_idです。

v: 初期リスト

そのまま初期リストです。

問題を解いてみる (1)

(問題の再掲です)

長さ $N$ の数列 $A=(A_1, A_2, \cdots ,A_N)$ が与えられます。
$Q$ 個のクエリを順に処理してください。クエリは以下の $2$ 種類です。

• 1 l r v : $i=l,l+1, \cdots ,r$ について、　$A_i \to A_i + v$
• 2 l r : $A_l, A_{l+1}, \cdots ,A_r$ の最大値を出力する。

制約1 : $1\leqq N,Q \leqq 2 \times 10^5$
制約2 : $1 \leqq A_i \leqq 10^9 (1 \leqq i \leqq N)$
制約3 : $1 \leqq v \leqq 10^9$
制約4 : $1 \leqq l,r \leqq N$

ここまで書いてきたのをまとめると、こう書けます。

from atcoder.lazysegtree import LazySegTree


# 区間演算op
def op(data1, data2):
    return max(data1, data2)


# opの単位元 op(data1, e) = data1
e = -float("Inf")


# lazyをdataに作用させる
def mapping(lazy_upper, data_lower):
    return data_lower + lazy_upper


# lazyをlazyに作用させる
def composition(lazy_upper, lazy_lower):
    return lazy_upper + lazy_lower


# mapping(_id, data_lower) = data_lower
_id = 0

N = int(input())
A = list(map(int, input().split()))

lazy_segtree = LazySegTree(op, e, mapping, composition, _id, A)

Q = int(input())
for _ in range(Q):
    t, *q = map(int, input().split())
    match t:
        case 1:
            l, r, v = q
            lazy_segtree.apply(l - 1, r, v)
        case 2:
            l, r = q
            ans = lazy_segtree.prod(l - 1, r)
            print(ans)

問題を解いてみる (2)

典型90問の中にある、遅延セグメントツリーの問題を解いてみます。

問題要約

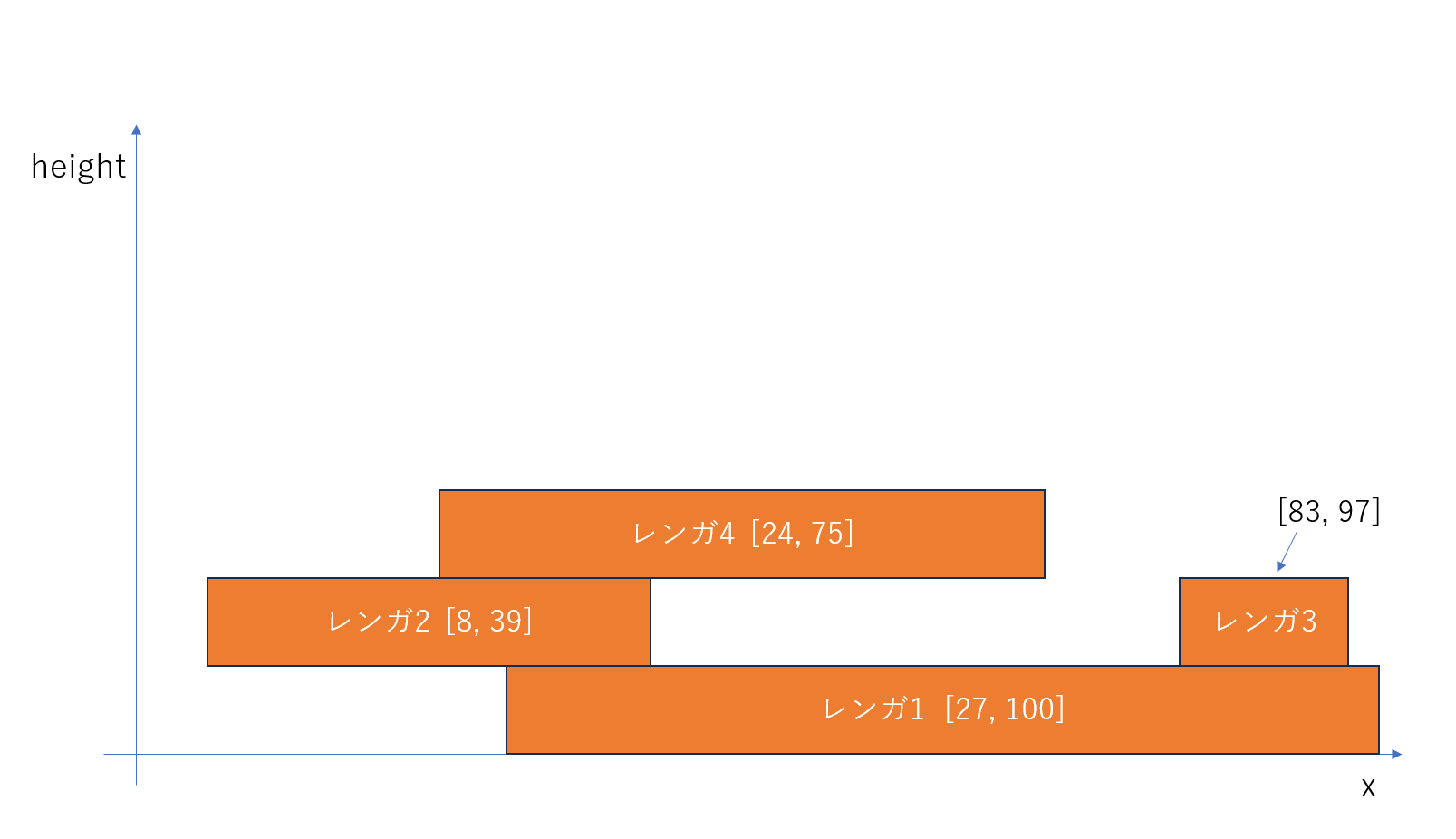
数直線上にレンガを積み上げていきます。
$i$ 番目のレンガは、 $l_i \leqq x \leqq r_i$ の範囲に積み上げます。
それぞれのレンガについて、高さを出力してください。

シミュレーションする

入力例 $1$ はこのような図になります。

方針

$i$ 番目のレンガを積み上げるとき、 $l_i \leqq x \leqq r_i$ の区間の値の最大値を求めます。
その値に $+1$ したのが、 $i$ 番目のレンガの高さです。

引数を設定する

最初に図解していた遅延セグメントツリーでは、1 l r v のクエリで、配列の$l$ 番目から $r$ 番目まで $v$ を足していました。
今回は、指定した区間に $v$ を足すのではなく、指定した区間の値を一律に $v$ (=レンガの高さ)にしたいです。
なので、設定する引数も先ほどと少し変わってきます。

先に初期リストは、長さ $W$ で値がすべて $0$ の配列を用意すればいいです。この値はレンガの高さに対応しています。

# 初期リスト
lst = [0] * W

区間の演算では、指定した区間の値の最大値(=区間内のレンガの高さの最大値)を求めます。

# 区間演算op
def op(data1, data2):
    return max(data1, data2)

# opの単位元 op(data1, e) = data1
e = -1

lazyは、その区間全体に高さlazyのレンガが積まれていることを意味するとします。
何もなければ基本的には $lazy=-1$ で、たとえばあるノードのlazyの値が $3$ のとき、その下のノードのdataも $3$ にしないといけないけれど、いったんlazyにその情報をためているイメージです。

# lazyをdataに作用させる
def mapping(lazy_upper, data_lower):
    if lazy_upper == -1:
        return data_lower
    else:
        return lazy_upper


# lazyをlazyに作用させる
def composition(lazy_upper, lazy_lower):
    if lazy_upper == -1:
        return lazy_lower
    else:
        return lazy_upper


# mapping(_id, data_lower) = data_lower
_id = -1

これで引数 $6$ つをすべて設定できました。
まとめると、以下のコードになります。

解答コード例 (長いので折りたたみ)

from atcoder.lazysegtree import LazySegTree

W, N = map(int, input().split())

# 初期リスト
lst = [0] * W


# 区間演算op
def op(data1, data2):
    return max(data1, data2)


# opの単位元 op(data1, e) = data1
e = -1


# lazyをdataに作用させる
def mapping(lazy_upper, data_lower):
    if lazy_upper == -1:
        return data_lower
    else:
        return lazy_upper


# lazyをlazyに作用させる
def composition(lazy_upper, lazy_lower):
    if lazy_upper == -1:
        return lazy_lower
    else:
        return lazy_upper


# mapping(_id, data_lower) = data_lower
_id = -1

lazy_segtree = LazySegTree(op, e, mapping, composition, lst)

for _ in range(N):
    l, r = map(int, input().split())
    l -= 1
    max_height = lazy_segtree.prod(l, r)
    lazy_segtree.apply(l, r, max_height + 1)
    print(max_height + 1)

問題を解いてみる (3)

最後に、AtCoder Library Practice Contest の中にある、遅延セグメントツリーの問題を解いてみます。

問題要約

数列 $A=(a_0,a_1, \cdots , a_{N-1})$ が与えられます。$Q$ 個のクエリを順番に処理してください。クエリは $2$ 種類あって、以下の通りです。
0 l r b c : $i=l,l+1, \cdots r-1$ について、$a_i \leftarrow b \times a_i + c$
1 l r : $\sum_{i=l}^{r-1} a_i$ (mod $998244353$ ) を出力する。

dataとlazyをどうするか

実は、今までのやり方だとうまくいきません。
天下り的になるんですが、dataには対応している区間の値の総和だけではなく、その区間の長さも必要です。要するに、(対応している区間の値の総和, 対応している区間の長さ) のタプルを dataとします。
dataやlazyは整数でもいいし、タプルでもいいし、なんなら自作のクラスでもいいわけです。

引数を設定する

ということで、LazySegTreeに入れる $6$ つの引数を設定していきます。

dataには、(対応する区間の値の総和, 対応する区間の長さ) のタプルが入ります。

# 区間の演算op
def op(data1, data2):
    sum1, length1 = data1
    sum2, length2 = data2
    next_sum = (sum1 + sum2) % MOD
    next_length = length1 + length2
    return (next_sum, next_length)

# opの単位元 op(data1, e) = data1
e = (0, 0)

lazyには $(b,c)$ のタプルを入れます。
たとえば、 $(a_0,a_1,a_2,a_3)$ の $4$ 要素それぞれに $a_i \leftarrow b \times a_i+c$ をすると、
$(a_0,a_1,a_2,a_3) \leftarrow (b \times a_0+c,b \times a_1+c,b \times a_2+c, b \times a_3+c)$ となり、その総和は $b \times (a_0+a_1+a_2+a_3) + c \times 4$ です。
$(a_0+a_1+a_2+a_3)$ の部分は、 $[0,3]$ の区間に対応するノードのdataの値です。
$c \times 4$ の $4$ の値は、 $[0,3]$ の区間の長さのことです。

これをPythonで書くと、次のようになります。

# lazyをdataに作用させる
def mapping(lazy_upper, data_lower):
    b, c = lazy_upper
    sum1, length1 = data_lower
    next_sum = (b * sum1 + c * length1) % MOD
    return (next_sum, length1)

# mapping(_id, data_lower) = data_lower
_id = (1, 0)

$a_i \leftarrow b_1 \times a_i+c_1$ の変換をした後、さらに $a_i \leftarrow b_2 \times a_i+c_2$ の変換をするときを考えます。
この $2$ つの操作をまとめると、 $a_i \leftarrow b_2 \times(b_1 \times a_i + c_1) + c_2 = b_1b_2 \times a_i + (b_2c_1+c_2)$ となります。
これがcompositionにあたります。

# lazyをlazyに作用させる
def composition(lazy_upper, lazy_lower):
    b2, c2 = lazy_upper
    b1, c1 = lazy_lower
    next_b = b1 * b2 % MOD
    next_c = (b2 * c1 + c2) % MOD
    return (next_b, next_c)

最初のリストは、dataが(対応している区間の値の総和, 対応している区間の長さ) のタプルなので、次のように設定します。

A = list(map(int, input().split()))
lst = [(a, 1) for a in A]

これで遅延セグメントツリーをつくれました。
解答コードは以下の通りです。

解答コード例 (長いので折りたたみ)

from atcoder.lazysegtree import LazySegTree

MOD = 998244353

N, Q = map(int, input().split())
A = list(map(int, input().split()))


# 区間の演算op
def op(data1, data2):
    sum1, length1 = data1
    sum2, length2 = data2
    next_sum = (sum1 + sum2) % MOD
    next_length = length1 + length2
    return (next_sum, next_length)


# opの単位元 op(data1, e) = data1
e = (0, 0)


# lazyをdataに作用させる
def mapping(lazy_upper, data_lower):
    b, c = lazy_upper
    sum1, length1 = data_lower
    next_sum = (b * sum1 + c * length1) % MOD
    return (next_sum, length1)


# mapping(_id, data_lower) = data_lower
_id = (1, 0)


# lazyをlazyに作用させる
def composition(lazy_upper, lazy_lower):
    b2, c2 = lazy_upper
    b1, c1 = lazy_lower
    next_b = b1 * b2 % MOD
    next_c = (b2 * c1 + c2) % MOD
    return (next_b, next_c)


lst = [(a, 1) for a in A]

lazy_segtree = LazySegTree(op, e, mapping, composition, _id, lst)

for _ in range(Q):
    t, *q = map(int, input().split())
    match t:
        case 0:
            l, r, b, c = q
            lazy_segtree.apply(l, r, (b, c))
        case 1:
            l, r = q
            ans = lazy_segtree.prod(l, r)[0]
            print(ans)

最後に

ここまで読んでくださってありがとうございました。

ここで取り扱った問題たちはどれも基礎的な問題で、遅延セグメントツリーの難しいところは「dataやlazyをどう設定するか」につきます(たぶん)。

あと、遅延セグメントツリーは定数倍がとても重くて、Pythonだと想定解通りでも実行制限時間に間に合わない悲しいケースもあります。なるべく計算が軽くなるような工夫をするようにしましょう。