前回のおさらい
前回は公称寿命を超えるストレス試験を行った対象機械の振動データを用いて、故障予知診断を試みました。そこでは十分な数の異常データも入手できましたので、一般的な機械学習の分類器であるSVMモデルで正常と異常データの分類の行うことができました。しかしながら実際の故障予知診断の現場では、多数かつ多様な異常データを入手できることはほとんどありません。ここが、異常データは宝物といわれる所以です。
異常検知の世界
英語でAnormaly Detectionと呼ばれる異常検知を目的とする機械学習の研究分野は、少し特殊で残念ながら研究者も必ずしも多くありませんが、近年製造業をはじめとする産業界からの強いニーズで徐々に研究が進んできました。この世界の前提は、多量の正常データ(あるいはごく少量の異常データを含む正常データ)のみから作る予測モデルで”まだ見ぬ異常値を検出するというものです。一般的に異常検知で想定される異常状態は、複数の要因で誘発される異なる特徴の外れ値ですから、少数の異常値があったとしてもそれを機械学習的なアプローチで”膨らませて”一般的なクラス分類器の問題に落とそうとすると失敗するようです。
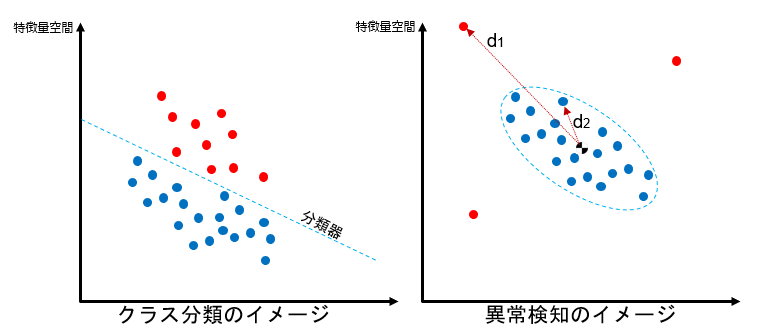
今回試すアプローチは、右の図のように正常値データ群から形成されるクラスタを定義し、そこからの外れ具合を測る距離で異常値を検出します。矛盾するようですが、最終的なモデル精度を検証するには異常値をモデルに入れてみてきちんと異常値として判定されることを確認するしかありません。実際の現場では、1台の対象機械を実際壊したりして最後の検証を行います。
マハラノビス・タグチ法
伝統的な多変量解析で有名な概念にマハラノビス距離というものがあり、最新のニューラルネットワーク理論等でも重要な概念になっています。今回はマハラノビス距離を使った異常検知の元祖であるマハラノビス・タグチ法(以後MT法)あるいはホテリングT2法として知られる手法をご紹介したいと思います。
マハラノビス距離の概念は難しくありません。受験シーズンなので試験に例えると偏差値という概念がイメージが近いです。難易度や満点が異なる試験結果をそのまま比較するのはもちろん意味がありません。また難易度=平均点が同じ試験であっても大多数が平均点付近だった試験と、点数がばらけた試験を同列に扱うと後者の試験で高得点だった人が圧倒的に有利になってしまいます。マハラノビス距離は乱暴に言うと多変数(機械学習では複数特徴量)の各分布から平均を引いて標準偏差で割ることにより正規化した上で、クラスタ中心からの距離を算出する手法です。平均を0とし分散の大きな特徴量の影響力を抑え、分散の小さな特徴量の影響を拡大します。理論的な説明は、以下のサイト・書籍が詳しいです。
https://qiita.com/MasafumiTsuyuki/items/2677576849abf633e412
https://www.amazon.co.jp/gp/product/4061529080/ref=ppx_yo_dt_b_asin_title_o00_s00?ie=UTF8&psc=1
MT法は医療分野(画像から異常部位を検出する)や品質管理の分野で長い歴史と実績があります。数多くの応用論文がネット上に出ていますので、ご興味がある方はそちらも参考にしてください。
特徴量の抽出
今回も前回同様回転機の加速度振動データがスタートですが、データ量が多量(千件以上)なのと異常データが含まれないという点が異なります(どちらもMT法がうまくいくためのするための重要な要件になります)。
前回はFFTを64分割しましたが64特徴量でMT法は複雑すぎるのでFFTは16分割とし、時系列の加速度データの実効値(RMS)平均、波高率(実効値の最大値/実効値の平均)、さらにエンベロープ処理結果のスペクトル値上位2つという組み合わせで特徴量を形成します。
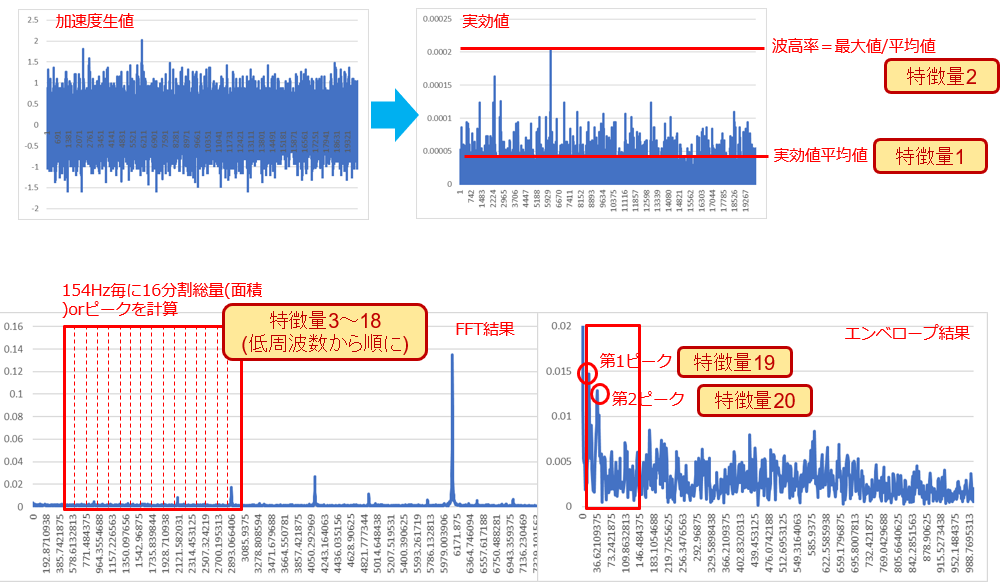
繰り返しになりますが、特徴量はオペレーションの知見から試行錯誤しながら選びます。特徴量が対象の正常or故障をうまく表現できなければ、どんな推定モデルを作ってもうまくいきません。ですから、実際は特徴量選定→モデル作成→評価→特徴量選定...と繰り返して歓喜の瞬間を待つことになります。
特徴量の分布
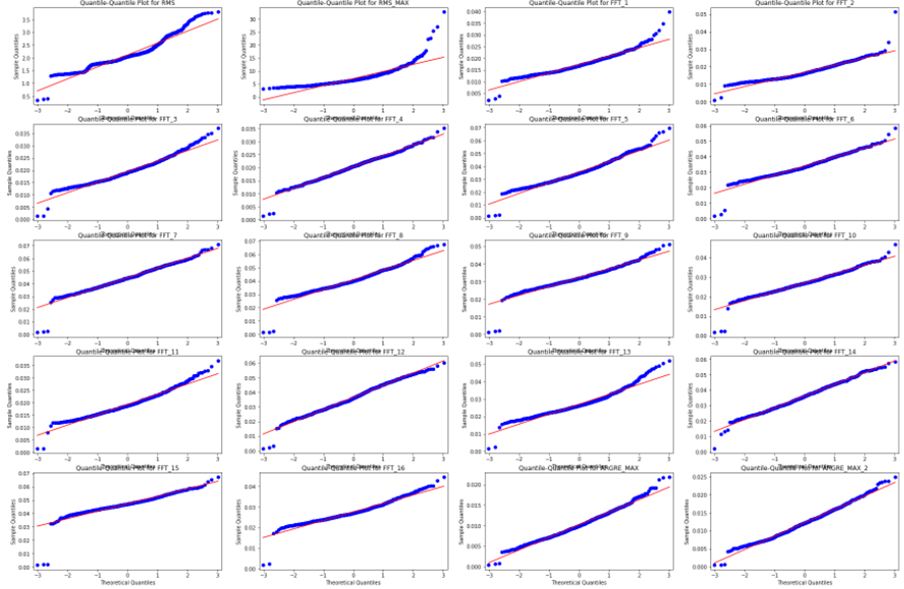
このまま一気にマハラノビス距離を算出してもいいのですが、まずはMT法の前提となる各特徴量の分布が正規分布に近いのかを検証したいと思います。分布が正規分布にどれくらい近いかはいくつかの検定法がありますが、正規分布と対象分布の分位点をプロットしたQQプロットが分かりやすいと思います。対象分布が正規分布になっていればQQプロットは直線を描きますが、いくつかの特徴量は両端(裾)部分が正規分布から乖離してしまっていることが分かります。
いくつかの分布を詳しく見てみましょう。分布が左右対称ではなく右方向に偏っています。
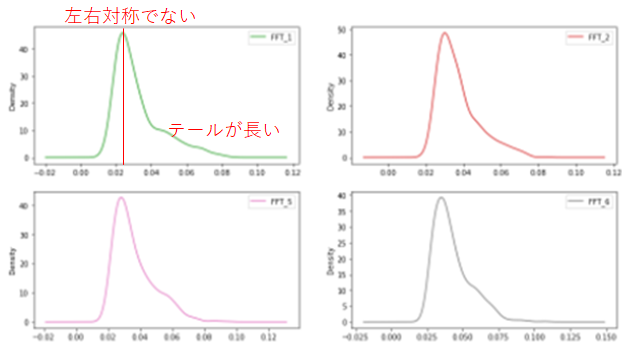
実はこの傾向は特徴量の分布としてはよく見られます。考えられる原因は、
i. 異常データが混ざっている
ii. 機械の運転状況(負荷など)が異なるデータが混ざっている
iii.センサ異常などのデータが混ざっている
などです。実際、右にずれた点の元データを確認し原因を考えます。iであれば”宝”を手に入れられるのでラッキーです。丁重に分離して検証に取っておけます。ii,iiiの場合は特徴量に閾値を設けて当該データを抜いてしまうか、2つの特徴量を組み合わせて補正できるかなど考えますがうまくいかないケースが多いです。今回もパーシバルの定理
https://ja.wikipedia.org/wiki/%E3%83%91%E3%83%BC%E3%82%BB%E3%83%90%E3%83%AB%E3%81%AE%E5%AE%9A%E7%90%86
を根拠ににRMS平均値ででFFTの値を補正することを試しましたが全くうまくいきませんでした。ただ、停止時と思われるデータが混入していたので、RMS値で足切りしました。
機械学習的な裏技もあります。正規分布から大きく乖離した特徴量にPower Transform(べき乗変換)を適用します。今回のようなロングテール型分布はBox-Coxや対数変換で長い尻尾を短くできます。ただMT法の本質に立ち返ると、安定稼働している機械の正常データの集合であれば、特徴量のブレは測定誤差に起因するもののはずで正規分布に近くなるはずです。従って正規分布にならない原因を探る方が正しいアプローチだと思います。特に、コブが2つになるような分布が現れるようであれば、それぞれのコブに該当する原因をさぐり、別クラスタとしてデータを分割すべきでしょう。
マハラノビス距離の計算
MT法のミソは、各特徴量のデータ分布が正規分布であれば算出されるマハラノビス距離の分布がカイ2乗分布に従うという点です。カイ2乗分布は既知の分布ですので、計測した値のマハラノビス距離が例えば"正常クラスタの99.9%に入ってない”というような定量的な判断ができます。まあ今回のように正規分布から乖離する特徴量がある場合は、結果的にどこまでカイ2乗分布に乗るか怪しいですが、まずはマハラノビス距離を計算してみましょう。マハラノビス距離(厳密にはマハラノビス距離の2乗, D^2と表記します)
D^{2} = ( x - \mu)^{T}\Sigma^{-1}(x-\mu)\\
xは特徴量を縦に並べたベクトル、μはその平均値を並べたベクトルで、今回は特徴量20個ですから20x1ベクトルになります。Σは共分散行列とよばれ、以下のように算出します。今回は20x20行列になります。
\Sigma = \frac{1}{N}(x-\mu)^{T}(x-\mu)
python, numpyであればの以下のように数行で書けます。
import numpy as np
def mahalanobis(x):
# calculate mu and E
mu = x.mean(axis=0)
mu_x = x - mu
assert mu_x.shape == x.shape
# calculate covariance matrix
cov = np.cov(x.values.T)
inv_conv = np.linalg.inv(cov)
# mahalanobis
dist_m = np.dot(np.dot(mu_x, inv_conv), mu_x.T)
return dist_m.diagonal()
それでは計算結果を見てみましょう。
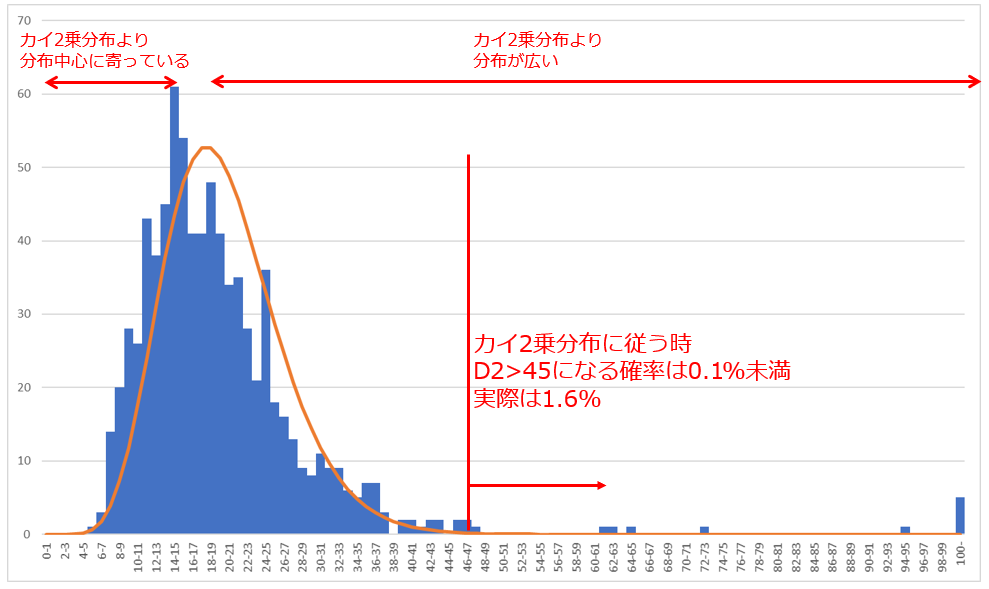
ヒストグラムは今回のデータのマハラノビス距離D^2の分布、オレンジのカーブは本来であれば追従するはずの自由度20のカイ2乗分布です。一部の特徴量の分布が正規分布から乖離していた割にはよくフィットしていると思います。特徴としては、
i. クラスタ中心に寄っている点がより多い
ii.理論値より多くの外れ値が存在する
と言えます。例えばマハラノビス距離が45以上は理論的には全体の0.1%のはずですが、実際は1.6%の測定点が45以上になっています。100を超えるものも5つもあります(理論値は0個)。実はこれらの元データを見てみるとセンサノイズと思われる振り切った加速度値が混ざったものなどが確認できました。
終わりに
今回は機械学習というより伝統的な多変量解析による品質管理手法であるMT法を試しました。後稿で紹介予定のオートエンコーダーなどの手法に比べると古臭さはありますが、現場ではまだまだ現役で有用なツールだと思います。今回は実際異常データがないのでパーセンタイルで0.1%あたりに閾値を設けてしばらくデータ収集を続けることになります。上記の結果から誤検出(false positive)も一定の割合で発生するでしょうが、機械学習現場の現実として(特にモデル設計初期は)誤報はある程度我慢する必要があります。もちろん異常を見逃すようであればアプローチを根本的に見直す必要がありますが。
(文責・お問合せ先: ハーティング株式会社 能方研爾 kenji.nogata@harting.com)